基于Chirp_z变换与方位变标地球同步轨道SAR成像算法

李财品 何明一

1 引言

地球同步轨道合成孔径雷达（GEosynchronous Orbit SAR, GEO SAR）具有重访周期短，观测范围广，可实现对特定区域长时间驻留观测等优点，目前已经成为研究热点。地球同步轨道SAR具有区别于低轨SAR特性，相关文献对同步轨道SAR的成像机理[1,2]，成像算法[39]-，系统设计[10,11]等开展研究，尤其是成像算法，更是研究的热点。

与低轨合成孔径雷达（SAR）的成像算法相比较，GEO SAR成像处理更加复杂。主要表现为停-走-停回波假设不成立，非直线运动，大成像场景距离空变，长合成孔径时间内方位时变，地球自转影响大造成了距离与方位耦合严重等。文献[3]针对“停-走-停”回波假设不成立的问题，分析了“停-走-停”回波模式带来的误差并在成像算法中进行了补偿。文献[4-6]针对非直线运动弯曲轨迹成像的问题，使用高阶逼近建立了曲线轨迹模型下的斜距方程，并结合级数反演法，推导了回波信号2维频谱高阶近似表达式，然后在此基础上提出了改进频域成像算法。针对距离方位耦合严重，距离空变性、方位时变性强的问题，文献[5-9]分别提出了采用改进的CS算法，改进的NLCS算法，改进RD算法，子孔径处理方法，时域卷积算法等多种方法来解决。然而上述各种频域算法不同程度上存在距离向处理复杂或者对信号方位时变性重视不足的问题，而时域算法（如时域卷积算法等）存在计算效率低下，实际中较少使用。

本文提出了一种基于Chirp_z变换与方位变标新的GEO SAR成像算法，考虑了“停-走-停”回波假设带来的相位误差，利用高效的Chirp_z变换校正距离走动，简化距离向成像处理，利用改进的变标因子校正方位向信号一次，二次，三次展开项系数的线性时变性，并且补偿了变标操作引入的相位误差。本文的组织结构如下：第2节对GEOSAR的回波模型进行了研究，考虑“停-走-停”假设带来的误差；第3节详细推导了算法整个过程，给出了算法流程图；第4节首先对算法中的假设条件及约束条件进行仿真分析，然后根据轨道参数对成像场景不同位置的点目标进行了成像仿真，并评估了成像效果；第5节对本文进行了总结。

2 回波模型

假设雷达发射线性调频信号，回波经过解调后的信号模型可以表示为

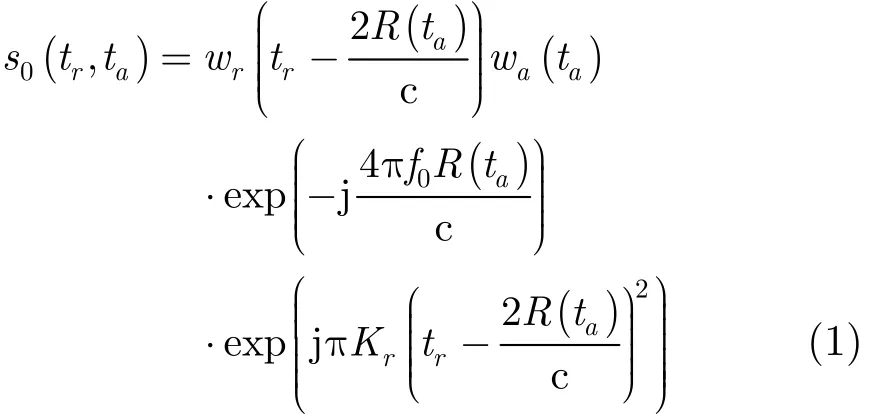
其中，tr为距离向时间，ta为方位向时间， wr为距离向包络， wa为方位向包络， f0为雷达中心频率，Kr为距离向信号调频率，c为光速，R （ ta）为目标点到卫星瞬时斜距。

GEO SAR回波时延长达200～300 ms量级，常规低轨及机载SAR的信号回波“停-走-停”模式不再适用于GEO SAR。根据文献[3]，“停-走-停”假设带来的距离误差为

其中， RS, RT分别为卫星位置与目标点位置矢量；VS, VT分别为卫星位置与目标点位置矢量一阶导数。

通过补偿“停-走-停”假设带来的误差后可将斜距表达式直接写成常规的表达方式。将其进行泰勒级数展开并表示成标量形式[12]，根据仿真分析四阶展开能够满足精度要求，则

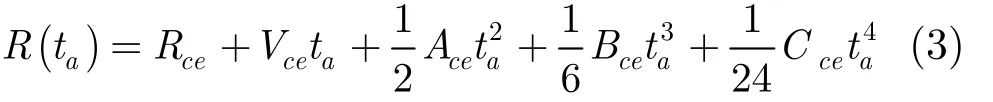
其中， Rce表示为波束中心时刻斜距，Vce, Ace, Bce,Cce分别表示为斜距一阶、二阶、三阶和四阶导数。

3 成像算法

对原始回波信号进行距离向傅里叶变换，可写成：

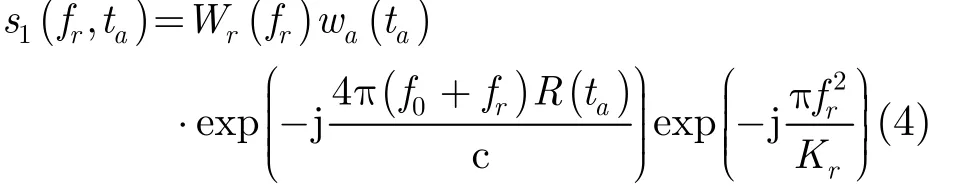
其中，rf为距离向频率。

首先补偿“停-走-停”假设带来的误差，补偿因子为

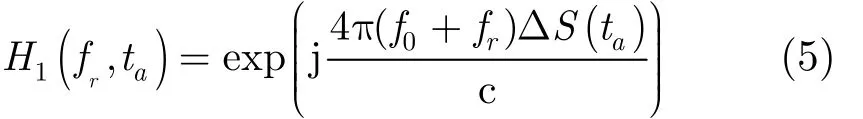
通过补偿后，将 R （ ta） 表达式代入式（4）并进行方位向傅里叶变换，利用驻定相位原理及级数反演原理进行求解，可得到2维频域信号表达式[12]：

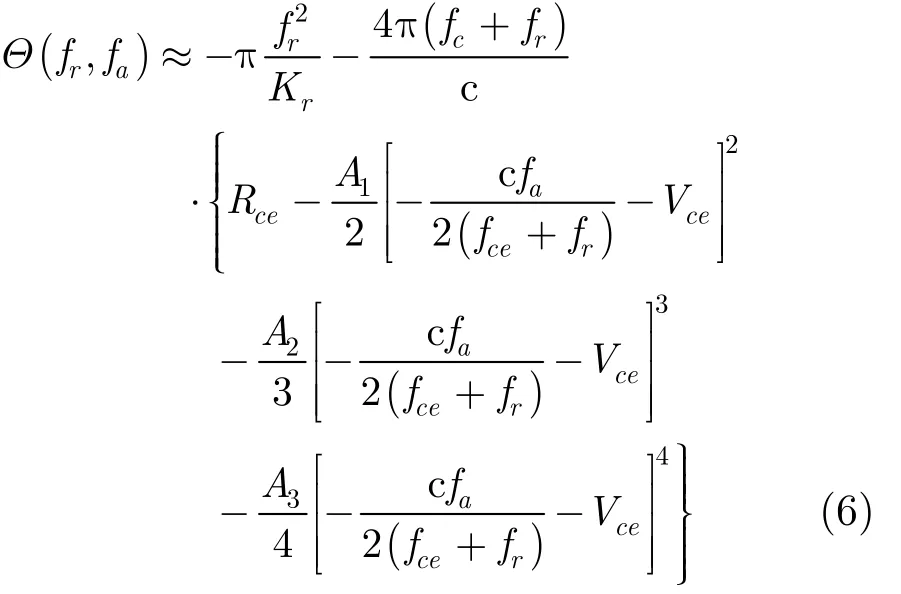
其中， fa为方位向频率，并且 A1= 1 /Ace, A2=-, A = （- A）/6A5。3ce

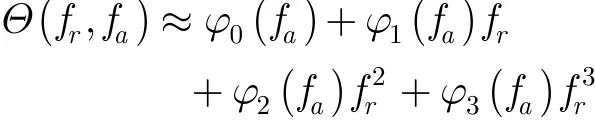
其中， φ0（fa）与距离频域 fr无关，为方位调制信号项。 φ1（ fa） 与距离频域 fr一次项有关，代表目标距离徙动项，φ2（fa）与距离频域 fr二次项有关，φ3（fa）与距离频域 fr三次项有关。 φ1（fa）, φ2（fa）, φ3（fa）表达式可参见文献[12]。而 φ0（fa） 由于涉及后继公式推导，这里给出表达式：

其中 fd=- 2Vce/λ。

在一定的成像范围内，忽略二次，三次耦合项的距离空变性，对应的二次距离压缩与三次压缩函数为

经过上面的补偿项相乘以后，回波信号可写为

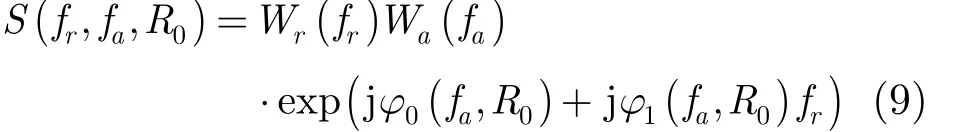
其中 R0代表场景内任意目标点距离。将距离频域 fr一次项分解成与场景参考距离有关与距离变化量有关的两个部分[13]。假设任意距离与参考距离变化量为ΔR，则ΔR = R0- Rref。利用补偿因子 H3（fr,fa, Rref）补偿参考距离处的一阶距离项：

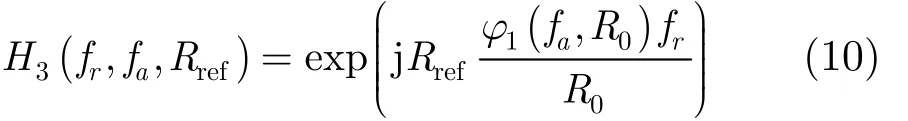
而与变化量为RΔ有关的一阶距离项可分解为

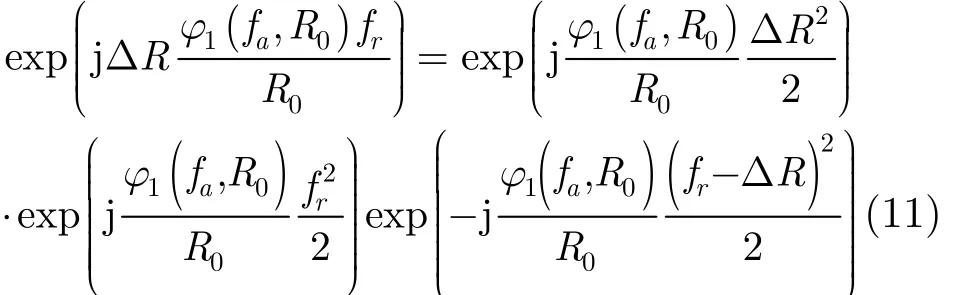
再将回波信号进行距离向逆傅里叶变换：

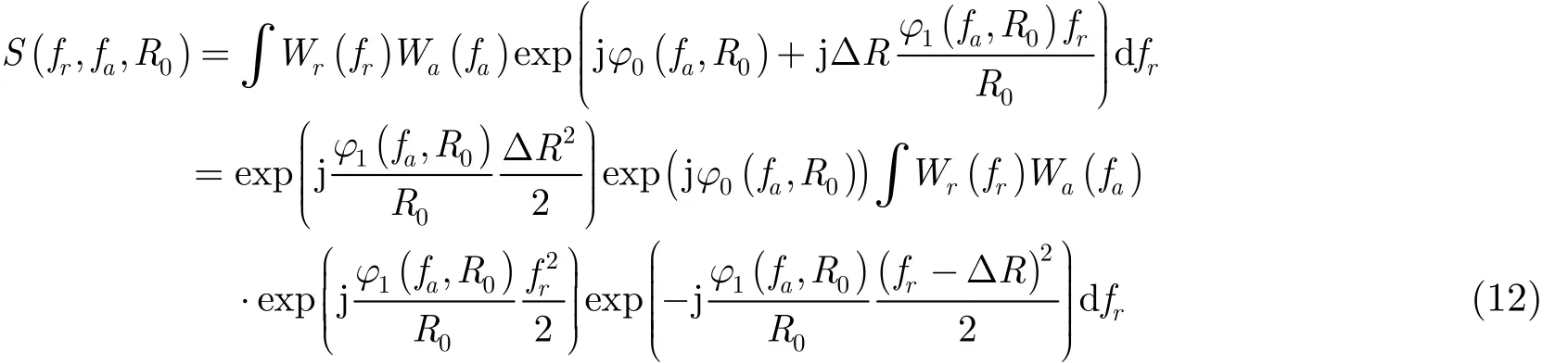
可以看出，上述过程其实就是Chirp_z变换。经过Chirp_z变换，回波信号为距离时域方位多普勒域，将回波方位向信号变换到时域，经过方位向IFFT变换后可得到：

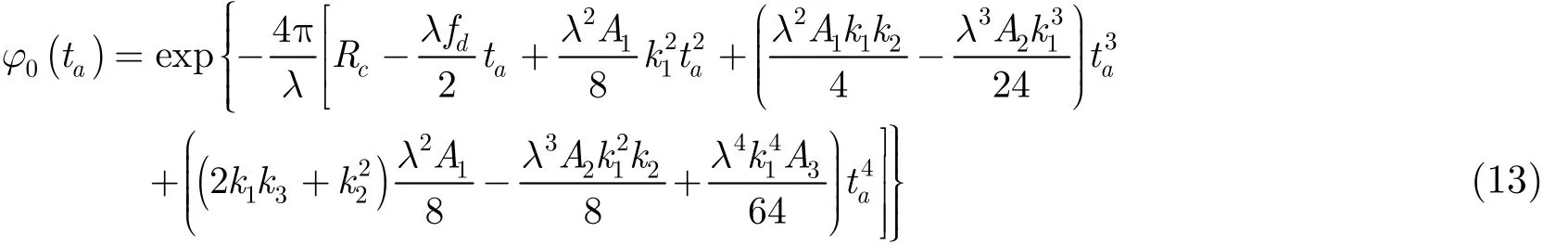
根据仿真分析，在一定时间范围内，方位信号展开式中的一次项，二次项，三次项系数时变性主要表现为线性变化。假设展开式一次项，二次项，三次项系数变化率分别为 Δ M , Δ M1, ΔM2，并将方位向信号表示为与波束中心位置tce相关表达式，则信号方位时变性可以表示为

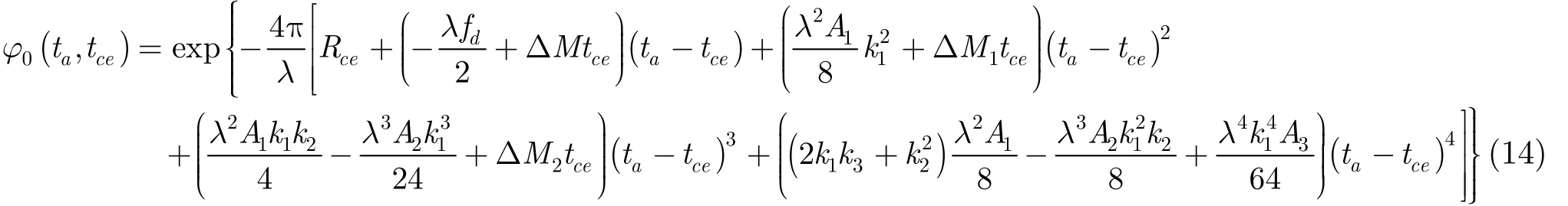
对于宽测绘带场景，方位向展开项系数也会随着距离向变化，可以采用沿距离门更新系数的方法来处理。

在方位时域利用改进的变标因子进行方位信号时变补偿，变标因子可表示为

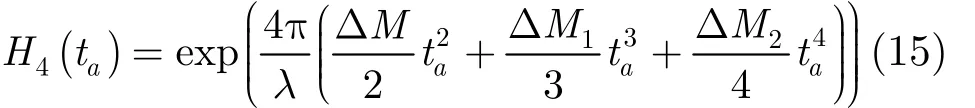
令ta- tce= t1，经过时域内与改进的方位变标因子相乘后回波信号可表示为

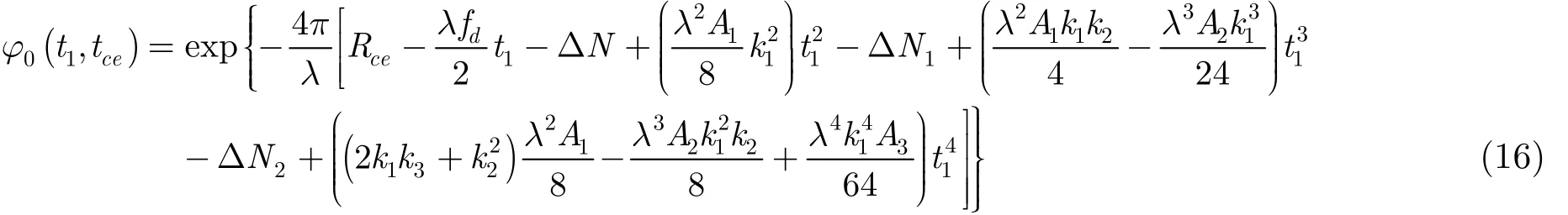
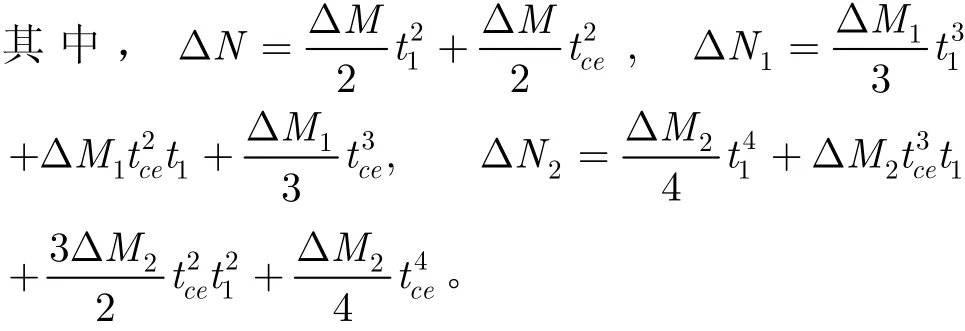
由方位向变标引入的相位 Δ N , Δ N1, Δ N2包含t1的一次项、二次项及更高阶项可以通过在频域内进一步的补偿来消除。

方位向时变性补偿后进行方位FFT变换，在方位频域进行方位向压缩及变标操作相位误差补偿，相乘的函数为

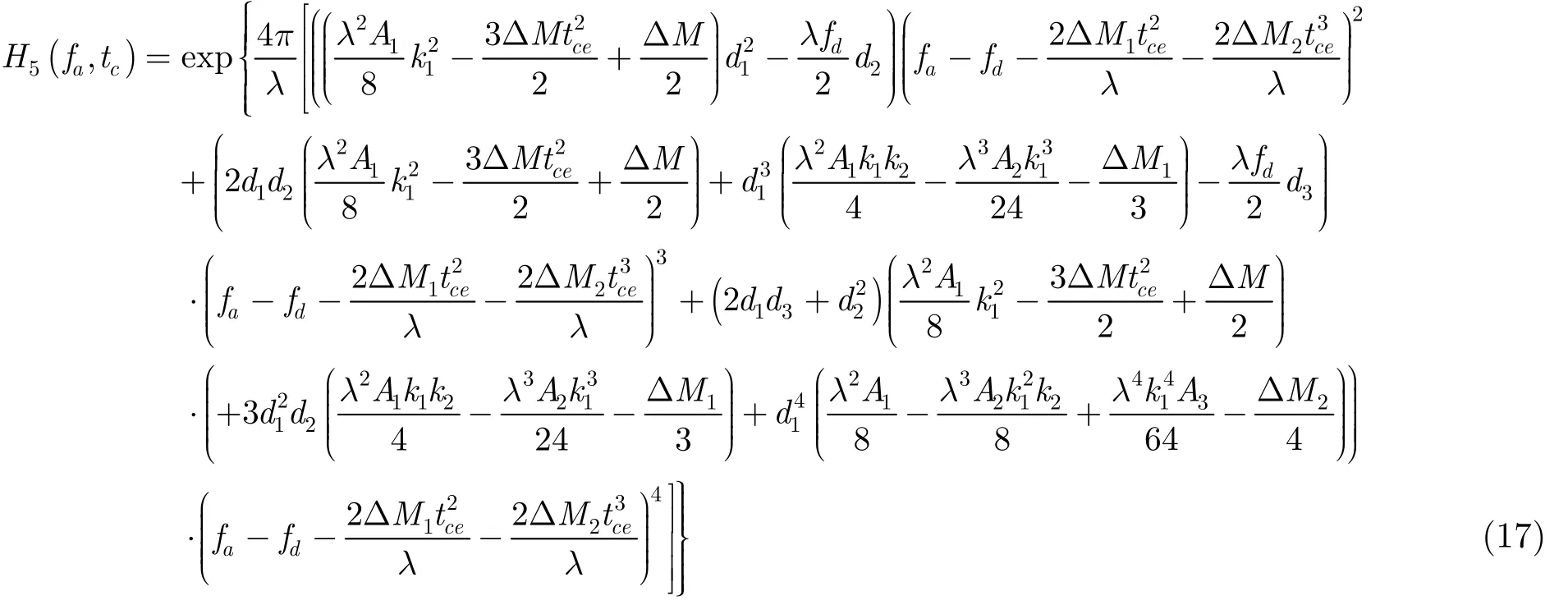
其中

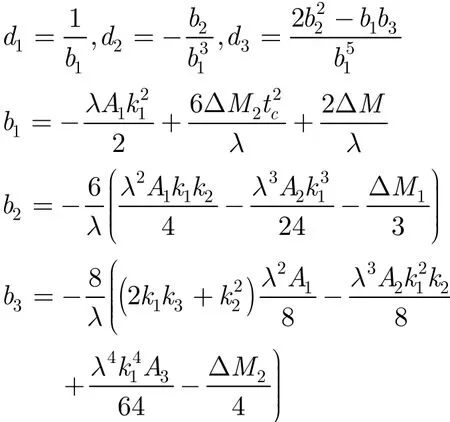
表1 仿真参数

最后进行方位向IFFT变换，得到2维图像。

整个算法的流程如图1所示：

4 仿真实验

4.1 约束条件分析

对算法约束条件及点阵目标进行仿真分析，其中仿真参数如表1所示。

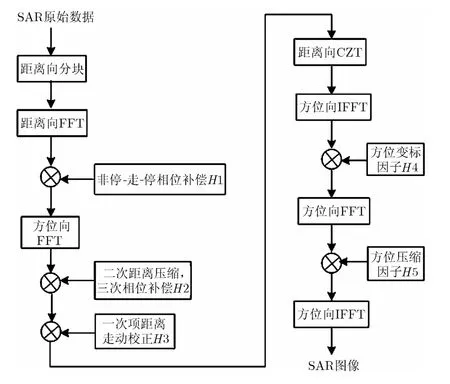
图1 本文算法流程

（1）距离向分块分析 距离向利用 CZT 变换进行处理时，在一定的成像范围内忽略二次，三次耦合项的距离空变性，则带来的误差为

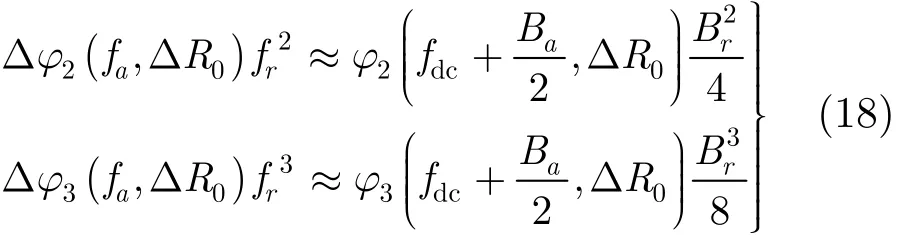
其中 fdc为多普勒中心频率， Ba为方位多普勒带宽，Br为发射信号带宽。

耦合项二次项，三次项随斜距变化误差示于图2。在一定的成像场景及成像分辨率情况下，若＜45°, Δ φ ＜ 4 5°，则可以忽略二次，三次耦3合项的距离空变性。通过仿真分析，在本文仿真参数下，满足该条件的成像场景大约为60 km。

（2）方位向信号多次项展开时变分析 为了证明方位向展开式一次项，二次项，三次项系数方位时变性主要表现为一次的变化，对展开式系数随时间变化进行分析。

通过图3的仿真分析表明方位向展开式中的一次项，二次项，三次项系数在一定时间范围内时变性主要表现为线性变化。

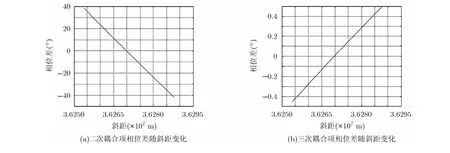
图2 耦合项二次项，三次项随斜距变化误差

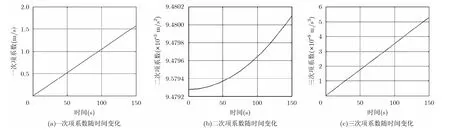
图3 展开式一次项、二次项，三次项系数方位时变性

4.2 点阵目标成像仿真

假设成像场景共有9个目标，分布如图4所示。

利用本文算法进行成像仿真分析，场景中心点目标，场景边缘点目标的仿真效果如图5所示。

对成像结果进行插值，无加窗处理，并对成像的点目标进行评估，成像性能指标如表2所示。

从成像结果及性能评估表可以看出，无论是场景中心点目标，场景边缘点目标都实现了良好聚集，峰值旁瓣比的指标接近理想值，能够满足成像需求。由于目标点4与目标点5正侧视成像，距离向与方位向旁瓣正交。而对于目标点 7，由于工作在非正侧视情况下，因此距离向与方位向旁瓣非严格正交，但也实现了良好的聚焦成像。

高效处理与方位信号一次，二次，三次展开项的线性时变性补偿及变标操作引入的相位误差补偿，详细推导了算法的表达式。成像及性能评估结果表明该算法可实现地球同步轨道 SAR一定成像幅宽及轨道时间段成像聚焦。

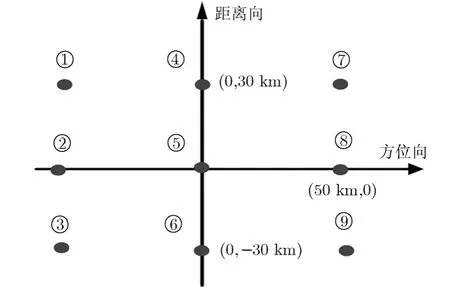
图4 点目标分布示意图

5 结束语

本文提出了一种基于Chirp_z变换与方位变标的地球同步轨道SAR成像算法，实现了距离向成像

表2 成像性能评估

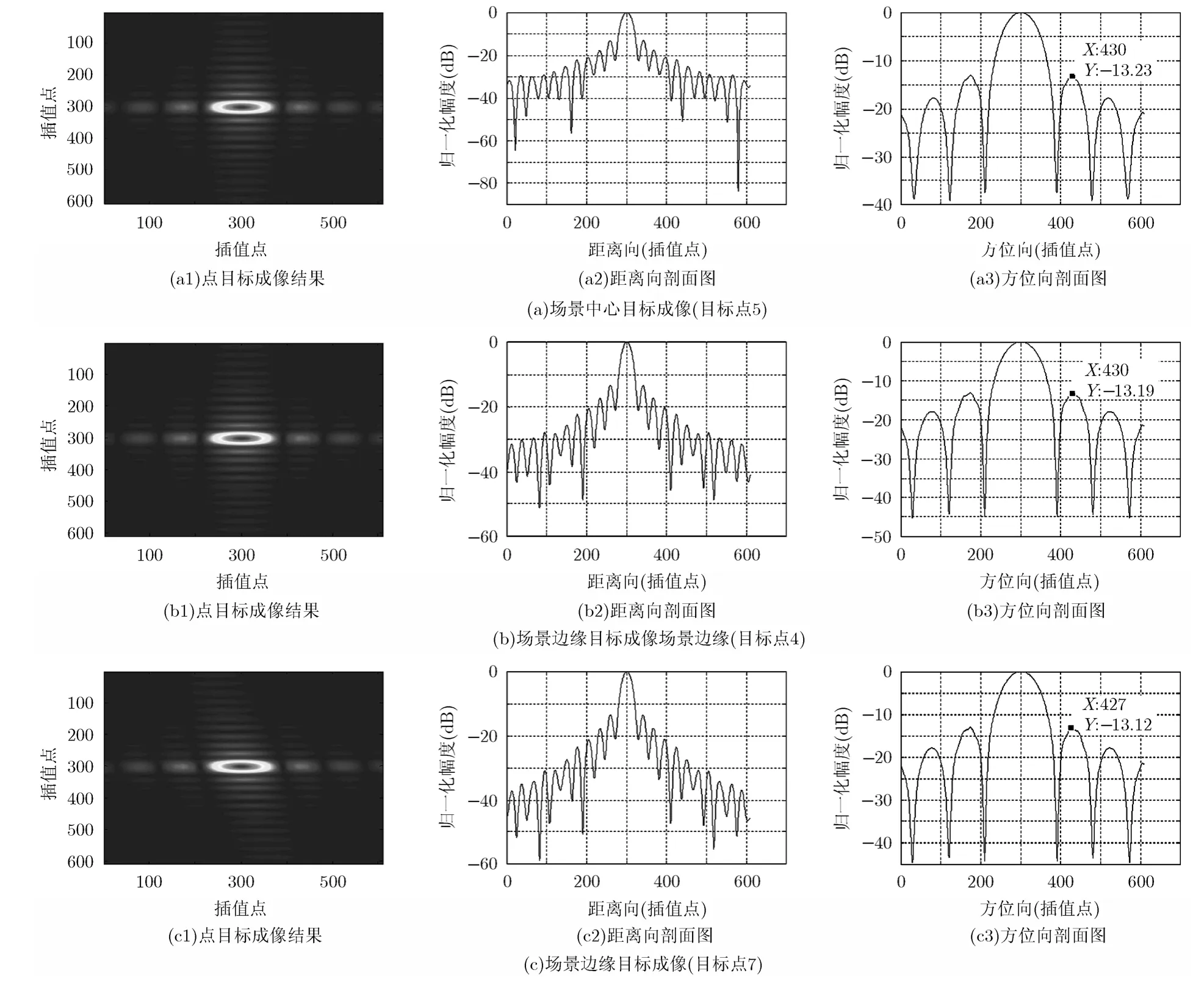
图5 点目标成像仿真

[1] Wu Zhou-ting, Huang Li-jia, Hu Dong-hui,et al.. Azimuth resolution analysis in geosynchronous SAR with azimuth variance property[J]. Electronics Letters, 2014, 50（6）:464-466

[2] Hobbs S E, Snapir B, Corstanje R, et al.. Simulation of geosynchronous radar and atmospheric phase compensation constraints[C]. Proceedings of the IET International Radar Conference, Xi’an, China, 2013: 1-6.

[3] Hu Cheng, Long Teng, Liu Zhi-peng, et al.. An improved frequency domain focusing method in geosynchronous SAR[J].IEEE Transactions on Geoscience and Remote Sensing, 2014,52（9）: 5514-5528.

[4] Zhao Bing-ji, Qi Xiang-yang, Song Hong-jun, et al.. An accurate range model based on the fourth-order doppler parameters for geosynchronous SAR[J]. IEEE Transactions on Geoscience and Remote Sensing Letters, 2014, 11（1）:205-209.

[5] Bao Min and Xing Meng-dao. Chirp scaling algorithm for GEO SAR based on fourth-order range equation[J].Electronics Letters, 2012, 48（1）: 56-57.

[6] Hu Cheng, Liu Zhi-peng, and Long Teng. An improved CS algorithm based on the curved trajectory in geosynchronous SAR[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2012, 5（3）: 795-808.

[7] Wu Xiu, Zhang Shun-sheng, Li Jing. et al.. Geosynchronous SAR image formation based on advanced hyperbolic range equation[C]. Proceedings of IEEE Geoscience and Remote Sensing Symposium （IGARSS）, Munich, Germany, 2012:4042-4045.

[8] Sun Guang-cai, Xing Meng-dao, Wang Yong, et al.. A 2-D space-variant chirp scaling algorithm based on the RCM equalization and subband synthesis to process geosynchronous SAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52（8）: 4868-4880.

[9] Li Zhuo, Li Chun-sheng, Yu Ze, et al.. Back projection algorithm for high resolution GEO-SAR image formation[C].Proceedings of IEEE Geoscience and Remote Sensing Symposium （IGARSS）, Vancouver, Canada, 2011: 336-339.

[10] Hobbs S, Mitchell C, Forte B, et al.. System design for geosynchronous synthetic aperture radar missions[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014,52（12）: 7750-7763.

[11] Ruiz-Rodon J, Broquetas A, Makhoul E, et al.. Nearly zero inclination geosynchronous SAR mission analysis with long integration time for earth observation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52（10）: 6379-6391.

[12] 黄丽佳, 胡东辉, 丁赤飚. 中高轨道 SAR 信号建模和成像方法研究[J]. 国外电子测量技术, 2011, 30（6）: 21-27.Huang Li-jia, Hu Dong-hui, and Ding Chi-biao. Study on signal modeling and imaging approach for mediumearth-orbit SAR[J]. Foreign Electronic Measurement Technology, 2011, 30（6）: 21-27.

[13] 周鹏, 周松, 熊涛等. 基于级数反演的弹载SAR下降段CZT成像算法[J]. 电子与信息学报, 2010, 32（12）: 2861-2867.Zhou Peng, Zhou Song, Xiong Tao, et al.. A chirp-z transform imaging algorithm for missile-borne SAR with diving maneuver based on the method of series reversion[J]. Journal of Electronics & Information Technology, 2010, 32（12）:2861-2867.