干扰背景下基于双圆阵的全向测角方法

田 超 文树梁

1 引言

在现代战争中，如何在复杂的干扰环境下有效探测目标是雷达研制面临的严峻挑战。特别是对于文献[1]中提到的移动式、小尺寸方位全向米波雷达，该雷达虽然因为具有反隐身和反辐射导弹的能力以及机动性强、系统组成简单、成本低且可进行空域全方位的同时覆盖等特点而逐渐受到关注，但其方位全向的特性亦使得其更容易受到压制干扰的影响。

由于该米波雷达的发射、接收方向图均是方位全向的，因而通过降低方向图旁瓣以及常规旁瓣相消[2,3]的抗干扰方法难以有效应用；而且该雷达的测角体制与常规警戒搜索雷达不同，是利用均匀圆阵相位模式空间中的-1，0和1阶模式进行联合测角，故无法使用类似于文献[4]中结合和差波束与辅助波束的新方法达到抗干扰的目的。另外，方位全向米波雷达的阵列口径小，阵元间互耦严重，而在互耦系数未知的情况下，诸如自适应置零方法[5,6]、自适应干扰对消方法[7]和基于阻塞预处理的抗干扰方法[8,9]的应用均受到限制。相比之下，文献[10]基于JADE的盲源分离方法和文献[11]基于典范相关分析的盲源分离方法可以有效实现干扰和目标回波的分离，但用于全向测角的相位信息全部在分离矩阵中，因此无法利用盲源分离后的输出信号得到目标方位的估计。文献[12]利用噪声调频信号的恒模特性重构出干扰进而在时域实现干扰对消的方法，针对噪声调频干扰的效果较好，但当干扰兼具调频和调幅特性时，干扰重构误差较大。利用干扰和目标回波的极化差异可以实现有效的干扰抑制[13,14]，文献[15]提出的自适应极化对消滤波器和文献[16]提出的雷达收发极化的联合优化方法可用于方位全向米波雷达，但前者在干扰与目标回波极化特性接近以及干扰与目标方位夹角较小时，对消损失较大，而后者基于现有方位全向雷达的系统组成则不易实现。

由于米波全向雷达阵列口径较小，阵元间互耦效应严重，这限制诸多经典测角方法和抗干扰方法的应用。相对于干涉测角、和差单脉冲测角以及0阶和1阶相位模式测角等方法，文献[1]提出的一种实现简单的联合测角方法，其利用-1阶和1阶相位模式消除互耦的影响，利用-1阶和0阶相位模式消除测角模糊，进而获得目标方位的无模糊估计。在该方法的基础上，可以进一步得到基于-1阶、0阶和1阶相位模式的干扰对消和对消后目标方位角估计方法，该方法实现简单且在不同压制干扰下均有效，但当干扰与目标方位夹角较小时，目标回波损失较大。为解决该问题，本文提出了基于大小双圆阵的干扰对消和目标方位估计方法，并对相位模式阶数和阵列参数的选择进行了分析，最后对所提方法的有效性进行了仿真验证。

2 基于高阶相位模式激励的干扰对消方法

均匀离散圆阵的天线阵元分布如图1所示，N个相同的天线均匀分布在直径为d的圆周上。

假设目标的方位角和俯仰角分别为θs和φs，干扰的方位角和俯仰角分别为θI和φI，阵列中心收到的目标回波和干扰信号分别记为sT（t）和I（ t） ，第k个阵元对应的接收支路中的噪声记为 nk（ t），均值为0，方差为 σ2。经过时域采样，sT（t），I（ t）和nk（ t） 分别对应输出sT（n），I（ n）和nk（ n）。经过匹配滤波后，若 n0为输出峰值对应的位置，此时信号、干扰和噪声分别对应的输出为sc（ n0） ，Ic（ n0） 和nck（n0） ，那么第k个阵元收到的信号经时域采样和匹配滤波后的输出可表示为

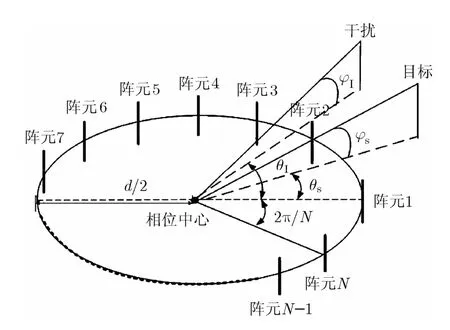
图1 均匀离散圆阵示意图

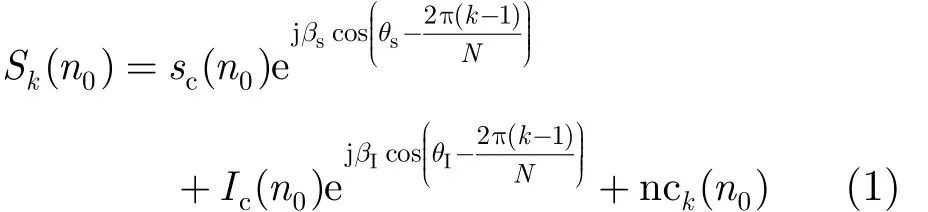
若 | φs-φI|较小，则|cosφs-cosφI|更小，此时可认为, Jm（.）为m阶贝塞尔函数，故不妨记 β = βs= βI。

利用式（1）可得均匀圆阵激励出的p阶和q阶相位模式为

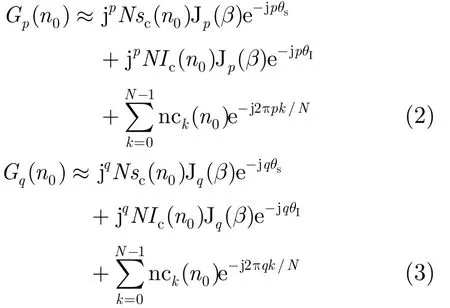
利 用pG 和qG-,qG 和pq≠）分别进行干扰对消可得

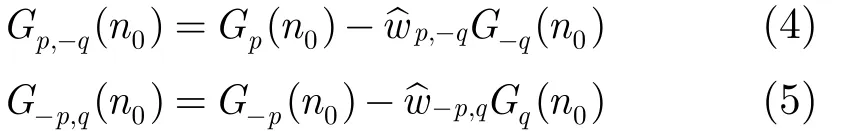
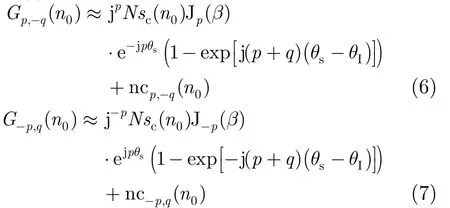
其中

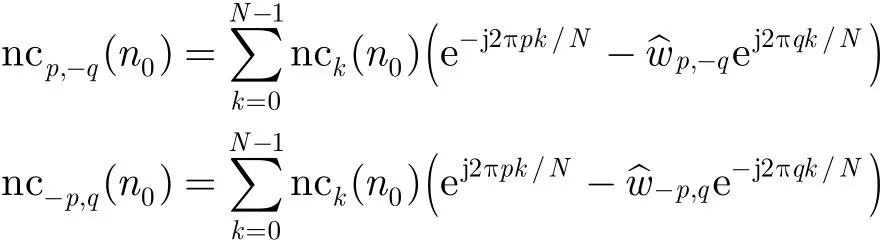
由式（6）和式（7）可知，干扰对消后目标回波的幅度为对消前的 Lp,q= | 2sin[（p + q ）（θs- θI）/2]|倍。在|θs-θI|较小时，Lp,q/L1,0随着p + q 的增大而增大，这意味着相比于利用0阶和-1阶模以及0阶和1阶模，利用p阶和 -q 阶模以及q和 - p 阶模来对消干扰（p + q ＞ 1 ），有利于减少目标回波的损失。

3 基于双圆阵的全向测角方法

若干扰对消后信噪比较高，则可由式（6）和式（7）得到

若（p - q ） θs-θI+ 2pδθI＜ π, δθI为干扰方位角的估计精度，则可得目标方位角的无模糊估计值

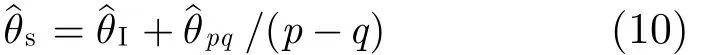
由式（10）知，目标方位角的估计精度取决于ˆθpq和ˆθI的精度以及p和q的取值。

ˆθI可通过-1, 0和1阶模进行无模糊测角获得。然而，采用-1, 0和1阶模进行无模糊测角对圆阵直径的要求往往与采用高阶相位模式对消干扰对圆阵直径的要求不一致，这种不一致将导致ˆθpq和ˆθI无法同时达到理想精度。以 p = 2 , q = 3 为例，为保证干扰对消后的信噪比从而使ˆθpq获得较高的估计精度，d宜取1.2λc，而为保证ˆθI的精度，d宜取0.45λc。若d取1.2λc，那么ˆθI的精度仅为d取0.45λc时的1/22，如果d取 0 .45λc，那么ˆθpq的精度仅为d取1.2λc的1/6，因此，为了使ˆθpq和ˆθI均获得较高的估计精度，可采用双圆阵。小圆阵可以布设于大圆阵中，两圆阵共圆心。

假设小圆阵的阵列直径为 d1，阵元数为 N1,β1= 2π d1cos φI/λc，小圆阵激励出的0, -1和1阶模分别记为 G '（ n）, G ' （n） 和G'（ n）。干扰方位角可

0-11在匹配滤波前利用多个快拍在最小均方误差的准则下估计得到，而利用大圆阵来估计目标方位角则需利用匹配滤波输出峰值点的相位信息。

若记利用小圆阵激励出的-1, 0和1阶模得到的干扰方位角ˆθI1，且有

由式（11）以及-1和0阶模得到的干扰方位角可以得到无模糊的I1θˆ，且其精度可表示为

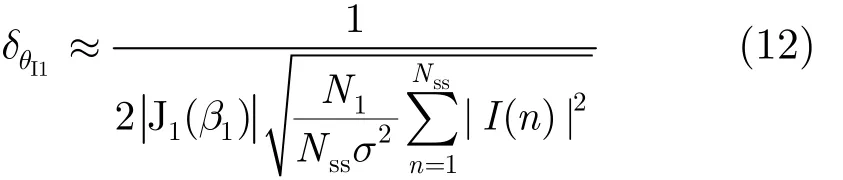
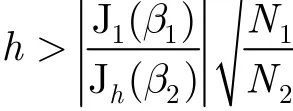
对消系数w︿p,-q和w︿-p,q则可利用 G-p（n）, Gp（n）,G-q（n） 和 Gq（ n） 计算得到。

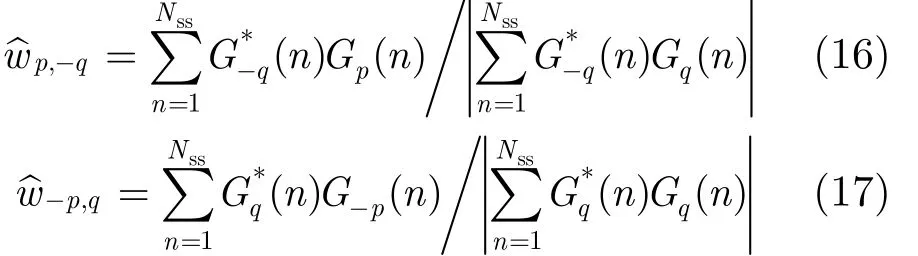
需要说明的是，米波全向雷达的阵列直径往往较小，阵元间的互耦较为严重。然而，在均匀离散圆阵的相位模式空间，互耦对各阶相位模式的影响等效于乘以一复系数，此点在文献[1]中有详细论述。由于该系数可包含在︿,pqw-和︿,pqw-中，故无需单独估计，也正是基于此，本文在建立数学模型时并未将互耦系数代入其中。

4 p,q,h及阵列参数的选择

出于对雷达高机动性以及铁路运输对装备尺寸的限制，阵列直径最好不超过3 m，而出于对隐身目标和反辐射导弹的探测需求，选用的发射频率为140～160 MHz，即要求阵列直～径最大不超过 1 .5λc，同时期望的仰角覆盖范围为0°45°。

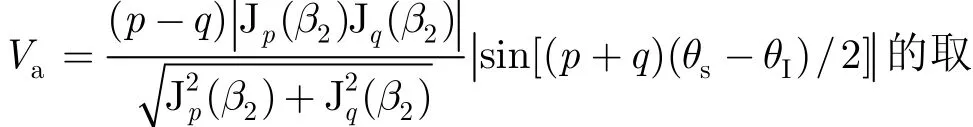
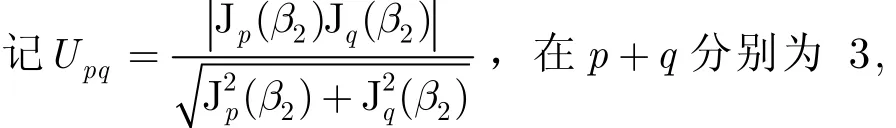
4, 5, 6, 7, 8时，在不同的p, q组合下， Upq随d / λccos φ的变化规律分别如图2～图7所示。

由图 2～图 7可得到，为保证Upq在0°～45°的仰角范围内均较大， p + q = 3 ,4,5,6,7,8时，p, q,d/λc的适宜取值分别为： p= 3 , q= 0 ,d/ λc= 0 .92; p = 3 , q = 1 , d / λc= 1 .06; p = 3 ,q= 2 , d / λc= 1 .35; p= 4 , q = 2 , d / λc= 1 .45;p= 4 , q= 3 , d/ λc= 1 .50; p= 5 , q= 3 ,d / λc= 1 .50。分别取上述6组参数时，在0°～45°的仰角范围内 Upq的最大值和最小值分别为：0.33和0.30; 0.23和0.18; 0.30和0.25; 0.22和0.18; 0.27和0.14; 0.19和0.05。

结合图2～图7以及图中分别对应的最佳 d /λc的取值，可以看出，随着p + q 的增大， d /λc的最佳取值逐渐增大，由于限制了d最大不超过 1 .50λc，因此p + q =7和8时的最优 d /λc只能取1.50。可以预见， p + q ＞ 8 并越来越大时， Upq的最大值和最小值越来越小，同时，从图6和图7可以看到，确定 d /λc后， Upq随着仰角增大迅速减小，因此适宜的p和q应在 p + q ≤ 6 时选取。

由于选择合适的p, q, d / λc的目的是为了使得 Vb尽量大，而在目标与干扰方位角较小时，p + q越大， Vb越大。考虑极端情况， | sin[2（θs-θI）]|,|sin[5（θs-θI）/2]|和|sin[3（θs- θI）]|分 别 为|sin[3（θs- θI）/2]|的4/3, 5/3和2倍，将相应的倍数等效到 p + q = 3 ,4,5,6时，各自最佳p, q, d /λc取值分别对应 Upq的最大值和最小值为0.33和0.30，0.30和0.24, 0.50和0.42, 0.44和0.36。通过比较不难发现， p = 3 , q = 2 , d / λc= 1 .35是更为合适的参数组合。

Vh的大小在存在干扰时影响干扰方位角的估计精度，在不存在干扰时直接影响目标方位角的估计精度，然而无论干扰存在与否，均希望 Vh尽量大。h取不同值时， Vh随 d / λccosφ的变化如图8所示。

由图8可知，d / λccos φ = 0 .95～1.35时，V3整体取值最大，因此h以取3为宜。

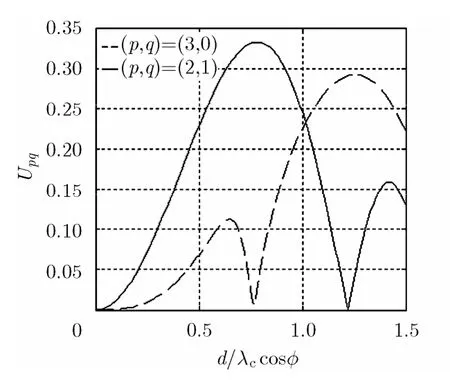
图2 p + q = 3 时 U pq随 d / λ c cosφ 的变化

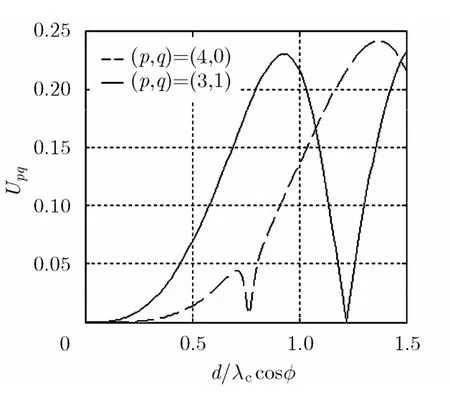
图3 p + q = 4 时 U pq随 d / λ c cosφ 的变化

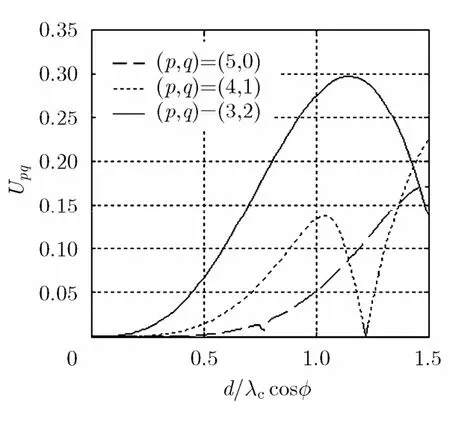
图4 p +q=5时Upq随 d / λ c cosφ 的变化

图5 p + q = 6 时 U p q随 d / λ c cosφ 的变化

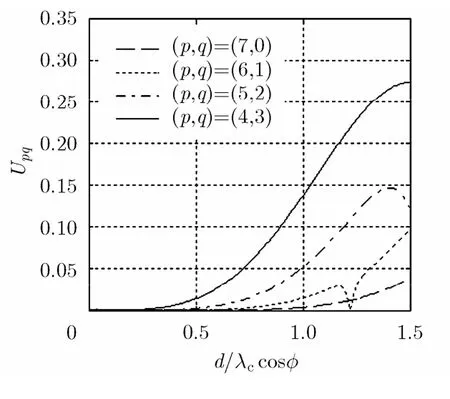
图6 p + q = 7 时 U p q随 d / λ c cos φ 的变化

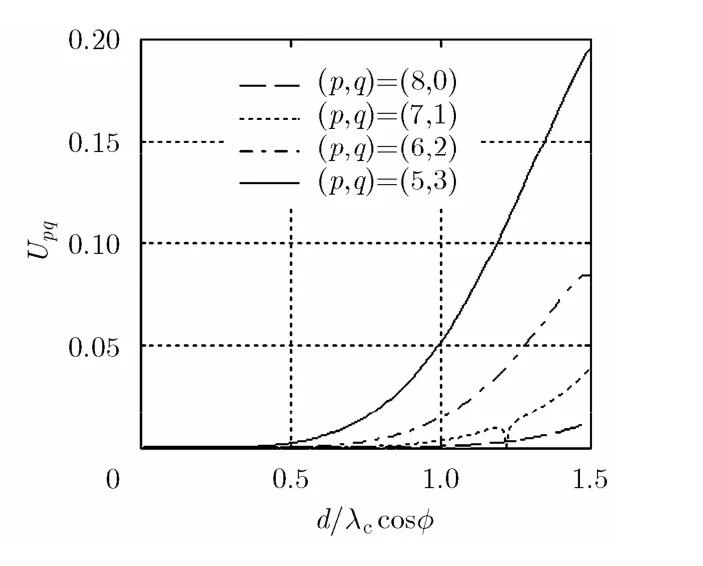
图7 p+q=8时Upq随 d / λ c cos φ 的变化

在确定阵列直径d为 1 .35λc以及测角中使用的最高阶相位模式为3阶后，可以确定所需的天线阵元数。天线阵元数的确定，以仰角为 0°且利用最高阶数测角时，方位最大固有误差不超过 1°为准则。由文献[1]知，固有误差在阵元数为偶数和奇数时存在差异。通过仿真计算可知，当阵元数为不小于10的偶数或者不小于9的奇数时，利用3阶和-3阶相位模式测角得最大固有误差小于1°。阵元数为偶数时，关于圆阵中心对称的两个阵元可共用一路接收机，可以简化系统，减少硬件成本，但这亦可能造成两个阵元在进入接收机之前引入的幅相不一致无法补偿；阵元数为奇数时，在相同的最大固有误差要求下，所需的阵元数更少，但接收机数量与阵元数应相同。因此，阵元数是奇数或偶数应根据实际需求选定。

综上所述，测角及大圆阵相关参数的选择为：p= 3 , q = 2 , h = 3 ，大圆阵 d / λc= 1 .35，阵元数为不小于10的偶数或者不小于9的奇数，小圆阵的阵列参数选择可参见文献[1]。

5 仿真结果及分析

干扰方位角为40°，单个阵元接收支路单脉冲信干比为-60 dB。小圆阵直径0.9 m，阵元数为8，大圆阵直径为2.7 m，阵元数为16。大圆阵利用3阶和-2阶，-3阶和2阶模对消干扰，利用3阶和-3阶模获得更高精度的干扰方位角。

由于压制干扰的类型不影响对消效果，故不妨假设干扰为射频噪声干扰。脉冲压缩前，单个阵元接收支路单脉冲信噪比分别为-10 dB和0 dB时，利用单圆阵和双圆阵进行干扰对消的效果对比分别如图9和图10所示，其中图9（a）和图10（a）为单圆阵-1阶模和0阶模对消后的脉冲压缩输出，图9（b）和图10（b）为双圆阵中利用大圆阵的-3阶模和2阶模对消后的脉冲压缩输出。

图 9中利用单圆阵和双圆阵进行干扰对消后的信干比分别为13.6 dB和20.47 dB，图10中利用单圆阵和双圆阵进行干扰对消后的信干比分别为17.2 dB和21.5 dB，这说明无论单圆阵还是双圆阵，干扰均被较好地对消掉。

由图9可以看到，单个阵元支路脉冲压缩前信噪比为-10 dB时，利用单圆阵对消后，从匹配滤波的输出中无法检测到目标，而利用双圆阵对消后的匹配滤波输出中可以检测到目标，且经过1000次蒙特卡洛仿真可以得到目标方位角估计值的均值为30.3°，均方根误差为9.9°。

本节主要验证本文所提方法相对于单圆阵利用-1, 0和1阶模进行干扰对消和目标方位估计方法，在减小目标回波损失以及提高目标方位角测角精度上的改进。

发射信号为线性调频信号，载频为150 MHz，带宽为5 MHz，脉宽为100 μs，脉冲重复间隔1 ms，时域采样率为5 MHz，静止目标距雷达51.029 km，目标和干扰的仰角均为10°，目标方位角为30°，

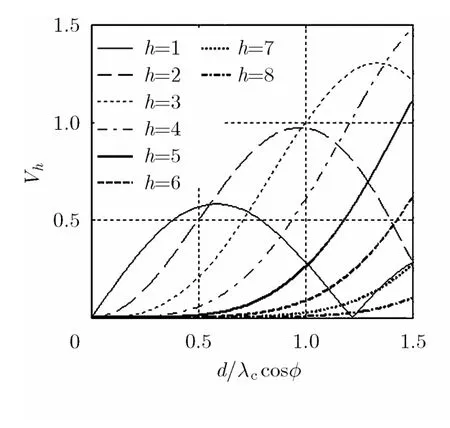
图8 不同的h取值时 Vh 随 d / λ c cos φ 的变化

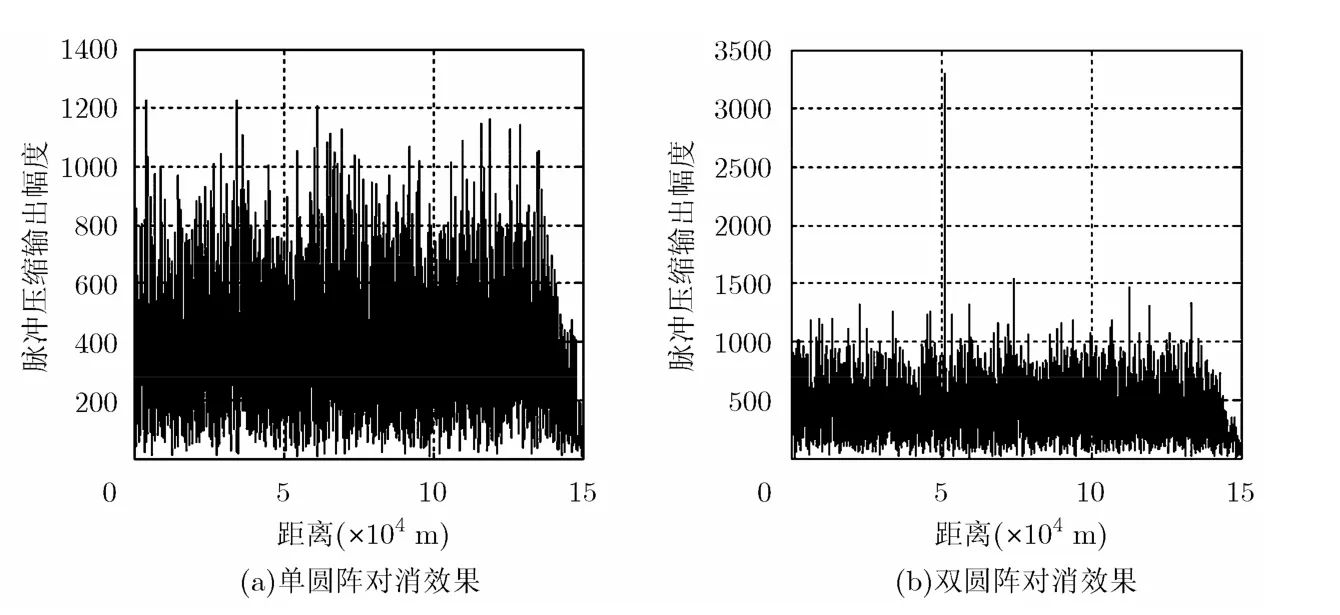
图9 射频噪声干扰且信噪比为-10 dB时单、双圆阵对消效果对比

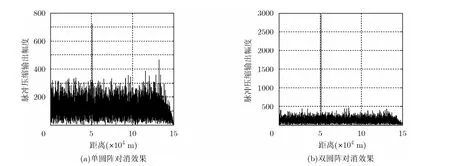
图10 射频噪声干扰且信噪比为0 dB时单、双圆阵对消效果对比

由图10可以看到，单个阵元支路脉冲压缩前信噪比为0 dB时，分别基于单圆阵和双圆阵进行对消后，从匹配滤波的输出中均可检测到目标，但前者的输出峰值信噪比明显低于后者。经过1000次蒙特卡洛仿真可以得到利用单圆阵对消干扰后得到目标方位角估计值的均值为30.2°，均方根误差为12.5°，利用双圆阵对消干扰后得到目标方位角估计值的均值为29.9°，均方根误差为2.9°。

综上所述，基于双圆阵的对消方法在目标干扰方位夹角较小时可以相对地减小目标回波的对消损失，提高干扰对消后的信噪比，从而增大目标检测概率和提高目标方位角的估计精度。

6 结束语

本文针对小尺寸方位全向米波雷达提出了一种基于大小双圆阵相位模式激励的干扰对消和目标方位估计算法，并给出了相位模式阶数和阵列参数的选择依据。在目标与干扰方位夹角较小时，该算法可有效减小目标回波的损失，提高干扰对消后的信噪比，从而提高目标检测概率与目标方位角的估计精度。不过本文算法无法解决多干扰问题，因此如何消除多个干扰的影响还有待进一步的研究。

[1] 田超, 文树梁. 米波圆阵雷达全向测角算法及其性能分析[J].系统工程与电子技术, 2013, 35（12）: 2507-2512.Tian Chao and Wen Shu-liang. Omni-directional angle measurement algorithm of meter-wave circular array radar and its performance analysis[J]. Systems Engineering and Electronics, 2013, 35（12）: 2507-2512.

[2] Zeng Guo-qi, Li Si-yin, Zhang Yan, et al.. Low side lobe pattern synthesis using projection method with genetic algorithm for truncated cone conformal phased arrays[J]. Journal of Systems Engineering and Electronics, 2014, 25（4）: 554-559.

[3] 吉波, 张科, 刘晓婧, 等. 基于自适应旁瓣相消的干扰源方位估计方法[J]. 系统工程与电子技术, 2014, 36（10）: 1913-1917.Ji Bo, Zhang Ke, Liu Xiao-jing, et al.. DOA estimation method for jamming based on adaptive sidelobe canceller[J].Systems Engineering and Electronics, 2014, 36（10）: 1913-1917.

[4] Li Rong-feng, Rao Can, Dai Ling-yin, et al.. Combining sum-difference and auxiliary beams for adaptive monopulse in jamming[J]. Journal of Systems Engineering and Electronics, 2013, 24（3）: 372-381.

[5] Higgins T and Webster T. Mitigating interference via spatial and spectral nulling[J]. IET Radar, Sonar & Navigation, 2014,8（2）: 84-93.

[6] Su Hong-tao, Liu Hong-wei, Shui Peng-lang, et al.. Adaptive beamforming for nonstationary HF interference cancellation in skywave over-the-horizon radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49（1）: 312-324.

[7] Tan D K P, Lesturgie M, Sun Hong-bo, et al.. Space-time interference analysis and suppression for airborne passive radar using transmissions of opportunity[J]. IET Radar,Sonar & Navigation, 2014, 8（2）: 142-152.

[8] 王强, 张永顺, 司文涛. 基于阻塞预处理的多基地雷达抗主瓣干扰算法[J]. 电子与信息学报, 2014, 36（3）: 734-738.Wang Qiang, Zhang Yong-shun, and Si Wen-tao. Main-lobe jamming suppression algorithm for multistatic radar based on block preconditioning[J]. Journal of Electronics &Information Technology, 2014, 36（3）: 734-738.

[9] 苏保伟, 王永良, 李荣锋, 等. 阻塞矩阵方法对消主瓣干扰[J].系统工程与电子技术, 2005, 27（11）: 1830-1832.Su Bao-wei, Wang Yong-liang, Li Rong-feng, et al.. Mainlobe interference cancelling method via block matrix[J]. Systems Engineering and Electronics, 2005, 27（11）: 1830-1832.

[10] 王建明, 伍光新, 周伟光. 盲源分离在雷达抗主瓣干扰中的应用研究[J]. 现代雷达, 2010, 32（10）: 46-49.Wang Jian-ming, Wu Guang-xin, and Zhou Wei-guang. A study on radar mainlobe jamming suppression based on blind source separation algorithm [J]. Modern Radar, 2010, 32（10）: 46-49.

[11] Bai Zhi-mao, Huang Gao-ming, and Yang Lu-xi. A radar anti-jamming technology based on canonical correlation analysis[C]. Proceedings of International Conference on Neural Networks and Brain, Beijing, China, 2005（1）: 9-12.

[12] Du Dong-ping and Tang-bin. Noise FM jamming suppression via logarithm transform[C]. Proceedings of International Conference on Communications, Circuits and Systems,Fujian, China, 2008: 957-959.

[13] Gherardelli M. Adaptive polarization suppression of intentional radar disturbance[J]. IEE Proceedings F: Radar and Signal Processing, 1990, 137（6）: 407-417.

[14] Dai Huan-yao, Wang Xue-song, Li Yong-zhen, et al..Main-lobe jamming suppression method of using spatial polarization characteristics of antennas[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012,48（3）: 2167-2179.

[15] Nathanson F E. Adaptive circular polarization[C].Proceedings of IEEE International Radar Conference,Arlington, USA, 1975: 221-225.

[16] 施龙飞, 王雪松, 肖顺平. 干扰背景下雷达最佳极化的分步估计方法[J]. 自然科学进展, 2005, 15（11）: 1324-1329.Shi Long-fei, Wang Xue-song, and Xiao Shun-ping. A stepwise estimation method of optimal polarization of radar with interference[J]. Progress in Natural Science, 2005, 15（11）: 1324-1329.