长江口潮位非一致性及对水文设计的影响研究

张 悦，李国芳

(河海大学 水文水资源学院， 南京 210098)

长江口潮位非一致性及对水文设计的影响研究

张 悦，李国芳

(河海大学 水文水资源学院， 南京 210098)

采用Mann-Kendall检验和Spearman秩次相关检验等非参数统计检验方法分析了1950—2009年长江镇江和江阴站潮位的变化趋势。分析结果表明：镇江站年最高、最低潮位均存在显著的抬升趋势，年平均潮位也呈现不明显的上升趋势；江阴站除年最高潮位存在明显抬升外，年平均和年最低潮位的变化趋势均不显著。利用滑动t检验、滑动秩和检验以及Pettitt检验法对潮位时间序列进行突变检测，3种突变检测结果基本一致：镇江站年最高和年平均潮位均在1979年发生最强突变，年最低潮位在1987年发生变异；江阴站年最高潮位亦在1979年发生突变，但年平均和年最低潮位均未发生显著变异。以上述2站的年最高潮位序列为例，初步分析了潮位非一致变化的原因，潮位的这种非一致变化增加了水文频率分析的难度，并降低了水文设计值的防洪标准。

年最高潮位；年最低潮位；年平均潮位；非一致性；水文设计

水文序列作为水文分析计算的基础，必须满足可靠性、代表性和一致性。然而近年来，随着全球气候变化和人类活动的影响，特别是大规模社会经济活动的持续增强，高密度水利工程群、城市群和大范围水土保持措施的建设，形成了复杂的人类活动影响链，改变了流域下垫面的产汇流规律和天然洪水的时空分配过程[1]，进而使水文序列不满足一致性条件，而呈现出阶段性特征。分析和研究水文序列的变异规律，对水文模拟和预报、水文设计中频率分析方法的选择、水库调度方案的确定以及防洪减灾对策的制订都具有重要意义。因此，本文以镇江和江阴站为例，探讨其年最高、年最低以及年平均潮位的变化趋势和变异特性，从多个角度分析造成这一现象的原因，并进一步研究对水文设计的影响，为长江感潮河段的水利工程设计及运行管理提供参考依据。

1 资料与方法

1.1 资料收集与处理

本文收集了长江江苏段镇江和江阴站1950—2009年共60 a的每日潮位资料，以及长江大通站相应时段的逐日平均流量资料。2站潮位资料均采用镇江吴淞基面。

1.2 研究方法

本文采用Mann-Kendall检验和Spearman秩次相关检验[2]对2站3种不同的年潮位序列进行趋势分析，利用滑动t检验、滑动秩和检验和Pettitt检验对其进行突变点检测。检测结果较为满意，并在很大程度上避免了单一判别方法的不足。

1.2.1 Mann-Kendall检验

Mann-Kendall法是一种非参数检验方法，现已广泛用于降水、径流和气温等要素的时间序列的趋势变化分析。该方法不需要样本服从一定的分布，适用于水文、气象等非正态分布的数据，计算简便[3]。具体计算方法如下[4-6]所述。

原假设为序列无趋势性变化。对于样本容量为n的时间序列Xt，构造如下统计量：

(1)

式中:n为样本长度；xj和xi分别为序列中的数值。

(2)

当n≥10时，统计量近似服从正态分布，其标准化后的量由下式计算：

(3)

根据显著性水平α可得到临界值Zα/2，当|Z|>Zα/2时，拒绝原假设，认为系列存在趋势变化；否则，接受序列无趋势变化的原假设。本文统一取显著性水平α=0.05进行各种统计检验。

1.2.2 Spearman秩次相关检验

Spearman秩次相关检验[4,7 ]也是一种非参数检验方法。在运算时，将按时间顺序的原始序列xi(i=1，2，…n)从大到小排列并统一编号(从1开始)，每个数对应的编号定义为它的秩Ri，相同数的秩取编号的平均值。

原假设为序列无趋势性。统计量t由下式计算：

(4)

式中：rSRC为秩号-序号相关系数，其表达式为

(5)

式中：i为序列编号；di=RXi-RYi，RXi和RYi分别代表序号和秩号。

1.2.3 滑动t检验

滑动t检验是对传统t检验的改进，为搜索出变异点依次滑动，设变异点在不同位置n1(1≤n1≤n-1)，每次把连续的序列x分成2个子样本,即(x1,x2,…,xn1)和(xn1+1,xn1+2,…,xn1+n2)，其中n1+n2=n。滑动t检验的原假设为：变异点前、后2个子样本来自均值相同的总体。统计量t由下式计算：

(6)

式中:n1，n2为2个子样本的容量；a1，a2为2个子样本的均值；s1，s2为2个子样本的均方差。

1.2.4 滑动秩和检验

设分割点τ0前后2序列总体的分布函数各为F1(X)和F2(X)。从总体F1(X)和F2(X)中分别抽取容量为n1和n2的的2个子样本(n1+n2=n)，对F1(X)=F2(X)这一假设进行检验。将2个样本数据依大小次序从小到大排列并统一编号，规定每个数据在排列中所对应的序数为该数的秩，对于同样的数值，则用它们序数的平均值作为秩。记容量小的样本各数值的秩之和为W，秩和检验就是根据统计量U作检验的，当n1>10，n2>10时，U近似服从正态分布。统计量U可由下式计算：

(7)

式中:n1为小样本容量；n2为大样本容量。

根据显著性水平α可得到临界值Uα/2，当|U|>Uα/2时，拒绝原假设；否则，接受原假设。滑动秩和检验中，为搜索出变异点，依次滑动设变异点在不同位置τ0(1≤τ0≤n-1)，对应不同的变异位置τ0，将得出一系列统计量U，找出满足|U|>Uα/2所有可能的点τ0，选取使统计量|U|达最大值的点，作为最有可能发生变异的位置[8]。

1.2.5 Pettitt检验

Pettitt检验是非参数检验[9-10]，因此较少受到序列特异值的影响，能够较好地处理偏态分布的年极值序列。

假设一长度为n的时间序列xt(t=1，2，… ，n)，定义统计量如下式：

(8)

(9)

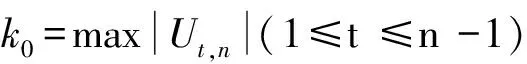
(10)

若P0≤0.5，则认为t0点为统计上显著的变点。由此检测出序列的一级变点，然后以该变点为界将原序列一分为二，继续检测新的变点。重复上述步骤，可检测出多级变点。

2 结果与分析

2.1 潮位序列的趋势检测结果

采用Mann-Kendall检验和Spearman秩次相关检验对2站3种不同的年潮位序列进行趋势检测。在0.05显著性水平下，Mann-Kendall检验的临界值Zα/2=1.96，Spearman秩次相关检验的临界值tα/2=2.002。趋势检测结果见表1。

表1 镇江和江阴站潮位趋势检验结果

表2 镇江和江阴站潮位变异点识别结果

从表1可以看出，2种检验的结果一致：镇江站年最高、最低潮位的统计量值均远远大于显著性水平α=0.05时对应的临界值，呈明显上升趋势；其年平均潮位的统计量值小于显著性水平α=0.05时对应的临界值，变化不显著，但表现出弱增加的趋势。而江阴站除年最高潮位上升趋势显著外，其年平均和年最低潮位变化趋势均不显著。此外，镇江站各个序列和江阴站年最高潮位序列的Kendall倾斜度依次达到了0.150，0.067，0.030，0.068 m/(10 a)。2站不同潮位的线性上升趋势见图1。

图1 镇江和江阴站年最高、最低和年平均潮位序列趋势

2.2 潮位序列变异点识别

采用滑动t检验法、滑动秩和检验法以及Pettitt检验法对2站3种不同的年潮位序列进行突变点识别。在0.05显著性水平下，滑动t检验的临界值tα/2=2.002，滑动秩和检验的临界值Uα/2=1.96。检测结果见表2。

由表2可知：对每一潮位而言，滑动t检验、滑动秩和检验以及Pettitt检验的结果基本相同。对于镇江站，其年最高潮位和年平均潮位，最为显著的突变都发生在1979年；其年最低潮位最为显著的突变发生在1987年。对于江阴站，其年最高潮位的显著突变发生在1979年，而年平均和年最低潮位均未有显著突变发生。2站不同潮位序列的变异如图2所示。

图2 镇江和江阴站年最高、最低和年平均潮位序列变异

3 潮位变异原因分析

长江镇江、江阴段为感潮河段，受径流和潮流的共同影响，其潮汐为不规则的半日潮型，涨落变化有明显的规律性[11]。下面以年最高潮位为例，从4个角度分析2站潮位变异的原因。

3.1 上游径流

长江作为我国第一大河，拥有巨大的径流量。安徽大通水文站作为长江干流下游区的控制站，亦可作为镇江、江阴段上游径流的代表站。若大通站流量发生显著变化，则其潮位也会受到一定的影响。镇江和江阴站年最高潮位的发生与大通站年最大流量有较好的同步性，分析大通站1953—2008年的年最大流量序列的变化趋势，取0.05显著性水平，M-K检验和Spearman秩次相关检验的结果见表3。可见，2种检验的统计量值均小于0.05显著性水平对应的临界值，变化趋势不显著。但由统计量值的符号可知，大通站年最大流量序列呈弱增加的趋势。

表3 大通站年最大流量序列的趋势检验结果

3.2 下游海平面

由于全球气候变暖，冰川消融、海洋表面水体热膨胀等导致了全球海平面上升。根据《2009年中国海平面公报》公布的数据：“近30 a来，中国沿海海平面总体呈波动上升趋势，平均上升速率为2.6 mm/a，高于全球海平面平均上升速率。南部沿海(长江口以南)海平面升幅高于北部沿海(长江口以北)，预计未来30 a，中国沿海海平面还将继续上升，比2009年升高80～130 mm。”根据长江口外验潮站大戢山站1978年1月—2006年12月、嵊山站1996年1月—2006年12月的实测潮位资料统计，2个站的海平面上升速率分别为4.0 mm/a和6.3 mm/a。海平面上升，不仅使入海径流受潮流的顶托作用加强，还由于水深增大而使波浪作用增强，同等情况下风暴增水加剧，这些都具有抬高长江潮位的效应[12]。根据龚政等[13]的研究，长江口海平面上升导致感潮河段水位抬升的幅度随着距河口距离的增大而减小，在张家港—十一圩附近分为上下2段，上段的抬升速率为1～2.5 mm/a(江阴站处于此段)，下段的抬升速率为4～6 mm/a，而镇江站距离河口300 km以上，海平面上升对其水位的抬升效应微乎其微。

3.3 区间水力特性

选取历年镇江站和江阴站年最高潮位及其相应的大通站日平均流量(考虑径流传播时间)，分1950—1978年、1979—2009年两阶段，点绘其年最高潮位与相应大通日平均流量的关系，见图3。

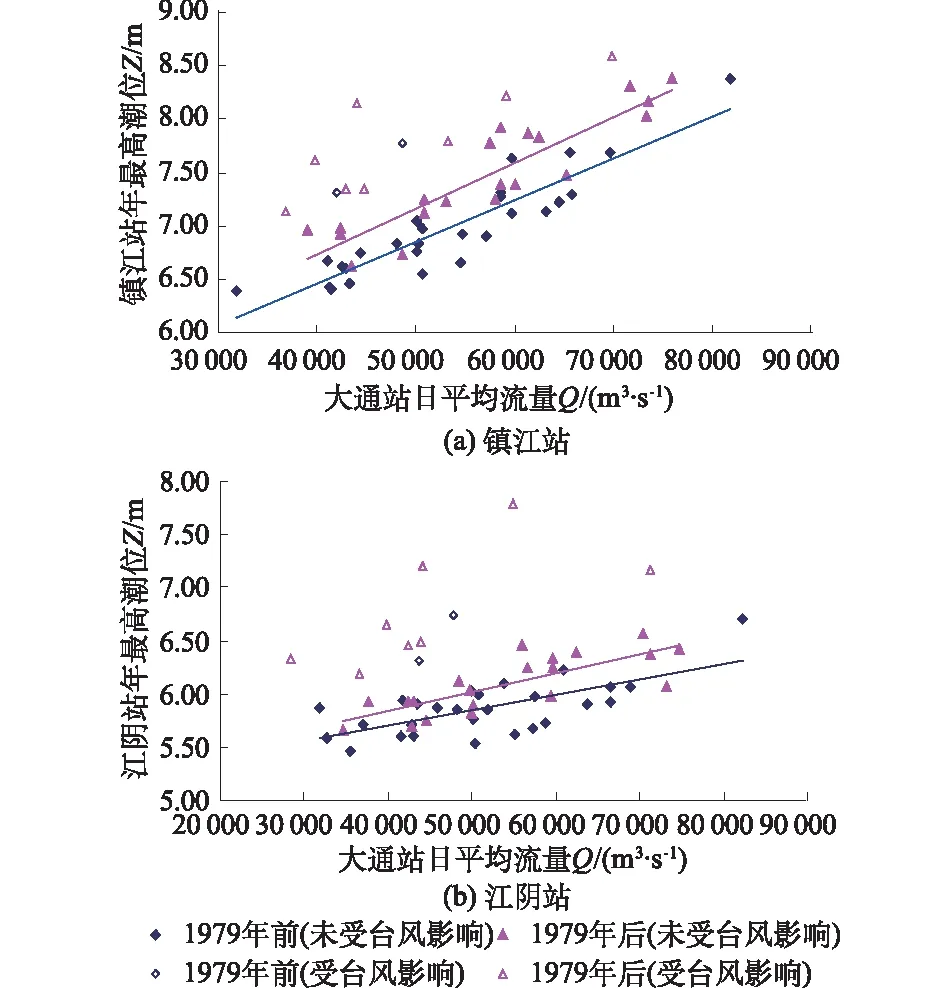
图3 镇江和江阴站年最高潮位与大通站相应日平均流量关系

从图3中可看出，相同时间阶段，受台风影响和不受台风影响的点据明显分群，这是由于2种情况下2站年最高潮位的形成机理明显不同。排除台风影响，根据未受台风影响的样本分析水位-流量关系，可见1979年前、后相关关系发生明显变化，对应相同大通流量，后期的年最高潮位显著高于前期。从另一角度证明镇江和江阴站年最高潮位确实发生了变异，同时间接说明区间的水力特性发生了改变。导致区间水力特性改变的具体原因较多，如：随着人类对长江沿线资源的开发，许多城市根据自身发展的需要并港建闸，并依据当地水情调整闸门的启闭以达到防洪排涝、蓄淡灌溉的最佳效益，较大程度上破坏了长江干流与各支流水量的天然连通性，改变了支流进入长江干流的水量及长江干流进入各支流的水量；还有围垦江滩使得河槽的容蓄能力降低，致使干流潮位抬高等。

3.4 极端气象条件

在理论上随着气候变暖，风暴潮的强度和发生频率也会增加。从图3中可知，对受台风影响的若干年份，镇江站年最高潮位明显抬升，普遍高于相同流量下未受台风影响的相应潮位。其中，对镇江和江阴站年最高潮位造成影响的台风在1979年前为2场(5612和7413号台风)，而在1979年后多达8场(除共同的8114，9608，9711，0012，0216号台风、2005年的“麦莎”台风和2006年的“帕丽斯”台风外，分别有9120和9216号台风)。可见，1979年后台风活动频度增加也是造成长江口年最高潮位抬升的原因。

4 对水文设计的影响

水文设计的任务是推求流量、水位、雨量等水文要素在指定设计标准下的设计值，为各种水利工程或涉水工程确定的规划设计和运行管理提供依据。而水文资料是进行水文设计的重要基础，当水文资料由于自然或人为原因发生阶段性改变，势必会对水文设计的科学性和可靠性产生影响。下面仍以镇江和江阴站年最高潮位序列为例，分析潮位变化对水文设计的影响，主要包括以下2方面：

(1) 破坏了水文序列一致性，使水文频率分析的难度增加，设计成果的可靠性降低。

传统的水文频率分析建立在样本序列满足独立、同分布的基础上，要求其满足一致性。就镇江站年最高潮位而言，序列已发生变异，倘若继续采用传统的水文频率分析方法进行处理，将使设计结果的不确定性增大[14-15]，而国内对于非一致性序列频率分析的研究又较少，主要集中在基于序列一致性修正[16-17]和基于序列时变与稳态成分的分解与合成[18]2个方面，且均存在一定的误差，在增加水文频率分析难度的同时，降低了设计成果的可靠性。

(2) 设计高潮位出现频率增加，重现期缩短，降低了水文设计值的防洪标准。

随着镇江和江阴站年潮位的整体抬升，原来的设计高潮位出现的频率将随之增大，且增加的幅度是非线性的，呈指数递增规律[19]，进而导致设计值的重现期缩短。为更直观地描述两站年最高潮位设计值的变化，以年最高潮位序列变异点1979年为分界点，将其分为1950—1978年和1979—2009年两阶段，分别进行频率分析。频率分析所采用的总体分布线型为P-Ⅲ型，参数估计采用线性矩法并结合目估适线法微调。通过频率分析得到两站1950—1978年、1979—2009年最高潮位的概率分布见图4。统计参数及不同频率的设计年最高潮位见表4。

图4 镇江和江阴站分段年最高潮位频率曲线

从图4可知，在分界点前后，镇江和江阴站年最高潮位的频率分布发生了明显变化，相同频率下的设计潮位显著抬升。对镇江站，0.1%，0.5%，1%，2%，10%频率的设计值均抬升了0.5 m左右；对江阴站，随设计频率增大，相应设计值的抬升幅度减小(频率从0.1%增大到10%，设计值的抬升量从0.7 m降至0.4 m左右)。在第1阶段，镇江年最高潮位超过9.18，8.69，8.47 m的概率分别为0.1%，0.5%和1%(重现期分别为1 000，200，100 a)；江阴年最高潮位超过7.55，7.15，6.98 m的概率分别为0.1%，0.5%和1%。而在第2阶段，镇江年最高潮位超过其原有3个设计值的概率依次增大为0.6%，2.7%和5.1%(重现期分别缩短为182，38，20 a)；江阴站年最高潮位超过其原有3个设计值的概率依次增大为1.0%，3.7%和6.0%(重现期分别缩短为100，27，17 a)。可见，由于年最高潮位的非一致性变化，原有的千年一遇潮位可降至几百年一遇，百年一遇潮位可降至几十年一遇，大大降低了水文设计值的防洪标准，致使防汛墙的防护标准降低，影响江苏沿江水利工程防潮防汛效用的发挥。

表4 镇江和江阴站年最高潮位分段样本的统计参数和设计值对比

在此需要说明，本文以统计推断得出的最佳分割点为界，对年最高潮位进行分段样本的频率计算，分段样本的容量在30左右，代表性是相对不足的，其频率分析结果仅用于说明由于年最高潮位的非一致性变化引起的概率分布变化是如此显著。借此向有关专业技术人员和行业管理单位强调，在该河段相关工程的规划设计和运行调度中必须充分考虑环境变化引起的水情变化。

5 结 语

通过对镇江和江阴站近60 a(1950—2009年)年最高、最低以及年平均潮位序列的非一致性检验及比较分析，得到以下结论：

(1) 镇江站年最高、最低及年平均潮位均呈上升趋势。其中，年最高潮位趋势变化最为显著，年最低潮位次之，年平均潮位变化不显著。年最高和年平均潮位均在1979年前后发生显著突变，而年最低潮位在1987年前后发生突变。江阴站仅年最高潮位呈显著上升变化，且在1979年左右发生显著突变，年平均和年最低潮位趋势变化不显著，且未发生显著变异。

(2) 影响镇江和江阴站潮位变化的上、下边界条件(即上游径流和下游潮流作用)相似，故一般情况下2站的潮位变化特性应存在相似性。本次分析表明，2站的年最高和年平均潮位具有一致的变化趋势，但年最低潮位的变化趋势存在差异，这可能是由2站附近的局部地形变化不同所致，也可能与年最低潮位受其影响的程度不同有关。

(3) 从上游径流、下游海平面、区间水力特性、极端气象条件等4个方面初步分析了镇江和江阴年最高潮位发生变异的原因，表明由于沿江支流口门纷纷建闸控制水流及围垦江滩等导致河段水力特性改变、气候变化导致极端风暴潮天气频发是主要原因。

(4) 镇江和江阴站年潮位的这种非一致变化现象对水文设计的科学性和可靠性产生一定影响，主要包括增加了水文频率分析的难度和降低了年最高潮位设计值的防洪标准两方面。因此，要在充分重视其影响的基础上，及早采取相关对策和措施，对防汛墙、海堤等水工建筑物进行加高加固，确保江苏沿江沿海水利工程发挥其应有效用。

(5) 2009年三峡工程具备正常运行条件后，对下游潮位，尤其是高、低潮位会有一定影响。鉴于本文研究的是1950—2009年的潮位序列，且2009年后至今仅4 a左右，样本代表性不足，故暂未就三峡水库运行对下游潮位的影响进行分析，有待资料积累后进一步研究。

[1] 梁忠民, 胡义明, 王 军. 非一致性水文频率分析的研究进展[J].水科学进展, 2011,22(6): 864-871. (LIANG Zhong-min, HU Yi-ming, WANG Jun. Advances in Hydrological Frequency Analysis of Non-stationary Time Series[J]. Advances in Water Science, 2011,22(6): 864-871. (in Chinese))

[2] SONALI P, KUMAR D N. Review of Trend Detection Methods and Their Application to Detect Temperature Changes in India[J]. Journal of Hydrology, 2013, 476: 212-227.

[3] 谢 平, 许 斌, 谭莹莹, 等. 变化环境下地表水资源评价方法研究综述[J].河海大学学报(自然科学版), 2010,38(2): 59-62. (XIE Ping, XU Bin, TAN Ying-ying,etal. Review of Study on Methods of Surface Water Resources Evaluation under Changing Environment[J]. Journal of Hohai University(Natural Sciences), 2010, 38(2): 59-62. (in Chinese))

[4] 丁 晶, 邓育仁. 随机水文学[M] . 成都：成都科技大学出版社, 1988: 41-54. (DING Jing, DENG Yu-ren. Stochastic Hydrology[M]. Chengdu: Chengdu University of Science and Technology Press, 1988: 41-54 (in Chinese))

[5] 于延胜, 陈兴伟. R-S和Mann-Kendall法综合分析水文时间未来的趋势特征[J]. 水资源与水工程学报, 2008,19(3):41-44.(YU Yan-sheng, CHEN Xing-wei. Analysis of Future Trend Characteristics of Hydrological Time Series Based on R-S and Mann-Kendall Methods[J]. Journal of Water Resources & Water Engineering, 2008,19(3): 41-44. (in Chinese))

[6] 王金花, 康玲玲, 赵广福. 基于Mann-Kendall法的水沙系列突变点研究[J].人民黄河, 2010,32(1):42-45. (WANG Jin-hua, KANG Ling-ling, ZHAO Guang-fu. Analysis of Change Point Detection of Water and Sediment Series based on Mann-Kendall Method[J]. Yellow River, 2010,32(1):42-45. (in Chinese))

[7] 王国庆, 张建云, 贺瑞敏. 黄河中游气温变化趋势及其对蒸发能力的影响[J]. 水资源与水工程学报, 2007,18(4):32-36. (WANG Guo-qing, ZHANG Jian-yun, HE Rui-min. Trends of Temperature Change in Middle of Yellow River and Its Impact to the Evaporation Potential[J]. Journal of Water Resources & Water Engineering, 2007,18(4):32-36. (in Chinese))

[8] 雷红富, 谢 平, 陈广才, 等. 水文序列变异点检验方法的性能比较分析[J].水电能源科学, 2007,25(4):36-40. ( LEI Hong-fu, XIE Ping, CHEN Guang-cai,etal. Comparison and Analysis on the Performance of Hydrological Time Series Change-point Testing Method[J]. Water Resources and Power, 2007,25(4):36-40. (in Chinese))

[9] LIN Xue-dong, ZHANG Yi-li, YAO Zhi-jun,etal. The Trend on Runoff Variations in the Lhasa River Basin[J]. Journal of Geographical Sciences, 2008, 18(1):95-106.

[10]PETTITT A N. A Non-Parametric Approach to the Change-Point Problem[J]. Journal of the Royal Statistical Society. Series C (Applied Statistics), 1979, 28(2): 126-135.

[11]夏云峰, 闻云呈, 梁 婷. 长江下游典型代表性潮型选择研究初探[J]. 水道港口, 2010, 31(5):501-505.(XIA Yun-feng, WEN Yun-cheng, LIANG Ting. Primary Research on Typical Representative Tidal Type Selection in the Lower Yangtze River[J]. Journal of Waterway and Harbor, 2010, 31(5): 501-505. (in Chinese))

[12]李加林, 张殿发, 杨晓平, 等. 海平面上升的灾害效应及其研究现状[J]. 灾害学, 2005, 20(2): 49-53. (LI Jia-lin, ZHANG Dian-fa, YANG Xiao-ping,etal. Disaster Effect of Sea Level Rise in China and the Research Status in Quo[J]. Journal of Catastrophology, 2005, 20(2): 49-53. (in Chinese))

[13]GONG Z, ZHANG C K, WAN L M,etal. Tidal Level Response to Sea-level Rise in the Yangtze Estuary[J]. China Ocean Engineering, 2012, 26(1): 109-122.

[14]TODOROVIC P, ROUSSELLE J. Some Problems of Flood Analysis[J]. Water Resources Research, 1971, 7(5): 1144 -1150.

[15]SCHMOCKER-FACKEL P, NAEF F. More Frequent Flooding? Changes in Flood Frequency in Switzerland Since 1850[J]. Journal of Hydrology, 2010,381(1/2):1-8.

[16]陆中央. 关于年径流量系列的还原计算问题[J]. 水文, 2000, 20(6): 9-12. (LU Zhong-yang. Restore Estimation of Annual Runoff Series[J]. Hydrology, 2000, 20(6): 9-12. (in Chinese))

[17]李国芳, 陈阿平, 华家鹏. 设计潮位计算中若干问题探讨[J]. 水电能源科学, 2006, 24(3): 35-38. (LI Guo-fang, CHEN A-ping, HUA Jia-peng. Problems and Improvements in Design Tidal Level Calculation[J]. Water Resources and Power, 2006, 24(3): 35-38. (in Chinese))

[18]李国芳.长江感潮河段工程水文研究[M]. 南京：河海大学出版社, 2013: 66-68. (LI Guo-fang. Study on Engineering Hydrology in the Tidal Reach of the Yangtze River[M]. Nanjing: Hohai University Press, 2013: 66-68. (in Chinese))

[19]都金康, 史运良. 未来海平面上升对江苏沿海水利工程的影响[J]. 海洋与湖沼, 1993,24(3): 279-285. (DU Jin-kang, SHI Yun-liang. Impact of Future Sea Level Rise on Water Projects in Coastal Area of Jiangsu Province[J]. Oceanologia et Limnologia Sinica, 1993,24(3): 279-285. (in Chinese))

(编辑：赵卫兵)

Nonstationarity of Tidal Level and Its Impacts onHydrologic Design in Yangtze River Estuary

ZHANG Yue, LI Guo-fang

(College of Hydrology and Water Resources, Hohai University, Nanjing 210098, China)

According to the data of annual maximum and minimum tidal levels as well as annual mean tidal levels of Yangtze River recorded in Zhenjiang and Jiangyin Stations, the trends of the three tidal level time series from 1950 to 2009 were detected by using two non-parametric statistical methods (Mann-Kendall test and Spearman rank correlation test), and the jumps of the above three tidal level time series were examined with three test methods namely moving t-test, moving rank sum test and Pettitt test. All the results were of high coincidence, showing that there were significant rising trends in both annual maximum and minimum tidal levels, while such rising trend in annual mean tidal levels was insignificant at Zhenjiang Station. For Jiangyin Station, only the annual maximum tidal level had obvious rising trend, while the trends of the annual mean and minimum tidal level were not significant. Results of the three tests for jumps showed that the most significant abrupt changes in annual maximum and annual mean tidal level time series occurred mostly around 1979 and an abrupt change in annual minimum tidal level took place in 1987 at Zhenjiang Station. A significant abrupt change in annual maximum tidal level at Jiangyin Station also occurred in around 1979, but there were no significant variation detected in its annual mean and minimum tidal level. With annual maximum tidal level as an example, the causes of tidal level rise were analyzed. This nonstationarity of tidal level might generate negative impacts on hydrologic design, including the increase in difficulty of hydrologic frequency analysis and the decrease in flood control standards of hydrologic design values.

annual maximum tidal level; annual minimum tidal level; annual mean tidal level; nonstationarity; hydrologic design

2014-01-26;

2014-04-19

国家自然科学基金资助项目(51109053，51190091)

张 悦(1990-)，女，江苏南通人，硕士研究生，研究方向为水文学及水资源，(电话)15195872198 (电子信箱) yzhang9001@163.com。

李国芳(1971-)，女，浙江杭州人，教授，研究方向为水文学及水资源，(电话)025-83787499(电子信箱)liguofang@hhu.edu.cn。

10.3969/j.issn.1001-5485.2015.05.005

2015,32(05):21-27,36

P333

A

1001-5485(2015)05-0021-07