平移亦旋转—对一类图形变化题目的思考
山东省泰安第六中学 刘向炜 娄延贞
山东教育出版社出版的《义务教育教科书(五•四制)数学》八年级上册,第四章图形的平移与旋转,第四节图形变化的简单应用,这一节内容将图形的轴对称、平移、旋转整合在图案的欣赏和设计活动中,丰富有趣。在笔者的教学过程中,此章节深受学生们的喜爱,尤其是课本P107页的做一做,这一小节中,大家各抒己见,发现了好多种变化的方法。因为此图形较为复杂,加上手工作图的局限性,并没有学生说出“树甲”可以经过一次旋转变换就可以与“树乙”重合。但这并不代表学生们想不到。由于课后P108页的习题2 ,《教师用书》中给出了四种图形变化方式,大多数老师也都给学生讲解了多种变化方法,当然也包括经过一次旋转可以完成题目要求的变换;再加上《配套练习册》P107页的探索尝试的对比,有很多学生提出了课本P107页做一做的“那棵树”能不能经过一次旋转变换完成由“树甲” 到“树乙”的变化?对于这个问题,大多学生会得到这样的回答:你亲自动手做一做,利用尺规作图方法作出对应点连线中垂线,看看他们能不能交于一点就可以了,但是很少有人给出明确的答案。因为多数人心里想的是大概吧,也许吧,或许可以,应该行。也就是因为这一点,所以才会有很多辅导资料上会出现有两个正确答案的选择题。比如,山东教育出版社出版的《初中数学基础训练》,还有发行量很高的《少年智力开发报•数学专页》上均有这类题目。《基础训练》P130页的这道题,它与我们教科书上的课后习题2,变化方式一样,《教师用书》中也已经明确给出了四种变换方式,包括只用旋转即可完成,当然不能只选答案D了。《少年智力开发报•数学专页》期末综合训练A卷上也有这样一道题(题目图片见文章最后)。这种题目的存在,说明了很多人(包括老师)没有认识到“平面上的图形变化,凡是经过平移、旋转能够完成的,完全可以经过一步旋转完成”这一事实,也就是“两步变一步”。于是笔者带着这个问题和同事们展开了研究,经过讨论、作图,严格的数学推理,最终证明了这一命题是真命题。下面我来说一下证明的思路,以及证明的过程。
从平面内基本图形线段入手,把一条线段AB先平移一段距离后,再旋转某个角度,完成线段AB到线段A1B1的变化。若要证明线段AB可以经过一次旋转变化到线段A1B1,那么必须得说明变化前后的两条线段上所有的对应点的连线的中垂线都经过一个点,这个点就是旋转变化时的旋转中心。于是就有了下面的证明过程。
已知如图平面直角坐标系中,线段AB在y轴正半轴上A(0,0),B(0,a),把线段AB沿x轴向右平移b个单位后,到达A1B’处,然后让线段A1B’绕点A1顺时针旋转θ度,变成线段A1B1,求证:线段AB与线段A1B1所有对应点的连线的中垂线经过同一个点。
证明:过点B1作B1D⊥x轴,垂足为D,易得可得线段的点坐标利用待定系数法可设直线表达式为:y=m1x+a,把代入可解得于是直线表达式为:因为互相垂直的两条直线表达式的一次项系数乘积为-1,所以可以设直线中垂线表达式为:把线段的中点代入可求得
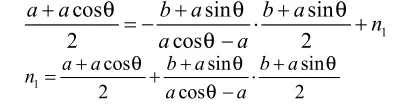
可以得到线段的中垂线表达式应为此直线与线段的中垂线的焦点可以求出来,计算如下:
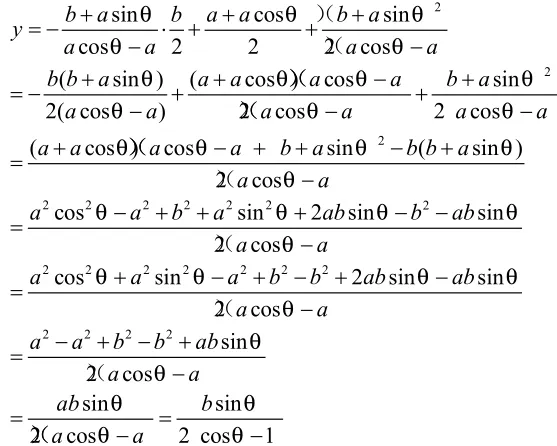
直线的方程可以设为y=m2x+ka,把代入可解得于是直线表达式为:因为互相垂直的两条直线表达式的一次项系数乘积为-1,所以可以设线段CC1的中垂线表达式为:把线段的中点代入可求得
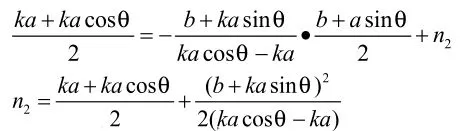
所以直线的中垂线方程为:此直线与线段的中垂线的交点坐标应为

所以交点为,这与前边所求的交点坐标相同。
这在理论上证明了两条线段上所有的对应点的连线的中垂线都经过一个点。所以“二步变一步”是正确的。后来笔者通几何画板软件,做了“这棵树”的动画图片,又从另一方面印证了:平面图形平移、旋转变换完全可以用一步旋转完成。毫无疑问当旋转中心离我们要旋转的图形很远很远,并且我们的旋转角度足恰好又很小,此时的图形变换就是平移,所以我们可以说平移亦旋转,平移恰好是转的一个特殊情况,是旋转中心无限远的一个特例。
一番探索研究下来,我本人收获了以下几点:一是在教育教学的过程中,我们教师对于每一个小细节都要认真思考,严谨证明,尤其是教给学生们的知识上,更要严苛的要求自己。二是这种研究会让我们有很多意想不到的收获,可以得出一些从未有人研究的过结论,享受探究的乐趣,并能潜移默化给自己的学生们。三是正如旋转亦平移是正确的一样,我们可以推理出这样的事实:两平行线在无限远的地方是有交点的。这一点以后有机缘再深入研究。

