模糊自整定PID控制器在光电伺服设备中的应用

周俊鹏，李焱

（1.中国科学院长春光学精密机械与物理研究所，吉林长春130033；2.长春工业大学电气与电子工程学院，吉林长春130012）

PID 控制器一直是控制领域中应用最广、最成熟的控制器。将智能模糊控制和经典PID 控制以不同的方式结合，可以利用各自的优势，有效提高控制系统性能［1］。工业控制系统越来越复杂仅仅用单纯的PID 控制已经无法满足工业控制的需要［2］，为适应不同控制对象，需要人工重新整定控制器参数，进而设计开发模糊PID 控制器并进行了试验仿真，没有给出控制精度改善情况。模糊PID 自整定控制与传统PID 控制相结合应用广泛，特别是温度控制、汽车、液压机床方面应用较多［3-5］。基于模糊PID 控制的直流伺服系统，实现了在线实时PID 参数整定，验证了该方法在超调量，调节时间方面比常规PID控制理想，但没有提到控制精度方面的指标。通过模糊控制使得PID 的参数实时在线调整，使其更好地兼顾系统的静态和动态性能，以便提高系统的鲁棒性，但未提及系统快速性和控制精度方面的性能［6］。本文以模糊PID 算法应用在某型光电伺服设备位置环中，在超调量和快速性以及跟踪误差方面取得了良好的效果。与传统PID 控制相比，其阶跃误差少了0.08′，正弦引导最大误差少了1.4′，最小误差少了1′。解决了传统PID控制时跟踪误差不高的问题。

1 模糊自整定PID控制器的算法设计

1.1 各参量隶属函数的确定

输入变量|e|和|ec|语言值的模糊子集取为{负大，负中，负小，零，正小，正中，正大}，并简记为{NB，NM，NS，Z，PS，PM，PB}，论域为{-3，3}。以Δkp，Δki，Δkd3个参数作为输出变量。Δkp，Δki，Δkd模糊量的模糊子集取为{负大，负中，负小，零，正小，正中，正大}，并简记为{NB，NM，NS，Z，PS，PM，PB}。其中NB，PB取S形隶属度函数，其余取三角形隶属度函数。需要配合使用的增量式PID算式为

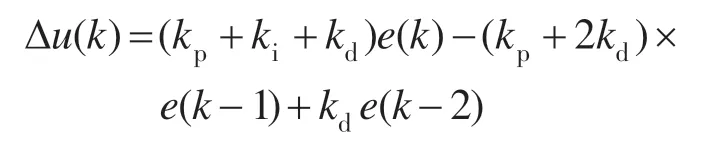
1.2 建立控制规则表

根据上述控制规则建立参数Δkp的模糊控制规则，如表1所示。参数Δki和Δkd的规则与Δkp类似。

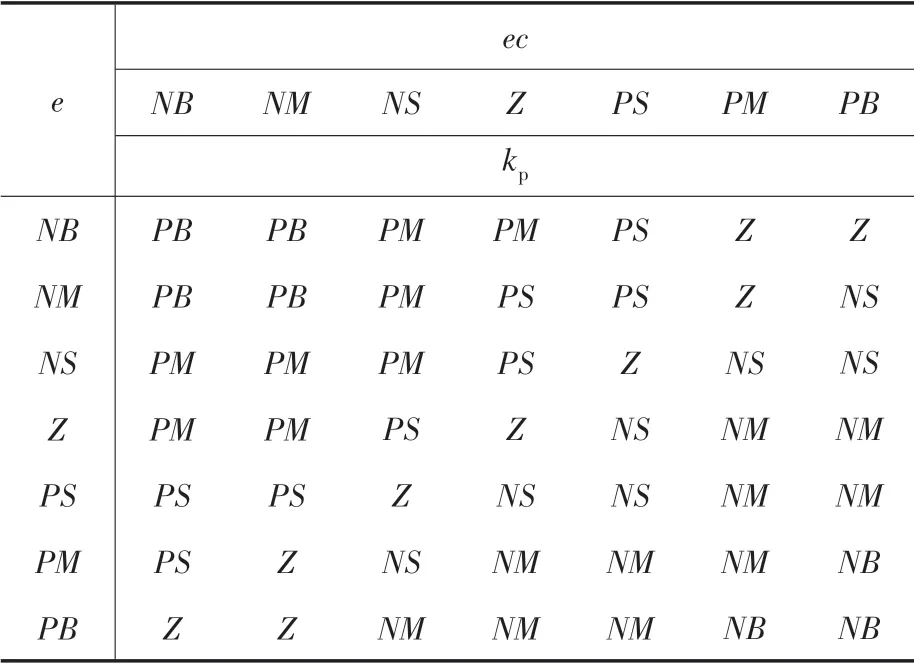
表1 Δkp模糊规则表Tab.1 Δkp fuzzy rule table

1.3 模糊推理和模糊运算

由模糊控制规则可知，各参数调节规则表可写成条件语句形式对于表1，Δkp的调节规则可以写成49条模糊条件语句如下：

1）if|e|=NB and|ec|=NB then kp=PB

2）if|e|=NM and|ec|=NB then kp=PB

3）if|e|=NS and|ec|=NB then kp=PM

⋮

那么对于第1条语句规则的隶属度的计算为

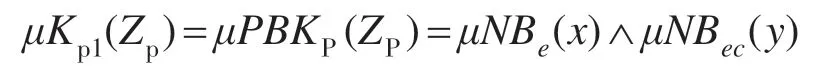
后面语句以此类推，可求得Δkp在不同的偏差|e|和偏差变化率|ec|条件下的所有模糊取值的隶属度。根据可求得Δkp的隶属度。最后再利用公式μ=∑xi×μN(xi)/∑μN(xi)进行模糊判决可得出相应的Δkp参数值。Δki和Δkd的参数值可用同样的方法求得。

2 模糊自整定PID控制系统的模块化

在Matlab中采用Mamdani推理法进行模糊推理与反模糊化。打开Matlab中的FIS编辑器，确定模糊控制器的结构为两输入（e，ec）、3输出（Δkp，Δki，Δkd），并确定输入、输出名。并根据三角隶属度函数和Sigmoid形隶属度建立对应的隶属函数。再根据前面介绍的模糊控制规则表，在Matlab中的RULE EDITOR中建立模糊控制规则。最后通过pid=readfis（‘fuzzypid.fis’）语句在Matlab 模块图形中嵌入上述模糊控制规则，使图1 中的Fuzzy Logic Controller模块与.fis文件建立连接。为了方便，在图1中建立子系统，令偏差和模糊控制的输出Δkp，Δki，Δkd做为输入，偏差经过PID运算和模糊控制的输出kd，ki，kp整合后作为子系统的输出。

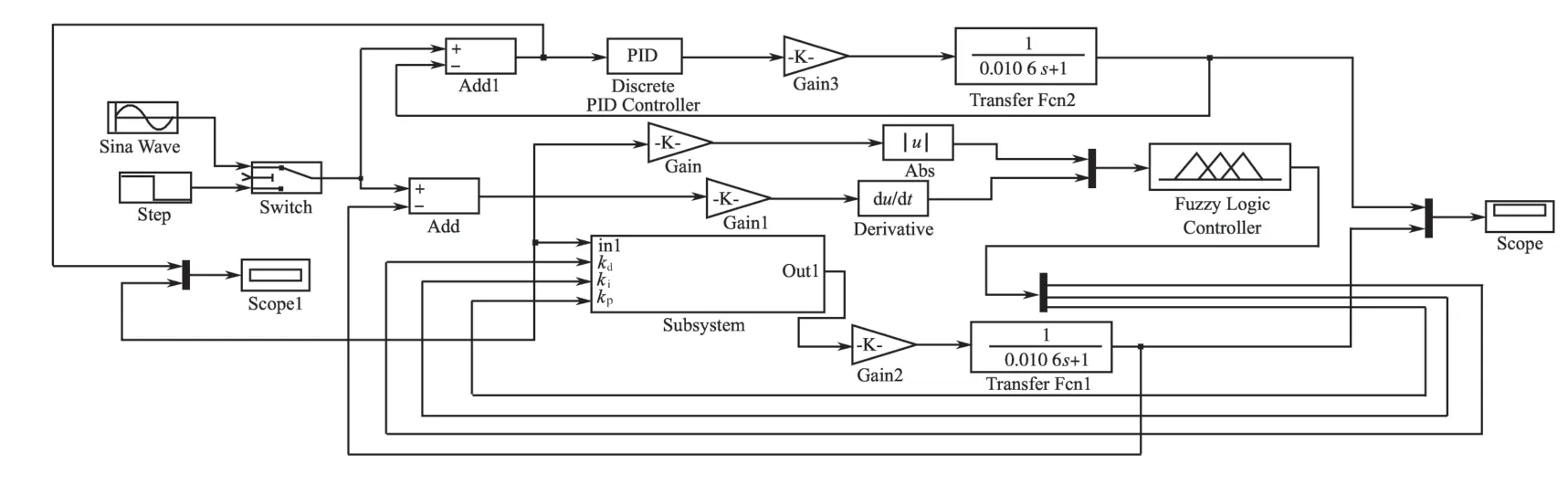
图1 模型方框图Fig.1 Moudle block diagram

3 系统仿真与实测

某型光电伺服设备最大速度为48(ο)/s、最大加速度为22(ο)/s2，则等效正弦为104.7 sin 0.458 3t。其位置回路应用模糊自整定PID 控制，速度回路等效惯性环节的传递函数为1/(0.010 6s+1) 将此传递函数代入图1中进行仿真。

在Matlab 中可得到模糊控制中的Δkp，Δki，Δkd。空间分布如图2所示。

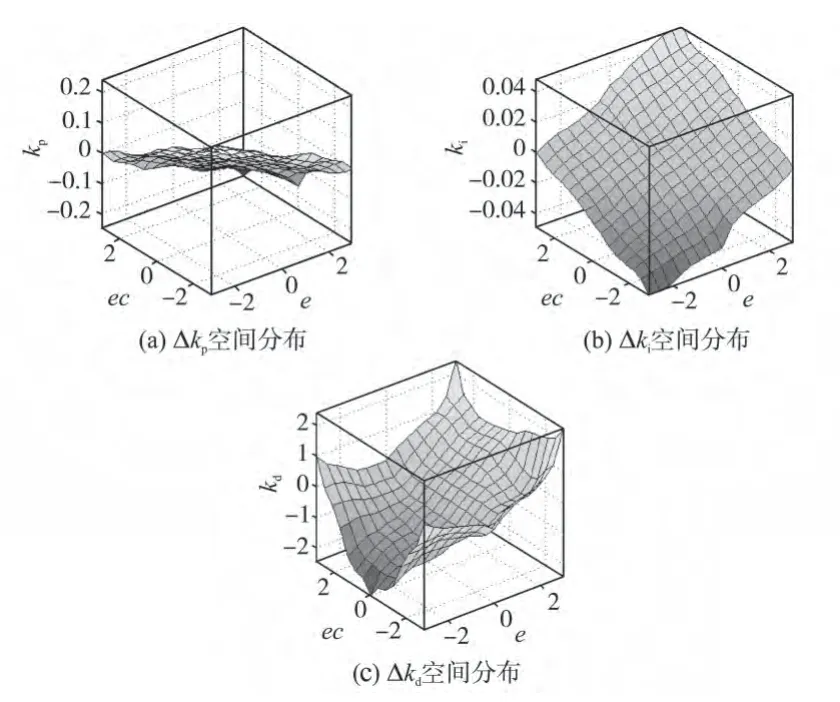
图2 模糊规则三维图Fig.2 Fuzzy rule three dimension diagram

从图2中可看到模糊控制输出的Δkp和Δkd论域为［-0.3，0.3］，Δki论域为［-0.06，0.06］。用图2在Matlab 中仿真可得到光电伺服设备的阶跃响应。为直观看出结果，现将模糊PID 控制与常规PID控制对比图合在一起得到图3和图4。

从图3、图4和图5中分析可得到表2。

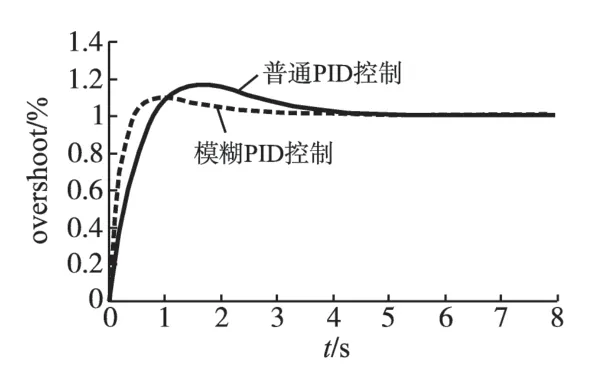
图3 阶跃响应对比图Fig.3 Step response comparison diagram

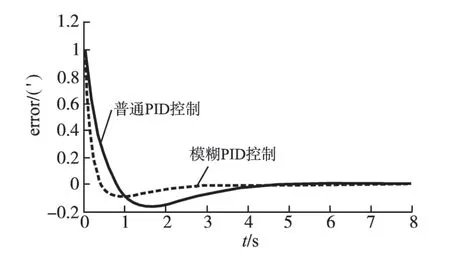
图4 阶跃误差对比图Fig.4 Step error comparison diagram

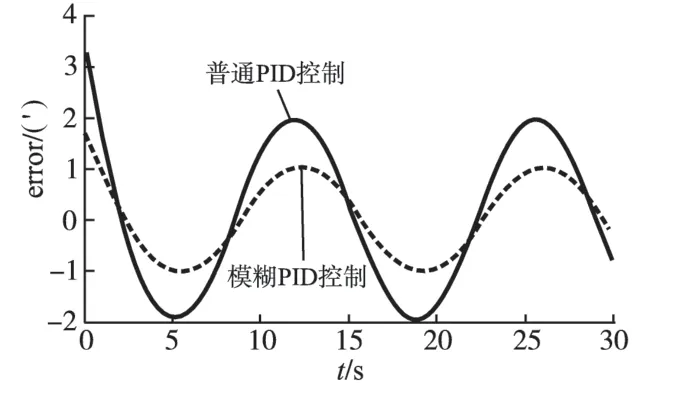
图5 等效正旋引导误差对比图Fig.5 Equivalent sine guide error comparison chart

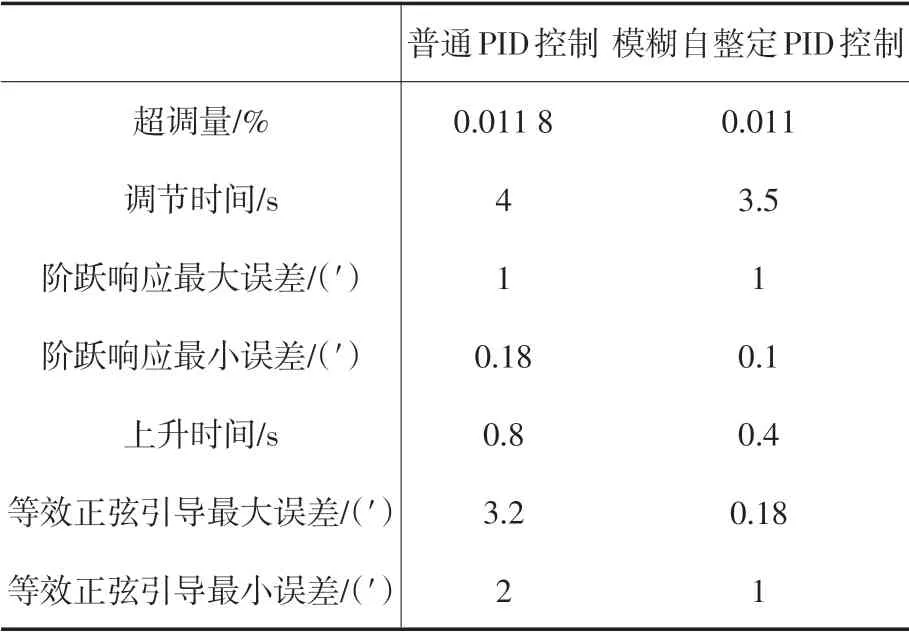
表2 性能对比表Tab.2 Comparison of performance table

由表2 中对比可知，使用模糊自整定PID 控制器控制光电伺服设备，使其超调量，调节时间，阶跃响应最小误差和上升时间方面均强于普通PID控制。可见模糊自整定PID在各个方面都有良好性能。用图2 中的光电伺服设备，跟踪方式选择中波红外在外场跟踪目标，将测得的脱靶量值、目标实测值以及目标实际位置值的数据导入Matlab 中处理得到实测误差如图6 和图7 所示。实际的目标捕获图如图8所示。

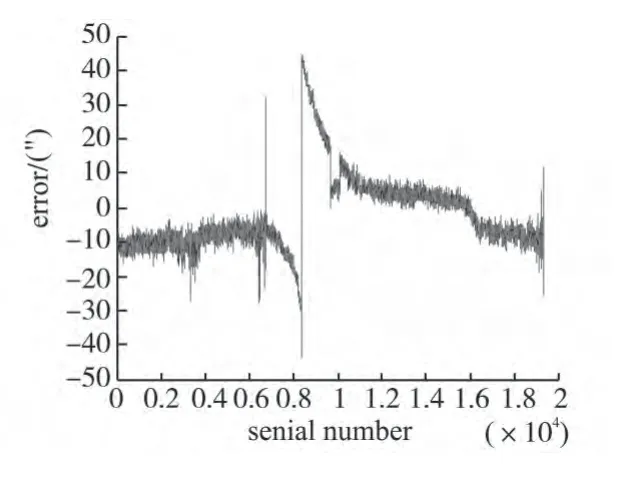
图6 普通PID控制误差图Fig.6 Common PID control error picture

从图6 和图7 实测误差图中可看出模糊PID自整定控制时，误差最大35″比普通PID 控制小了10″左右，最小误差为28″比普通PID控制小了13″。可见模糊PID 控制在跟踪目标的能力上远好于普通PID控制。

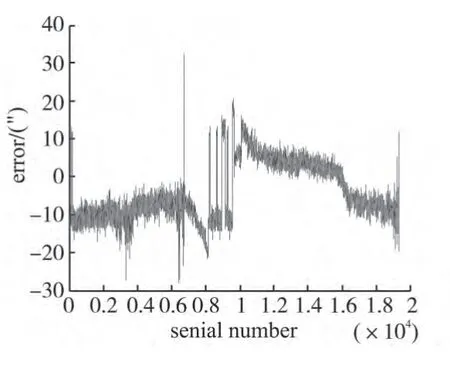
图7 模糊PID控制误差图Fig.7 Fuzzy PID control error picture

图8 目标捕获图Fig.8 Target acquisition picture

4 结论

经过试验对比分析可知，模糊自整定PID 控制器在控制方面优于普通PID控制器。从表2中可看出，模糊自整定PID 控制系统比普通PID 控制系统的阶跃响应的超调量减少了0.000 8%，调节时间少了0.5 s，阶跃响应最小误差少了0.08′，上升时间快了0.4 s，正弦引导最大误差小了1.4′，正弦引导最小误差小了1′。从图6 和图7中可知，用中波红外跟踪目标时跟踪误差最大仅为35″比普通PID控制小了10″左右。

［1］彭一峰.基于模糊PID 控制理论的振动主动控制研究［D］.大连：大连理工大学，2013.

［2］朱琰，李曼珍.模糊PID 控制方法的仿真和研究［J］.仪表技术，2013，1（12）：32-36.

［3］王忠康，张艳，赵海多，等.基于模糊PID控制的半导体激光器温度控制的仿真研究［J］.辽宁工业大学学报：自然科学版，2014，34（2）：79-81.

［4］赵树恩，刘文文，屈贤，等.基于PID参数模糊自适应的汽车EPS助力特性研究［J］.农业装备与车辆工程，2014，52（1）：19-31.

［5］杨晶，同志学，王瑞鹏，等.液压机械手电液比例系统模糊PID控制研究［J］.机械科学与技术，2013，32（6）：834-838.

［6］张贵，黄静华，夏永胜.基于PLC 的电液比例伺服系统的模糊PID控制研究［J］.机床与液压，2014，42（1）：83-85.

［7］李焱，曹立华，王弟男.惯导平台下舰载光电搜索跟踪系统的控制［J］.光学精密工程，2011，19（5）：1126-1123.

［8］Hwang C C，Li P L，Liu C T，et al.Design and Analysis of a Brushless DC Motor for Applications in Robotics［J］. IET Trans.on Electric Power Applications，2012，6（7）：385-389.

［9］Meza J L，Santibanez V，Soto R，et al. Fuzzy Self-tuning PID Semiglobal Regulator for Robo Manipulators［J］. IEEE Trans.on Industrial Electronics，2012，59（6）：2709-2717.

［10］周俊鹏，李焱，王一卉，等.舰载光电伺服设备的系统辨识研究［J］.液晶与显示，2014，29（5）：73-79.

［11］周俊鹏，李焱.机载平台下功率级驱动及PWM 死区控制的研究［J］.微特电机，2014，42（10）：35-38.