基于预测直接功率的双PWM一体化控制策略

王辉，徐雪刚，吴轩，钟立群

（湖南大学国家电能变换与控制工程技术研究中心，湖南长沙410082）

双PWM 变换器由整流器和逆变器组成，直流侧并联一个电解电容来抑制电压的波动。因此，如何减小直流侧电解电容的体积成为当前研究的课题［1-2］。

文献［2］通过在整流器的矢量控制系统中引入负载电流加入到电压环中作为前馈补偿，文献［3-4］通过引入电容电流控制，以电容电流为零作为控制目标，使得电流从整流器全部流向逆变器，从而抑制直流侧电压的波动。文献［5］通过将逆变器（主系统）的信息引入到整流器（从系统）控制系统中，实现协调控制。文献［6］从整流器和逆变器的瞬时功率平衡关系分析，对整流器和逆变器进行协调控制。

本文着重分析整流器的控制策略，提出一种基于直接功率控制理论的预测控制策略，分析整流器与逆变器的功率关系，将两者之间不平衡的功率信息作为功率补偿引入到整流器的控制回路中，实现协调控制。

1 双PWM变换器的数学模型

双PWM 变换器的拓扑结构如图1 所示，双PWM 变换器由PWM 整流器和逆变器通过并联直流侧组成，直流侧并联一个电解电容用于稳压，整流器侧接电网，逆变器侧接电机。

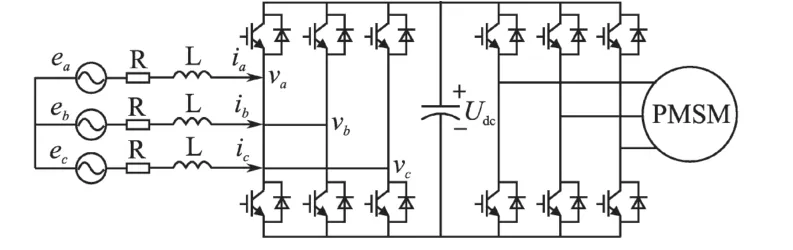
图1 双PWM变换器的拓扑结构Fig.1 Toplogical structure of AC-DC-AC PWM converter

图1中，ea，eb，ec为三相交流电网电压；ia，ib，ic为整流器网侧三相交流输入电流；va，vb，vc为整流器三相交流输入电压；Udc为直流母线电压；L，R分别为网侧滤波电感和电阻。

两相静止坐标系下建立电压型PWM整流器的数学模型为

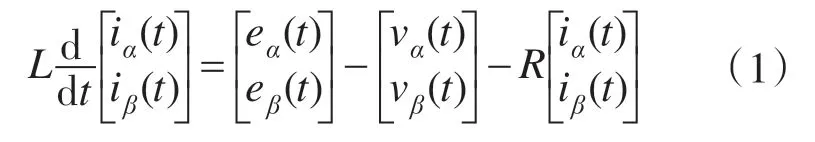
式中：eα，eβ分别为三相交流电网电压αβ坐标系分量；iα，iβ为整流器网侧输入电流αβ坐标系分量；vα，vβ为整流器交流输入电压αβ坐标系分量；L 为网侧电感；R为网侧电阻。

图1中电机为永磁同步电机，其数学模型为

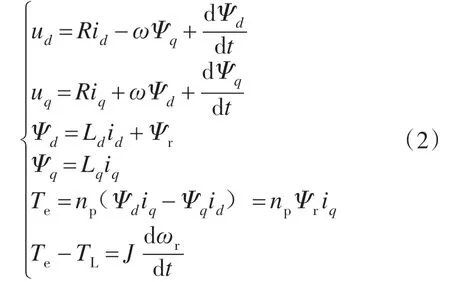
式中：R为定子电阻；ω’ωr分别为转子的电角速度和机械角速度；id，iq分别为d-q 轴电流分量；ud’uq分别为d-q轴电压分量；Ld，Lq分别为d-q轴电感分量；Ψd，Ψq分别为d-q轴磁链分量；Ψr为永磁体产生的磁链；np为转子极对数；Te为电磁转矩；TL为负载转矩；J为转动惯量。

2 PWM 整流器直接功率预测控制策略

在α-β两相静止坐标系下，瞬时功率表达式为

式中：P，Q分别为电网瞬时有功功率和瞬时无功功率；eα，eβ分别为三相交流电网电压αβ坐标系分量；iα，iβ为整流器网侧输入电流αβ坐标系分量。

采样周期为Ts时，设kTs时刻交流侧电源电压、整流器交流侧电压以及输入电流分别为e(k)’v(k)’i(k)。由于电阻很小，忽略电阻R带来的影响。对式（1）进行离散化，得：

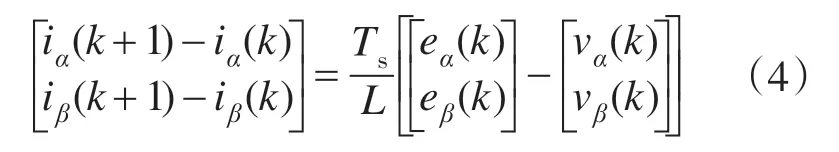
假设采样频率远大于电网电压频率，电源电压大小在相邻2 个采样周期可看作不变，即：e(k+1)与e(k)相等。因此，根据式（3），可得连续2个采样周期的瞬时功率改变量为

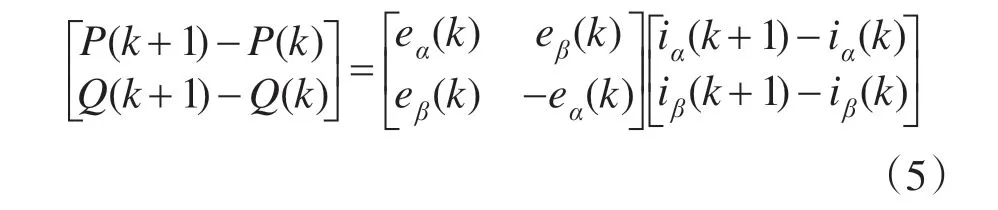
由于要使得控制对象的功率跟踪作为参考的下一个采样周期的功率，故定义

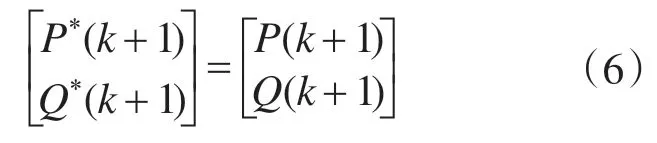
式中：P*(k+1)，Q*(k+1)为(k+1)Ts时刻的期望有功功率和无功功率。

将式（5）、式（6）代入式（4）可以得到

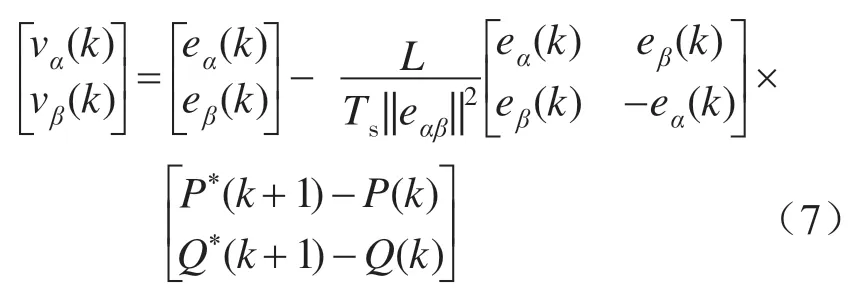
在直接功率控制策略中，整流器为实现单位功率因数控制，期望的无功功率Q*直接给定为0，而期望的有功功率P*由电压外环控制。

要实现在kTs时刻对（k+1）Ts时刻的预测，式（7）可以表示为

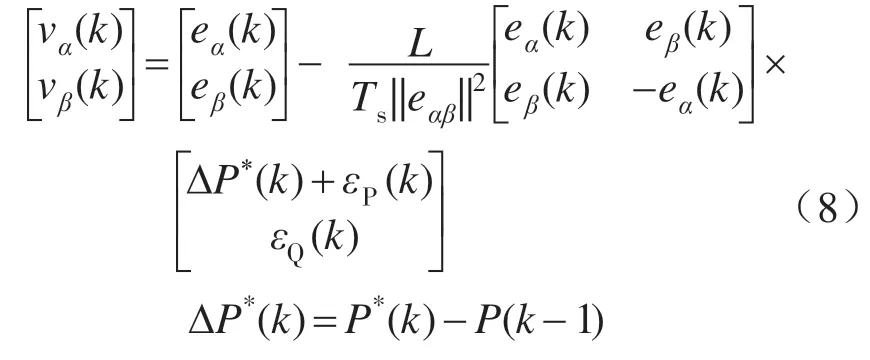
式中：εP(k)，εQ(k)分别为实际的有功功率和无功功率的跟踪误差。

3 双PWM变换器一体化控制策略

双PWM 协调控制策略的框图如图2 所示，双PWM 系统中，能量在三相电网与电动机负载之间流动，系统中电感和电容作为存储一部分能量，忽略能量流动中的开关损耗与电阻损耗，根据功率平衡原理可以得到整流器、逆变器与直流侧电容之间的功率关系

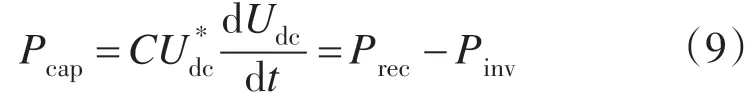
对式（9）进行拉普拉斯变换可以得到：

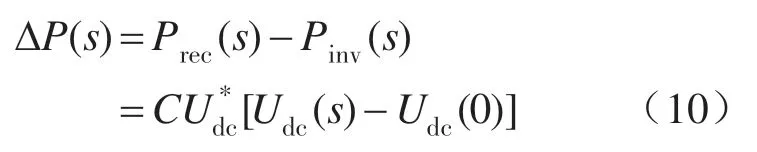
其中Udc(0)=化简上式可得：

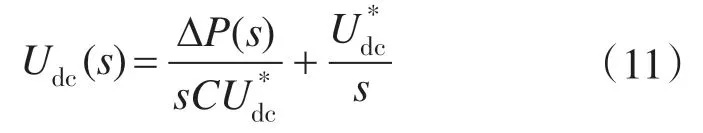
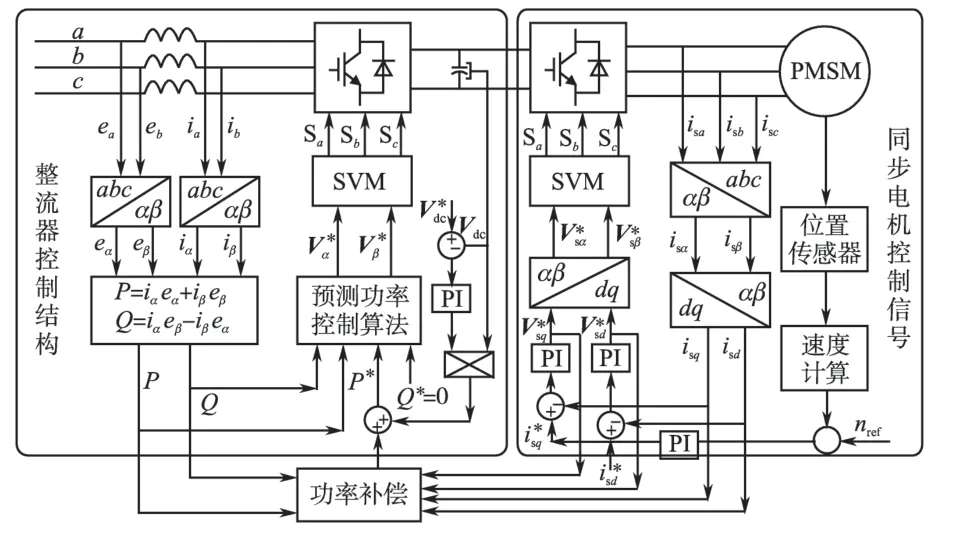
图2 双PWM变换器一体化控制框图Fig.2 Diagram of AC-DC-AC PWM converter control structure

由于无功功率不能通过整流桥，都体现在电容器的充放电过程，因而，PWM整流器有功功率指令可以表示为

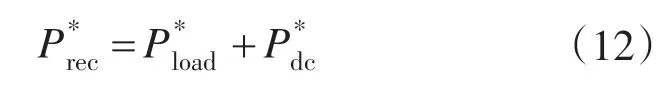
考虑采样延时，且直流电压环采用PI 调节器，将其视为一阶惯性环节，可得：

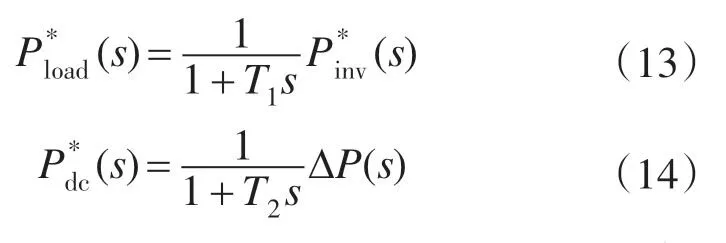
将指令值与实际值之间的延时等效为一阶惯性环节，可得：

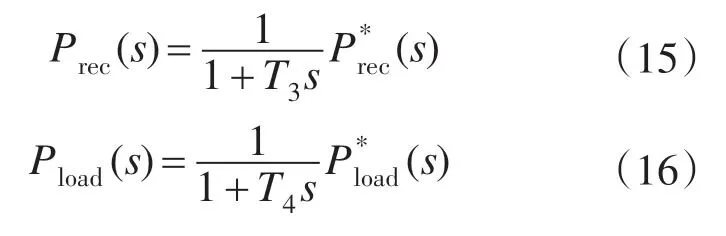
由式（9）～式（16）的功率关系可以得到双PWM变换器功率补偿的控制框图如图3所示。

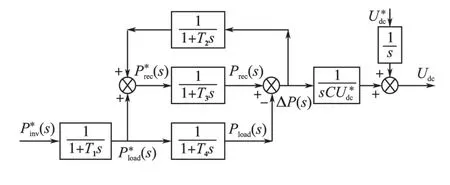
图3 双PWM变换器功率补偿控制框图Fig.3 Control structure diagram of AC-DC-AC PWM converter compensated with power

4 仿真分析及结论

本文提出的双PWM变换器协调控制策略在Matlab/Simulink环境下进行仿真，仿真时长0.25 s，三相交流电频率50 Hz，网侧开关频率5 kHz，直流侧电压Udc=800 V，直流侧电容470 μF，交流滤波电感L=3 mH；电机的基本参数为：调制频率10 kHz，极对数2，Ld＝0.008 5 H，Lq＝0.008 5 H，转动惯量0.000 8 kg·m2，定子磁阻0.002 875 Ω，摩擦系数0.001 N·m·s。

仿真过程1，给定负载转矩20 N·m，在0.2 s时电机转速给定值nref由800 r/min突变到1200 r/min。

图4～图6 分别为直流侧电压、网侧a 相电压电流波形、网侧整流器的有功和无功功率波形图，为方便观察，其中网侧a相电流放大15倍，电压缩小0.5倍。

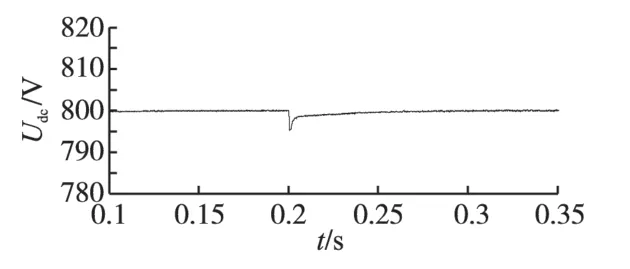
图4 直流侧电压波形Fig.4 Waveform for DC-link voltage

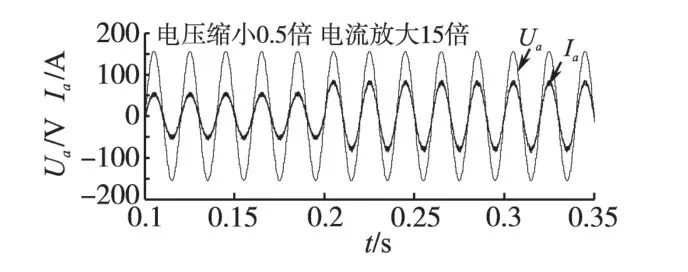
图5 网侧a相电压和电流波形Fig.5 Curves for AC current and voltage on axis a

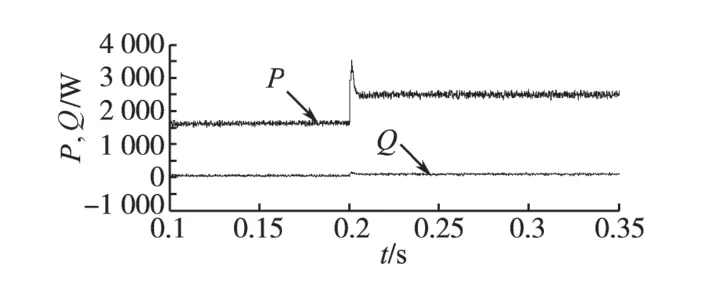
图6 整流器有功、无功功率波形Fig.6 Curves for active power and reactive power of converter

图7、图8 为直流侧电容在1 000 μF，网侧采用常规PI 控制，其他参数不变的情况下，直流侧电压和a相电压电流的波形图。

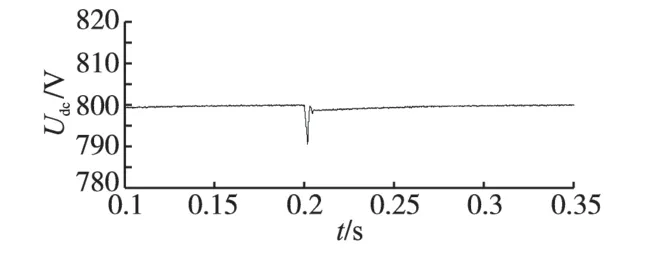
图7 常规PI控制下Udc的波形Fig.7 Curve of Udc under conventional PI control

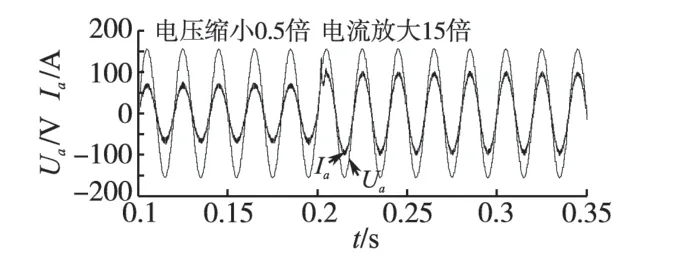
图8 常规PI控制下a相电压和电流波形Fig.8 Curves of Ua and Ia under conventional PI control

从仿真结果可以看出在网侧采用预测直接功率控制，并引入功率补偿，即使直流侧电容比较小，在负载突变的情况下，直流侧电压的波动很小，电压波动不到5 V，系统性能好。

仿真过程2，负转矩实验，给定转速800 r/min，直流侧电容470 μF，在0.25 s时负载转矩由20 N·m突变为-20 N·m。图9～图11为仿真过程2的仿真结果。

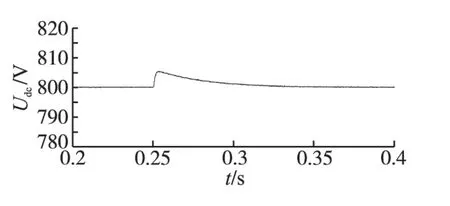
图9 负载突变下直流侧电压波形Fig.9 Curve for DC-link voltage when load change

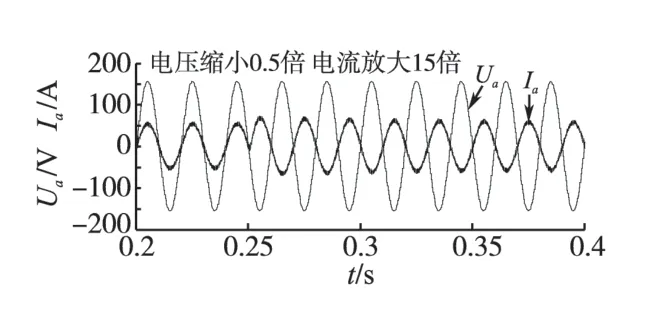
图10 负载突变下网侧a相电压电流波形Fig.10 Curves for ac current and voltage on axis a when load change

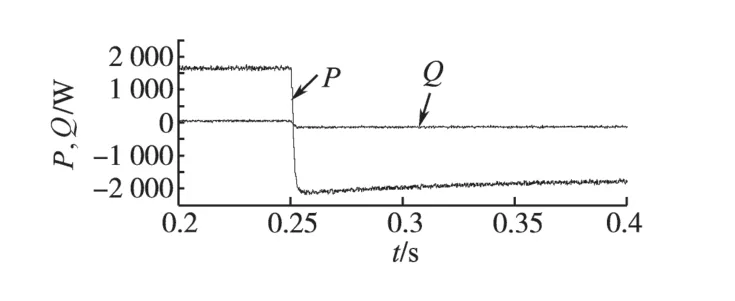
图11 负载突变下网侧有功和无功功率波形Fig.11 Curves for active power and reactive power when load change

从图9～图11 可以看出，永磁同步电机从电动运行突变到负转矩发电运行，在这一突变过程中，电压的波动也只有5 V，并很快就稳定下来。电动运行时，有功功率稳定在1 600 W左右，负转矩发电运行时有功功率稳定在-1 750 W左右，由于运行过程中电阻的一些损耗，电动运行与发电运行状态的功率有些许不同也属正常现象。

本文针对双PWM变换器提出了一种控制策略，网侧采用一种新型的基于直接功率控制的PWM预测控制策略，逆变器采用空间矢量控制，结合网侧与机侧的瞬时功率关系，将两者的功率信息补偿到网侧控制回路中，实现整流器对逆变器突变情况下的快速跟踪，大大降低了直流侧电压的波动，有效减小了直流侧电解电容的大小。与其它的双PWM 协调控制策略相比，本文提出的控制策略具有控制结构、方法简单，具有有效的可行性与实用性。

［1］张崇巍，张兴.PWM整流器及其控制［M］.北京：机械工业出版社，2012．

［2］Malesani L，Rossetto L，Tenti P,et al.AC/DC/AC PWM Converter with Reduced Energy Storage in the DC Link［J］. IEEE Tran.Industry Application，1995，31（2）：287-292.

［3］Gu Bon-Gwan，Kwanghee Nam.A DC-link Capacitor Minimization Method Through Direct Capacitor Current Control［J］.IEEE Tran.Industry Application，2006，42（3）：573-581.

［4］郑征，邹瑾，陶海军.双PWM 变频器一体化协调控制策略研究［J］.武汉大学学报：工学版，2011，44（3）：371-375.

［5］Hur NAMHO，Jung JINHWAN，Nam KWANGHEE. A Fast Dynamic DC-link Power-balancing Scheme for a PWM Converter-inverter System［J］. IEEE Transactions on Industrial Electronics，2001，48（4）：794-803．

［6］Lu Yin，Zhao Zhengming.An Improved DC-link Voltage Fast Control Scheme for a PWM Rectifier-inverter System［J］IEEE Tran.on Industry Applications，2014，50（1）：462-473.

［7］Noguchi T，Tomiki H，Kondo S，et al. Direct Power Control of PWM Converter Without Power-sorce Voltage Sensor［J］.IEEE Transactions on Industry Application，1998，34（6）：473-479.

［8］Bouafia A，Gaubert J P，Krim F. Predictive Direct Power Control of Three-phase Pulse Width Modulation（PWM）Rectifier Using Space-vector Modulation（SVM）［J］. IEEE Trans.on Power Electronics，2010，25（1）：228-236.

［9］李光叶.双PWM 变换器协调控制研究［D］.天津：天津大学，2011.

［10］杨兴武，姜建国. 电压型PWM 整流器预测直接功率控制［J］.中国电机工程学报，2011，31（3）：34-39.