单相高频隔离双向DC/AC变换器谐振控制

朱文杰，王慧，杨云虎，邱志鹏

（1.青岛理工大学自动化工程学院，山东青岛266520；2.河北科技大学电气工程学院，河北石家庄050018；3.安徽工业大学电气与信息工程学院，安徽马鞍山243032；4.国网济南供电公司，山东济南250012）

采用高频变压器隔离的HFL DC/AC 变换器相对于工频隔离的方案，具有体积小、重量轻、造价低、音频噪音小等优点［1］。双功率方向周波变换器类型的HFL 变换器［1-3］相比于单功率方向的HFL变换器，具有更灵活的运行方式和更强大的功能［4-5］，这也是本文所研究的控制对象。该类HFL变换器也引起国内外研究者的广泛关注，提出了许多调制方法和控制策略［6］，也取得了许多的研究成果。但对于HFL 变换器在连续时间域进行建模，并采用谐振控制器实现高性能控制和该控制器下的稳定性分析等方面的研究还未见有报导，需要进行探索。

本文中对电阻负载下双功率方向的周波变换器类型HFL DC/AC 变换器在连续时间域建立了数学模型，并根据此模型设计了针对此变换器输出电压控制的谐振控制器，然后对其进行了稳定性分析。最后通过实验结果证明了所设计谐振控制器对于该变换器输出电压控制的有效性。

1 HFL变换器电路及其调制策略

文中讨论的HFL 变换器电路如图1 所示，该电路有两级的功率变换，有利于转换效率的提升。在通常的应用中，需要从较低电压等级的直流侧电压E 升至较高电压的交流侧电压uo。变压器原边的全桥电路将输入的直流变换为高频的交流；副边周波变换将高频的交流转换为单极性的PWM 波形。通过后面的LC 滤波器，实现工频的交流电压输出。借助高频变压器的升压作用，在直流输入侧的母线大电容C的额定电压等级可以选得非常低，该电容的体积会很小，价格也比较低廉。钳位电路用来避免在周波变换器开断时高频变压器副边产生电压尖峰，并吸收由于漏感跟副边寄生电容上谐振而产生的电压振荡［4-5］。该变换器内部不需要大容量的直流电容，因而会提高系统可靠性。Lf和Cf分别是输出的滤波电感和滤波电容。N1是原边的匝数，N2和N3是副边的匝数，LK是归算到变压器原边的漏感。

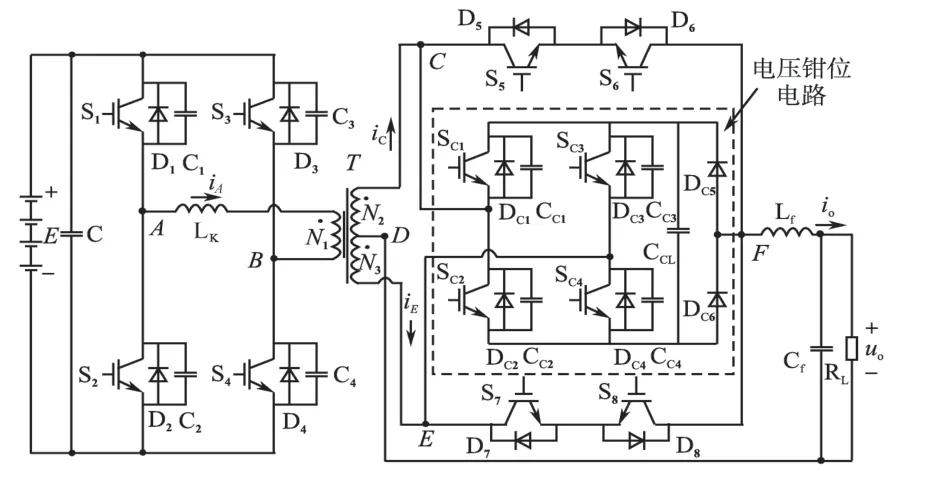
图1 周波变换器类型HFL DC/AC变换器Fig.1 Cycloconverter type HFL DC/AC converter

该逆变器的调制方法如图2 所示［4］。图3 绘制出在调制波ug>0时，该HFL变换器等效的调制过程。从图3中可推出uDF脉冲的宽度TA：

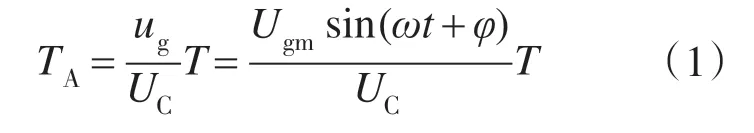
式中：φ为调制波ug的初相角。

可以看出逆变器输出电压uDF等效于一个单极性的PWM 调制。在输出电压的正半波区间uDF是正的脉冲，而在输出电压的负半波区间uDF是负脉冲。因为uDF脉冲的宽度与ug的绝对值成正比。如果调制波ug是一个正弦量，则输出电压uDF脉冲的宽度也随时间按照正弦量变化，可以等效为一个正弦的脉宽调制。

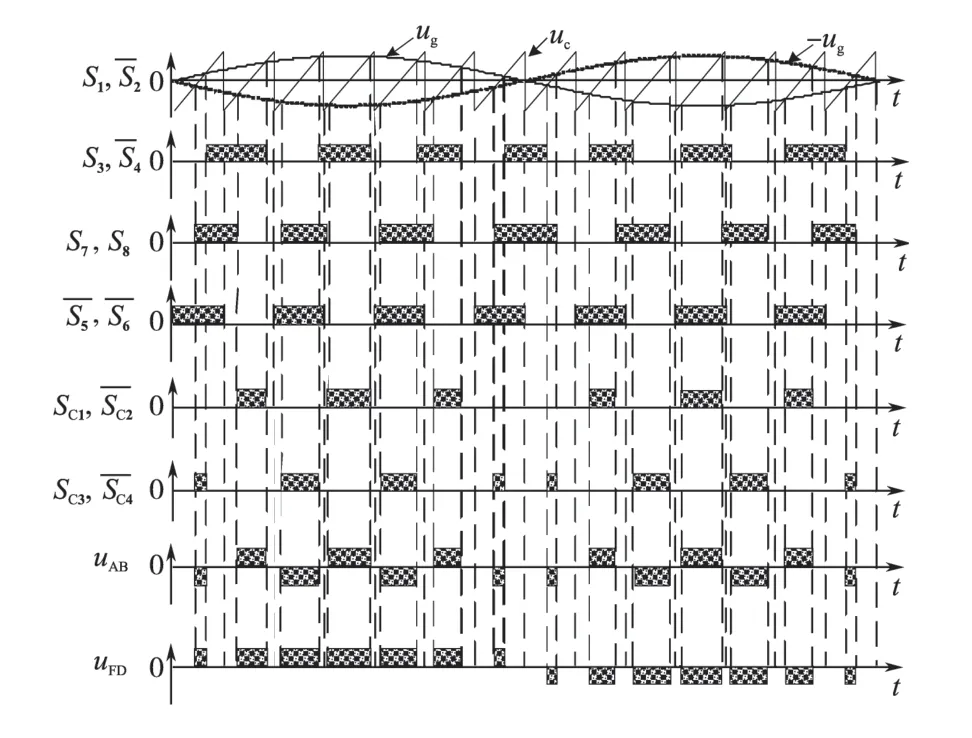
图2 HFL变换器的调制Fig.2 The modulation of HFL DC/AC converter

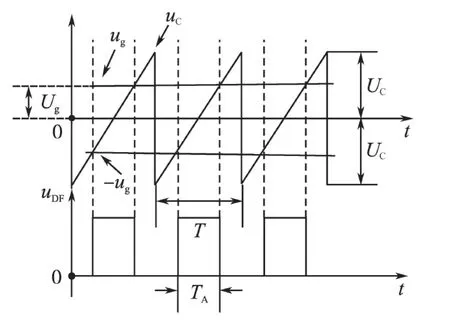
图3 调制过程的等效Fig.3 The equivalent modulation of the converter

2 HFL变换器的数学模型

从图2中可以推知，LC滤波器之前逆变器输出电压uDF可以写为

其中，n=N3/N1=N2/N1，当S=0 时，uDF=0；当S=1 时，uDF=nE；当S=-1时，uDF=uDF=-nE。

uDF在一个开关周期内的平均值为

式中：D为占空比，D=Ug/UC。

因此从如图2所示的调制器到逆变器输出的传递函数为

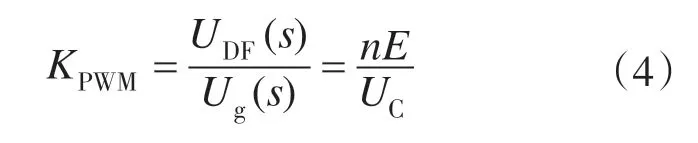
类似于两电平逆变器的建模方法［7］，忽略滤波电感中的串联电阻，可以得到该HFL变换器的连续时间域模型：

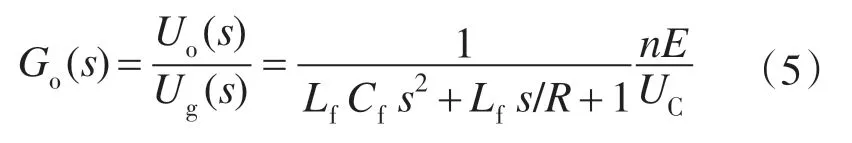
该变换器等效的方框图如图4所示。

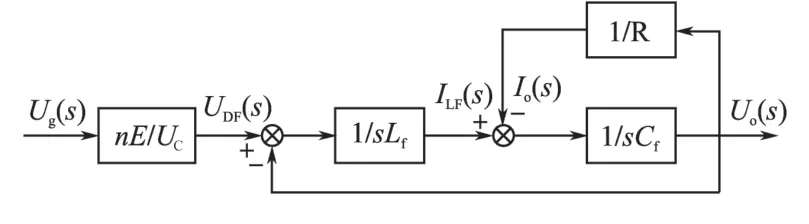
图4 HFL变换器等效框图Fig.4 The equivalent block diagram of the HFL converter

3 HFL变换器的数学模型

谐振控制适合于电阻负载的两电平逆变器控制，并得到了广泛的应用。谐振控制器具有结构简单，易于实现，鲁棒性好，收敛速度快等优点［8］。

3.1 HFL变换器的谐振控制

谐振控制可以在谐振频率处产生无穷大增益，从而使在该角频率ωn处的稳态误差为零。其传递函数为

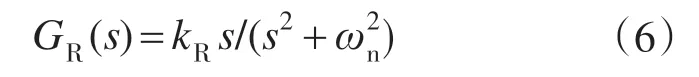
将其离散化后的结果为

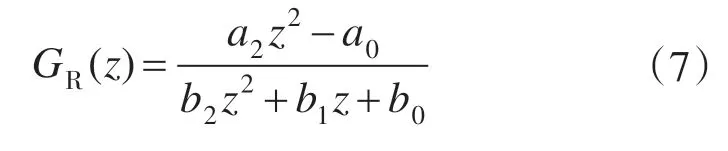
其中

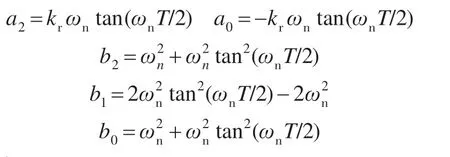
式中：T为采样周期。

采用谐振控制的HFL变换器控制框图如图5所示，图5中Uo为变换器输出交流电压，Uoref是控制系统的输出给定值。

图5 谐振控制的HFL变换器控制系统框图Fig.5 The block diagram of resonant controlled HFL converter system

本文中采用比例谐振控制器对变换器输出电压进行精确控制。利用比例谐振控制下的额定25 Ω阻性负载HFL变换器的波特图，留出适当的相位裕度，并兼顾误差收敛速度，取kR为8，比例控制器的系数为0.01。

3.2 稳定性分析

绘制出额定25 Ω负载和0.5 Ω负载时的波特图，分别见图6和图7。可以看出在额定负载下谐振控制器有88.3°的稳定裕度，在0.5 Ω负载时相角裕度只有34.5°，控制器稳定性已经变得很差。所以该控制器下稳定的负载变化范围为0.5Ω～∞。

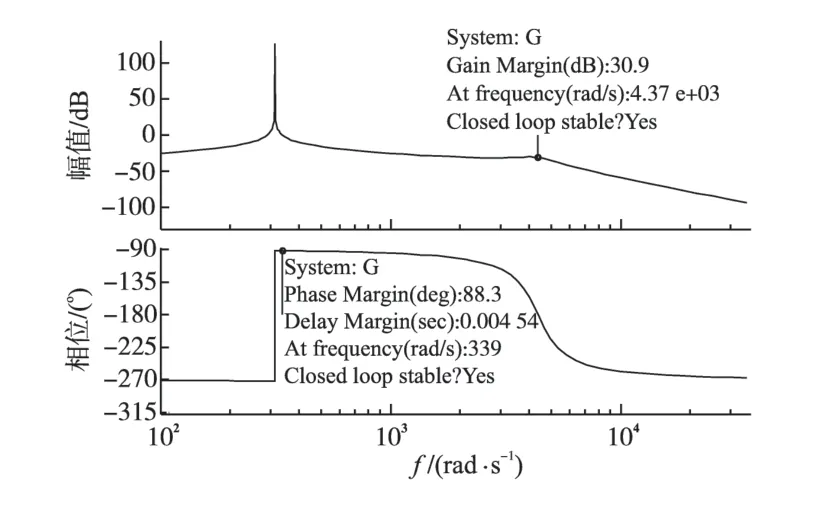
图6 负载为25 Ω时谐振控制HFL变换器波特图Fig.6 The bode diagram of the converter under 25 Ω load

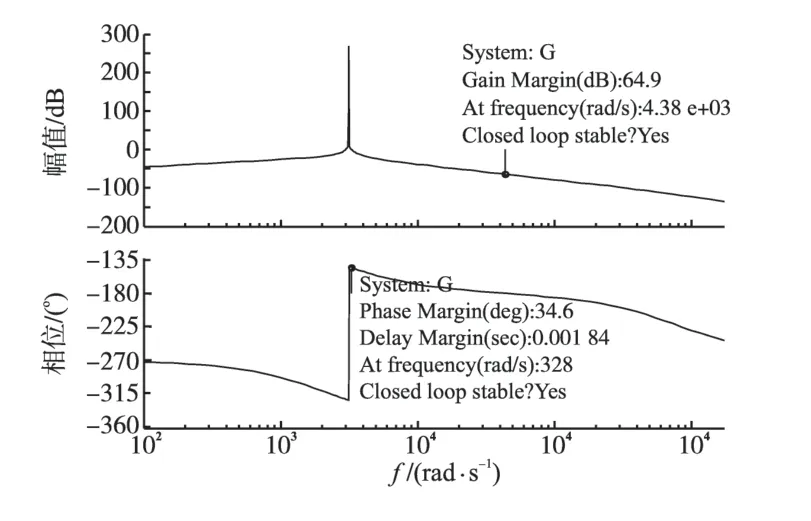
图7 负载为0.5 Ω时谐振控制HFL变换器波特图Fig.7 The bode diagram of the converter under 0.5 Ω load

4 实验验证

实验样机主要参数为，输入电压60 V，输出电压（峰值）100 V，变压器变比（升压）3，滤波电感Lf＝23.75μF，滤波电容Cf＝2 mH，变压器漏感3.16 μH。

控制算法和调制方法均由TMS320F28335实现，对输出电压实现了精确控制，开关频率采用20 kHz。并不需要外加另外诸如FPGA 之类的芯片实现调制，节省了成本。

4.1 HFL变换器中高频变压器主要波形

加入结合钳位电路的调制方法前后高频变压器副边N2上电压uCD和电流iC如图8 所示。在加入之前副边电压和电流有不同程度的过冲和振荡情况。可以看出在加入结合钳位电路的调制方法之后，完全避免了电压变压器副边电压产生过冲和振荡。

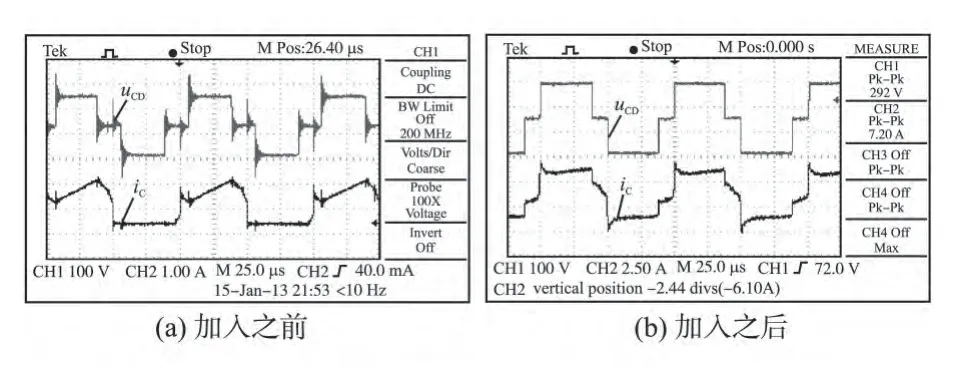
图8 高频变压器输出电压uCD和电流iC波形图Fig.8 Output voltage uCD and current iC of the transformer

4.2 HFL变换器的输出波形

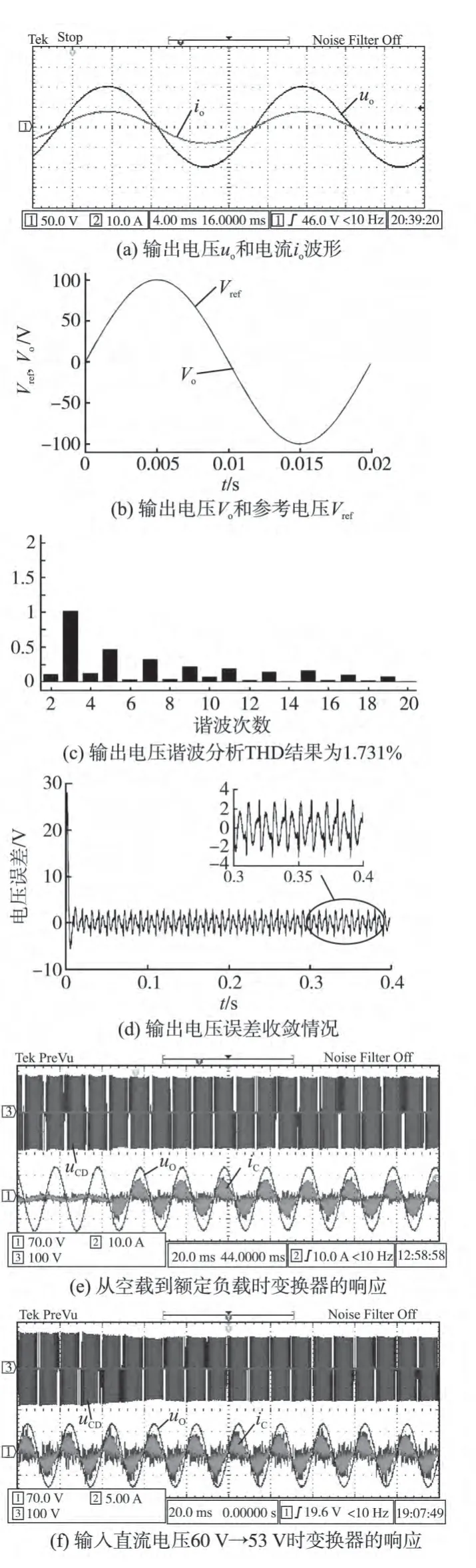
图9 输出实验波形Fig.9 Expaimental output waveforms

图9a 为稳态时该HFL 变换器输出的电压uo和电流io的波形，目测来看波形的正弦度高，线条很平滑。图9b 为参考电压和实际输出电压的波形图，两者基本重合，这说明稳态误差很小。图9c 为对输出电压uo的谐波分析，其谐波总畸变率（THD）为1.731%。图9d给出了开机之后输出电压误差的收敛情况，可以看出一个工频周期（20 ms）内输出就达到稳定，稳态误差的峰值为±3 V。图9e 给出了空载到额定负载变换器的中高频变压器输出电压uCD和输出电流iC的响应波形，在几个ms 内输出达到稳定值，且没有尖峰出现。图9f 给出了输入直流电压从60 V 变到53 V 时中高频变压器的输出，在几个ms内输出达到稳定值，且没有尖峰出现。另外在负载突变和输入直流电压变化时，输出电压uo都可以很快稳定到参考值。

5 结论

本文提出了周波变换器类型的HFL DC/AC变换器的连续时间域数学模型和适合该变换器的比例谐振控制器，并分析了在负载变化时的稳定范围。实验结果表明比例谐振控制器与结合钳位电路的调制方法相配合，避免了在变压器副边产生电压和电流波形的过冲和振荡，该变换器实现了对输出电压的精确快速控制，输出交流电压质量很好，在负载突变和输入电压变化等干扰出现的情况下也能迅速达到稳定输出，具有非常好的鲁棒性。

［1］陈道炼.高频环节电力电子变换技术的发展与现状［J］.电力电子技术，2014，48（6）：1-11.

［2］陈道炼，张友军.单极性移相控制高频脉冲交流环节逆变器研究［J］.中国电机工程学报，2003，23（4）：27-30.

［3］李磊，陈道炼，张友军，等.双极性移相控制高频脉冲交流环节逆变器研究［J］.电工技术学报，2003，17（6）：33-37.

［4］Zhu Wenjie，Zhou Keliang，Cheng Ming.A Bidirectional Highfrequency-link Single-phase Inverter：Modulation，Modeling，and Control［J］. IEEE Transactions on Power Electronics，2014，29（8）：4049-4057.

［5］Zhu Wenjie，Zhou Keliang，Cheng Ming，et al. A High-frequency-link Single-phase PWM Rectifier［J］. IEEE Trans.Ind.Electron.，2015，62（1）：289-298.

［6］Yamato I，Tokunaga N，Matsuda Y，et al. High Frequency Link DC-AC Converter for UPS with a New Voltage Clamper［C］// in Proc. 21th Annual IEEE Power Electronics Specialists Conference，1990：749-756.

［7］徐德鸿.电力电子系统建模与控制［M］.北京：机械工业出版社，2006.

［8］Zhou K，Wang D. Digital Repetitive Learning Controller for Three-phase CVCF PWM Inverter［J］.IEEE Trans.Ind.Electron，2001，48（4）：820-830.