三相4桥臂并网逆变器有源阻尼控制方法的研究

董钺，李钊，刘江华，邱晗，刘娜

（1.天津大学电气与自动化工程学院，天津300072；2.天津电气科学研究院有限公司，天津300180）

分布式可再生能源发电单元通常采用电压源型PWM 逆变器作为并网接口，并通过LCL 滤波器对输出电流的高频开关谐波进行抑制。与L滤波器相比，LCL 滤波器滤波效果更佳，且电感更小［1-2］。

文献［3］中提到，将并网电流反馈变为逆变器出口电流反馈，可以在电流闭环传递函数分母中引入3次项，起到阻尼作用，当滤波电感与并网电感比值在特定范围时可使电流稳定。文献［4-6］提到，在电流环内引入滤波电容电流或电容电压反馈，可以达到阻尼效果，文献［4］进一步指出，引入电容电流比例反馈等效于在滤波电容上并联电阻，若要更为精确地模拟滤波电容支路串联电阻的阻尼效果，需要在电容电流反馈中加入超前-滞后环节。文献［6］对数字控制中的采样计算滞后对有源阻尼效果的影响进行了分析，并指出LCL谐振频率高于某一频率后，只靠并网电流反馈同样可以实现电流稳定，但此时LCL的滤波效果已与L滤波类似。

本文以比例谐振控制并网电流的三相4桥臂并网逆变器为研究对象，首先对LCL滤波器参数进行合理选择［3，7］，而后在考虑采样计算滞后的基础上，提出一种改进型有源阻尼方法，即在并网电流环内，加入滤波电容电流负反馈，并将此反馈通过比例谐振环节后与并网电流控制器输出进行比例调节，并将此方法与文献［3-4］所提控制方法的异同进行比较，证明此方法兼顾了LCL滤波器的滤波效果与有源阻尼功能，最后，通过实验验证了该方法的有效性。

1 三相4 桥臂并网逆变器LCL 滤波器设计

由于并入380 V配网的分布式发电单元逆变器可带本地负载运行，而生活负载中单相负载占相当大的比重，为实现电流零序分量的灵活调节，逆变器可采用三相4桥臂结构。逆变器相关参数为：直流电压630 V，交流电压230 V，交流电流10.4 A，容量7 200 V·A，频率50 Hz，开关周期64 μs。

相对于基波电压电流，LCL滤波器可等效为单L，电感值为逆变电感与并网电感之和。为此，先确定此等效电感值。通常为提高直流电压利用率，三相逆变器采用空间矢量或载波加交流偏置的调制方式。在此种情况下，逆变器出口相电压峰值与直流电压之间的关系为

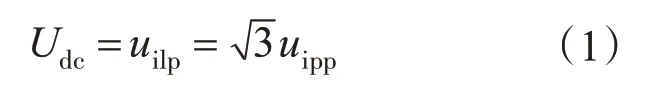
式中：Udc为逆变器直流电压；uilp为逆变器出口线电压峰值；uipp为逆变器出口相电压峰值。

根据逆变器电压电流与电网电压之间的关系，可知等效电感需满足下式要求：

式中：Lf为逆变滤波电感；Lg为并网电感；usp为电网相电压峰值；ifp为电感电流峰值。

将逆变器相关参数带入式（2），可得L ≤8 mH。考虑到逆变器需要输出无功、且电网电压允许±10%的波动，同时考虑直流电压调节裕度，L取为5 mH。

根据文献［7］，滤波电容无功容量不宜超过逆变器额定容量的5%，则可算出滤波电容值Cf为

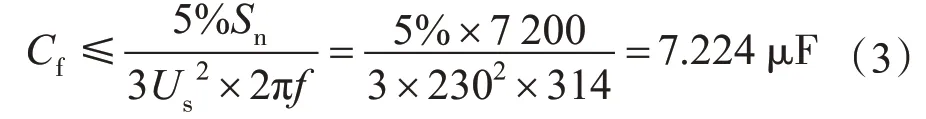
式中：Sn为逆变器额定容量；Us为电网相电压有效值。

然而，考虑到滤波效果，Cf取为10 μF，此时的基波电容电流为额定电流的6.94%，在额定容量时对应的有功电流分量为额定电流的99.76%，即使逆变器无功功率或功率因数开环，其对稳态功率因数的影响仍在可以接受的范围内（＜1%）。

为限制逆变器出口电流脉动在10%以下，可得滤波电感Lf［7］为

式中：T为开关周期；Δifmax为逆变出口电流脉动上限值。

考虑抑制电网电压波动对并网电感电流的影响，并网电感值不应过小，因此并网电感值取为1 mH，逆变滤波电感值取为4 mH。可计算出LCL滤波器谐振频率为

此谐振频率在10倍基波频率（500 Hz）和0.5倍开关频率（7 812 Hz）之间，且满足设计要求。

2 有源阻尼数学模型分析

由于电能质量要求的指标都是针对逆变器入网电流而言的，因此，对逆变器入网电流进行闭环调节最为简单直接。尤其是在对逆变器输出的无功功率进行调节时，采用入网电流反馈可以消除滤波电容电流对稳态精度的影响。此外，为在电流调节器中省去矢量变换与反变换，同时可以对电流给定进行稳态无差跟踪，电流环采用比例谐振控制。同时，为消除电网电压波动与畸变对逆变器入网电流的影响，引入电网电压直接前馈。在这种情况下，控制框图如图1所示。

图1 比例谐振电流环传递函数Fig.1 Transfer function of PR current loop

由图1 可知，LCL 滤波器的传递函数存在谐振点，谐振频率即为fres。而针对基波的比例谐振控制器不能抑制此谐振。

2.1 连续模型分析

在此电流环内引入滤波电容电流比例反馈，可以抑制谐振［4-6］。此时的传递函数如图2所示。

图2 滤波电容电流比例反馈传递函数Fig.2 Filter transfer function with capacitor current proportional feedback

由图2可知，引入滤波电容电流比例反馈后，LCL滤波器传递函数的分母中加入了kLgCfs2项，起到了阻尼作用。

然而，在实际的数字控制中，采样与控制存在至少一个控制周期的滞后。文献［4，6］指出，该滞后会削弱有源阻尼的谐振抑制作用，甚至引起电流的不稳定。由于采用滤波电容电流比例反馈的有源阻尼方法，等效于在滤波电容上并联阻尼电阻［4］，而并联电阻的阻尼效果不如在电容支路上串联电阻［7］，因为二者的传递函数分母相同而分子不同，后者分子上存在1次项。

为达到与在滤波电容支路串联电阻等效的效果，需要在滤波电容电流反馈回路中加入其他环节。由图2 可知，若要LCL 滤波器传递函数除分母中的阻尼项外、分子上同时出现1 次项，需要在电容电流反馈通道中引入惯性环节。引入惯性环节后，LCL 滤波器传递函数如图3所示。

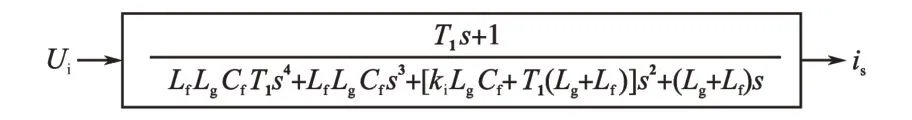
图3 滤波电容电流惯性反馈传递函数Fig.3 Filter transfer function with capacitor current inertial feedback

图3中，T1为惯性环节时间常数，ki为惯性环节增益。由图3 可以看出，滤波电容电流反馈通路中引入惯性环节，除在传递函数分子上引入1次项外，还在分母中加入4次项。由于T1较小，而该项次数较高，因此4次项可以忽略。

由于滤波电容电流中的谐振分量频率较高，为提高带宽，在反馈通道中引入惯性环节的同时也要叠加比例环节，传递函数如图4所示。

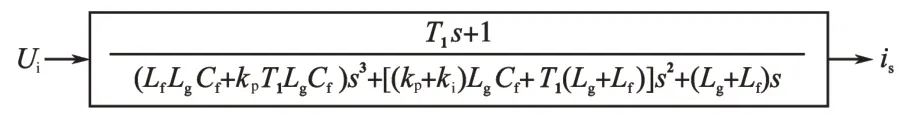
图4 滤波电容电流比例—惯性反馈传递函数Fig.4 Transfer function with capacitor current proportional-inertial feedback

2.2 离散模型分析

由于逆变器采用数字控制，同时，需要考虑采样与控制存在的滞后对稳定性的影响，因此，需要对电流控制器和LCL 滤波器的模型进行离散化。离散化后的控制框图如图5所示。

图5 中，Gc(z)为电流控制器离散模型，Gf(z)为滤波电容电流反馈环节离散模型，G1(z)为逆变电压到滤波电容电流环节离散模型，G2(z)为滤波电容电流到入网电流环节离散模型，z-1Vdc表示将电流控制器滞后及滤波电容电流采样滞后考虑在内的逆变器模型，Vdc即为逆变器直流电压。

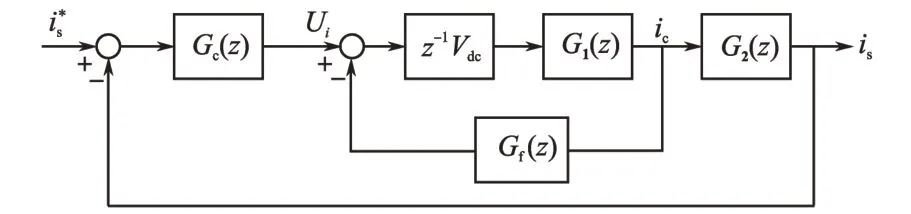
图5 加入有源阻尼后电流环离散传递函数Fig.5 Discrete current loop transfer function with active damping

首先对电流控制器进行离散化，由于电流调节采用比例谐振控制，传递函数如图1中所示，将其离散化可得：

式中：T为采样与控制周期。

逆变电压到滤波电容电流的连续传递函数如图2a中所示，将其离散化可得：

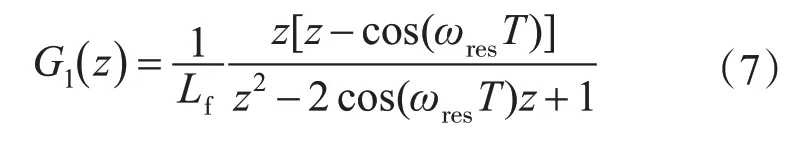
式中：ωres为LCL滤波器谐振角频率。

滤波电容电流到入网电流的连续传递函数亦如图2a中所示，将其离散化可得：

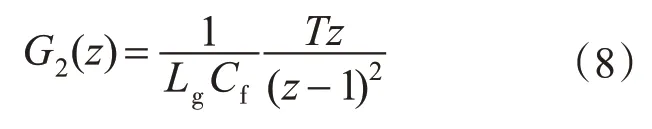
滤波电容电流反馈环节若为比例—惯性环节，则其连续传递函数为kp+ki/(T1s+1)，将其离散化，可得：

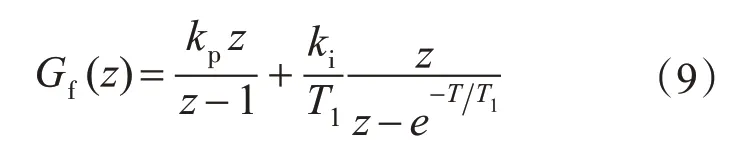
在不考虑数字控制与采样滞后的情况下（即图5 中z-1Vdc由Vdc替代），引入滤波电流比例反馈时电流调节器输出Ui到滤波电容电流ic的传递函数的根轨迹与伯德图如图6所示。

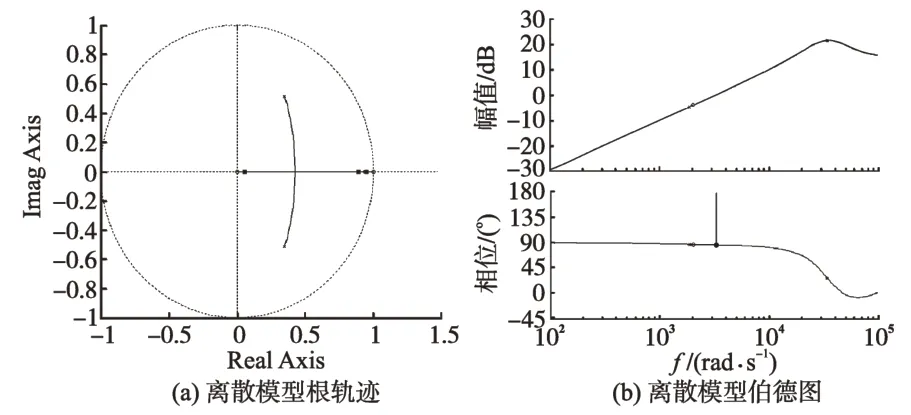
图6 不考虑滞后的离散模型根轨迹与伯德图Fig.6 Root locus and bode diagram of discrete model without sample delay

由图6可见，根轨迹落在单位圆内，相角裕度为正，传递函数稳定。

在考虑数字控制与采样滞后的情况下，引入滤波电流比例反馈时电流调节器输出Ui到滤波电容电流ic的传递函数的根轨迹与伯德图如图7所示。

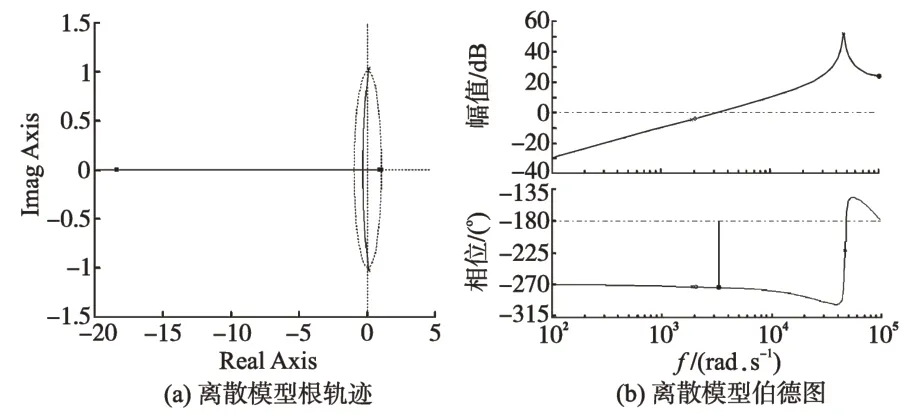
图7 考虑滞后的离散模型根轨迹与伯德图Fig.7 Root locus and bode diagram of discrete model with sample delay

由图7可见，一部分根轨迹落在单位圆外，且相角裕度为负，故而，在考虑控制与采样滞后的情况下，离散传递函数不稳定。

因此，为解决数字控制与采样滞后的问题，在电流反馈环节中加入比例—惯性环节，并将此反馈环节与电流调节器输出做比例调节，改进后的控制结构如图8所示，其中，k为比例调节系数。

图8 改进后的有源阻尼电流环离散传递函数Fig.8 Discrete current loop transfer function with improved active damping

在考虑数字控制与采样滞后的情况下，Ui到ic的离散传递函数的根轨迹与伯德图如图9所示。

图9 改进有源阻尼离散模型的根轨迹与伯德图Fig.9 Root locus and bode diagram of discrete model with improved active damping

由图9 可见，可以通过调节电容电流反馈环节和比例环节系数，使系统达到稳定。

由于逆变器交流侧各变量为正弦量，在电容电流反馈通道中，与惯性环节相对应的正弦“惯性”环节，为二阶带通滤波器，因此滤波电容电流反馈通道的离散传递函数如下式所示：

如上所述，本文采用的滤波电容电流比例—惯性反馈的有源阻尼控制方法，其结构如图10所示。

图10 改进后的有源阻尼控制结构Fig.10 Improved active damping control structure

2.3 与逆变器出口电流反馈的异同

文献［3］提出，用逆变器出口电流反馈可以起到有源阻尼的作用，其采用比例谐振电流调节器的控制结构如图11所示。

图11 逆变器出口电流反馈控制结构Fig.11 Control structure of inverter output current feedback

此时，逆变器调制信号可表示为

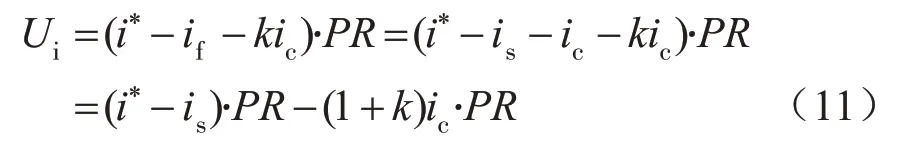
由式（11）可得逆变器出口电流反馈控制的等效控制结构如图12所示。

图12 逆变器出口电流反馈等效控制结构Fig.12 Equivalent control structure of inverter output current feedback

对比图10 与图12 可知，逆变器出口电流反馈的控制结构与本文提出的控制结构相同，只是电容电流反馈通道的系数与电流调节器系数成相同比例、电容电流反馈与电流调节器输出的比例系数为1，可以视作本文所提控制结构的特例。

3 试验波形

下面分别对常见的滤波电容电流比例反馈的控制方法与本文提出的改进型有源阻尼控制方法进行试验，并将二者的波形进行对比。逆变器参数同第1节。

由于逆变器LCL滤波器的谐振频率为1 780 Hz，接近36 次谐波，因此逆变器入网电流中35，37 次谐波含量可以作为有源阻尼有效性的判定依据。

图13为采用常见的滤波电容电流比例反馈、功率为2 kW 时的电网电压和入网电流波形，以及相应的电流畸变率。图14 为采用滤波电容电流比例反馈、功率为7.2 kW时的电网电压和入网电流波形，以及相应的电流畸变率。图15为采用改进型有源阻尼控制方法、功率为2 kW 时的电网电压和入网电流波形，以及相应的电流畸变率。图16为采用改进型有源阻尼控制方法、功率为7.2 kW时的电网电压和入网电流波形，以及相应的电流畸变率。

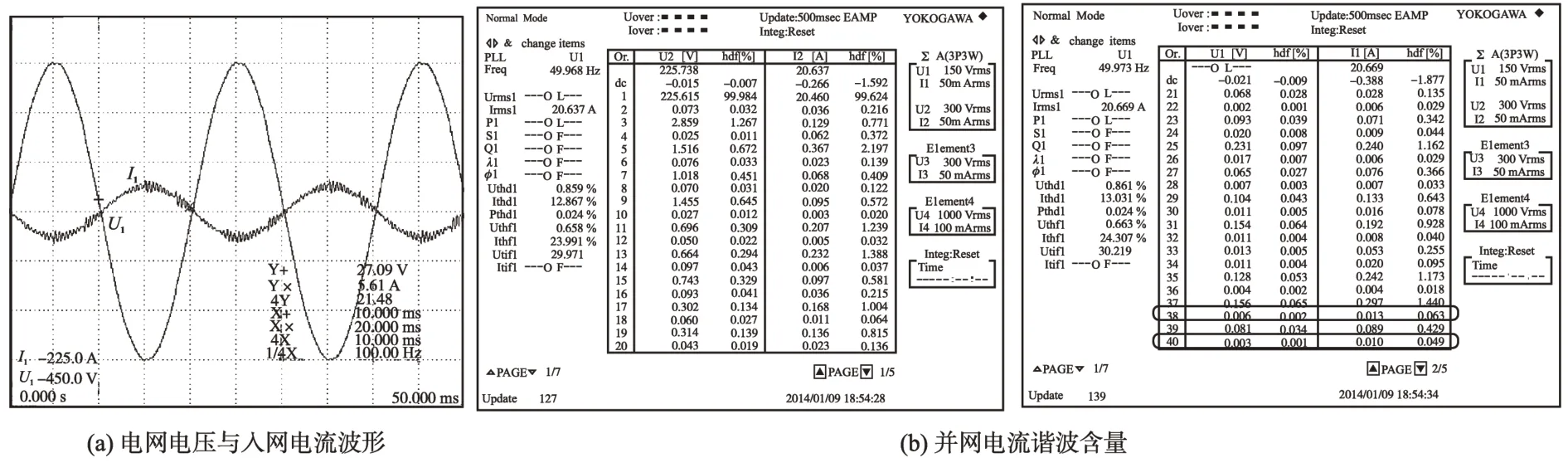
图13 2 kW时滤波电容电流比例反馈的波形Fig.13 Waveforms with filter capacitor current proportional feedback when the power is 2 kW

图14 7.2 kW时滤波电容电流比例反馈的波形Fig.14 Waveforms with capacitor current proportional feedback when the power is 7.2 kW

图15 2 kW时采用改进型有源阻尼的波形Fig.15 Waveforms with improved active damping method when the power is 2 kW

表1 为采用不同有源阻尼方法时的谐波含量及电流总畸变率对比。

由表1可知本文所提的改进型有源阻尼算法可以更好地抑制谐振，降低电流的波形总畸变率。

图16 7.2 kW时采用改进型有源阻尼的波形Fig.16 Waveforms with improved active damping method when the power is 7.2 kW

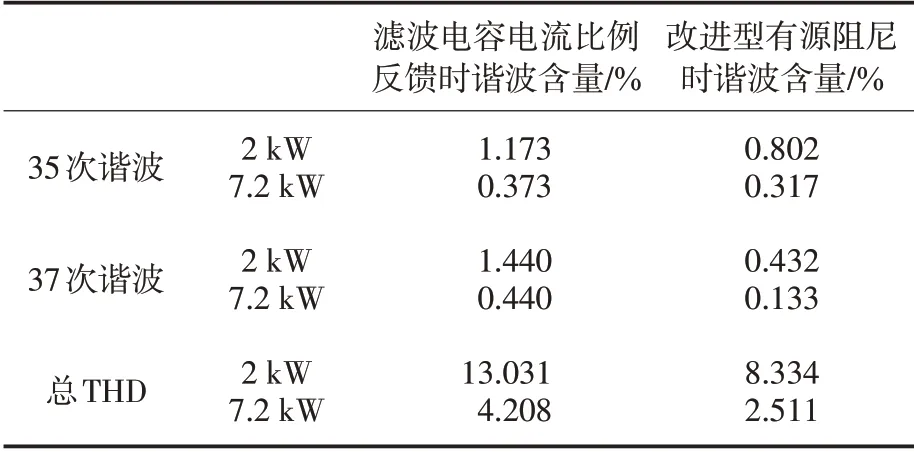
表1 不同有源阻尼方法谐波含量Tab.1 Grid current harmonic content of different active damping method

4 结论

本文首先对逆变器LCL 滤波器参数进行设计，进而在常见的采用滤波电容电流反馈的有源阻尼方法的基础上，建立LCL滤波器离散数学模型，提出一种改进型有源阻尼控制方法，可以有效地避免数字控制与采样滞后对有源阻尼效果的影响，并与逆变器出口电流反馈的方法进行对比，最后通过根轨迹、伯德图和实验波形验证了该方法的有效性。

［1］Teodorescu R，Blaabjerg F，Liserre M，et al.A Stable Threephase LCL-filter Based Active Rectifier Without Damping［C］//in Conf. Rec. IEEE IAS Annu. Meeting，Salt Lake City，UT，USA，2003：1552-1557.

［2］Dannehl J，Wessels C，Fuchs F W.Limitations of Voltage-oriented PI Current Control of Grid-connected PWM Rectifiers with LCL Filters［J］.IEEE Trans.Ind.Electron.，2009，56（2）：380-388.

［3］Yi Tang，Poh Chiang Loh，Peng Wang，et al.Exploring Inherent Damping Characteristic of LCL Filters for Three-phase Grid Connected Voltage Source Inverters［J］. in IEEE Transactions on Power Electronics，2012，27（3）：1433-1443.

［4］Lei Yi，Zhao Zhengming，He Fanbo，et al.An Improved Virtual Resistance Damping Method for Grid Connected Inverters with LCL Filters［J］. IEEE Energy Conversion Congress and Exposition（ECCE），17-22 Sept.2011：3816-3822.

［5］Jörg Dannehl，Friedrich Wilhelm Fuchs，Steffan Hansen，et al. Investigation of Active Damping Approaches for PI-based Current Control of Grid Connected Pulse Width Modulation Converters with LCL Filters［J］. in IEEE Transaction on Industry Applications，July/August 2010，46（4）：1509-1517.

［6］Stewart Geoffrey Parker，Brendan P McGrath，Donald Grahame Holmes.Regions of Active Damping Control for LCL Filters［J］.in IEEE Transactions on Industry Applications.January/February 2014，50（1）：424-432.

［7］张兴，曹仁贤.太阳能光伏并网发电及其逆变控制［M］.北京：机械工业出版社，2010.