基于相关向量机的加速度计参数变化规律研究

杨继红，于湘涛，付秀娟，于 皓，韩 旭，龚锦莉

（1.海军驻某院军事代表室，北京 100074;2.北京自动化控制设备研究所，北京 100074）

在已知超先验情况下，对p（t|α，σ2）取最大值

0 引言

惯性导航是一门涉及多学科的综合性技术，是实现运动体自主式控制和测量的最佳途径，广泛应用于航天、航空、航海等领域［1］，石英挠性加速度计 （以下简称加速度计）作为惯性导航系统最重要的器件之一，其测量精度高低直接影响惯性系统的精度［2］。加速度计受温度等环境载荷以及其内部构件材料的特性的影响，加速度计参数随时间会发生漂移，从而导致加速度计的输出发生变化［3］，因此，进行加速度计参数变化规律的研究对于提高惯性导航系统的精度具有重要意义。

相关 向 量机［4］（Relevance Vector Machine，RVM）是 Tipping提出的一种与支持向量机［5］（Support Vector Machine，SVM）形式相同的稀疏概率模型，其训练是在贝叶斯框架下进行的，通过超参数给出权值的先验概率，并通过迭代算法求出最优值，在实际预测性能相当的情况下，解的稀疏性明显高于SVM。

基于RVM的优点，建立了加速度计参数RVM预测模型，为了验证所提方法的有效性，针对2.5年自然贮存的加速度计参数标定值，应用RVM和最小二乘法分别进行了加速度计参数建模，计算结果表明RVM建模效果更优。

1 模型预测算法

时间序列预测［6］是指利用历史数据构建时间序列模型，依据所建模型进行外推预测未来。统计学方法是时间序列预测的主要方法，常见的时间序列分析方法包括:自回归滑动平均模型 （Autoregressive Moving Average，ARMA）等，基于机器学习理论发展起来的人工神经网络和支持向量算法等智能预测方法具有自适应、自学习机制，可以对非线性时间序列进行更准确地预测。

1.1 ARMA模型试验时间预测方法

ARMA模型时间序列分析法简称为时序分析法，是一种利用参数模型对有序随机数据进行处理，从而进行参数预测的方法，参数模型包括AR自回归模型、MA滑动平均模型和ARMA自回归滑动平均模型，ARMA时间序列具有遍历性。

式 （1）的左边称为自回归差分多项式，即AR模型，右边称为滑动平均差分多项式，即MA模型，p、q为自回归模型和滑动均值模型的阶次，ak、bk分别表示待识别的自回归系数和滑动均值系数，y表示白噪声激励。

确定ARMA模型的阶数，即p和q的数值的求解可以通过 AIC（Akaike Information Criterion，AIC）法、F检验法等方法求解，自回归系数可以通过建立Yule-walker方程，采用伪逆法可求得方程组的最小二乘解，滑动平均模型MA系数的估算方法很多，主要的有基于Newton-Raphson算法的迭代最优化方法和基于最小二乘原理的次最优化方法。

1.2 相关向量机算法

相关向量机是Tipping提出的一种贝叶斯框架下的稀疏概率机器学习模型，假设一系列输入向量 x={xn，n=1，2，．．．，N}和相应的输出 y={yn，n=1，2，．．．，N}， 设计的模型对于新的输入xn，预测出输出y（xn），所观测的输出tn，它可以看作未知函数y（x，w），该函数包含方差为σ2的高斯噪声。

式中，ε是噪声信号，且是独立分布的，w是可调参数权值，其中Φi（x）=K（x，xi），这里的核函数的选择不受Mercer定理的限制。相应的训练样本集的似然函数为

采用稀疏贝叶斯方法对权值w赋予先验的条件概率分布

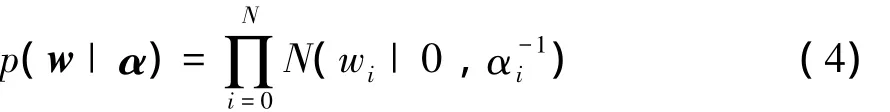
式中，α是决定权值先验分布的超参数，根据贝叶斯公式可以得到

在已知超先验情况下，对p（t|α，σ2）取最大值

由于不能直接获得式 （6）中α和σ的解析表达式，因此，使用迭代公式进行估计。

式中，γi=1－αiNii，Nii为后验权协方差矩阵的第i个对角元素。

若给定一个输入值x*，则可通过下面几步实现新的预测。

RVM对新观测值的预测输出为y（x*;μ）。

2 加速度计参数变化规律

2.1 加速度计参数变化原因分析

1）胶粘剂材料稳定性:在加速度计关键的部组件——磁钢与激励环、动圈与石英摆片等位置采用胶粘剂连接，胶粘剂在长期环境载荷作用下会发生蠕变，蠕变是通过分子链段的逐渐伸展或相对滑移实现的，结果不仅会造成力学松弛，还会使得被粘接的构件发生相对位移，胶粘剂材料的稳定性使得敏感质量的质心和电磁力的力心变化，使得加速度计参数长期重复性发生变化。

进行了胶粘剂变化导致动圈沿着摆轴移动与力矩器电磁力之间的仿真，仿真结果如图1所示。

图1 电磁力与动圈移动之间的关系示意图Fig.1 The relationship between electro-magnetic force and the force coils movement

从图1中可以看出线圈所受合力随线圈沿摆轴的正负偏移量增大而增大，但是在相同偏移量的情况下，远离挠性平桥的偏移对电磁力的影响更大。

2）永磁材料稳定性:加速度计力矩器在输入信号作用下产生反馈力矩以平衡外界的惯性力矩，磁性能的稳定性直接影响力矩器的稳定性，磁时效是永磁材料磁性能随时间的一种不可逆连续变化，是由于材料内部的结构调整所引起的，为了解释磁时效现象，许多科学家进行了研究，并建立了理论模型。

进行了不同的磁钢磁感应强度退化时的仿真，其中退化1%时，磁路云图如图2所示。

图2 加速度计磁路矢量图Fig.2 The vector graph of accelerometer magnetic circuit

仿真结果表明磁钢退磁1%时，标度因数增大约7‰。

3）金属构件尺寸的稳定性:材料的相与组织状态的不稳定性及在各种热加工与冷加工工艺过程中，零件中发生的残余应力的松弛导致金属制件尺寸变化，也是引起加速度计参数变化的因素之一。

2.2 加速度计长期重复性测试方案

为了评估加速度计参数变化规律，进行了加速度计长期重复性试验设计，标定周期0.5年，总共2.5年，测试样本18块，将加速度计按“门状态”安装，如图3所示。

“门状态”即分度头置于0°时，加速度计输入基准轴 （IA）与水平面的夹角满足技术要求，摆基准轴 （PA）平行于旋转轴，输出基准轴 （OA）垂直向下，当分度头旋转至90°时，输入基准轴正方向垂直向上，按照GJB1037A［7］进行四点翻滚试验标定加速度计的偏值和标度因数。

图3 “门态”试验安装图 （分度头0°）Fig.3 The chart of the hinge axis

2.3 加速度计数据规律分析

加速度计参数RVM建模步骤:

图4 基于最小二乘法的加速度计参数建模示意图Fig.4 The modeling result of accelerometer based on least squares method

1）收集整理加速度计标定数据序列，Xn={x1，x2，…，xN}，xi∈ R，i=1，2，…，N;

2）对原始序列XN进行归一化处理;

4）对样本进行RVM预测。

应用最小二乘法和RVM建立了加速度计参数模型，模型曲线如图4和图5所示。

从图4和图5可以看出，二阶回归模型和

图5 基于RVM的加速度计参数建模示意图Fig.5 The modeling result of accelerometer based on RVM

3）选择RVM核函数，常用的几种核函数有RBF核函数、线性核函数、多项式核函数等。其中，RBF核函数具有较好的学习能力，选用RBF函数作为RVM的核函数，其数学表达式为RVM模型都可以用来加速度计参数变化建模，当加速度计参数变化存在非线性时，二阶模型回归与实际参数变化存在较大误差，而RVM可以很好地给出加速度计参数变化结果。

3 结论

受温度、振动等环境载荷的影响，加速度计参数随着时间会发生变化，基于RVM具有稀疏的模型适合时间序列预测的优点，提出了一种加速度计参数预测方法，用RVM和最小二乘法分别建立了加速度计参数模型，计算结果表明RVM的建模效果更优。

［1］郑辛，杨林．导航、定位与授时技术综述［J］．导航定位与授时，2014，1（1）:1-7．

［2］顾英．惯导加速度计技术综述［J］．飞航导弹，2001，（6）:78-85．

［3］于湘涛，张菁华，杜祖良．石英挠性加速度计参数长期重复性技术研究［J］．导航定位与授时，2014，1（1）:58-62．

［4］Tipping M E．Sparse Bayesian learning and the relevance vector machine［J］．Journal of Machine Learning Research，2001，l（3）:211-244．

［5］Vapnik V N．An overview of statistical learning theory［J］．IEEE Transactions on Neural Networks，1999，10（5）:988-1000．

［6］张美英，何杰．时间序列预测模型研究综述［J］．数学的实践与认识，2011，41（18）:189-195．

［7］GJB 1037A，单轴摆式伺服线加速度计试验方法［S］．2004．