组合导航系统状态切换对末段导引的影响分析及措施研究

姜易阳，洪诗权，宋 闯

（北京机电工程研究所，北京 100074）

0 引言

固定点攻击又称坐标攻击，是精确打击时常用的一类攻击模式，主要针对坐标精确已知的地面目标，或无地面特征的地下目标。在该攻击模式下，多采用惯性/卫星组合导航系统提供精确的飞行器位置，实现对目标的有效打击［1-2］。

然而实际飞行过程中，由于末段大角度俯冲、PDOP值不满足定位要求等因素［3］，卫星接收机并不能保证全程定位，组合导航系统可能长时间处于纯惯性导航状态。一旦接收机定位，由于纯惯性导航带来的误差累积，组合导航系统状态切换导致其输出的飞行器位置信息出现跳变，会对制导控制带来不利影响，甚至导致飞行弹道异常。目前对组合导航系统的研究多集中在组合滤波算法［4-5］、多传感器组合下的数据融合技术［6-7］、故障检测算法［8］等方面，而该方面的研究鲜有公开报道。

本文系统地分析了惯导状态切换对末段导引的影响。在此基础上，提出了不同的解决方案，并分别进行了蒙特卡洛仿真。分析统计结果表明，自适应更改预定落角的改进方案可适应不同的纯惯性导航误差，并降低了对弹道落角的影响。

1 制导控制系统方案

某飞行器的典型飞行弹道如图1所示［9］，其中，0＜t＜t1为姿态稳定段，t1≤t＜t2为爬升段，t2≤t＜t3为转弯段，t3≤t为末导引段。

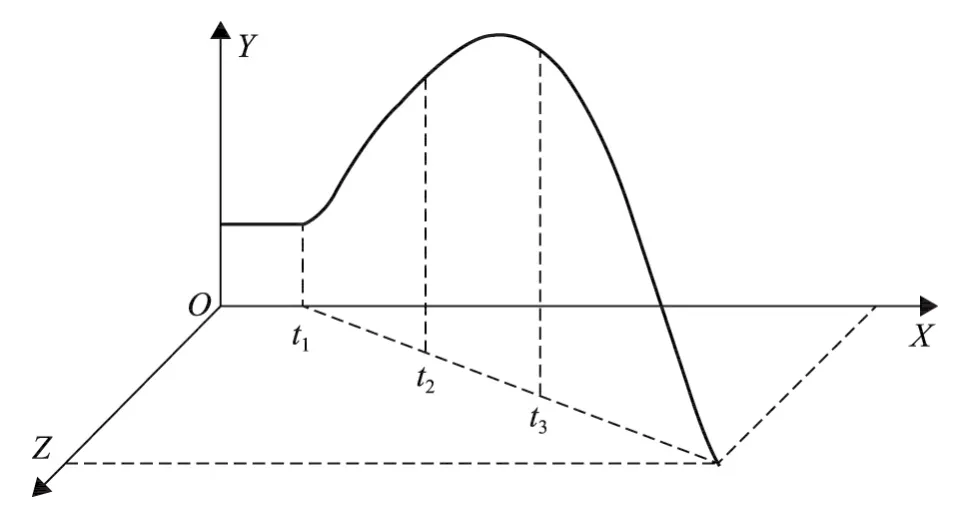
图1 典型飞行弹道示意图Fig.1 The scheme of flight trajectory

对于固定点攻击模式，采用惯性/卫星组合导航的制导体制，导引信息由装订的目标位置坐标（Xt、Yt、Zt）和组合导航系统输出的飞行器位置坐标 （Xn、Yn、Zn）解算得到，以进行虚拟导引［10］。为增强战斗部毁伤效果，末导引段采用带落角约束的制导律［11］，实现大落角攻击。

2 组合导航系统状态切换影响分析

2.1 仿真模型简述

为研究组合导航系统状态切换对末段导引飞行的影响，针对典型弹道进行蒙特卡洛仿真分析。仿真中组合导航系统模型进行如下设置:在飞行器发射后的飞行初段，设置组合导航系统处于纯惯性导航状态，并根据惯性导航误差方程计算纯惯性导航误差，组合导航系统输出的飞行器空间位置坐标中存在误差，且随着飞行时间的增长，惯性导航位置误差不断加大;经一定飞行时间后，设置惯导处于组合导航状态，即组合导航系统进行了状态切换，此时纯惯性导航误差被消除，组合导航系统输出飞行器的实际空间位置坐标。因该状态切换时间很短，在数学仿真时可忽略状态切换时的过渡过程，即组合导航系统的输出在状态切换时存在跳变，且输出跳变的幅值随着纯惯性导航误差的增大而增大。

为研究惯导状态切换时刻对飞行弹道的影响，在进行蒙特卡洛仿真时，设置不同的状态切换时间点，对于各状态切换点，均采用蒙特卡洛仿真的方式对脱靶量进行统计。

同时，仿真时考虑的飞行器气动力系数（即Cx、Cy、Cz）和气动力矩系数（即 Mx、My、Mz）的计算及拉偏模型如式 （1）～式 （6）:

其中，α、β、Ma分别为飞行器的飞行攻角、侧滑角和飞行马赫数，dX、dY、dZ分别为滚转、航向和俯仰舵偏角，XLLP、YLLP、ZLLP、MXLP、MYLP、MZLP分别为阻力系数、升力系数、侧向力系数、滚转力矩系数、偏航力矩系数及俯仰力矩系数拉偏因子，DXLP、DYLP、DZLP分别为滚转舵效、偏航舵效及俯仰舵效拉偏因子。在进行蒙特卡洛仿真时，各气动力系数的拉偏因子均设置为独立分布的随机变量，并符合均值为0、标准差为0.067的正态分布 （即拉偏量为±20%）。

2.2 仿真结果分析

在飞行器的飞行包络范围内，选取了三种典型弹道 （分别对应近程、中程和远程弹道），进行了蒙特卡洛仿真，并对脱靶量进行统计。图2为不同的惯导状态切换时间下，平均脱靶量的仿真统计结果，其中，tsw为状态切换时刻，tend为弹道总的飞行时间。

由图2可知，若组合导航系统状态切换时刻较早，由于剩余飞行时间较长，飞行器控制系统有足够的时间纠偏，弹道飞行正常，脱靶量较小;若切换时刻靠后，容许消除纯惯性导航误差的时间缩短，且切换时刻越接近弹道末段，其影响越大，甚至导致弹道异常或发散，最终表现为较大的脱靶量。图3为弹道异常下的飞行器俯仰角变化曲线。

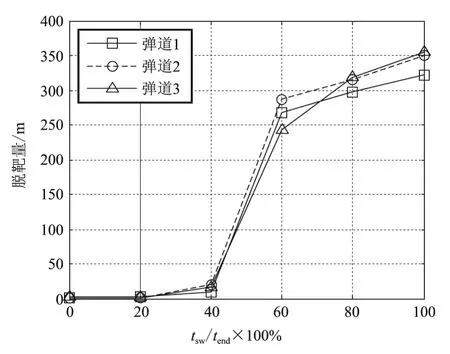
图2 不同状态切换时间下的平均脱靶量Fig.2 The curve of average miss distance with different switch times

图3 异常弹道下的俯仰角曲线Fig.3 The curve of pitch angle（abnormally trajectory）

2.3 影响分析

通过分析仿真中出现的非正常弹道，组合导航系统状态切换的影响主要体现在以下两方面:

1）纯惯性导航误差导致指令发出延后。当组合导航系统状态切换时，若纯惯性导航的水平位置误差为负，由于导航误差的影响，导弹认为的弹目相对距离较真实弹目的相对距离大。这时切入组合导航状态，纯惯性导航误差被消除，弹目相对距离骤减，迫使导弹剧烈俯冲，因剩余飞行时间较短，导弹飞过目标，弹道发散，如图3（a）所示。

2）纯惯性导航误差导致指令发出提前。当组合导航系统状态切换时，若纯惯性导航的水平位置误差为正，由于导航误差的影响，导弹认为的弹目相对位置比真实弹目的相对位置小，导弹提前按大落角俯冲。这时切入组合导航状态，纯惯性导航误差被消除，弹目相对距离骤增，由于落角的限制，导弹被迫抬头飞行，而后再低头俯冲，弹体姿态变化剧烈，速度大幅下降，末段可用过载降低，脱靶量大，如图3（b）所示。

3 改进方案设计

由第2节分析可知，若惯导状态切换时刻在飞行弹道的末段，制导控制系统一方面需实现预定落角，一方面还需控制导弹进行机动以纠偏误差，使得过载需求骤增，而实际过载能力不能满足需求，导致弹道飞行异常。在这种情况下追求大落角并不可取，可从降低落角约束导引律带来的过载需求、增大导弹纠偏机动的可用过载两方面进行改进方案设计。

3.1 方案1

带落角约束导引律的设计目标是使得目标高低角达到预定落角，并使导弹的弹道倾角逐步接近目标高低角，进而达到预定落角。式 （7）为一种广泛使用的带落角约束的导引律形式。

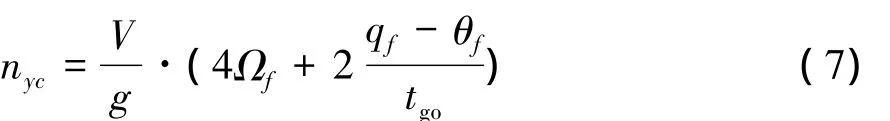
其中nyc为法向过载指令，V为飞行速度，qf为目标高低角，Ωf为弹目视线角速度，tgo为剩余飞行时间，θf为弹道的期望落角，g为重力加速度。

可见导引律由两项组成，即纯比例导引项和落角约束项，纯比例导引项保证脱靶量在一定范围内，而落角约束项使得末段落角满足需求。经上述分析，为降低导引律带来的机动过载需求，可在组合导航系统进行状态切换时，将弹道的预定落角θf设定为状态切换后的目标高低角qf，由式 （7）可知，该方案可大大降低落角约束项带来的过载需求，使得纯比例导引项的可用过载增加，提高命中精度。

3.2 方案2

方案1虽然简单，易于实施，但若实际飞行中的纯惯性导航误差并不大，惯导状态切换前后的目标高低角变化很小时，采用方案1将预定落角设置为当前的目标高低角值，会影响最终的弹道落角，方案1的设计较为保守。

为降低惯导切换输出跳变对落角的影响，需推导预定落角的设定与切换前后目标高低角的变化值之间的关系。首先，分析标准弹道条件下，目标高低角和弹道倾角 （θ）的响应曲线，如图4所示。

图4 标准弹道下目标高低角和弹道倾角变化曲线Fig.4 The curve of qfand obliquity of trajectory（standard trajectory）

由图4可知，落角约束的导引律使得目标高低角和弹道倾角逐渐向预定落角接近，在弹道末段达到预定落角，故可以认为当前时刻与弹道末端时刻制导控制系统允许的目标高低角变化幅值即为预定落角和当前时刻的目标高低角之差。

图5为组合导航系统存在状态切换时的目标高低角解算曲线，其中qf_pre为惯导状态切换前一周期的qf解算值，qf_new为惯导状态切换后一周期的qf解算值，故切换时刻前后的目标高低角的跳变幅度为Δqf=qf_new－qf_pre。由上面的分析可知，切换时刻至弹道末端控制系统允许的目标高低角的变化量为

图5 惯导存在状态切换时的目标高低角变化曲线

Fig.5 The curve of qf（with the state switch of INS）

其中，θcx_pre为惯导状态切换前的预定落角。惯导状态切换后，导引控制规律和飞行器气动外形没有变化，故可认为允许的目标高低角变化量仍为A，即

其中，θcx_new为惯导状态切换后的预定落角，由式 （8）及式 （9）可得

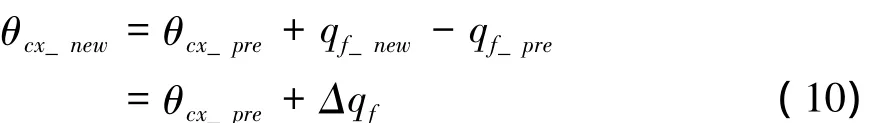
由式 （10）可知，惯导状态切换后的预定落角由状态切换前的预定落角及目标高低角的跳变幅值解算得到，即式 （10）将惯导状态切换后的预定落角设置与目标高低角的跳变幅值联系在一起，这使得预定落角可以根据惯导切换前后的纯惯性导航误差的大小进行设置，若惯导状态切换时的纯惯性导航误差较小，Δqf也较小，式 （10）解算出的预定落角变化不大，不会影响弹道落角;而若惯导状态切换时的纯惯性导航误差较大，使得Δqf较大时，式 （10）也能很好地根据目标高低角的跳变幅值和符号对预定落角进行重新设定，降低落角导引律对弹体过载的需求，增大导弹对导航误差的纠偏能力，从而实现了对纯惯性导航误差的自适应。下面进行仿真分析。

4 蒙特卡洛仿真分析

本节以弹道1为例，采用第3节分析的方案进行蒙特卡洛仿真，统计得到不同方案下的平均脱靶量及落角随惯导状态切换时间的对比曲线，如图6及图7所示。

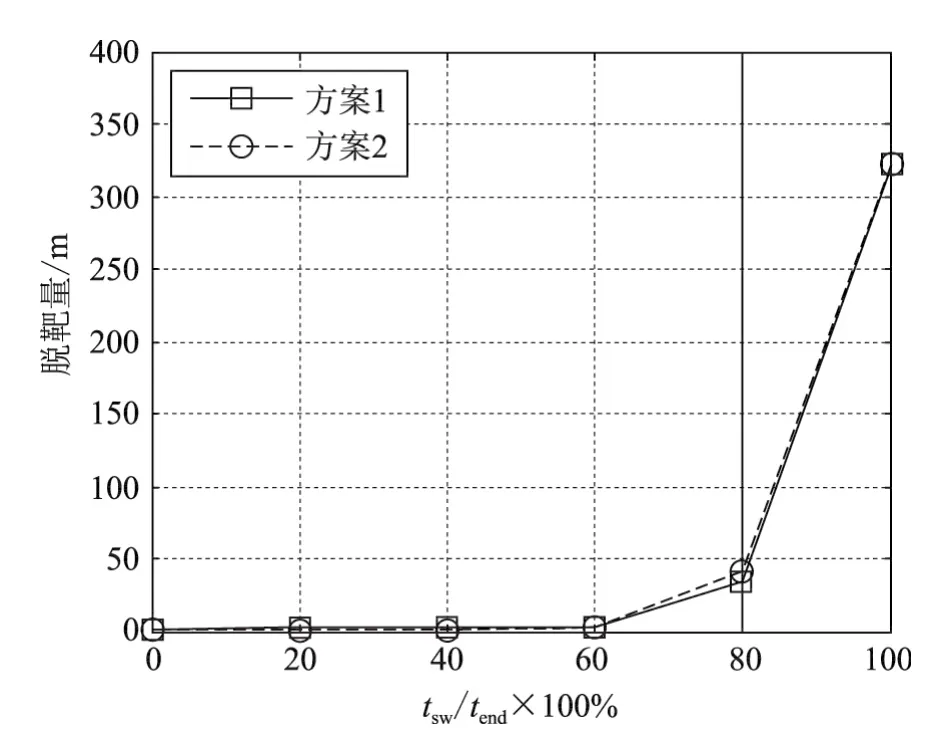
图6 不同方案下的平均脱靶量对比Fig.6 The curve of average miss distance with different solutions

图7 不同方案下的平均落角对比Fig.7 The curve of average impact angle with different solutions

可以看到，采用改进后的方案，提高了惯导状态切换条件下的命中精度，仅当惯导状态切换时刻位于弹道末段时才会产生较大脱靶量，而这主要受导弹过载能力的限制。

由蒙特卡洛仿真结果还可看出，两种方法的命中精度较为接近，但弹道落角相差较大，特别是切换时刻较为靠前时，因飞行时间较短，纯惯性导航误差较小，方案2下的弹道落角基本位于50°的预定落角附近，对落角影响较小，而方案1对落角的影响较大。

5 结论

本文分析研究了组合导航系统状态切换对末段导引的影响，并进行了改进方案的设计和对比研究。通过蒙特卡洛仿真结果可知，自适应更改预定落角方案可提高惯导状态切换条件下的命中精度，并降低了对弹道落角的影响。

本文提出的分析方法及优化方案完成了蒙特卡洛数学仿真验证，后续需针对该方案，进行制导控制系统半实物仿真试验，以对研究的合理性和有效性进行更为全面的验证。

［1］曾德贤，赵继广．组合导航系统在导航战中的作用［J］．中国测绘，2005，1:44-45．

［2］朱国栋，雷虎民．巡航导弹的GPS/INS组合导航系统研究［J］．探测与控制学报，2007，29:31-34．

［3］李小龙，段凤阳．GPS失效时组合导航系统修正方法研究［J］．计算机测量与控制，2011，7:1668-1693．

［4］钟丽娜，刘建业，李荣冰，王融．载波平滑伪距紧组合导航系统鲁棒自适应滤波算法［J］．中国惯性技术学报，2014，22（2）:205-210．

［5］周卫东，蔡佳楠，孙龙．GPS/SINS超紧组合导航系统自适应混合滤波算法［J］．哈尔滨工业大学学报，2014，46（7）:47-52．

［6］林雪原．无反馈多级式多传感器组合导航系统［J］．中国空间科学技术，2012，2:21-26．

［7］陈帅，雷浩然，薄煜明，徐芹丽．航空时敏炸弹SINS/GNSS组合导航系统设计［J］．中国惯性技术学报，2014，22（2）:21-26．

［8］程建华，李明月．基于小波分析的容错组合导航系统故障检测算法研究［J］．宇航学报，2012，33（4）:419-425．

［9］李常平，胡恒章，张志高．采用捷联惯导系统的反辐射导弹抗关机制导方案研究［J］．中国惯性技术学报，1998，（2）:19-23．

［10］周荻．寻的导弹新型导引规律［M］．北京:国防工业出版社，2002:5-8．

［11］陈海东，余梦伦，董利强．具有终端角度约束的机动再入飞行器的最优制导律［J］．航天控制，2002，（1）:6-11．