伪卫星共视法时间同步模型及其精度分析
李东新,杨伟才,常 青,李 晶,于 渊
(1.北京航空航天大学电子信息工程学院,北京 100191;2.交通信息通信技术研究发展中心,北京 100011)
0 引言
精确测量接收信号与发射信号之间的时间差(简称时差)是卫星导航定位系统测距的基础,而高精度时差测量的前提是各个观测量之间时间同步。因此,高精度时间基准的建立、维持和同步技术是建立导航定位系统的重要技术之一,也是评价导航系统的一个重要指标,同样,对于伪卫星系统,时间同步技术也尤为重要。高精度的时间同步不仅体现在从测距精度上影响用户的导航定位,还体现在通过卫星星历影响用户的导航定位[1]。因此,伪卫星系统必须有较高精度的时间基准,伪卫星之间必须保持严格的时间同步。
在高精度时间同步方法上,最先开始的是GNSS单向时间传递,但这种方法受到电离层、对流层等环境因素影响较大,从而导致同步授时精度较差。1980年美国国家标准局提出共视时间传递的方法[2-3],1983年该方法用于国际守时实验室的原子钟之间的时间比对,这时采用的大多是单通道GPS C/A码共视接收机。
共视法具有成本低、性能稳定可靠等多种优势,BIPM(国际计量局)每半年发布一次共视时刻表,参与共视比对的站点根据共视时刻表上的时刻,同时接收同一颗卫星的信号,事后通过通信网数据交换实现两站原子钟之间的时间同步。
伪卫星系统是由分布在不同地点,播发导航信号的发射器组成,这些发射器大多分布在地面或者近地空中,用以增强卫星导航系统定位测速的性能,也能够单独实现导航定位。时间同步技术是伪卫星系统重要技术之一,本文首先简述伪卫星共视法时间同步原理,在此基础上,对影响共视法时间同步模型精度的各种误差进行深入分析。
1 伪卫星共视法时间同步原理
伪卫星共视时间同步,指的是需要完成时间同步校准的伪卫星,仅单方向同时接收同一颗导航卫星发出的时间信息,并利用该时间信息完成本地时钟同步校准的一种方法。具体做法是,在一颗GNSS卫星的视角内,地球上任意两个地点的伪卫星的原子钟利用同一时间收到的同一颗卫星的时间信号进行时间频率比对。共视时间同步方法通过消除两个伪卫星对同一颗卫星观测的信号传播路径上的共有误差来实现高精度的时间同步,其原理如图1所示。

图1 GNSS共视时间同步原理图Fig.1 Principle of GNSS Common-view time synchronization
若A、B两个伪卫星上放置的接收机在同一时刻观测到同一颗卫星i的伪距为ρiA和ρiB,通过对伪距观测量进行各项误差和延迟的修正,得到A、B两个伪卫星观测站的接收机钟差分别为 δtA和δtB:

riA,riB表示卫星i与伪卫星A、B之间的真实几何距离;(xi,yi,zi)表示卫星i的三维位置坐标;(xA,yA,zA),(xB,yB,zB)分别表示伪卫星A、B的三维位置坐标;δti表示卫星i的钟差;IiA、IiB分别表示卫星i与伪卫星A、B之间的电离层延时,TiA、TiB分别表示对流层延时;εiA、εiB表示未直接体现在公式中的各种误差的总和。事后,两观测站通过通信交换监测数据,对式 (1)、式(2)两式作差

其中,ΔIiAB=IiA- IiB,ΔTiAB=TiA- TiB,ΔεiAB=εiA-εiB,等号左边第一项(δtA-δtB)为伪卫星A与B之间钟差,在计算出伪卫星A与B两地钟差之后,我们就可以对伪卫星A、B上的时钟进行间接比较,共视法时间同步原理与差分GNSS类似,当两个需要同步的伪卫星之间相距较近时,他们两者之间的测量误差基本可以全部被抵消掉,共视法就能取得很好的时间同步效果。
2 共视法时间同步误差分析
由式 (3)可以看出,共视法可以完全抵消星钟误差[4],抵消大部分的星历误差,当A、B两站相距1000km以内时,共视法可以抵消单向时间同步中95%以上的星历误差,此外,共视法还可以部分抵消电离层延迟和对流层延迟误差[5-6]。抵消后的电离层残差ΔIiAB,对流层残差ΔTiAB,以及由于多径效应、接收机噪声等引起的残差ΔεiAB,对伪卫星共视法时间同步授时精度具有决定性作用,设电离层延时残差的1σ误差为δI,对流层延时残差的1σ误差为δT,其他残差项的1σ误差为

下面对这些残差项分别分析。
2.1 电离层延时残差
电离层是指从地面70 km以上直到大气层顶端(约1000km)的大气层。由于太阳的作用,使大气的分子发生电离,当电磁波穿过充满电子的电离层时,传播速度和方向就会发生改变,传播速度的改变量就造成了电离层延时。由于伪卫星之间相距几十甚至几百公里,从而导致电磁波传播的路径不完全相同,电离层延时就不能完全抵消,从而就产生了电离层延时残差,这种残差不仅与两颗伪卫星之间距离有关,而且还与伪卫星在地球纬线 (南北方向),还是经线方向 (东西方向)相距有关。
在单频接收机中,可以通过电离层网格模型内插和外推来获取较准确的电离层延时改正值,本文分析电离层延迟残差就是利用这个方法,IGS网站提供的全球电离层图是电离层网格模型的数据基础,用户通过在电离层格网中内插计算电离层穿刺点处垂直电子含量 (VTEC),然后根据VTEC值计算穿刺点垂直方向电离层延迟,最后将其投影到电磁波传播路径上,从而得到最终的电离层延迟。通过网格模型计算电离层延迟的步骤如图2所示。
根据图2所示,首先计算穿刺点经纬度。根据接收机、穿刺点和卫星之间的关系,设φM、λM分别是穿刺点的椭球纬度和经度,则有:δε,可知共视法时间同步的精度δ可表示为

其中,φu是用户地理纬度,λu为用户地理经度,A为卫星方位角,ψ为用户和穿刺点的地心张角。由于IGS电离层网格数据文件是按照地心纬度划分的,因此需要对式 (5)中大地经度和纬度进行经纬变换,设穿刺点的地心经度、纬度分别为λ*M、φ*M,公式如下:


图2 网格模型计算电离层延迟流程图Fig.2 The flow chart of calculating ionosphere delay by the grid model
其中,fWGS84=1/198.257224表示WGS84椭球扁率。
有了穿刺点地心经度、纬度,通过电离层格网文件插值法就可以计算出穿刺点垂直方向电子含量,插值方法采用与信号接收时刻最近的两个TEC区域,表达式如下
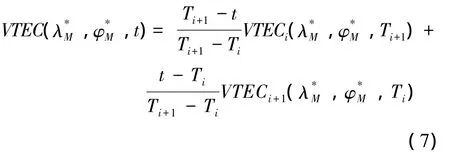
对于TEC区域内,建立全球性VTEC模型可以采用球谐函数模型[7],建立区域性的可以采用曲面拟合模型、距离加权模型以及多面函数模型,具体插值方法可查阅相关插值文献。本文采用距离加权模型进行插值计算。
求出垂直方向电子浓度之后,设为Nz,需要对其进行投影,投影到电磁波传播方向上,公式如下[8]:

其中,Iz表示垂直方向电离层延时,f表示电磁波频率,F为倾斜率,θ是以弧度为单位的高度角,这样就求出了电离层延时I。
通过对同一时刻两颗伪卫星对同一颗卫星观测电离层延时作差就得到电离层延时残差,我们通过网格模型来分析共视法时间同步中电离层延时残差,通过分析伪卫星间距方向、不同伪卫星间距、共视卫星高度角等三方面。
2.2 对流层延时残差
由于对流层延迟是非弥散延迟,对L1和L2频率延迟相等。通过研究,人们发现对流层延迟可以分为干延迟和湿延迟两部分,前者较为稳定,占90%,后者与水气含量及分布有关,占10%,且各延迟量与卫星高度角成明显的函数关系。但传播路径上的折射率及气象参数很难得到,于是根据一些代表性的气象资料,用解析的方法,以地表面的气象参数近似反映天顶方向上的气象时空变化,产生中性大气天顶延迟的模型。近似方法不同而模型也各异。这种估计天顶延迟的方法通常也称为模型改正法[9]。
具有代表性的模型是 Saastamoinen模型[10]和Hopfield模型[11]。Saastamoinen模型需已知大气折射廓线及干、湿对流层和干平流层各层的边界值,采用中纬度地区的美国大气模式来确定系数,再列表插值;Hopfield模型是根据对全球高空气象探测资料分析,采用的经验系数是用全球18个台站1年的平均资料得到的。Saastamoinen将温度梯度作为常数分两层计算,而Hopfield按单层计算,比较简单。两种模型在高度角较大时,精度没有明显区别。其中Hopfield模型由于涉及参数最少,实现较为容易。
本文采用Hopfield模型算法,卫星信号传播路径上对流层延迟改正如下[11]。


其中,Nw表示湿分量折射数,Tk0表示在地面上高度为0处的热力学温度。
由于伪卫星站之间位置的差异导致对同一颗共视卫星观测时高度角有所不同,从而导致利用共视法消除对流层延迟产生残差,而这个残差是共视法时间同步授时的一个重要组成部分,通过Hopfield对流层延迟误差模型,我们可以对对流层残差进行分析。
2.3 多径效应、接收机噪声、星历等其他残差
多径效应是由环境因素导致卫星信号经过多次反射后进入共视接收机,由于伪卫星固定在地面不动,不同伪卫星所处的环境也不同,导致产生的多径效应不能抵消,对于静态接收机,多径效应产生的误差值也不呈现正态分布,而是随着卫星的移动呈周期性正弦波动。由于多径效应一般引起 1~5m的伪距误差[8],这部分误差很难消除。
接收机噪声包括天线、放大器和各部分电子器件热噪声等引起的误差,这部分误差具有随机性,其正负很难确定,一般来说,接收机噪声误差在 1m 左右[8]。
星历误差是由于星历中给出卫星真实位置不
式(9)~式(12)中,E为卫星相对用户接收机天线的仰角,p为标准大气压,Tk为273.16K,hu为用户的高度,ηd、ηw分别为对流层干分量和湿分量修正系数,hd是以海平面为基准的对流层干分量的上限,hw是对流层湿分量的上限hw=11000,也可由式 (13)确定准而引入的误差,星历误差一般在1m左右[12]。
3 仿真分析
3.1 电离层延时残差仿真分析
电离层延时残差可以用网格模型来计算。本次用GPS导航卫星作为共视卫星来仿真分析,首先用GPS导航接收机接收卫星导航信号,解算卫星导航电文并存储,同时从IGS网站上下载全球电离层格网数据文件,利用以上两种文件,通过网格模型计算出同一时刻需要同步的两颗伪卫星之间电离层延时,然后作差分析。
利用网格模型,设定伪卫星A位于地球表面,纬度和经度为39.9790°N,116.3448°E,伪卫星 B距离A为500km时,分别在经线 (东西)和纬线(南北)方向上1个月时间内电离层残差的曲线如图3及图4所示。

图3 纬线方向电离层延时残差曲线Fig.3 The curve of ionosphere delay residuals in the direction of latitude

图4 经线方向电离层延时残差曲线Fig.4 The curve of ionosphere delay residuals in the direction of longitude
由图3和图4可以看出,共视法电离层延时残差具有一定的周期性,大约是以天为周期,在经线 (东西)方向相距比在纬线 (南北)方向相距残差波动更大,统计可知,在纬线方向残差误差为0.7388ns,而在经线方向残差误差为1.0171ns。
下面,我们来分析两颗共视伪卫星观测站间距对电离层延时残差的影响。电离层残差与电磁波穿过电离层路径有关,两颗伪卫星观测站相距越远,电离层路径差异越大,从而带来延时残差越大,电离层延时残差与距离相关仿真曲线如图5所示。

图5 电离层延时残差随距离变化曲线Fig.5 The curve of the ionosphere delay residuals with different distances
由图5可以看出,无论经线还是纬线方向,距离越远,共视法电离层残差越大;随着距离增加,经线方向残差增长的更快,所造成授时误差更大。很多共视法时间同步授时选择使用中继方法来减小由于距离太远而导致电离层延迟残差较大的问题,从而提高精度,同时,纬度方向中继站更有利于提高授时精度。
除此之外,卫星高度角也会对电离层延迟残差产生较大影响,卫星高度角引入的误差将直接影响倾斜率F,则倾斜率F与卫星高度角之间关系如图6所示。

图6 倾斜率F及其变化率随高度角变化曲线Fig.6 The curve of tilt rate F and its rate of change with different elevation angles
由图6可以看出,随着高度角的增大,倾斜率变化率逐渐减小,对于相同的高度角差的情况下,高度角越大,F的变化率的绝对值越小,从而对最终残差的影响也就越小。由此可见,选择高度角较大的共视卫星更有利于提高同步授时精度。
3.2 对流层残差仿真分析
对流层延迟残差可以采用Hopfield模型来计算。在模型中,影响对流层延时误差主要因素是高度角,通过GPS导航接收机接收到的导航文件可以解算出卫星位置,而通过卫星位置和接收机位置可以解算出卫星高度角,最后通过Hopfield模型计算对流层延时残差。
对流层延时误差随高度角变化的关系如图7所示。
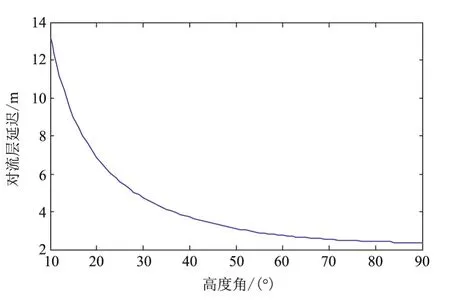
图7 对流层延时误差随高度角变化曲线Fig.7 The curve of tropospheric delay error with the change of elevation angle
从接收机星历文件中,选取卫星号为9,23,27三颗卫星作分析,伪卫星A位置为39.9790°N,116.3448°E,伪卫星B与A相距500km时,三颗卫星相对伪卫星A、B高度角和对流层延时残差的仿真曲线如图8、图9和图10所示。
由图8、图9和图10可以看出,随着高度角的增大,共视法对流层残差逐渐降低。距离、卫星位置等都是通过高度角的不同来影响对流层残差,进而来影响共视法时间同步的精度,在高度角较高 (80°~90°)时,对流层引起的残差最小可达0.1ns;在高度角较小 (30°以下)时,对流层引起的残差高达1.5ns,可见,选择高仰角卫星共视对对流层残差的减小具有重要的作用。

图8 9号星相对于伪卫星A、B的高度角变化和延时残差仿真曲线Fig.8 The simulation curve of elevation angle between No.9 satellite and the pseudolite A and B and the residual delay
3.3 精度分析
根据以上分析,当选择纬线方向和较大高度角的共视卫星时,可以提高精度。当A、B伪卫星基站相距从50km~1000km变化时,由于星历误差导致误差为 1m[12],共视法1000km内可以消除95%误差,消除后残差为0.05m,接收机热噪声取1m,多径效应取1m[12],倾斜率F取2,从而得到时间同步精度随距离变化的曲线如图11所示。

图9 23号星相对于伪卫星A、B的高度角变化和延时残差仿真曲线Fig.9 The simulation curve of elevation angle between No.23 satellite and the pseudolite A and B and the residual delay
由图11可以看出,在两个伪卫星站相距较近时,经线纬线方向同步精度相当,随着站间距的增加,经线方向误差急剧增加,授时精度急剧下降,而纬线方向误差仍然缓慢增加。当站间距达到1000km时,同步精度最大可以达到2ns。由此可见,纬线方向分布伪卫星站更加有利于提高共视法同步授时精度。分析可知,由于不同经线方向具有不同的太阳时,太阳辐射角具有较大差异,而在纬度方向处于同一个太阳时,太阳光对电离层辐射强度相差不大,从而导致电离层变化缓慢。

图10 27号星相对于伪卫星A的高度角变化和延时残差仿真曲线Fig.10 The simulation curve of elevation angle between No.27 satellite and the pseudolite A and B and the residual delay
4 结论
通过本文分析,我们可知,使用简单的单通道伪码共视接收机,我们即可保证在1000km内实现伪卫星A、B两站优于8ns的时间同步精度。选择纬度方向上分布伪卫星和较大的高度角更能够减小残差,提高精度。目前,BIPM已将共视作为全球70多个守时实验室之间时间比对的主要手段之一。
两伪卫星基站进行GNSS共视法时间同步的前提条件是两站在同一时刻共视同一颗卫星,两站相距越远,共视的卫星数目越少,两站获得的共视卫星的观测数据质量越低。通过电离层仿真分析结果可以证明,要进行时间比对的两站必须严格按照规定的共视时刻表观测。此外,还需要在两站之间建立数据传输网络,供事后数据交换使用。因此,GNSS共视时间传递不满足实时性,有延时滞后,这些都是GNSS共视存在的局限性。

图11 共视法时间同步精度随距离变化曲线Fig.11 The curve of the precision of the common-view time synchronization with different distances
[1]郭海荣.导航卫星原子钟时频特性分析理论与方法研究[D].郑州:信息工程大学,2006.
[2]Allan D W,Weiss M A.Accurate time and frequency transfer during common-view of a GPS satellite[R].Proceedings of the 1980 Frequency Control Symposium,1980:334-346.
[3]Levine J.A review of time and frequency transfer methods[J].Metrologia,2008,45(6):S162.
[4]张鑫,韩小余,应洪伟.GPS共视技术中不确定度分析[J].宇航计测技术,2008,10,28(5):31-33.
[5]王正明.GPS共视资料的处理和分析[J].天文学报,2001,42(2):184-191.
[6]孙宏伟,李岚,苏哲斌.卫星位置误差对GPS共视时间比对的影响[J].武汉大学学报 (信息科学版),2009,34(8):968-970.
[7]Haines G V.Spherical cap harmonic analysis[J].Journal of Geo-physical Research:Solid Earth(1978-2012),1985,90(B3):2583-2591.
[8]GPS原理与接收机设计[M].电子工业出版社,2009.
[9]杨开伟,甘兴利,李娟娟.三种全球对流层改正模型特性分析[C]//.第三届中国卫星导航学术年会论文集,2012,5,中国广东广州.
[10]Saastamoinen J.Contributions to the theory of atmospheric refraction[J].Bulletin Géodésique(1946-1975),1973,107(1):13-34.
[11]Hopfield H S.Two‐ quartic tropospheric refractivity profile for correcting satellite data[J].Journal of Geophysical research,1969,74(18):4487-4499.
[12]The Global Positioning System,GPS Error Sources.Available at http://www.colorado.edu/geography/gcraft/notes/gps/gps_f.html.

