不同定位精度INS下的重力匹配算法适用性研究
刘繁明,姚剑奇,荆 心,程 石
(哈尔滨工程大学自动化学院,哈尔滨 150001)
0 引言
随重力测量精度的不断提高,出现了依靠重力场特征定位的重力辅助导航方法[1-2]。该方法依靠重力测量的无源性及重力场的时空稳定性,保证导航的隐蔽性及可靠性。此外,至今已积累了大量的船舶及航空重力测量数据。综上所述,重力辅助导航是具有现实意义的,稳健的辅助导航方法。
目前对重力辅助导航的研究主要集中在匹配算法[2-6]及重力场导航适配性[7]的研究上,而重力辅助导航以惯性导航为基础,除匹配算法及重力场特征外,INS误差特性将影响匹配算法的性能。本文通过对几种经典的相关及滤波匹配算法的研究及仿真实验说明:因不同匹配算法的特点不同,INS定位精度变化会改变算法间的优劣关系,导致匹配算法的适用性变化。
1 相关匹配算法
1.1 TERCOM算法
设匹配序列长度为L,k时刻量测向量gk由k至k-L+1时刻重力量测组成。在基准图一定范围内,按固定步长移动INS航迹并插值得向量gmi,i=1,…,N(N为向量总数),则由式 (1)可得匹配位置

()为INS航迹经向、纬向平移量。TERCOM可视为INS航迹沿基准等值线滑动和垂直其滑动以寻找相关峰过程,其定位误差如图1所示。
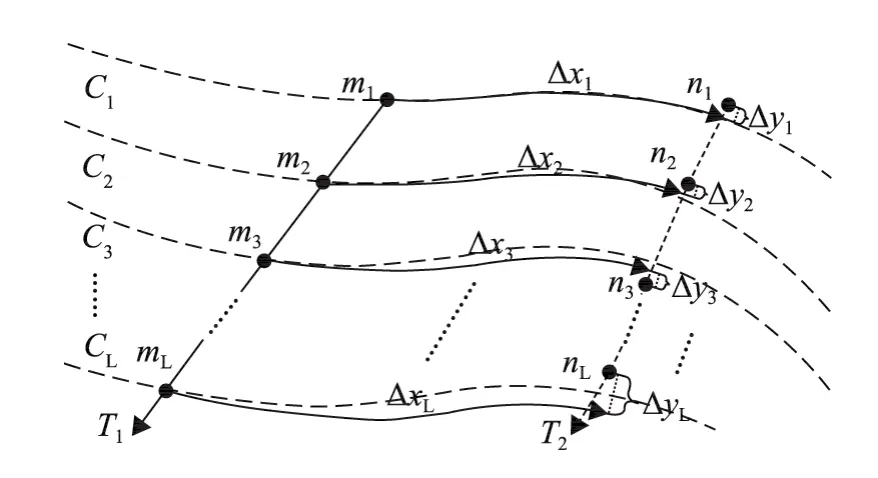
图1 TERCOM定位误差示意图Fig.1 Diagram of positioning error of TERCOM
图1中,T1、T2为真实及匹配航迹,mi、ni为量测点,i=1,…,L,Ci为mi等值线。以C1为基准,T2相对T1的偏差为:ni相对mi沿C1滑动及垂直C1滑动的偏移Δxi、Δyi。设mi对应制图误差、量测噪声及 INS速度误差所引起的 Eötvös效应[8]改正误差 (以下简称 Eötvös误差)之和为 δMi,则Δxi、Δyi如式 (2)所示:

hxi为Si沿C1滑动时,因Ci与C1不平行所致的重力变化率。hyi为Si垂直C1滑动时的重力变化率。λx和λy为两方向滑动步长,Nx、Ny为滑动步数。因INS误差积累,Δxi、Δyi随i递增,ζxi、ζyi为递增的部分,且ζx0=ζy0=0。若考虑ζxi、ζyi的影响,式 (2)须改为

1.2 ICCP算法
ICCP算法如图2所示。
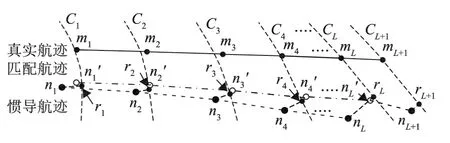
图2 ICCP定位示意图Fig.2 Diagram of positioning of ICCP
mi为真实量测点,Ci为mi等值线,ni为INS航迹量测点,ri为Ci上的ni最近点,i=1,…,L+1。n1'至n'L为匹配航迹,L为匹配序列量测点数。寻找刚体变换[2],使 { ni}Li=1与 { ri}间距离平方和最小。以下为算法步骤:
i基准图上寻找ni最近等值线点ri,i=1,…,L。
2)计算刚性变换,使ni移至n'i并代替原ni。
3)循环步骤1)、2)至刚性变换很小或循环次数超过阈值,得匹配序列ni,i=1,…,L。
待 { ni}匹配完毕,由 nL+1与 ni,i=2,…,L组成新序列,按以上步骤得nL+1匹配位置,以此类推。

ICCP的旋转操作可降低INS航迹形变对定位的影响。但当INS精度提高时,航迹形变减小,等值线分布、量测噪声、Eötvös误差对ri定位的影响所导致的航迹旋转角误差,反而使旋转操作成为ICCP的劣势。
王虎彪等人提出了最小均方误差旋转拟合算法[6],以下简称MMSE旋转拟合算法,其逐步旋转参考航迹并仿照TERCOM做平移及相关运算以寻找相关峰。此外,算法以最优匹配航迹始端8邻域网格点为起始点寻找8条次优航迹,与最优航迹按相关值加权得最终匹配航迹。该算法可降低INS航迹形变对匹配的影响且不依赖局部等值线分布。但对于高精度INS,其航迹旋转操作同样可能影响匹配精度,且计算量较大。
作为匹配算法的基准,INS精度的提高必然有利于匹配定位精度的提高,但由以上研究可知,其对不同算法的有利程度不同:完全有利于TERCOM,而对ICCP及MMSE旋转拟合算法则兼有利弊。此外,相关匹配完全由量测信息定位,当INS精度提高时,量测噪声将成为影响匹配精度的重要原因。
2 滤波匹配算法
滤波匹配可分为大误差的并行Kalman滤波匹配[5]和小误差的局部线性化 Kalman滤波匹配算法[4]。
2.1 并行Kalman滤波匹配算法
(1)算法原理
以INS位置为中心确定搜索区域并设置规则分布的Kalman滤波器,如图3所示。
该算法假设距载体最近的滤波器filter(*)满

图3 并行滤波器配置Fig.3 The configuration of parallel filter
足式 (4)的系统及量测方程,X(*)k、Z(*)k为状态量与量测量。

SWRSmin为SWRS最小值,SWRSmin*为SWRSmin滤波器邻域Ω以外的SWRS最小值。Thre为阈值,这里N为SWRSmin邻域Ω内滤波器连续为SWRSmin次数。最终由式 (7)得匹配位置(x*,y*):
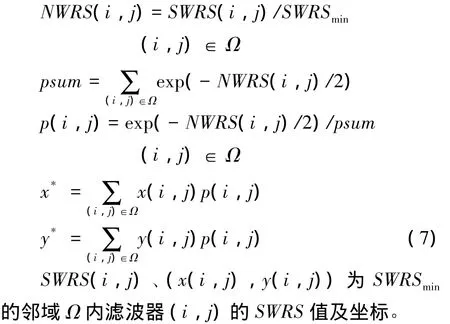
2.2 局部线性化Kalman滤波匹配算法
(1)算法模型
该算法系统方程如式 (8)。状态为经度、纬度位置误差及东、北向速度误差估计:X=[δλk,δφk,δvEk,δvNk]T。

N为滤波周期,Fk为只考虑位置与速度信息的INS误差方程,具体形式见文献 [9]。Zk如式 (9)所示

(2)定位误差研究及定位精度提升方案
重力场局部区域对应的观测阵Hk缓变,以下直观描述定位受Hk缓变的影响:由位置误差及量测量物理意义可将滤波状态更新,可表示为式(10),dk如图4所示,Kk为滤波增益。




图4 位置估计更新示意图Fig.4 Schematic diagram of the position estimate update
等值线Ck缓变对定位的影响无法避免,但可减弱与滤波增益相关的θk对匹配的影响。对于定位而言,相对重力场局部变化幅度,目前的重力测量尚未达到很高的精度;由文献 [10]的分析可知,Hk缓变降低了系统的可观测性,使残差中带有Eötvös误差;由图4知,仅增大 θk幅值不能使其沿Ck分量指向真实位置O。以上因素使得根据残差调节滤波增益的方法往往产生较大的匹配误差,这与文献 [11]的实验结果近似。为便于分析,仅考虑位置误差系统:因无先验信息,取初始方差为等元素对角阵,即P0=diag(σ2,σ2)。短时间载体航行距离短,其近似处于直角坐标系,Φk,k-1为单位阵,Hk近似常值[hE,hN],则有式(11)成立

可见Xk垂向等值线移动,移动幅度逐步递减。通常设置小速度误差方差以免位置误差大幅震荡,则速度误差估计对Xk影响较小,式(12)受其影响较小。由以上分析可知,可定期重置方差阵为元素大小适宜的对角阵,以恢复滤波增益作用。此方法虽不能使Xk向真实位置O移动,但可确保减小误差且不至误匹配。
实际中,因对惯性器件常值误差估计能力较弱,式(8)的系统方程存在模型误差。此外,即使采用上述定位精度提升方案,协方差分析过程使Xk采用逐步递减的方式接近等值线,当INS误差增速较快时,其校正误差的能力反而减弱;当INS精度较高时,系统模型误差降低,Xk偏离等值线的速度降低,此时协方差分析的抗噪声能力成为滤波匹配算法的优势。
3 仿真实验
以下验证不同精度INS下的匹配算法定位情况。因较难获取实测重力数据及多种精度的INS数据,以TOPEX卫星的某海域重力数据及仿真INS数据进行匹配实验。采用的重力基准图如图5(分辨率1'×1')所示。

图5 Topex卫星重力异常数据Fig.5 Gravity anomaly data of TOPEX
设陀螺、加速度计常值误差由 εc、Ac表示,则仿真采用3种INS,INS1:εc=0.01(°)/h、Ac=10-5g;INS2:εc=0.005(°)/h、Ac=5 × 10-6g;INS3:εc=0.001(°)/h、Ac=10-6g, 陀螺及加速度计随机误差标准差为0.5倍常值误差。载体航速8节,航向北偏东50°。为验证大误差匹配能力,使3种INS具有接近的大初始误差:设INS1~3进入导航区域前,分别航行5小时、13.33小时及75小时,积累位置误差5.86'、6.13'及5.98',且3种INS的真实航迹非常接近。匹配实验时间35小时。INS航迹、真实航迹及INS航迹的经度、纬度误差如图6、图7所示。

图6 各INS航迹及真实航迹Fig.6 The tracks of INS1 to INS3 and real track

图7 INS1~3的位置误差Fig.7 The positioning error of INS1 to INS3
实验中设重力量测噪声为0均值,标准差为1mGal的白噪声。以TERCOM、ICCP、MMSE旋转拟合、并行Kalman滤波、组合滤波匹配进行实验。实验中各算法设置如下。
相关匹配的重力量测周期为6min,匹配序列含20个量测点。TERCOM航迹搜索半径为10',经度、纬度方向搜索步长为0.1'。ICCP采用先TERCOM而后转入ICCP的组合方式,其迭代次数阈值为20次,最近点搜索半径为7'。MMSE旋转拟合算法航迹旋转角范围为-8°~8°,旋转角增量步长为15',航迹搜索设置同TERCOM。
并行Kalman滤波算法滤波周期为10min,滤波器间隔为0.5',搜索半径含40个滤波器,Thre=1.7,α=0.17,INS1~3的Ω分别为以SWRSmin为中心的7×7、5×5、3×3滤波器阵列。因局部线性化Kalman滤波适用小位置误差,将其与并行Kalman滤波组合,构成搜索 (并行Kalman)与跟踪 (局部线性化Kalman)模式,简称组合滤波匹配模式。其先进入搜索模式,待有定位输出后转入跟踪模式,若残差连续5个周期超过阈值则返回搜索模式,以此循环往复。INS1~3的残差阈值为10mGal、7mGal、5mGal。跟踪模式滤波周期为1min,方差重置周期为2.5h。
每种算法各进行20次实验以统计 RMSE。INS1~3的RMSE如图8~图10,RMSE统计数据见表1~表3(滤波匹配从有稳定的定位输出开始计算统计值;表中增加总误差以比较各算法优劣:总误差=[经度误差2+纬度误差2])。

图8 INS1各算法RMSEFig.8 RMSE of each matching algorithm for INS1

图9 INS2各算法RMSEFig.9 RMSE of each matching algorithm for INS2

图10 INS3各算法RMSEFig.10 RMSE of each matching algorithm of INS3

表1 INS1各算法RMSE统计数据Tab.1 Statistical data of RMSE with different matching algorithms for INS1 (')
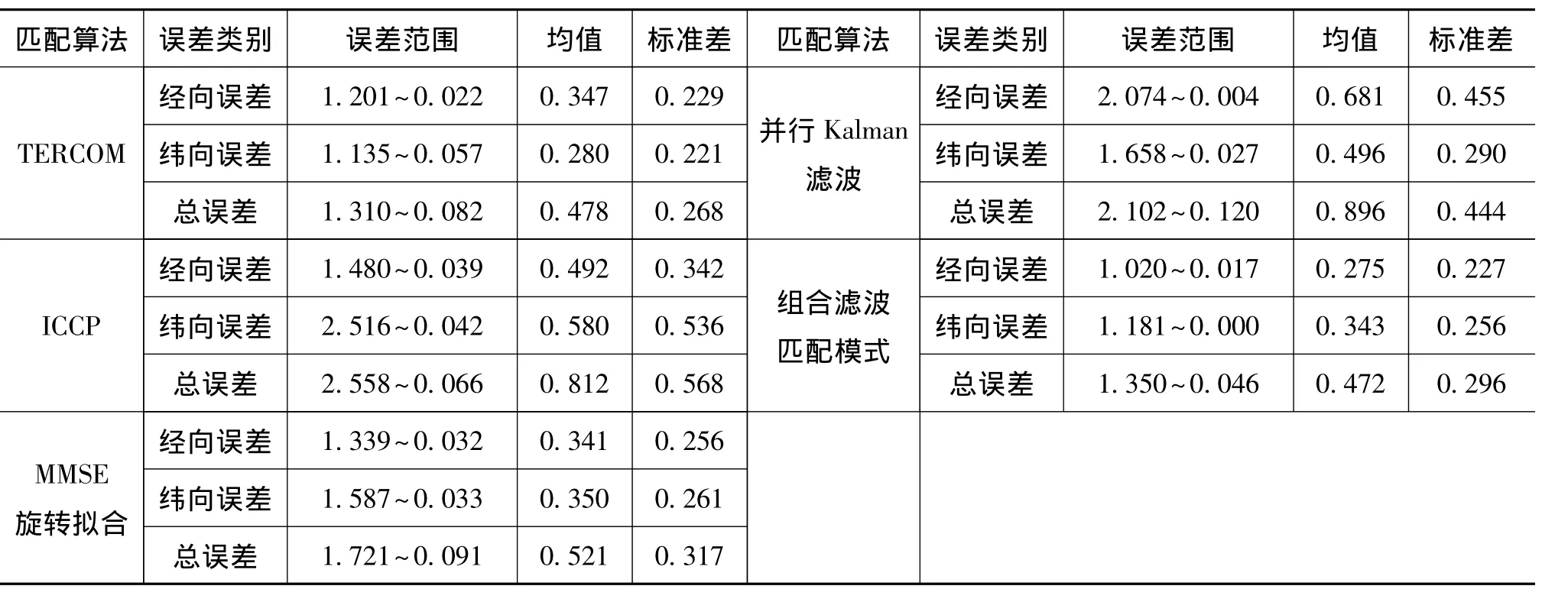
表2 INS2各算法RMSE统计数据Tab.2 Statistical data of RMSE with different matching algorithms for INS2 (')

表3 INS3各算法RMSE统计数据Tab.3 Statistical data of RMSE with different matching algorithms for INS3 (')
仿真条件:CPU P43.2GHz,1GB内存,Matlab2007仿真环境。各算法单航程平均运行时间为,TERCOM:45.6s,ICCP:660.9s,MMSE 旋转拟合:1148.0s,组合滤波匹配:18.9s。可见组合滤波及TERCOM计算量较小,而MMSE旋转拟合算法的计算量较大。
由实验数据可知,对于滤波匹配,组合滤波匹配优于单纯的并行Kalman滤波匹配;对于相关匹配,随INS精度提高,各算法的表现为,INS1:MMSE旋转拟合及ICCP的适用性较好且MMSE略优,TERCOM最差 (存在大误差情况),以最优算法总误差均值为基准,TERCOM与MMSE旋转拟合算法的精度相差59.6%;INS2:TERCOM及MMSE旋转拟合算法适用性较好且TERCOM略优,以最优算法总误差均值为基准,二者精度相差9%;INS3:TERCOM最优,其与MMSE旋转拟合的精度相差 28.6%。可见随 INS精度提升,TERCOM相对MMSE旋转拟合算法更加适用。而INS精度提高时,等值点分布对计算ICCP航迹旋转角的影响较大,其稳定性稍差。
INS1的MMSE旋转拟合精度略优于组合滤波匹配,二者精度相差7.4%;INS2的组合滤波匹配与TERCOM精度差距微弱,相差1.3%;INS3的组合滤波匹配优于 TERCOM,二者精度相差10.1%。
以上数据中,相关匹配与滤波匹配的精度差距并不明显,但当量测噪声标准差增至2mGal、3mGal时,INS3的滤波匹配基本不受影响,TERCOM误差明显增大,表明了滤波匹配在高精度INS下的适用性。而对于INS1,增大量测噪声时,各算法误差均增大且MMSE旋转拟合仍最为适用,原因为:增大量测噪声使滤波匹配的Xk(如图4)趋向等值线的步长减小,减弱抑制INS误差的能力,而INS1的误差快速增长,所以滤波匹配算法误差亦增大。因篇幅原因,此处仅说明增大量测噪声后的匹配结果,而省略实验数据。
4 结论
本文指出,因不同匹配算法的特点不同,INS精度的变化导致匹配算法的适用性变化,并得出结论:相关匹配抑制INS误差对定位影响的能力较强,但不具有抗量测噪声能力;滤波匹配可处理量测噪声,但其抑制INS误差的能力相对较弱。因此对于中等精度INS(误差增速≈1n mile/h),相关匹配的MMSE旋转拟合算法适用性较好;对于高精度INS(误差增速≈1n mile/d),滤波匹配的适用性较好。本文所得结论为搭载不同精度INS载体的重力场匹配算法选择提供依据,具有一定现实意义。
[1]Lowreys J A.Passive navigation using inertial navigation sensors and maps[J].Naval Eng J,1997,5:245-251.
[2]BEHZAD K P,BEHROOZ K P.Vehicle localization on gravity maps[C]//.Proceedings of SPIE-The International Society for Optical Engineering,1999,3693:182-191.
[3]闫利,崔晨风,吴华玲.基于TERCOM算法的重力匹配[J].武汉大学学报 (信息科学版),2009,34(3):261-264.
[4]秦政,边信黔,施小成,等.水下运载体重力辅助惯性导航系统仿真平台[J].武汉大学学报 (信息科学版),2008,33(7):755-758.
[5]戴全发,许大欣,蔡小波,等.重力异常匹配辅助导航解算模型的优化[J].大地测量与地球动力学,2007,27(4):31-34.
[6]王虎彪,王勇,方剑,等.“最小均方误差旋转拟合法”重力辅助导航仿真研究[J].中国科学:地球科学,2012,42(7):1055-1062.
[7]Yan Li,Wu Hua-ling.Research on the selection of suitable matching area in the gravity aided navigation[C]//.Proceedings of the SPIE:the International Society for Optical Engineering,2007,6752,67523U.
[8]黄谟涛,翟国军,管铮,等.海洋重力场测定及其应用[M].北京:测绘出版社,2005.
[9]黄德明,程禄.惯性导航系统[M].北京:国防工业出版社,1986.
[10]Chen Zhe.Local observability and its application to multiple measurement estimation[J].IEEE Transactions on Industrial E-lectronics,1991,38(6):491-496.
[11]王伟,李珊珊.重力异常卡尔曼滤波匹配算法的改进[A].第四届中国卫星导航学术年会论文集[C]//.2013.

