集装箱码头泊位计划的鲁棒优化模型

曾庆成, 赵孝峰, 胡祥培, 杨忠振

(1.大连海事大学 交通运输管理学院，辽宁 大连 116026; 2.大连理工大学 系统工程研究所，辽宁 大连 116023 )



集装箱码头泊位计划的鲁棒优化模型

曾庆成1, 赵孝峰1, 胡祥培2, 杨忠振1

(1.大连海事大学 交通运输管理学院，辽宁 大连 116026; 2.大连理工大学 系统工程研究所，辽宁 大连 116023 )

针对集装箱码头作业中的不确定性因素，构建泊位计划的鲁棒优化模型与算法，目的是降低不确定性因素对集装箱码头作业系统的影响。首先，提出泊位计划鲁棒性度量指标，利用算例对各指标的效果进行分析。在此基础上，设计泊位计划鲁棒优化的两阶段优化算法。算法的第一阶段不考虑泊位计划的鲁棒性，以船舶总延误时间最小为目标；算法的第二阶段以所选择的鲁棒性指标最大为目标，以第一阶段获得的船舶总延误时间为约束条件，获得鲁棒调度方案。最后，研究作业资源(装卸桥数量)的变化对泊位计划鲁棒性的影响。算例分析表明，权重松弛量是有效的度量泊位计划鲁棒性的指标，两阶段算法可以有效解决泊位计划鲁棒优化问题。

物流工程；泊位计划；鲁棒优化；集装箱码头

0 引言

泊位是集装箱码头的重要作业资源，合理的泊位计划是提高码头生产效率，减少船舶延误的重要因素。但在集装箱码头作业过程中存在各种不确定性因素，如作业事故、设备故障等。这些事件的发生可能会打乱原有泊位计划，对正常作业造成巨大干扰，引起大量的额外成本。因此，如何有效地处理这些不确定性因素，减少其对码头作业系统的影响，已成为集装箱码头作业调度领域的重要问题。

本文拟在泊位计划制定阶段，通过提高泊位计划的鲁棒性，降低不确定性对集装箱码头作业系统的影响。为此，需要解决两方面的问题：一是如何选择鲁棒性度量方法与指标；二是如何在调度方案鲁棒性与作业成本之间做出平衡。本文首先在不考虑不确定性因素的情况下，建立泊位分配模型，然后，建立泊位计划鲁棒性度量方法，设计优化泊位分配方案的两阶段算法，研究泊位计划鲁棒性与作业资源投入的关系。

1 国内外研究现状

国内外学者针对泊位分配问题开展了大量的研究，代表性研究如，Nishimura等[1]、Imai[2]和Kim等[3]建立的离散型泊位分配模型，以及Imai等[4,5]和Wang等[6]建立的连续泊位分配模型。由于泊位分配与装卸桥调度相互影响，船舶作业时间在很大程度上取决于装卸桥的分配，而装卸桥的调度也要依据泊位计划，受泊位计划的约束。因此，一些研究关注泊位与装卸桥的集成调度问题。如Park和Kim[7]建立了同时优化船舶停泊位置、停泊时间、以及装卸桥配置的混合整数规划模型。Imai等[8]采用离散泊位分配方法，建立了泊位计划与装卸桥调度模型。Liang等[9]建立了泊位分配-装卸桥调度模型，与前两个模型不同的是，模型中考虑了装卸桥配置数量对装卸桥平均作业效率的影响。

上述研究主要面向确定性环境，近年来，不确定性环境下泊位与装卸桥调度问题受到越来越多的关注。一种方法是在泊位计划阶段，通过考虑不确定性因素，提高调度方案抵御不确定性干扰的能力。如，Han等[10]考虑船舶到达时间、装卸桥作业时间不确定性的基础上，建立了泊位分配-装卸桥调度模型，目的是获得泊位与装卸桥的鲁棒调度方案。周鹏飞和康海贵[11]基于随机规划方法，构建了随机环境下泊位-岸桥分配模型。Zhen和Chang[12]建立的泊位分配的多目标模型，同时优化作业成本和泊位计划的鲁棒性。另一种方法是研究不确定性干扰事件发生后，如何调整泊位计划，以减小干扰事件的影响。如曾庆成等[13]分析了干扰事件对泊位分配与装卸桥调度的影响，建立了集装箱码头泊位分配-装卸桥调度的干扰管理模型。

虽然这两种方法分别从事前与事后角度处理不确定性因素，但事实上，二者是相互联系的。如在泊位计划制定阶段，可以通过提高鲁棒性，减低方案调整的难度和调整的成本；而干扰事件的分析与评价，也有利于鲁棒调度策略的制定。鲁棒调度作为研究不确定环境下生产调度问题的一种重要方法，近年来受到国内外学者的广泛关注，出现了大量的研究成果(Wu等[14])，但由于不同鲁棒调度问题差异较大，其鲁棒调度模型与策略存在较大差异。尽管泊位计划鲁棒调度已有一些研究成果(Han等[10])，但泊位计划的鲁棒性度量、以及泊位计划鲁棒性与成本之间的权衡等问题还需要进一步研究，这些都是泊位计划鲁棒调度中的关键问题。

2 泊位分配模型

采用连续型泊位分配方法，同时优化泊位分配与装卸桥调度计划，即优化每艘船舶的停泊位置、停靠时间、以及装卸桥配置数量。模型参数与变量假设如下：

模型参数：

L：泊位岸线总长度，将岸线划分为若干以10米为单位的单元；

N：一定时期内停靠船舶的总数；

Q：装卸桥配置总数；

T：以小时为单位的若干时间点的集合；

ai：船舶i预计到港时间；

di：船舶i预计离港时间，此时间通常由船公司与码头协议确定；

li：船舶i的长度，以10米单元数量表示；

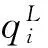
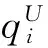
wi：完成船舶i作业需要的装卸桥总台时数；

M：一足够大的常数。

决策变量：

xi：船舶i的停靠位置；

yi：船舶i的停靠时间；

ei:船舶i作业完成时间；

假设泊位水深能充分满足船舶停靠要求，装卸桥单位作业效率不受同时作业装卸桥数量的影响。于是，泊位分配模型可以表示为：

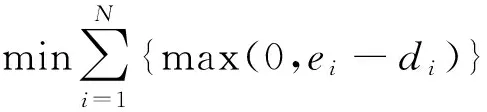
(1)

(2)

(3)

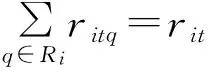
(4)

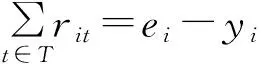
(5)

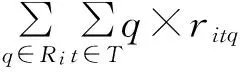
(6)

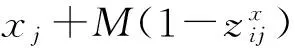
(7)

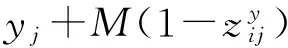
(8)

yi≥ai,∀i=1,…,N

(9)

xi∈{0,1,…,L-li},∀i=1,…,N

(10)

(11)

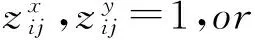
(12)

式(1)为目标函数，表示最小化船舶延误时间。式(2)表示装卸桥数量约束，式(3)避免两艘船舶之间在停靠时间与停靠位置上的冲突，式(4)～(6)表示每艘船舶作业开始与结束时间的关系，式(7)表示两艘船舶停靠位置之间的关系，式(8)表示两艘船舶停靠时间的关系，式(9)保证每艘船舶在其到港时间之后停靠，式(10)保证每艘船均停靠在岸线范围内，式(11)表示分配给每艘船舶的最大与最小装卸桥数。

3 泊位计划鲁棒性度量

3.1 鲁棒性度量指标

鲁棒性度量是优化鲁棒调度方案的基础，在优化调度方案时，通过优化鲁棒性度量指标，可以提高调度方案吸收不确定性干扰的能力。目前，机器调度领域的鲁棒性度量问题得到了较多的研究[15]，主要的方法包括基于后悔值、最差情景、领域度量、松弛度量等方法。本文基于松弛度量方法，提出以下泊位计划鲁棒性的度量指标：

(1)平均松弛

在泊位计划中，某一艘船舶作业的松弛量定义为在不影响后续船舶作业开始时间的前提下，其作业开始时间的最大延误量。

si=LSi-ESi

(13)

其中，si表示在泊位计划中，船舶i的松弛量，ESi表示船舶i作业最早开始时间，LSi表示在不影响后续船舶的情况下，船舶i作业最晚开始时间。于是，泊位计划的松弛量可以表示为：

(14)

(2)权重松弛量

RM1假定每艘船舶具有相同的权重，事实上，后续作业任务多的船舶，其延误造成的影响大于后续作业任务较少的船舶，因此，用权重松弛量考虑后续作业船舶量的影响：

(15)

其中，NSi表示船舶i的后续作业船舶数，可以表示为：

(16)

另外，可以以船舶的作业量作为权重，设置一下两个指标：

(17)

(18)

(3)松弛函数

上述4个度量指标假设每单位的松弛量的边际影响相同，这可能会过分高估某些任务松弛的影响，尤其是当某作业任务松弛量非常大时。为此，采用松弛效用函数度量，即：

(19)

同时，可以采用有效松弛量度量(RM6)，其中，frac表示比例系数。当某一作业任务的松弛量较小时，将其计算到总松弛量中，而当某一作业任务松弛量较大时，只将其潜在的有效部分计算到总松弛量中，即：

(20)

另外，以0-1(αi)变量代替si进行度量，当泊位计划中船舶i存在松弛量时，αi=1，否则=0。其计算公式如式(21)所示：

(21)

(4)其它指标

另外，结合按照以上方法，设置以下指标：

(22)

(23)

(24)

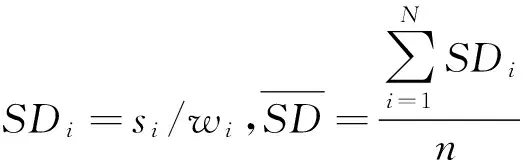
3.2 指标评价方法

首先，对于通过泊位分配模型(1)～(12)获得的泊位计划方案，计算其船舶总延误时间(即计划延误时间)。然后，利用模特卡罗发生成多个仿真情景，计算这些情景下船舶总延误时间(即实际延误时间)，以及鲁棒性指标RMi(i=1,…,10)。最后，计算鲁棒性指标与PM1,PM2之间的相关性，选择相关性大的指标作为泊位计划鲁棒性度量指标。

其中，PM1表示在所有的仿真情景中，船舶实际延误小于计划延误的比例，即，PM1=(实际延误大于计划延误的情景)/情景总数；PM2表示船舶实际延误与计划延误之间的差异，即，PM2=(平均实际延误-计划延误)/计划延误

具体评价方法过程如下：

(1)泊位分配方案产生

按照以上方法产生Nf个泊位分配方案，计算每个方案的鲁棒性指标值RMi(i=1,…,10)。

(2)蒙特卡罗仿真

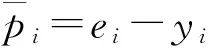
重复此步骤Nr次。

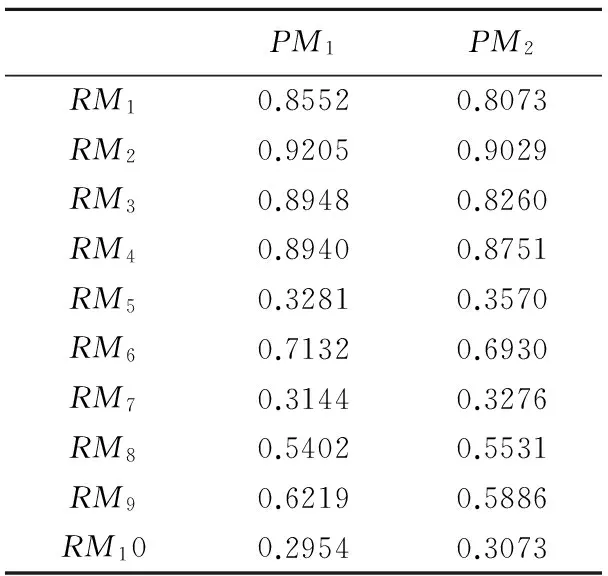
表1 RMi与PMi之间相关性(R2)

(3)相关性计算

计算上述步骤产生的Nr×Nf个情景的PM1，PM2以及RMi(i=1,…,10)与PM1,PM2的相关性，选择相关性大的RMi作为泊位计划鲁棒性度量指标。

3.3 评价结果

选择天津某集装箱码头7天船舶到港数据(共有22艘到港船舶)进行分析，此码头岸线长度1202米，共配置装卸桥12台，装卸桥平均效率为30次/小时。假设Nf,Nr分别为20次、30次，步长Δ为0.01，frac为0.1。计算得到RMi与PMi之间的决定系数(R2)如表1所示。

结果表明，RM2具有最大的决定系数R2，另外，RM1,RM3,RM4也与PMi之间具有较高的相关性。

4 泊位计划的鲁棒优化算法

4.1 算法设计

选择与PMi相关性最大的指标RM2泊位计划鲁棒性的度量指标，通过最大化RM2获得鲁棒调度方案，其优化过程通过两阶段算法实现：

(1)第一阶段

不考虑泊位计划的鲁棒性，以船舶总延误时间(Cmax)最小为目标函数优化泊位计划，即通过求解式(1)～(12)获得泊位计划方案。

(2)第二阶段

鲁棒性度量指标RM2最大化为目标函数，以第一阶段获得的船舶总延误时间Cmax以及式(2)～(12)为约束条件，获得鲁棒调度方案。

同等条件下，作业资源(如装卸桥数量)的增加会使RM2增加，从而提高调度方案的鲁棒性。为了提高调度方案的鲁棒性，在第二阶段求解中，考虑变化装卸桥数量，即Q=(1+η)Q0。另一方面，装卸桥的增加会增加作业成本，需要在调度方案的鲁棒性与作业成本之间做出平衡。为此，通过变化装卸桥数量，分析装卸桥配置数量与泊位计划鲁棒性RM2，以及泊位计划实施效果PM1的关系。以第一阶段获得的Cmax为约束，通过变化装卸桥数量分析，可以为实际调度人员平衡鲁棒性和作业成本间的关系提供依据。

在算法第一、二阶段，分别采用基于拉格朗日松弛的算法求解，式(1)～(12)模型的拉格朗日松弛表述为：

(25)

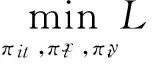
(27)

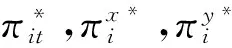
4.2 算例分析

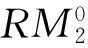
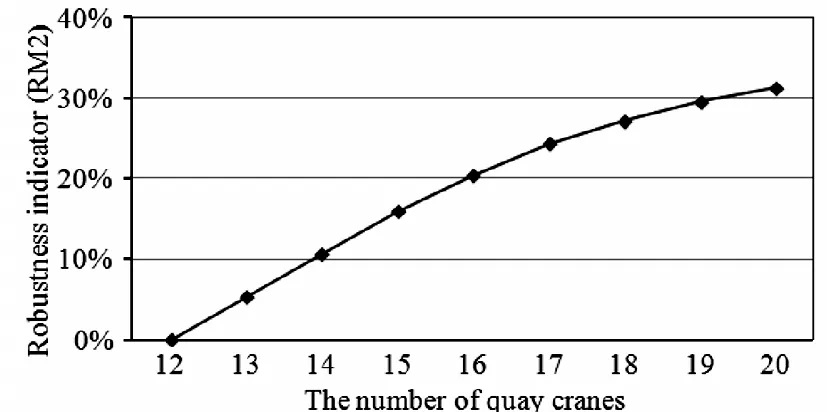
图1 装卸桥数量与泊位计划鲁棒性关系

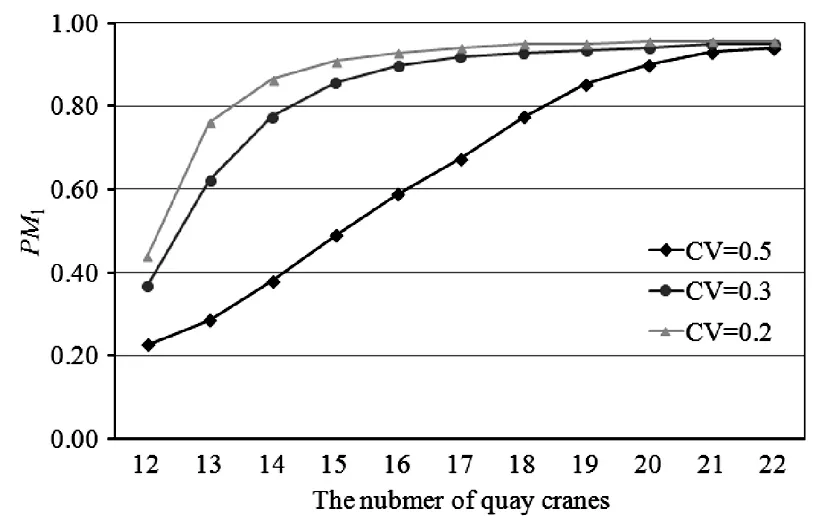
图2 装卸桥数量与泊位计划方案效果关系

其次，分析装卸桥配置数量与泊位计划方案效果(采用指标PM1度量)的关系，通过两阶段算法，获得不同装卸桥数量情况下的泊位计划方案，分别假设船舶作业时间的变异系数CV等于0.5、0.3、0.2，计算PM1，得到图2所示的结果。

从图2可以看出，随着装卸桥数量的增加，泊位计划方案的PM1值随之增加，即船舶按照泊位计划完成作业的比例增加。这说明，装卸桥数量的增加，提高了泊位计划的鲁棒性。另一方面，随着装卸桥数量的继续增加，PM1值改进的速度越来越慢。

在实际应用中，决策者需要在作业资源投入与泊位计划鲁棒性之间做出平衡。这里，以下模型决定装卸桥投入数量：

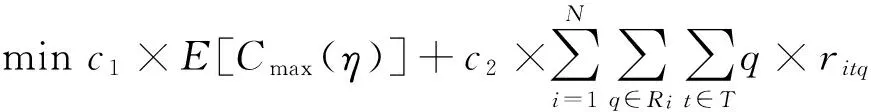
(28)

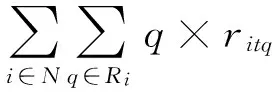
(29)

其中，c1表示如果船舶没有在规定时间完成作业，其单位延误时间的惩罚成本，c2表示装卸桥单位台时的成本，E[Cmax(η)]表示在投入Q0(1+η)台装卸桥情况下，考虑船舶作业时间的不确定性，船舶延误时间的期望值。由于装卸桥数量为整数值，因此这里η为离散变量，即Q0(1+η)为整数的取值。

假设c2=5000元/艘，c2为1300元/小时。在实际中，c2结合集装箱码头与船公司签订的作业合同确定。利用图2中数据计算可得，CV取值0.5时，最优装卸桥配置数量分为17台，CV取值0.3与0.2时，装卸桥配置数量为15台。

5 结论

为了降低不确定性因素对集装箱码头船舶作业系统的影响，研究泊位计划鲁棒性度量与优化问题，提出了泊位计划鲁棒性的度量方法，设计了泊位计划鲁棒优化的两阶段优化算法，分析了研究作业资源的变化对调度方案鲁棒性的影响。方案的鲁棒性度量是鲁棒调度的关键问题之一，本文为泊位计划的鲁棒性度量提供了一种有效方法，为集装箱码头计划制定者如何平衡作业成本与调度方案鲁棒性提供了新思路，有助于拓展鲁棒优化应用领域。实际应用方面，提出了通过装卸桥数量变化调整调度方案鲁棒性的方法，实际应用时，可根据码头自身资源状况灵活选择鲁棒性策略，模型的实用性更强。

本文在优化泊位计划只考虑泊位计划的鲁棒性，以及装卸桥配置数量对鲁棒性的影响。没有考虑装卸桥调度(即装卸桥在泊位前沿以及不同作业船舶间的移动路径)鲁棒性的影响。事实上，装卸桥的调度直接影响泊位计划的实施，因此，装卸桥调度鲁棒性也会影响泊位计划的鲁棒性，二者之间的影响与相互关系是值得进一步研究的问题。

[1] Nishimura E, Imai A, Stratos P. Berth allocation planning in the public berth system by genetic algorithms[J]. European Journal of Operational Research, 2001, 131(2): 282-292.

[2] Imai A, Nishimura E, Stratos P. Berth allocation with service priority[J]. Transportation Research Part B, 2003, 37(5): 437- 457.

[3] Kim K H, Moon K C. Berth scheduling by simulated annealing[J]. Transportation Research Part B, 2003, 37(6): 541-560.

[4] Imai A, Sun X, Nishimura E et al. Berth allocation in a container port: using a continuous location space approach[J]. Transportation Research Part B, 2005, 39(3): 179-221.

[5] Imai A, Nishimura E, Hattori M, et al. Berth allocation at indented berths for mega-containervessels[J]. European Journal of Operational Research, 2007, 179(2): 579-593.

[6] Wang F, Lim A. A stochastic beam search for the berth allocation problem[J]. Decision Support Systems, 2007, 42(4): 2186-2196.

[7] Park Y M, Kim K H. A scheduling method for berth and quay cranes[J]. OR Spectrum, 2003, 25(1): 1-23.

[8] Imai A, Chen H C, Nishimura E, et al. The simultaneous berth and quay crane allocation problem[J]. Transportation Research Part E, 2008, 44(5): 900-920.

[9] Liang C, Huang Y, Yang Y. A quay crane dynamic scheduling problem by hybrid evolutionary algorithm for berth allocation planning[J]. Computers & Industrial Engineering, 2009, 56(3): 1021-1028.

[10] Han X L, Lu Z Q, Xi L F. A proactive approach for simultaneous berth and quay crane scheduling problem with stochastic arrival and handling time[J]. European Journal of Operational Research, 2010, 207(3): 1327-1340.

[11] 周鹏飞,康海贵.面向随机环境的集装箱码头泊位-岸桥分配方法[J].系统工程理论与实践,2008,28(1):161-169.

[12] Zhen L, Chang D F. A bi-objective model for robust berth allocation scheduling[J]. Coputers & Industrial Engineering, 2012; 63(1): 262-273.

[13] 曾庆成,胡祥培,杨忠振.集装箱码头泊位分配-装卸桥调度干扰管理模型[J].系统工程理论与实践,2010,30(11):2026-2035.

[14] Wu C W, Brown K N, Beck J C. Scheduling with uncertain durations: modeling-robust scheduling with constraints[J]. Computers & Operations Research, 2009, 36(8): 2348-2356.

[15] Goren S, Sabuncuoglu I. Robustness and stability measures for scheduling: single machine environment[J]. IIE Transactions, 2008, 40: 66- 83.

[16] Held M, Wolfe P, Crowder H P. Validation of sub-gradient optimization[J]. Mathematical Programming, 1974, 6: 62- 88.

Robust Optimization Model for Berth Planning Problem in Container Terminals

ZENG Qing-cheng1, ZHAO Xiao-feng1, HU Xiang-pei2, YANG Zhong-zhen1

(1.SchoolofTransportManagement,DalianMaritimeUniversity,Dalian116026,China; 2.InstituteofSystemsEngineering,DalianUniversityofTechnology,Dalian116023,China)

To tackle the uncertainties that happen in operations of container terminals, robust optimization model and algorithms for berth planning problem are developed. The objective is to decrease the impact of uncertainties on operation efficiency of container terminals. Firstly, the robustness measures for berth schedule are proposed, and the each measure is assessed through computational experiments. Then, a two-stage robust optimization algorithm is designed: the first stage is to minimize the total delay of berthing vessels without considering the schedule robustness, and the total delay obtained is taken as a threshold value for the next stage. The second stage is to maximize the robustness measures while keeping the total vessel delay at a level equal to or smaller than the threshold value obtained by the first stage. Finally, the impact of operation resource(the number of quay cranes)on schedule robustness is analyzed. Numerical experiments indicate that weighted slack index is a valid robustness measure and the proposed two-stage algorithm can solve the robust optimization of berth plan efficiently.

logistics engineering; berth planning; robust optimization; container terminals

2012- 08-10

国家自然科学基金资助项目(71001012, 71370137)；教育部“新世纪优秀人才支持计划”(NCET-11- 0859)

曾庆成 (1978-)，男，教授，工学博士，研究方向，港口与物流系统优化。

U691

A

1007-3221(2015)02- 0071- 07