需求信息不对称下多渠道供应链的协调定价
于丽娟, 李 雪, 祝爱民
(沈阳工业大学 管理学院,辽宁 沈阳 110870)
需求信息不对称下多渠道供应链的协调定价
于丽娟, 李 雪, 祝爱民
(沈阳工业大学 管理学院,辽宁 沈阳 110870)
针对由一个制造商和一个零售商组成的两层供应链,其中制造商拥有网络直销渠道和传统零售渠道组成的多渠道问题,运用stackelberg博弈分别进行了制造商和零售商需求信息不对称时二者集中控制和分散控制时的最优定价分析,结果表明分散控制会降低供应链的总体效率,继而为了提高多渠道供应链的效率,通过数量折扣模型对多渠道供应链进行协调定价,最后进行了算例验证及有效性分析,结果表明数量折扣模型能使多渠道供应链中的制造商和传统零售商达到双赢,它是合理有效的。
企业管理;协调定价;stackelberg博弈;数量折扣;需求信息不对称;多渠道供应链
0 引言
近年来电子商务的广泛应用带来了网络直销的飞快发展,很多企业开始在原有的传统零售渠道的基础上增加网络直销渠道,形成多渠道。但是采用多渠道以后,制造商与零售商之间不仅存在传统意义下的纵向竞争,而且渠道之间还存在各种形式的横向竞争, 由此导致的激烈的渠道冲突会影响整个供应链系统的效率。因此如何对多渠道供应链定价才能提高供应链效率引起了学术界和企业界的广泛关注。
国内外学者对于完全信息下多渠道供应链的定价研究主要集中在对电子商务零售商与传统零售商的价格竞争研究[1~4]、减少或者避免多渠道冲突的价格策略及不同价格策略下制造商和零售商的利润[5,6]以及基于消费者效用理论、动态博弈模型等对多渠道供应链中制造商、零售商的最优定价、均衡定价、均衡利润[7~9]等方面研究取得了一些有价值的成果。
在实际的非一体化供应链中, 各成员之间可能拥有不对称的信息, 对非对称信息下多渠道供应链的定价研究更具有复杂性和现实性。以往的相关研究主要集中在成本、价格、风险规避等信息不对称下的最优定价以及信息分享对绩效的影响[10~13]等方面。却很少对信息不对称下多渠道供应链进行协调定价。在传统渠道研究领域,学者们从库存、价格、订货、竞争、合同等不同角度提出了多种渠道协调机制,其中最常见的是价格机制,主要为数量折扣。本文对需求信息不对称下多渠道供应链中制造商和零售商的定价问题进行协调性分析,并进一步通过数量折扣模型[14]来协调制造商和零售商之间的合作,提高供应链的总体效率。
1 基本模型与记号
本文考虑的由一个制造商和一个零售商组成的供应链中制造商只向零售商提供一种产品,其中制造商不仅通过传统零售商销售产品,而且还开通网络直销渠道直接向消费者销售相同的产品,传统零售渠道和网络直销渠道组成多渠道。假设传统零售商相对比较弱势,只能从制造商而不能从直销渠道处订购商品。需求函数由确定性需求部分和随机需求部分组成,表示为Q(p)+q[15],且Q(p)≥0,其中确定性需求部分采用线性需求函数,假设为
Qd=(θ+ρ)ma-Pd+b(Pr-Pd),Qr=(1-θ)ma+(1-m)a-Pr+b(Pd-Pr)
Pd,Pr分别表示直销渠道和零售渠道中产品的零售价;Qd,Qr表示直销渠道和零售渠道的市场需求;a为大于零的常数,表示只有单一零售渠道时总的市场规模;m是电子商务实施程度,表示所有顾客中能够上网的人数比例;θ表示增加直销渠道以后具有上网条件的顾客中选择网络购买的比例;ρ表示直销渠道所带来的潜在需求比例;b∈(0,1),是直销渠道与零售渠道的替代效用系数。

本文主要研究需求信息不对称下供应链中制造商和零售商的定价问题。假设零售商比制造商知道更多的需求信息,即qr对于零售商来说是确定的。由于在我国网络营销还不够成熟,所以假设制造商不知道qd的确定值。除此之外,需求分布,成本等信息都是双方的共同知识。同时假设制造商和零售商都是风险中性的。
定义其他变量符号:字母上方标有‘—’表示期望,字母右上方标有‘1’‘*’分别表示经过了量折扣和最优解。
c制造商生产一单位产品的成本;c1、c2分别表示直销渠道和传统零售渠道销售一单位产品的成本;PD、PR分别表示集中控制时直销渠道和零售渠道中产品的价格;Πm、Πr分别表示分散控制时制造商和零售商的利润;Πc,ΠC分别表示分散控制和集中控制时系统的总利润;ω1、Q1量折扣的批发价格和资格订购量。
2 协调定价的必要性分析
2.1 分散控制时的定价问题
此时制造商和零售商各自独立定价,二者都是利润最大化者。它们之间形成了一个stackelberg博弈,制造商是主导者,零售商是跟随者,博弈的顺序是:首先制造商确定最优批发价和网络直销价格,然后零售商根据制造商的定价和观测到的需求量qr确定最优的零售价格以及订货数量。求解的时候采取逆向递推法,先考虑零售商的问题:Πr=(Pr-ω-c2)(Qr+qr)。
零售商知道qr的确切的值,由一阶和二阶最优条件得:
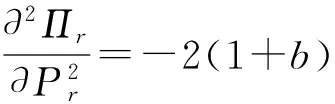
(1)
由一阶最优条件得:
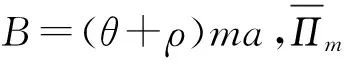
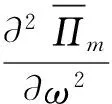
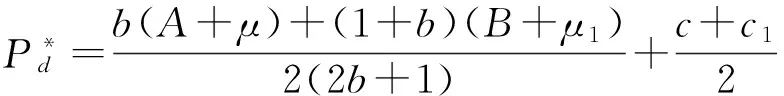
(2)
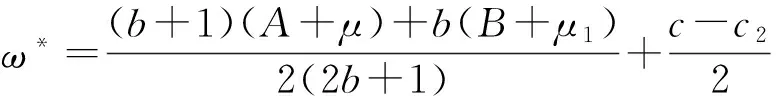
(3)
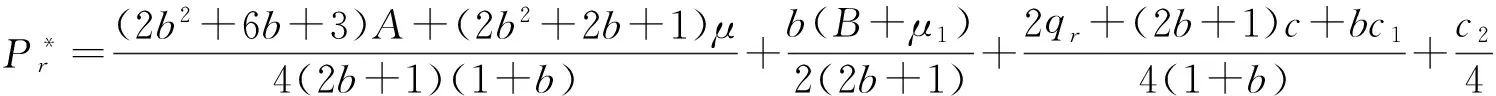
(4)

(5)

(6)
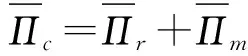
(7)
由以上得到的制造商和零售商的期望利润可以得到定理1:
定理1 零售商的期望利润与随机市场需求部分的波动大小有关,但是制造商的期望利润与随机市场需求部分的波动大小无关。
2.2 集中控制时的定价问题
当对制造商和零售商进行集中控制时,零售商会分享不确定需求部分qr的值,这种情况下供应链的目标函数就变成总的利润最大化:
ΠC=(PR-c-c2)(Qr+qr)+(PD-c-c1)(Qd+qd)
由一阶最优条件得:
ΠC的Hessian矩阵为:
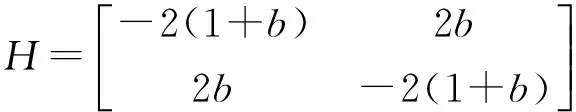

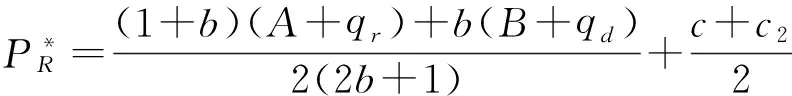
(8)
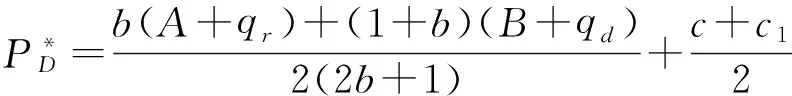
(9)
(10)
(11)
3 数量折扣协调定价
数量折扣在供应链协调管理中是被广泛应用的一种协调机制。制造商可以通过提供数量折扣计划来诱使零售商订购更多的产品,进而增加自己的利润,这里采用一种简单的数量折扣的设计方法。假设制造商提出折扣计划(Q1,ω1),即
如果零售商订购量小于Q1,制造商提供正常批发价格ω*;
如果零售商订购量不小于订购量Q1,制造商提供折扣批发价格ω1。
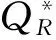
由一阶和二阶最优条件得:
由此可得批发价为ω1时,制造商的最优直销价格为:
(12)
即而可得零售商的最优零售价格和最优订货量:
(13)
(14)
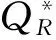
(15)
(16)
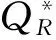
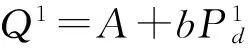
(17)
这种情况下零售商和制造商的利润分别为:
(18)
(19)
②零售商不考虑量折扣的批发价,此时制造商提供的批发价是ω*,零售商和制造商的利润分别为:
(20)
(21)

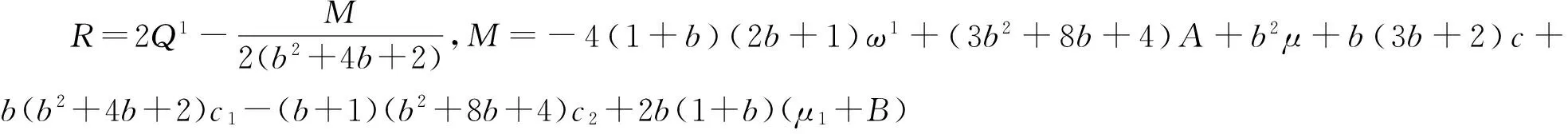
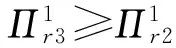
总结以上内容,可以得到:
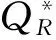
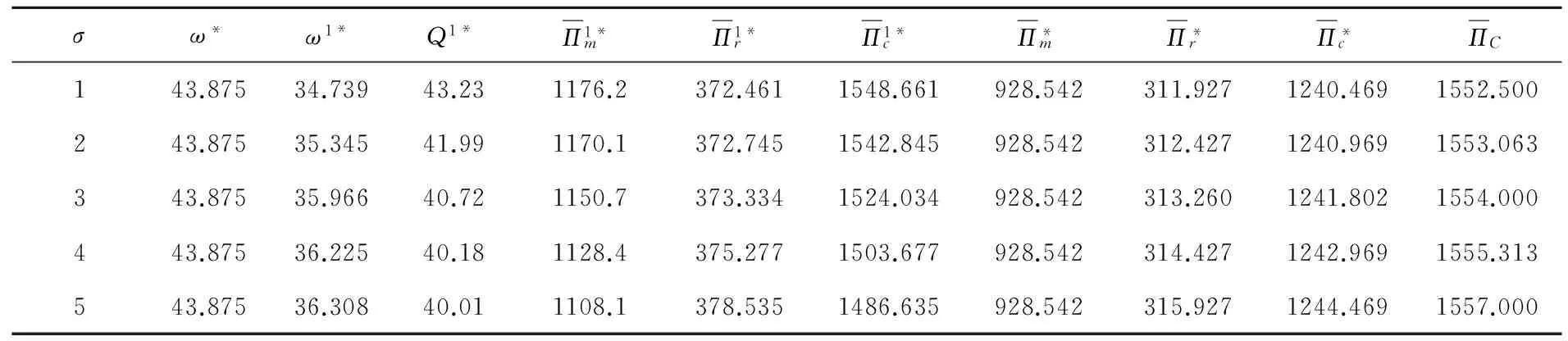
当qr∈S1≡{qr 当qr∈S2≡{qr 因此在数量折扣计划下,制造商的期望利润是: (22) 接下来要确定Q1和ω1的最优值,即要求出使制造商期望利润最大的(Q1*,ω1*),就是要解决优化问题: (23) 然后可以得到零售商在最优量折扣计划(Q1*,ω1*)下的最终期望利润: (24) 这个量折扣模型可以通过(23)式求出最优解,但是由于(23)式的复杂性,这里不能提供模型的分析最优解,但是可以通过下面的方法求出其数字最优解。 (2)利用复合形法求出最优的数字解(Q1*,ω1*)。 将各数值代入相应的公式,可以得到:采取量折扣计划之前,制造商和零售商分散控制时,制造商设定的最优批发价格ω*=43.875、零售商的期望订购量为21.625。 对于制造商提出的量折扣计划,根据(22)、(23)式,通过MATLAB软件可以求出(Q1,ω1)的最优数字解为Q1*=43.226,ω1*=34.739,即制造商提出的量折扣计划为: 如果零售商订购量小于43.226,制造商提供批发价格43.875; 如果零售商订购量不小于43.226,制造商提供批发价格34.739。 考察参数m和σ的变化对量折扣计划和双方期望利润的影响,令m以步长0.05从0.3变化到0.5;σ以步长1从1变化到5(其他的参数保持不变),然后分别求出最优解,结果列于表1、表2中。 表1 参数m变化对最优解的影响 由表1可知,电子商务实施程度m变大时,最优批发价格降低,量折扣计划的资格订货量减少,制造商的最大期望利润加大,传统零售商的最大期望利润减小。这是因为电子商务实施程度越大,网络直销就会分享更大的市场份额,致使制造商的期望利润加大而传统零售商的期望利润减小,而制造商为了弥补传统零售商的损失,会相应的减少批发价格和降低零售商享受量折扣计划的门槛。 表2 参数σ变化对最优解的影响 由表2可知,当σ增大时,即传统零售市场需求不确定性增加时,最优批发价格和制造商的最大期望利润都不变,它们都不依赖于σ。量折扣计划的资格订购量下降,量折扣计划之后的制造商最大期望利润减小,零售商最大期望利润增加,这可能是由于市场需求不确定性增大,零售商面临的风险就增大,制造商通过降低量折扣计划的资格订购量来吸引零售商冒这个风险。 同时将表1、表2中量折扣计划前后制造商、零售商及整个供应链的期望利润进行对比,可知量折扣计划提高了它们的利润,则此量折扣计划是合理的。 本文分析了需求信息不对称下多渠道供应链中的制造商,传统零售商在分散控制及集中控制时如何定价的问题。通过一个量折扣模型来协调定价,提高整个供应链的效率。并进行了算例验证,结果表明这个量折扣计划模型能够提高制造商和传统零售商的利润,是合理可行的。 但是这里仅分析了由一个制造商和一个零售商组成的两层供应链的情形,考虑的比较简单,具有一定的局限性,可将问题推广到多零售商或者多层供应链的较复杂的情形上。 [1] Friberg R, Ganslandt M, Sandstrom M. Pricing strategies in e-commerce: bricks vs. click[R]. Working paper, Stockholm School of Economics, Sweden, 2001. 559-582. [2] Pan X, Shankar V, Ratchford B T. Price competition between pure play vs. bricks-and-clicks e-tailers: Analytical model and empirical analysis[R]. Working paper, Smith School of Business, University of Maryland, 2002. 29- 61. [3] 蔡津,张正华.基于博弈论的电子商务零售商与传统零售商的价格竞争模型[J].上海理工大学学报,2001,23(1):71-74. [4] 陈云,王浣尘,沈惠璋.电子商务零售商与传统零售商的价格竞争研究[J].系统工程理论与实践, 2006,23(1):35- 41. [5] Cattani K D, Gilland W G, Swaminathan J M. Coordinating traditional and internet supply chains[A]. Simchi-Levi D, Wu D, Shen M,(eds.) .Supply chain analysis in the ebusiness era[C].Kluwer Academic Publishers, Boston, MA, 2004. 643- 675. [6] Cattani K, Gilland W, Heese H S. Boiling frogs: pricing strategies for a manufacturer adding a direct channel that competes with the traditional channel[J]. Production and Operations Management, 2006, 15(1): 40-56. [7] Chiang W K, Chhajed D, Hess J D. Direct marketing, indirect profits: a strategic analysis of dual channel supply-Chain design[J]. Management Science, 2003, 49(1): 1-20. [8] Yao D Q, Liu J J. Competitive pricing of mixed retail and e-tail distribution channels[J]. Omega, 2005, 33(3): 235-247. [9] Dumrongsiri A, Fan M, Jain A, et al.. A supply Chain model with direct and retail channels[J]. European Journal of Operational Research. 2008, 187(3): 691-718. [10] Mukhopadhyay S K, Yao D Q, Yue X H. Information sharing of value-adding retailer in a mixed channel Hi-tech supply Chain[J]. Journal of Business Research. 2008, 61(9): 950-958. [11] Li L. Information sharing in a supply chain with horizontal competition[J]. Management Science, 2002, 48(9): 1196-1212. [12] 艾兴政,唐小我,马永开.传统渠道与电子渠道预测信息分享的绩效研究[J].管理科学学报,2008,11(1):12-21. [13] 王虹,倪卫涛,周晶.非对称信息下双渠道供应链的定价决策[J].管理学报,2010,7(2):238-242. [14] 周永务,杨善林.基于不对称需求信息的供应链协调定价[J].系统工程学报,2006,21(6):591-597. [15] 李爱国,覃征,鲍复民.粒子群优化算法[J].计算机工程与应用,2002,38(21):1-3. Coordination Pricing in Multi-channels Supply Chain with Asymmetric Demand Information YU Li-juan, LI Xue, ZHU Ai-min (SchoolofManagement,ShenyangUniversityofTechnology,Shenyang110870,China) In recent years, with e-commerce widely used, direct channel has been developed fastly. Many enterprises begin to increase direct channel on the basis of traditional retailing channel. To the problem of one-manufacturer one-retailer supply chain with asymmetric demand information between the two members,the manufacturer owns multi-channels composed by direct channel and traditional retailing channel. This paper analyzes the optimal wholesale price of the manufacturer and retailer when they centralize control and decentralized control with stackelberg Game Theory separately, and the result shows that decentralized control can lower the efficiency of the supply chain. To improve the efficiency of the multi-channels supply chain, we provide the manufacturer with a quantity-discount pricing policy that can coordinate the multi-channels supply chain price. Lastly we use the numerical test and effectiveness analysis, and the result shows that quantity-discount can make the manufacturer and retailer in the supply chain win-win, so it is reasonable and effective. business management; coordination pricing; stackelberg game; quantity-discount; asymmetric demand information; multi-channels supply chain 2012- 06-19 辽宁省科技计划重点项目(2010401037) 于丽娟(1970-),女,副教授,硕士生导师,研究方向:战略管理与市场营销。 F274 A 1007-3221(2015)02- 0044- 07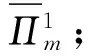
4 算例验证和有效性分析
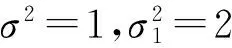


5 结束语

