Vague指派问题的求解方法研究
崔春生
(1.河南财经政法大学 计算机与信息工程学院,河南 郑州 450002; 2.中国社会科学院 数量经济与技术经济研究所,北京 100010)
Vague指派问题的求解方法研究
崔春生1,2
(1.河南财经政法大学 计算机与信息工程学院,河南 郑州 450002; 2.中国社会科学院 数量经济与技术经济研究所,北京 100010)
Vague指派问题的特殊性在于用Vague值表述效益矩阵,进而反映了指派问题中存在的诸多不确定性和模糊性。论文根据Vague值的特点,提出了Vague指派问题的求解转化为经典指派问题思想,进而借助“马太效应”函数、特征值向量和Pareto三种方法实现问题的求解。最后,论文以参考文献中的一组数据为例,采用以上方法进行计算,得到了理想的结果。
运筹学;Vague指派;记分函数;特征值;Pareto
0 引言
指派问题是运筹学中一类特殊的线性规划问题,用于解决如何分派n个人去完成企业中n个不同的任务,以获得最佳的工作效率。指派问题中的效益矩阵代表每个人完成不同工作花费的时间,属于极小化问题,如果效益矩阵的含义有所变化,变成每个人完成不同工作得到的收益,指派问题就变成求目标函数极大的问题。
一般的,指派问题的数学模型可以表示为[1]:
(1)
其中,目标函数的系数cij≥0(i,j=1,2,…,n)。
通常,把这些数写成矩阵形式:
C称为系数矩阵或效益矩阵。
指派问题的形式很多,平衡指派问题研究人数与任务数相等,一人一事且一事一人。这种问题可以借助于匈牙利法[1]、削高排除法[2]、缩阵分析法[3]和差额法[4]等进行求解。广义指派问题也有很多形式,如人数大于事数,一人一事且一事多人;事数大于人数,一事一人且一人多事[5];实际分配任务数不超过总人数也不超过总任务数的C指派间题[6]。这些问题一般需要转换成平衡指派问题进行求解。
运筹学教材中的指派问题一般是在Canter集上求解,效益矩阵用实数来表示;模糊数学中运用Fuzzy集解决指派问题,效益矩阵中用模糊数刻画每个工作人员完成每项任务的熟练程度或满意程度[7]。吴祈宗等人[8]提出了Vague指派的思想,借助于记分函数方法实现了Vague值向实数值的转化。但是,记分函数在处理指派问题时并不能完全表达指派目标函数中的最小值的思想,因此有必要进一步探讨Vague指派的方法。
1 Vague指派问题的描述
Vague指派是指效益矩阵中的每一个数均为Vague值,表征了每个人完成每项工作花费时间(或取得收益)的不确定性。不确定程度的大小反映在Vague值之间的差异。
Vague集来源于Fuzzy集,在Fuzzy集基础上,通过真隶属度和假隶属度引入,给出以区间形式表示的隶属程度——该区间能够同时给出支持证据和反对证据的程度,并且能够表示中立的程度,从而提出Vague集的概念。Vague集较模糊集在描述客观事物时更贴近现实,更加形象[9,10]。
一个实数值Vague集A是由真隶属函数tA和假隶属函数fA描述的:
tA:U→[0,1],fA:U→[0,1]
对于x∈U,tA(x)是从支持的x∈A证据所导出的x∈A的肯定隶属度的下界,fA(x)是从反对x∈A的证据所导出的x∈A的否定隶属度的下界,并且tA(x)+fA(x)≤1。x关A的隶属度可由[0,1]上的子区间[tA(x),1-fA(x)]表示,或者称[tA(x),1-fA(x)]是在Vague集A中的Vague值。πA=1-tA(x)-fA(x)为关于A的未知度,也称为犹豫度或踌躇度。πA是相对于的未知信息的度量,πA的值越大,说明x相对于A的未知信息越多。当tA=1-fA时,πA=0,即tA+fA=1时,Vague值x退化为普通模糊值。
在Vague指派当中,肯定隶属度是乐观工作效率的表征,否定隶属度是悲观工作时间的表征,而未知度反映了工作效率的确定性程度。进而Vague指派的数学模型可以表示为:
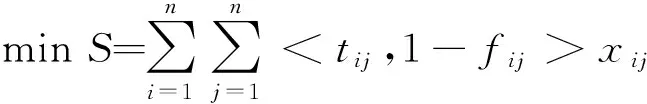
(2)
2 Vague指派的转化
通常来讲,Vague指派问题的求解可以有三种思路:
第一,指派问题的本质是求解最小化的线性规划问题,同时也是特殊的整数规划、0-1规划,还是需求量和供应量均为1的特殊运输问题,所以,可以采用Vague线性规划以及Vague运输问题的求解方法[11]。
第二,Vague值的核心是一种概率的思想,其表现形式类似于区间数,因而可以将其看成是一种特殊的区间数,采用区间数指派问题[12]的求解方法。
第三,Vague指派问题求解的一般思路是将Vague值转化为一般的实数值进行求解。
鉴于第一和第二种情况已有论述此,论文采用第三种思路探讨Vague指派问题。
2.1 基于“马太效应”的Vague值转化
Vague集中记分函数[13]表示了支持证据和反对证据之间的力量对比,主要用于相似度的计算。现实中,根据问题的不同性质,人们往往采取不同风险偏好的记分函数。即使是面对同一种事物,在不同的条件下,人们也会有不同的心态。例如,当支持证据占优时,更多采取激进乐观的策略;而当反对证据占优时,则尽可能地采取保守悲观的策略。
可见当支持证据占优时,记分函数满足:S(x)>S(Ex),容易采取风险追求型(Risk Proneness)记分函数[14]:
(3)
这种情况往往高估其真实值。
当反对证据占优时,记分函数满足:S(x) (4) 这种情况往往低估其真实值。 当反对证据和支持证据无法平衡时,记分函数满足S(x)=S(Ex),容易采取风险中立型(Risk Neutralness)记分函数,风险中立的记分函数就是Chen[13]提出的普通记分函数S(x)=tij-fij。 在指派问题的决策中,类似于其他社会现象,存在一种“马太效应”。所谓的“马太效应”(Matthew Effect)正是人们某种心理的反映——1968年,美国科学史研究者罗伯特·莫顿(Robert K. Merton)首次用“马太效应”来描述这种社会心理现象,“对已有相当声誉的科学家做出的贡献给予的荣誉越来越多,而对于那些还没有出名的科学家则不肯承认他们的成绩”。Vague集中的记分函数SME(x)则反映了这种价值取向[14]。 (5) 显然,“马太效应”中,tij>fij时是风险追求型的,在tij≤fij时是风险厌恶的。 2.2 基于特征向量的Vague值转化 从一般问题出发,考虑效益矩阵中Vague值的大小比较。显然,对Vague值比较,下列假设是合理的[15]: ①从肯定隶属度角度分析,tij越大,Vague值 ②从否定隶属度角度分析,1-fij越大(fij越小),Vague值 ③从未知度(也称犹豫度)角度分析,πi越小(1-πi越大),Vague值 目前,对于“一带一路”的传播思考仍然没能摆脱传统的思维框架,不少研究仍集中于“抢夺国际话语权”“讲好中国故事”等“自我中心论”。必须认识到,受欢迎的中国故事是能与当地受众建立起联系的故事。 对Vague集A={c11,c12,…,c1n,…,cnn},构造如下矩阵 (6) 其中Yl是含有m=n×n个分量的一维列向量,l=1,2,3。 设对应Vague集A={c11,c12,…,c1n,…,cnn}Vague值胡排序向量为O={O1,O2,…,Om}T,O>0。在上面给出的3个合理假设条件下,排序向量应该是所有的,具有m个分量的一维列向量中与矩阵Y的两个列向量的夹角之和最小的向量。因此如下定义Vague值的排序向量: 将Vague值的排序向量表示为O={O1,O2,…,Om}T,O>0,且不失一般性,令OOT=1。 定义2 令Z=YYT,称矩阵Z为Vague值排序矩阵。 定理2 排序矩阵是正矩阵,即Z>0。 定理3 Vague值排序矩阵Z的最大特征值对应的特征向量即为排序向量。 证明 令O∈Rm,O={O1,O2,…,Om}T,O>0且OOT=1。令 为求出f的最大值,建立辅助函数:g(O1,O2,…,Om,λ)OTYYTO-λ(OTO-1) 令 可知,如果f取最大值,则λ是Z的特征值,且O是Z的一个特征向量。 下面证明λ是Z的最大特征值[18]。 由定理2可知Z>0。由Perron定理知Z有最大特征值λ和λ对应的唯一特征向量O*满足O*TO*=1。令λ′是Z的另一个特征值,且λ≠λ′。 令对应于λ′的特征向量为O′,且O′TO′=1。有 λ≠λ′;ZO*=λO*,ZO′=λ′O′,O*TO*=1,O′TO′=1 用O*T左乘ZO*=λO*,用O′T左乘ZO′=λ′O′,有 O*TZO*=λO*TO*=λ,O′TZO′=λ′O′TO′λ′ 2.3 基于Pareto的Vague转化 Vague指派问题的线性规划模型(2)进一步表示为: (7) 可以证明,问题(7)的每一个Pareto解都是原问题(2)的一个有效解[19]。 引入参数λ,将问题(7)转化为参数规划问题: (8) 可以证明,对应于λ的最优解都是问题(7)的Pareto最优解[19]。 进而可以用目标区间的λ水平最优解作为原问题的满意解,其中λ可根据决策者的风险态度及当时的决策环境而定,当λ=1时,属于乐观型决策,风险较大;当λ=0时,属于悲观型决策,其追求的目标较低,往往会失去很多良机。 以论文[8]中RP1的为例,从新的研究内容出发,采用后两种方法进行计算。 3.1 基于特征向量 借助Matlab计算可得: 采用Matlab中的eig函数,得最大特征值为:λ=6.1510。 对应的特征向量为: OT=(0.2088 0.3309 0.3192 0.2844 0.1655 0.1248 0.2758 0.3106 0.2903)T 3.2 基于Pareto求解 Vague集在解决不确定性问题时具有自身的优点,可以更加形象的描述问题的本质,使得问题处理更加贴近实际,但是这一优点给问题的求解带来了诸多不便之处,因而论文着重探讨Vague值的转化问题。 在Vague指派问题中,论文中提出了三种方法。“马太效用”记分函数方法比较简单,并且具有一定的灵活性,一方面可以根据问题的不同性质采用风险追逐的记分函数和风险厌恶型函数进行数据处理;另一方面即使在同一个问题当中,可以根据不同的问题性质采用不同的记分函数,以取得更加科学的指派结果。基于特征向量的转换方法理论严谨,思路清晰,但是这种方法的基础是将Vague值看成区间数,如果将Vague值看成一种概率的思想则无法采用这种方法。基于Pareto的方法强调的是得到一个Pareto解而非最优解,实际上在不确定性信息环境下是不存在最优解的,因此这种方法的结果可能更加适合于解释Vague指派的思想。 [1] 吴祈宗,李光,崔春生.运筹学[M].广州:暨南大学出版社,2009. [2] 周良泽.削高排除法求解指派问题[J].系统工程学报,1992,7(2): 97-105. [3] 丁文仁.缩阵分析法—求解指派问题的新方法[J].系统工程理论与实践,1988,8(3):83- 86. [4] 周素琴.指派间题的新算法[J].上海师范大学学报(自然科学版),1997,26(2):38- 42. [5] 余英姿,张强.一类广义指派问题的有效解法[J].数学的实践与认识,2008,38(4): 86-92. [6] 白国仲,毛经中.C指派问题[J].系统工程理论与实践,2003,23(3):107-111. [7] 崔春生,吴祈宗.基于模糊数学的员工工作分配问题研究[C].南京:中国运筹学会第九届学术交流会,2008:603- 609. [8] 崔春生,吴祈宗.调剂问题的Vague指派方法研究[J].数学的实践与认识,2010,40(5):72-78. [9] Gau W L, Buehrer D J. Vague sets[J]. IEEE Transactions on Systems Man and Cybernetics, 1993, 23(2): 610- 614. [10] Atanassov K, Gargov G. Interval valued intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems. 1989, 31(3): 341-349. [11] 苏白云.一种运用Vague集理论转化区间运输规划的方法[J].数学的实践与认识,2013,43(4):97-99. [12] 刘小冬,张明海,臧振宇.区间指派问题的研究[J].西安财经学院学报,2011,24(1):19-22. [13] Chen S. Measure of similarity between vague sets[J]. Fuzzy sets and systems. 1995, 74(2): 217-223. [14] 王伟平,吴祈宗.关于Vague集理论中记分函数的分析[J].北京理工大学学报(自然科学版),2008,28(4):372-376. [15] 崔春生.基于集团序方法的推荐系统输出[J].系统工程理论与实践,2013,33(7):1845-1851. [16] 侯福均,廖爱红,吴祈宗.判断信息为偏好序的社会选择:特征向量法[J].南京理工大学学报(自然科学版),2008,32(12):80- 83. [17] 侯福均,吴祈宗.判断信息为偏好序的群决策方案排序:互补判断矩阵法[J].北京理工大学学报,2009,29(1):80- 83. [18] 侯福均,吴祈宗.Eigenvector mMethod for ranking alternatives with vague value measurements[J].北京理工大学学报(英文版),2009,18(2): 247-252. [19] 高峰记,张培龙,马浩静,雷红. 基于区间数的运输问题[C].西安:西部开发与系统工程——中国系统工程学会第12届年会论文集,2002:596- 600. Research on Solving Method of Vague Assignment Problem CUI Chun-sheng1,2 (1.CollegeofComputer&InformationEngineering,HenanUniversityofEconomicsandLaw,Zhengzhou450002,China; 2.InstituteofQuantitative&TechnicalEconomics,ChineseAcademyofSocialSciences,Beijing100010,China) The particularity of vague assignment problem is effective matrix expressed by vague values, which reflects the uncertainty and ambiguity of assignment problem. On the characteristics of vague value, vague assignment problem should be transformed into classlcs asslgnment problem. Thereof, with the “Matthew effect” function, the eigenvalues vector and Pareto, vague assignment problem can be solved. Finally, a group of data which comes from reference are calculated. Meanwhile, we get a desired result. operations research; vague assignment problem; score function; eigenvalue; pareto 2013- 09- 06 国家社科基金资助项目(12BTQ011);河南省高等学校青年骨干教师资助计划联合资助 崔春生(1974-),男,河南南阳人,副教授,博士后,研究方向:电子商务智能推荐,决策理论与方法。 O224 A 1007-3221(2015)02- 0058- 06



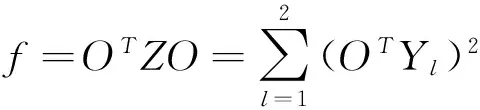

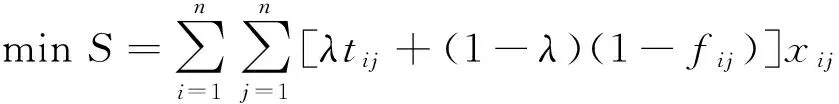

3 案例计算


4 结论

