也谈学生数学学习过程中的反思

张利春

【摘要】 培养学生把解题后的反思应用到整个数学学习过程中，养成检验、反思的习惯，是提高学习效果、培养能力的行之有效的方法. 学会在探究中反思，在交流中反思，在纠错中反思.

【关键词】 数学学习；反思

不会反思的老师不会是好老师，不会反思的学生不会是好学生，君子博学而日参省乎己，则知明而行无过矣，在数学学习过程中的反思是对自己形成的数学思想、方法和知识从另 一角度，以另一方式进行再认识以求得新的深入认识. 学生在数学学习过程中，只有不断地反思，才能够使自己所学的知识不断得到升华. 反思是对数学学习活动中所涉及的知识、方法、思路、策略等进行深入的研究，做到对所学的知识融会贯通、活学活用，不断提高学生的学习效率.

培养学生把解题后的反思应用到整个数学学习过程中，养成检验、反思的习惯，是提高学习效果、培养能力的行之有效的方法. 学会在探究中反思，在交流中反思，在纠错中反思. 一、知识点关联反思

反思知识的形成过程，揭示问题的本质，探索一般规律，是掌握概念、公式、定理的重要环节. 因为各种概念、公式、定理是学生学习的主要知识点，而课本对这些知识多数都是现成的理论，靠死记硬背是很难牢固掌握的. 因此，学生在学习数学时，应运用已有的知识、经验、方法对所学内容进行反思，多问几个为什么，通过反思去探索知识的形成过程，这样既让学生了解问题的本质，揭示一般规律，又加深了学生对知识的理解和记忆. 例如：学习角平分线性质和线段的垂直平分线性质，反思两个性质中提到的距离有什么区别，可以加深对性质的理解.

二、学习方式的反思

主要记录学生在数学学习过程中与同学互相学习、合作交流的情况. 例如：记录一节课帮助同学的次数，得到同学帮助的次数，自己有哪些收获感悟，有没有意外的灵感，有没有峰回路转的欣喜. 反思知识的形成过程，揭示问题的本质，探索一般规律，是掌握概念、公式、定理的重要环节. 因為各种概念、公式、定理是学生学习的主要知识点，而课本对这些知识多数都是现成的理论，靠死记硬背是很难牢固掌握. 因此，学生在学习数学时，应运用已有的知识、经验、方法对所学内容进行反思，多问几个为什么，通过反思去探索知识的形成过程，这样既让学生了解问题的本质，揭示一般规律，又加深了学生对知识的理解和记忆.

三、考试后的自我反思

主要反思学生在数学考试前的应试情况，考试中的做题情况和考试后的经验总结情况. 例如：反思考试成功在哪里，失败在哪里，哪些失误是因为粗心造成的，哪些失误是由于对知识点掌握不准确造成的，哪些失误是由于没有学会方法造成的，最好用笔反思到卷面上，然后进行纠错，这样做对知识的深化和巩固效果会更好.

四、解题反思

初中学生的数学反思能力的培养不仅要靠教师的正确指导，更需要学生自身的积极主动的学习. 教师在各个教学环节中要注重强化学生的反思意识，指导反思的技巧，培养学生形成良好的反思习惯和善于探索的数学学习思维. 正处于思维发展阶段的中学生，不可能一次性直接地把握学习活动的本质. 那么对于解题究竟反思些什么呢？

1. 反思结果的正确性

通过对结果的反思，能发现和纠正运算中失误之处，或对解题合理性进行检验，找到症结所在，然后作出适当的补充和调整. 例如，在解方程时，最后结果是否正确，是否为原方程的解，可以代入原方程进行检验. 当发现不满足原方程时，促使学生反思哪一步出现了错误，找到失误所在，作出修改，避免以后再犯类似错误.

2. 反思解答是否全面

学生在解题时易犯考虑不周、以偏概全或漏解的错误，在教学时要引导学生反思解答是否全面、完整. 例如，直角三角形两边长为3，4，求其第三边长. 学生往往误以为第三边是斜边，草率写出答案，所以学生得出了答案，并不意味着解题的结束，教师应因势利导，辨析题意，尤其针对一题两解，一题多解，深入剖析，及时纠正学生思考问题的片面性.

3. 反思解题思路

审题是对问题所给已知条件逐一思考，把它们可能出现的结果进行筛选、综合，并挖掘隐含条件，然后确定正确简捷的解题思路. 例如：“直角三角形的三条边长为三个连续整数，求它的面积. ”很多学生都想到了用方程解决，于是，设了未知数，三条边也分别用未知数表示出来，可有的学生苦于找不到相等关系，陷入了困境. 此时，教师应及时引导学生：“直角三角形的三边有什么关系？”学生经老师提醒后，很快就想起了“勾股定理”. 当学生思路陷入困境时，教师要及时引导学生反思：是否注意到了题目中的隐含条件，是否深入到问题的本质？经过这样反思，可以促使学生的思维朝着精细、深入的方向发展.

4. 反思题目的引申、推广

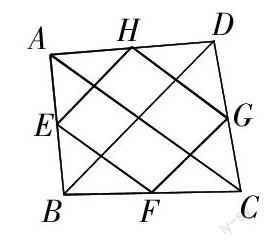
不失时机地引导学生将某些题目适当引申、推广，可以激发学生的求知欲，培养学生自觉探究的习惯，起到举一反三、事半功倍的作用. 例如：已知，如图，在四边形ABCD中，AC = BD，E，F，G，H分别是边AB，BC，CD，DA的中点. 求证：四边形EFGH是菱形.（证明略）变式：在菱形ABCD中，E，F，G，H分别是边AB，BC，CD，DA的中点. 证明：四边形EFGH是矩形.

总之，在解题过程中，要有意引导学生进行反思，充分暴露学生思维过程，养成自我发现、自主探索解题思路和方法的习惯，从而提高学生分析问题解决问题的能力. 不仅如此，教师还要注重培养学生自我反思的能力，使得反思更加有效. 教学实践表明：在数学学习中，反思是发现的源泉，不仅可以提高学生的数学意识，优化学生的思维品质，也可以沟通新旧知识间的联系，提高学习能力，提升学习素养，从反思中找到方法，找到快乐. C