追寻“简单熟练”背后的“深刻与丰富”

娄森锋

笔者对比了人教版实验教材（简称R）、浙教版教材（简称Z）、苏教版教材（简称S）对于“除数是两位数除法”教学过程，从计算方法的自动化，计算方法的多样化，计算方法的模型化上进行了差异比较.

（一）计算方法的自动化

“计算方法的自动化”：我们界定为学生在计算时，计算方法作为一种程序性的技能，学生在头脑中能即时提取程序进行计算. 用以评定学生的计算方法掌握情况和计算方法的抗干扰性.

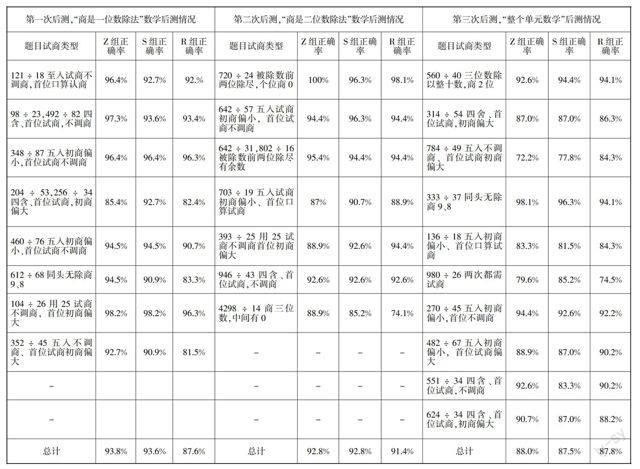
1. R、Z、S组对象计算正确率后测统计

2. 分析思考与建议

分析：

（1）从第一次后测来看，Z组正确率高于S组和R组，8个小题的正确率都高于另外两组，其中有两题高出R组十几个百分点，这是始料未及的. 分析原因是Z组首位试商的方法学生更容易找到初商，同时按照教材安排Z组和S组进行了试商技巧同头无除商9、8的教学，R组没有；另R组四舍五入试商和调商教学是一课时的.

（2）第二次后测来看Z组703 ÷ 19类型的正确率低于S组和R组，分析原因是首位试商对于除数是十几类型不适合，要采用口算来试商，提高了难度. 4298 ÷ 14商三位数，中间有0的除法正确率，Z组、S组高于R组，分析原因是Z组、S组教学时练习中出现，R组没有.

（3）第三次后测来看，Z组、S组和R组正确率接近. 分析原因是R组进行一些练习和训练，Z组、S组按照课时授课完成教材练习，配套练习采用R组作业本. 980 ÷ 26类型两次都需试商的计算，三组对象的正确率都偏低. 分析原因是商两位教学Z组、R组一课时，S组只在练习中出现.

建议：

（1）R组教学中四舍五入试商和调商教学分课时进行，以降低难度；可适当增加试商技巧的教学.

（2）R组教学应增加口算练习的安排；Z组教学时首位试商法和四舍五入估算容易发生冲突，因此对496 ÷ 77 ≈ 类型的估算答案应开放；三组对象都应加强估算的教学.

（3）Z组、S组和R组980 ÷ 26类型两次都需试商的计算需成课教学，同时渗透商三位数，中间有0的除法的练习，为小数除法孕伏.

（二）计算方法的多样化

1. 多种方法计算后测情况统计.

第一次教学后，用125 ÷ 25这道题进行了测试：Z、S、R组一种方法分别占16.4%、49.1%、50%. 两种方法分别占69.1%、45.5%、22.2%. 三种方法分别占1.8%、1.8%、0%.

第二次教学后，用800 ÷ 25这道题进行了测试：Z、S、R组一种方法分别占7.4%、5.6%、22.2%. 两种方法分别占14.8%、27.8%、61.1%. 三种方法分别占51.9%、46.3%、11.1%. 四种方法分别占24.1%、18.5%、0%. 还用533000 ÷ 2600这道题进行了测试：Z、S、R组正确率分别是64.8%、61.1%、42.6%.

第三次单元教学后，用9000 ÷ 125和360 ÷ 24这两道题进行了测试：Z、S、R组一种方法分别占2.7%、10.9%、25.6%. 两种方法分别占35.5%、34.5%、59.1%. 三种方法分别占45.5%、37.3%、0.9%. 四种方法分别占4.5%、6.4%、0%. 还用8700 ÷ 290和73200 ÷ 2400这两道题进行了测试：Z、S、R组正确率分别是79.6%、84.3%、84.3%.

第一次后测时，没有进行商不变性质的学习，后两次测试都在商不变性质学习后进行.

2. 分析思考与建议

分析：

（1）从三次后测情况来看，Z组在计算方法的多样性上好于S组、R组，R组在计算方法的多样性上更低. 分析原因是Z组不仅安排了选做题280 ÷ 35 = 280 ÷ （7 × 5） = 280 ÷ 7 ÷ 5的练习，还专门安排了商不变性质的运用课，呈螺旋上升序列安排，R组只在配套作业本上出现，S组商不变性质不在这个单元教学.

（2）从三次后测情况来看，S组在计算方法的多样性上接近Z组. 分析原因是S组商不变性质不在这个单元教学，为了完成教学任务采用了Z组教学安排进行了学习，同时还因为Z组、S组的授课教师是同一人，在练习课教学中进行了补救. R组在新授时和练习时都忽略了计算方法多样的讨论，第一次后测发现问题后进行补救不到位，相当一部分学生认为列竖式计算这个基本方法不算多种方法之一.

建议：

（1）S组、R组教材应增加计算方法多样化练习，增加运用商不变的性质进行简便计算一课时，从而实现学生在计算方法上的完整性和灵活性.

（2）有意识的增加计算方法多样化练习频次，让学生有更多的机会运用多种方法进行计算，提升学生灵活计算的意识和能力.

（三）计算方法的模型化

所谓计算方法的模型化，我们认为是学生比较深刻的认识计算的过程和方法，能够体悟除数是两位数除法计算的算法模型，借助于抽象符号概括算法，发展抽象思维.

1. 计算方法的模型化后测情况统计

分析思考与建议：

分析：

（1）从第一次后测来看，Z组、S组学生计算方法的深刻性远超R组学生. 分析原因是Z组、S组在进行口算教学时，有学生提出“被除数和除数同时划0”的方法口算，学生留下的印象比较深刻.

（2）从第二次后测来看，三组学生均能很好的理解CDCDCD ÷ CD = 10101這个模型， Z组偏低是因为有2个待评的学生，影响了正确率. 分析原因是这个模型比较直观，三组学生都补充了商中间有0的除法教学.

（3）从第三次后测来看，三组学生计算方法的模型化仍然没有很好的建立. 分析原因是三组学生都没有进行这方面的练习.

建议：

（1）学生能够直观地体悟除数是两位数除法计算的算法模型，应该有意识地帮助学生建立；三组教材应补充商中间有0的除法教学；

（2）Z组、S组和R组教材都应在教学时渗透算法模型化的练习，提升学生对计算方法掌握的深刻性.