基于高斯混合带势概率假设密度滤波器的未知杂波下多机动目标跟踪算法
胡子军张林让张 鹏王 纯
①(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)
②(西安建筑科技大学信息与控制工程学院 西安 710055)
基于高斯混合带势概率假设密度滤波器的未知杂波下多机动目标跟踪算法
胡子军*①张林让①张 鹏①王 纯②
①(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)
②(西安建筑科技大学信息与控制工程学院 西安 710055)
多模型的随机有限集(RFS)类方法是一类有效的多机动目标跟踪算法,但是现有算法都假定杂波统计特性先验已知,不适用于未知杂波背景。该文以高斯混合带势概率假设密度滤波器(GMCPHDF)为基础,提出一种未知杂波下的多机动目标跟踪算法。该算法对目标和杂波分别独立建模,通过最优高斯(BFG)估计方法对真实目标的强度函数进行预测,从而使多目标强度函数独立于机动目标的运动模型,实现各时刻真实目标的强度函数、杂波源期望个数以及真实目标和杂波源的混合势分布的迭代。仿真结果表明,该算法能够有效地联合估计多机动目标状态以及杂波期望个数。
多机动目标跟踪;未知杂波;带势概率假设密度滤波器;最优高斯估计
1 引言
现代航空学的快速发展,特别是各种战斗机和无人飞行器的高机动性,使得多机动目标跟踪问题成为当前迫切需要解决的课题。基于随机有限集(Random Finite Set, RFS)理论的多目标贝叶斯估计方法是近年来快速发展的多目标跟踪方法[1- 5],相比于传统的关联算法,该类算法用随机有限集表征各时刻多个目标的状态和观测信息,使得该类算法避开了高复杂的关联问题。基于此优势,大量学者尝试将典型的随机有限集方法扩展到多模型,以解决多个机动目标的跟踪问题[6- 10]。但是所有这些算法都假定场景中杂波是静态的,且服从一先验已知的泊松分布。而实际的电子战环境中,杂波环境是动态未知的,当多目标跟踪算法中的杂波模型与真实的杂波统计特性失配时,会导致目标不能被有效跟踪以及大量的虚假航迹出现。
文献[11-13]尝试基于RFS方法跟踪未知杂波背景下的多目标。文献[11]扩展概率假设密度滤波器(Probability Hypothesis Density Filter, PHDF),跟踪非齐次慢时变杂波背景下的多目标;文献[12,13]假定场景中有多个杂波源,各杂波源独立地以一定的检测概率产生杂波观测值,分别基于带势概率假设密度滤波器(Cardinalized PHDF, CPHDF)和势平衡多目标多重伯努利(Cardinality Balanced Multi-target Multi-Bernoulli, CBMeMBer)滤波器对杂波和目标同时估计。但是这些算法都没有考虑到目标的机动,当目标机动时,目标的强度函数是受到目标的运动模型约束的多模型形式,但是杂波源的状态转移函数是单模型的,这样真实目标和杂波源的混合状态就无法统一迭代。
本文基于未知杂波下的高斯混合(Gaussian Mixture, GM)CPHDF,一方面采用杂波源以一定的检测概率产生杂波的方法对杂波建模,另一方面利用最优高斯(Best-Fitting Gaussian, BFG)估计方法预测真实目标的强度函数,使得真实目标的多模型强度函数由一单模型的强度函数等效,从而实现未知杂波背景下多机动目标状态和杂波期望个数的联合估计。
2 未知杂波下的GMCPHDF
类似于真实目标,对杂波建模如下:假定场景中有多个独立同分布的杂波源,各杂波源独立地新生和消亡,且以确定的杂波检测概率产生杂波观测值。以分别表征k时刻真实目标状态有限集和杂波源状态有限集,则k时刻目标和杂波源的混合状态有限集为且杂波源和真实目标不能相互转换;同样k时刻混合观测有限集为分别表征真实目标观测集和杂波观测集。在混合状态集和混合观测集下利用CPHDF,滤波器的迭代变量扩展为真实目标的强度函数,杂波源的强度函数以及真实目标和杂波源的混合势分布。就杂波而言,系统仅关心其在各时刻的观测值期望个数,同时独立同分布的杂波源的强度函数完全由杂波源期望个数决定。因此未知杂波下的CPHDF联合迭代真实目标的强度函数,杂波源的期望个数以及真实目标和杂波源的混合势分布pk(·)。

,k;(6)真实目标和杂波源的新生混合势分布为pΓ,k(·),混合势分布的最大可能个数为Nmax。未知杂波下的GMCPHDF迭代过程包括预测和更新两步[11]。
则对应的k时刻的预测变量分别为
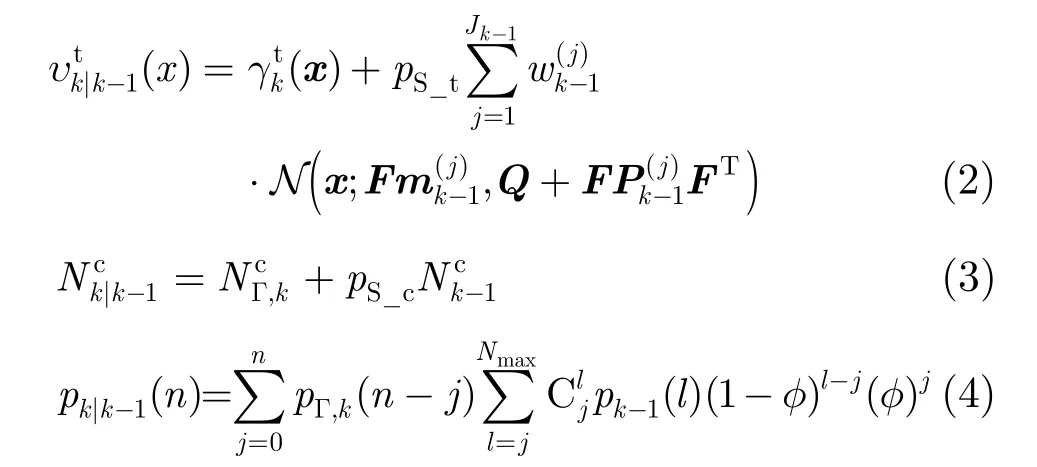


尽管标准的未知杂波下的GMCPHDF提供了一种有效的未知杂波背景下的多目标跟踪算法,但是其迭代公式的推导是以真实目标的运动模型是单模型为前提的,而机动目标的运动模型通常用线性高斯跳变的多模型系统表征,因而该算法不能直接用于未知杂波背景下的多机动目标跟踪。下节先利用BFG估计方法,用一等效的线性高斯单模型系统预测机动目标的强度函数,然后利用未知杂波背景下的GMCPHDF的更新公式估计多机动目标的后验强度函数、杂波的后验期望个数以及目标和杂波源的后验混合势分布,从而实现未知杂波背景下多机动目标状态和杂波期望个数的联合估计。
3 未知杂波背景下的多机动目标跟踪算法
3.1 线性高斯跳变系统下的BFG估计
多模型(Multiple-Model, MM)算法是机动目标跟踪的经典算法[14],由于机动目标在各时刻的运动模型不确定,MM算法假定目标的运动模型集合已知,各模型间的相互转换概率由马尔科夫矩阵Tp=[tq, r]表征,其中tq, r≜Pr(rk=r| rk-1=q ),通过迭代各时刻目标的模型概率、目标状态在各模型下的条件均值和条件协方差矩阵,实现对机动目标的跟踪。本文仅针对线性高斯的目标运动模型,线性高斯下的机动目标运动模型可由一线性高斯跳变系统表征

假定k-1时刻的目标状态均值εk-1,协方差矩阵Θk-1,模型概率πk -1(r)≜Pr(rk -1=r ),则由全概率公式,k时刻的预测模型概率πk| k-1(r )、均值和协方差矩阵分别为

文献[15]提出一种BFG估计方法,在机动目标的运动模型为线性高斯跳变系统的前提下,用一线性高斯单模型系统:

等效机动目标的多模型系统。其基本思想是确保等效后的单模型系统预测的目标状态的一阶、二阶统计特性和等效前的MM方法预测的相同。对于BFG估计的单模型系统,其预测均值εk| k-1,预测协方差矩阵Θk| k-1分别为基于BFG估计的等效准则,令由式(10)、式(11)、式(13)和式(14),得到线性高斯单模型系统的状态转移矩阵Φk-1和状态噪声协方差矩阵Σk-1的计算公式。

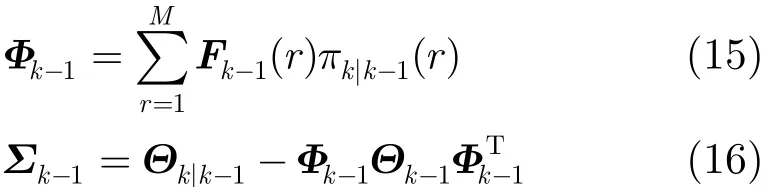
由于线性高斯模型下的贝叶斯估计算法仅考虑目标状态的一阶、二阶统计特性,而BFG估计方法确保等效前后预测的目标状态的一阶、二阶统计特性不变,因而相对于MM方法,其性能没有损失。
3.2 基于GMCPHDF的多机动目标和杂波的联合估计
本节利用BFG估计,将机动目标的线性高斯跳变系统转化为单模型系统,进而利用未知杂波下的GMCPHDF框架对多机动目标状态以及杂波期望个数联合估计。相对于文献[11]中的标准的未知杂波背景下的GMCPHDF,不同之处主要在预测步骤,更新步骤基本一致。
步骤 1 利用BFG估计方法预测真实目标强度函数的存活高斯分量 具体分以下几个子步骤:
(4)高斯分量的协方差矩阵预测:

步骤 2 合并真实目标强度函数的新生高斯分量和存活高斯分量

步骤 3 杂波源的期望个数预测 应用式(3)。
步骤 4 真实目标和杂波源的混合势预测BFG估计使得真实目标势分布独立于运动模型,因而可以应用非机动目标跟踪算法的混合势预测公式,公式(4)。
步骤 5 更新 利用k时刻的观测集Zk,应用式(5),式(6)和式(7)。
步骤 6 修剪合并高斯分量 得到k时刻真实目标强度函数的高斯分量集杂波源的后验期望个数以及真实目标和杂波源的混合势分布
步骤 7 真实目标的状态提取以及杂波期望个数估计
4 实验结果
本节验证本文算法联合估计未知杂波下的多机动目标状态和杂波期望个数的有效性,并和两种已知杂波背景下的多机动目标跟踪算法比较:分别采用文献[9]的多模型CPHDF和基于BFG估计的GMCPHDF,考察杂波统计特性未知导致跟踪性能的损失情况。

其中Ω为角速度,采样步长T=1.0 s , σv为运动噪声标准差。3个模型间状态转移矩阵为:Tp=传感器仅观测位置信息,观测矩阵和观测噪声协方差矩阵分别为I为2维单位矩阵。
2真实目标的存活概率,新生强度其中新生目标的先验模型概率矢量为τ=
γ,k[0.8,0.1,0.1]T。真实目标的检测概率p=0.98。仿
D_t真实验中杂波由个杂波源以检测概率的二项分布产生,杂波位置按照均匀分布在场景中随机生成。但是在跟踪过程中,这些信息是未知的。跟踪算法假定各时刻新生杂波源的个数=3,杂波源的存活概率杂波源的检测概率
在2维监视区域 [30, 42] km×[-50, -40] km中,5个机动目标先后在不确定时刻出现,运行轨迹如图1所示。目标1在第1个步长以(25,100) m/s的速度起始于(40,-50) km ,在第26个步长以π/60 rad/s的角速度做逆时针转弯,持续35个步长后转为匀速运动,直到第100个步长结束;目标2在第5个步长以(120,30) m/s的速度起始于(30,-42) km,在第16个步长以-π/60rad/s的角速度做顺时针转弯,35个步长之后再做匀速运动直到第85个步长结束;目标3在第10个步长以(5,-90) m/s 的速度起始于(40,-41) km,在第21个步长以-π/60 rad/s的角速度做顺时针转弯,30个步长之后转为匀速运动,持续20个步长之后再以π/60rad/s的角速度做逆时针转弯,直到第100个步长结束;目标4在第15个步长以(105,20) m/s的速度起始于(33,-48) km,在第56个步长转为以角速度为-π/60 rad/s的逆时针转弯,15个步长之后再转为匀速运动,直到第90个步长结束;目标5在第20个步长以(-55,70) m/s 的速度起始于(39,-48) km,一直到第95个步长结束。

图1 目标真实航迹和单次仿真的观测数据、航迹滤波值
单次仿真的航迹滤波结果以及观测数据见图1,尽管目标航迹间有交叉,且有大量虚假观测值,各时刻目标的估计位置仍能基本覆盖在真实航迹点上,这说明本文算法可以在未知杂波背景下跟踪上多个机动目标。
为了进一步评估本文算法的跟踪性能,并与两种已知杂波下的跟踪算法比较,保持航迹数据不变,蒙特卡罗仿真1000次,每次仿真的观测数据独立产生。得到的杂波期望个数估计曲线如图2所示,可以看出杂波的期望个数估计有约0.3的偏差,杂波期望个数均方根误差在0.7左右,这说明本文算法在稳定跟踪多个机动目标的同时,也能较准确地估计出各时刻环境中的杂波期望个数。目标个数的蒙特卡罗均值随时间变化的曲线如图3所示,可以看出,已知杂波背景下的多模型CPHDF(杂波已知(MM))和基于BFG的CPHDF(杂波已知(BFG))对目标个数的估计偏差在0.01的数量级上,针对未知杂波背景的本文算法对目标个数的估计偏离真实值约0.18。对应的目标个数均方根误差曲线如图4所示,可以看出,已知杂波背景下的两种算法的目标个数均方根误差比较接近,未知杂波背景下的目标个数均方根误差比已知杂波背景下的两种算法都要大,但三者在同一数量级。基于BFG的CPHDF在已知杂波背景下的目标个数均方根误差在时间段(85 ~100 s)内有较大波动,这是由于该时间段内依次有目标消亡,滤波器需要时间响应目标个数的变化。表征多目标跟踪误差的优化子模式分配 (Optimal SubPattern Assignment, OSPA)距离[17]如图5所示,可以看出未知杂波和已知杂波背景下的误差曲线变化趋势在整体上是一致的,但是在目标个数固定的时间段(25~85 s)内,未知杂波背景下的误差要比已知杂波背景下的两种算法的误差略大。这些数据说明:已知杂波背景下,基于BFG的CPHDF相对于文献[9]的多模型CPHDF的性能基本上没有损失。相比于已知杂波背景下的跟踪算法,尽管由于在未知杂波背景下所能利用的环境信息要少,使得本文算法的跟踪性能有一定程度的损失,但是仍能够较准确的联合估计多机动目标状态和杂波期望个数。
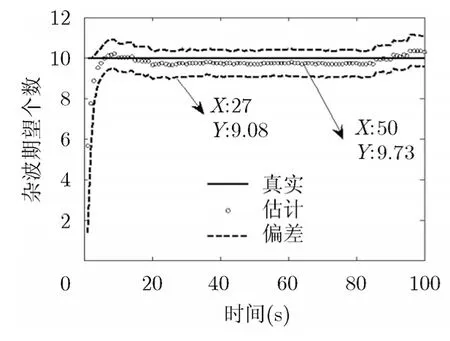
图 2 杂波期望个数估计

图 3 目标个数估计

图 4 目标个数均方根误差

图 5 OSPA距离(势误差参数c=200,阶数p=1)
5 结束语
针对未知杂波背景下多机动目标跟踪问题,提出了一种联合估计多机动目标状态和杂波期望个数的算法。该算法通过引入BFG估计方法将机动目标的多模型系统等效为单模型系统,从而利用非机动目标下的未知杂波GMCPHDF框架实现多机动目标跟踪。相比于已知杂波背景的多机动目标跟踪算法,跟踪性能有一定程度的损失,但是仍能够相对准确地跟踪上多个机动目标。如何更好的对杂波建模,进一步提高跟踪性能是今后需要开展的工作。
[1] Mahler R. Statistical Multisource-Multitarget Information Fusion[M]. Norwood, MA: Artech House, 2007: 305-682.
[2] Lundgren M, Svensson L, and Hammarstrand L. A CPHD filter for tracking with spawning models[J]. IEEE Journal of Selected Topics in Signal Processing, 2013, 7(3): 496-507.
[3] 扬威, 付耀文, 龙建乾, 等. 基于有限集统计学理论的目标跟踪技术研究综述[J]. 电子学报, 2012, 40(7): 1440-1448. Yang Wei, Fu Yao-wen, Long Jian-qian, et al.. The FISST-based target tracking techniques: a survey[J]. Acta Electronica Sinica, 2012, 40(7): 1440-1448.
[4] 谭顺成, 王国宏, 王娜, 等. 基于概率假设密度和数据关联的脉冲多普勒雷达多目标跟踪算法[J]. 电子与信息学报, 2013, 35(11): 2700-2706. Tan Shun-cheng, Wang Guo-hong, Wang Na, et al.. A probability hypothesis density filter and data association based algorithm for multitarget tracking with pulse Doppler radar[J]. Journal of Electronics & Information Technology, 2013, 35(11): 2700-2706.
[5] 杨可, 傅中谦, 王剑亭, 等. 多目标滤波中的多传感器概率假设密度算法[J]. 电子与信息学报, 2012, 34(6): 1369-1373. Yang Ke, Fu Zhong-qian, Wang Jian-ting, et al.. Multi-sensor probability hypothesis density algorithm in multi-target filtering[J]. Journal of Electronics & Information Technology, 2012, 34(6): 1369-1373.
[6] Punithakumar K, Kirubarajan T, and Sinha A. Multiple-model probability hypothesis density filter for tracking maneuvering targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(1): 87-98.
[7] Ouyang Cheng, Ji Hong-bing, and Guo Zhi-qiang. Extensions of the SMC-PHD filters for jump Markov systems[J]. Signal Processing, 2012, 92 (6): 1422-1430.
[8] Pasha S A, Vo B N, Tuan H D, et al.. A Gaussian mixture PHD filter for jump Markov system models[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(3): 919-936.
[9] Georgescu R and Willett P. The multiple model CPHD tracker[J]. IEEE Transactions on Signal Processing, 2012, 60(4): 1741-1751.
[10] Yang Jin-long, Ji Hong-bing, and Ge Hong-wei. Multi-model particle cardinality-balanced multi-target multi-Bernoulli algorithm for multiple manoeuvring target tracking[J]. IET Radar, Sonar & Navigation, 2013, 7(2): 101-112.
[11] Mahler R, Vo B T, and Vo B N. CPHD filtering with unknown clutter rate and detection profile[J]. IEEE Transactions on Signal Processing, 2011, 59(8): 3497-3513.
[12] Chen X, Tharmarasa R, Pelletier M , et al.. Integrated clutter estimation and target tracking using Poisson point process[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(2): 1210-1235.
[13] Vo B T, Vo B N, Hoseinnezhad R, et al.. Robust multi-Bernoulli filtering[J]. IEEE Journal of Selected Topics in Signal Processing, 2013, 7(3): 399-409.
[14] Li X R and Jikov V P. Survey of maneuvering target tracking. part V: multiple-model methods[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4): 1255-1321.
[15] Hernandez M, Ristic B, Farina A, et al.. Performance measure for Markovian switching systems using best-fitting Gaussian distributions[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(2): 724-747.
[16] Vo B T, Vo B N, and Antonio C. Analytic implementations of the cardinalized probability hypothesis density filter[J]. IEEE Transactions on Signal Processing, 2007, 55(7): 3553-3567.
[17] Schuhmacher D, Vo B T, and Vo B N. A consistent metric for performance evaluation of multi-object filters[J]. IEEE Transactions on Signal Processing, 2008, 56(8): 3447-3457.
胡子军: 男,1982年生,博士生,研究方向为多目标跟踪.
张林让: 男,1966年生,教授,博士生导师,研究方向为自适应信号处理、阵列信号处理、非平稳信号处理、雷达系统建模、仿真与评估.
张 鹏: 男,1974年生,博士生,研究方向为雷达弱小目标的检测和跟踪.
Gaussian Mixture Cardinalized Probability Hypothesis Density Filter for Multiple Maneuvering Target Tracking under Unknown Clutter Situation
Hu Zi-jun①Zhang Lin-rang①Zhang Peng①Wang Chun②①(National Laboratory of Radar Signal Processing, Xidian University, Xi’an 710071, China)
②(College of Information and Control Engineering, Xi’an University of Architecture and Technology, Xi’an 710055, China)
Considering the limitation of the well-known multiple model formulation of the Random Finite Set (RFS) that the statistics characteristic of clutter is assumed to be known a priori, this paper proposes a new multiple maneuvering target tracking algorithm based on Gaussian Mixture Cardinalized Probability Hypothesis Density Filter (GMCPHDF) in the case of unknown clutter. The proposed method predicts the intensity function of actual target states by Best-Fitting Gaussian (BFG) approximation, which is independent of the target motion model. Then the closed-loop iteration procedure among the intensity function of actual target states, the mean number of clutter generators, and the hybrid cardinality distribution of actual targets and clutter generators is established. The simulation results show that the proposed method can effectively estimate the target number, target states and the mean number of clutters simultaneously.
Multiple maneuvering target tracking; Unknown clutter; Cardinalized Probability Hypothesis Density Filter (CPHDF); Best-Fitting Gaussian (BFG) approximation
TP391
A
1009-5896(2015)01-0116-07
10.11999/JEIT140218
2014-02-19收到,2014-06-19改回
国家自然科学基金(61301281)资助课题
*通信作者:胡子军 huzijun007@126.com

