AM-凸函数及其Jensen型不等式

宋振云

（湖北职业技术学院 机电工程学院，湖北 孝感 432000）

0 引言

在数学规划、控制论、最优化等非线性分析领域，凸性及其广义凸性所发挥的不可替代作用［1-3］已众所周知.随着其研究的深入，应用的广泛性被不断向外拓展，应用的价值也愈来愈明显.近年来，凸性及其广义凸性受到众多专家学者的关注，使得对凸性和广义凸性的研究成为热点，尤其是关于凸性和广义凸性的各类新的凸函数概念被不断提出，进而被进一步深入研究和广为应用，仅就实数区间上的二元幂平均所给出的凸函数，就有如几何凸函数［4］、调和凸函数［5］、平方凸函数［6］、对数凸函数［7］、AH-凸函数［8］、GA-凸函数［9］、GH-凸函数［10］、HA-凸函数［11］、HG-凸函数［12］等，又如rP-凸函数［13］、P-凸函数［14］、MG-凸函数［15］、GM-凸函数［16］等.

本文基于应用上对函数凸性的特殊要求，考虑对凸函数、对数凸函数、AH-凸函数的进一步推广问题，给出了AM-凸函数的定义，讨论了AM-凸函数的判定定理和相关性质，建立了AM-凸函数的Jensen型不等式.

定义1设I⊆(0,+∞)，f(x)是I上的正值函数，如果 ∀x1,x2∈I及 ∀t∈[0,1]，存在r∈R，使得

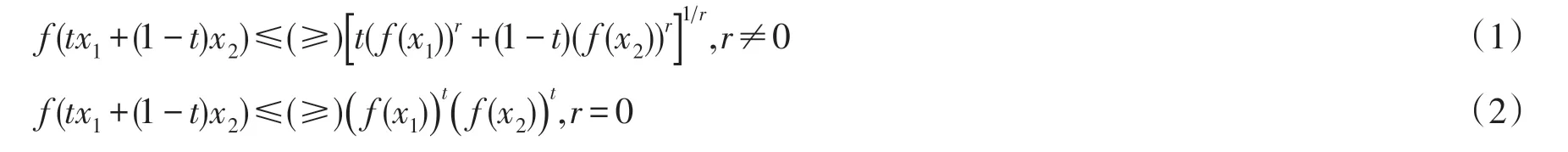
则称f(x)为I上的AM-凸（凹）函数.其中，当r＞0 时，称f(x)为I上的AMr+-凸（凹）函数，当r＜0 时，称f(x)为I上的AMr--凸（凹）函数.

注1当r=0 时，AM-凸（凹）函数即为对数凸（凹）函数，当r=1 时，AM-凸（凹）函数即为通常的凸（凹）函数，当r=-1时，AM-凸（凹）函数即为AH-凸（凹）函数.

1 关于AM-凸函数的判定

全文约定所有讨论只考虑r≠0 的情形，对r=0 时的相关讨论见文献［7］.

定理1设I⊆(0,+∞)，f(x)是I上的正值函数，则

（i）f(x)为I上的 AMr+-凸（凹）函数的充要条件是：∀x1,x2,x3∈I且x1＜x2＜x3，有

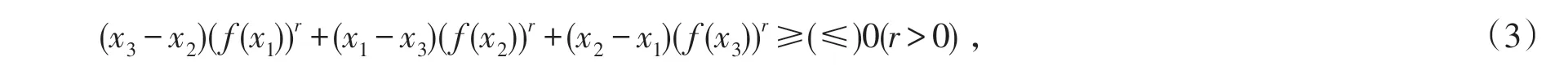
（ii）f(x)为I上的 AMr--凸（凹）函数的充要条件是：∀x1,x2,x3∈I且x1＜x2＜x3，有

证明只证（i），同理可证（ii）.

若f(x)为I上的AMr+-凸函数，则

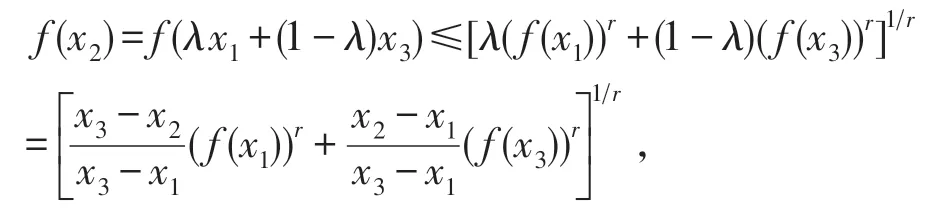
因为f(x)是I上的正值函数，r＞0，所以，将上式整理即得

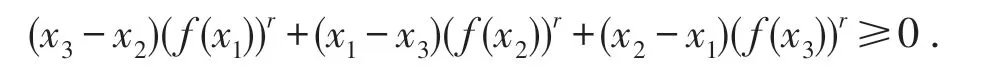
由于r＞0 时，以上证明步步可逆，所以充分性成立.若f(x)在I上是AMr+-凹的，则上述证明中的不等号反向，因此定理1（i）的后半部分成立.

定理2设I⊆(0,+∞)，f(x)是定义在I上的正值函数，则

（i）f(x)为I上的 AMr+—凸（凹）函数的充要条件是(f(x))r(r＞0)为I上的凸（凹）函数；

（ii）f(x)为I上的 AMr--凸（凹）函数的充要条件是(f(x))r(r＜0)为I上的凹（凸）函数.

证明只证（i），同理可证（ii）.

设g(x)=(f(x))r（x∈I且r＞0），如果g(x)=(f(x))r为I上的凸函数，注意到r＞0，那么 ∀x1,x2∈I及∀t∈[0,1]，则有

所以，f(x)为I上的AMr+-凸函数.

如果f(x)为I上的AMr+-凸函数，r＞0，那么 ∀x1,x2∈I及 ∀t∈[0,1]，则有

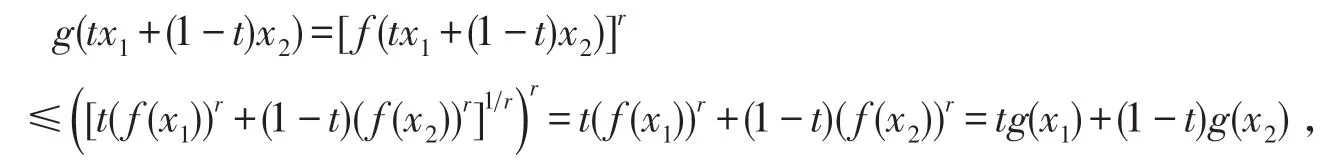
因此，g(x)=(f(x))r是I上的凸函数.

若f(x)在I上是AMr+-凹的，则上述证明中的不等号反向，所以定理2（i）的后半部分成立.

定理3设I⊆(0,+∞)，f(x)是定义在I上的正值函数，则

（i）f(x)为I上的 AMr+-凸（凹）函数的充要条件是φ(t)=[f(tx1+(1-t)x2)]r(x1,x2∈I且r＞0)为[0,1]上的凸（凹）函数；

（ii）f(x)为I上的 AMr--凸（凹）函数的充要条件是φ(t)=[f(tx1+(1-t)x2)]r(x1,x2∈I且r＜0)为[0,1]上的凹（凸）函数.

证明只证（i），同理可证（ii）.

充分性 因为φ(t)=[f(tx1+(1-t)x2)]r(t∈[0,1])，所以φ(0)=(f(x2))r，φ(1)=(f(x1))r，又φ(t)为 [0,1]上的凸函数，且r＞0，所以，

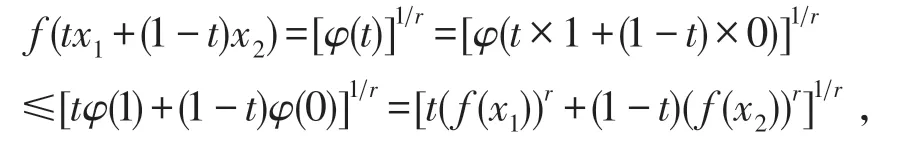
故函数f(x)为I上的AMr+-凸函数.

必要性 ∀x1,x2∈I及 ∀t1,t2∈[0,1]，有两个正数的幂平均的性质［17］，有

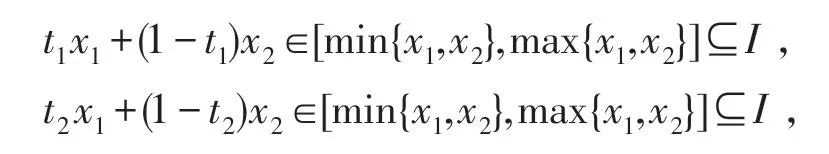
令X1=t1x1+(1-t1)x2，X2=t2x1+(1-t2)x2，则 ∀α∈[0,1]，亦有αX1+(1-α)X2∈I，若f(x)是I上的AMr+-凸函数，则 ∀t1,t2∈[0,1]，∀α∈[0,1]，并注意到r＞0 即有

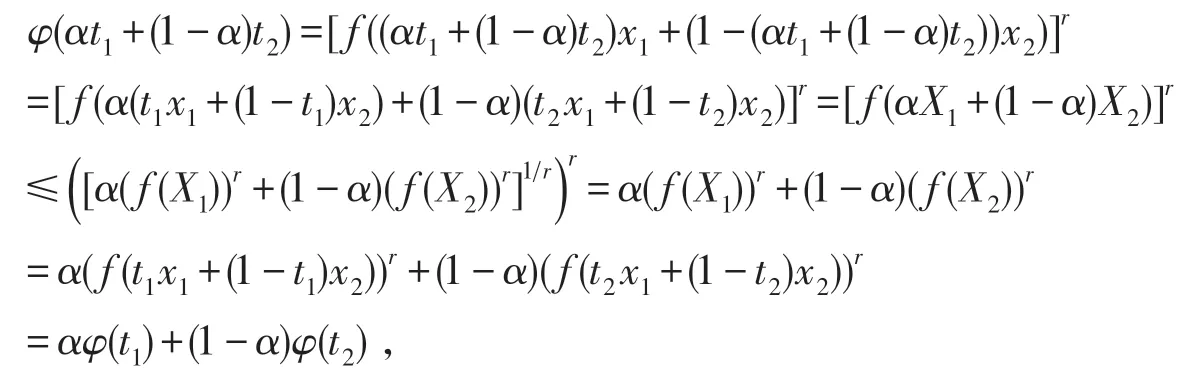
所以，函数φ(t)=(f(tx1+(1-t)x2))r(r＞0)是[0,1]上的凸函数.若f(x)在I上是AMr+-凹的，则上述证明中的不等号反向，因此定理3（i）的后半部分成立.

定理4设I⊆(0,+∞)，f(x)是定义在I上的正的二阶可导函数，则

（i）f(x)为I上的AMr+-凸（凹）函数的充要条件是：

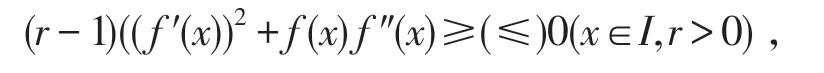
（ii）f(x)是I上的AMr--凸（凹）函数的充要条件为：

证明只证（i），同理可证（ii）.

求函数g(x)=(f(x))r在I上的一阶、二阶导数，得

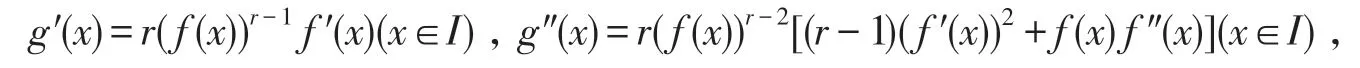
因为f(x)在I上是正的，所以，g″(x)≥(≤)0 ⇔r[(r-1)(f′(x))2+f(x)f″(x)]≥(≤)0(x∈I)，由定理2，f(x)为I上的AMr+-凸（凹）函数⇔g(x)=(f(x))r为I上的凸（凹）函数

定理5设I⊆(0,+∞)，f(x)是定义在I上的可导正值函数，且f′(x)连续，则

（i）f(x)为I上的 AMr+-凸（凹）函数的充要条件是：

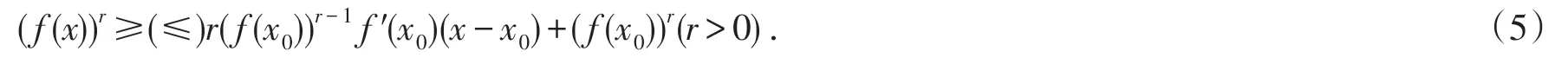
（ii）f(x)为I上的AMr--凸（凹）函数的充要条件是：

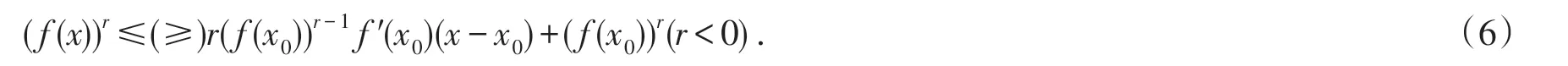
证明只证（i），同理可证（ii）.对AM-凸函数定义中的权变量t∈[0,1]，易证t=0,1 定理成立.下面证明t∈(0,1)时定理成立.

充分性 ∀x1,x2∈I，令x0=tx1+(1-t)x2(t∈(0,1))，则x0∈I，若不等式（5）成立，则

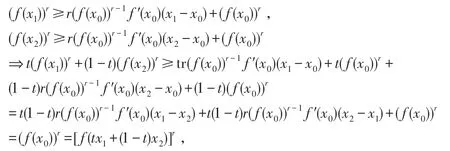
由于r＞0，所以，f(tx1+(1-t)x2)≤[t(f(x1))r+(1-t)(f(x2))r]1r.

故，f(x)为I上的AMr+-凸函数.

必要性 设f(x)为I上的AMr+-凸函数，r＞0，则 ∀x0,x∈I(x0≠x)，∀t∈(0,1)，有

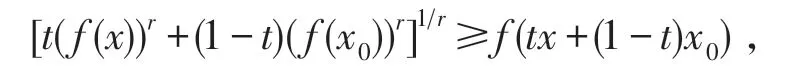
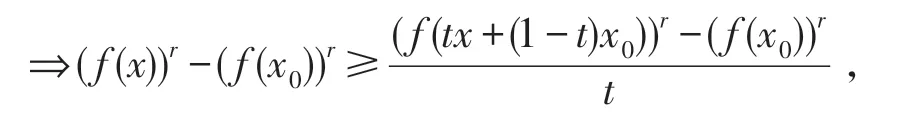
求t→0+的极限，并注意到f′(x)的连续性，则得

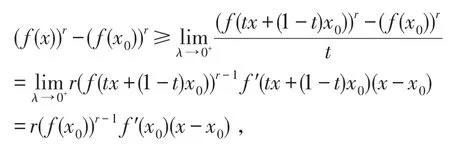
故

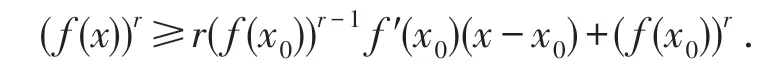
同理可证定理5（i）的后半部分成立.

2 关于AM-凸函数的性质

定理6设I⊆(0,+∞)，f(x)是定义在I上的正值函数，

（i）如果f(x)为I上严格递减的rP-凸函数，那么当 0＜r≤1 时，f(x)为I上的 AMr+- 凸函数；当r＜0时，f(x)为I上的AMr--凸函数；

（ii）如果f(x)为I上严格递增的rP-凸函数，那么当r≥1时，f(x)为I上的AMr+-凸函数；

（iii）如果f(x)为I上严格递增的rP-凹函数，那么当 0＜r≤1时，f(x)为I上的 AMr+-凹函数；当r＜0时，f(x)为I上的AMr--凹函数；

（iv）如果f(x)为I上严格递减的rP-凹函数，那么当r≥1时，f(x)为I上的AMr+-凹函数.

证明只证（i），同理可证（ii）（iii）（iv）.

当 0＜r≤1时，∀x1,x2∈I及 ∀t∈[0,1]，由幂平均的单调性知因为f(x)为I上严格递减的rP-凸函数，所以

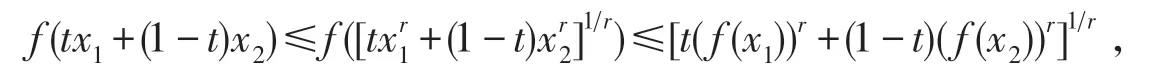
故f(x)为I上的AMr+-凸函数.

当r＜0 时，由于，且f(x)是I上严格递减的rP-凸函数，所以

因此，f(x)为I上的AMr--凸函数.

定理7设I⊆(0,+∞)，f(x)是定义在I上的正值函数，

（i）如果f(x)为I上的AMr--凸函数，那么是I上的 AMr+-凹函数；

（ii）如果f(x)为I上的AMr+-凹函数，那么是I上的AMr--凸函数.

证明只证（i），同理可证（ii）.

由Cauchy不等式［18］，∀x1,x2∈I及 ∀t∈[0,1]，有

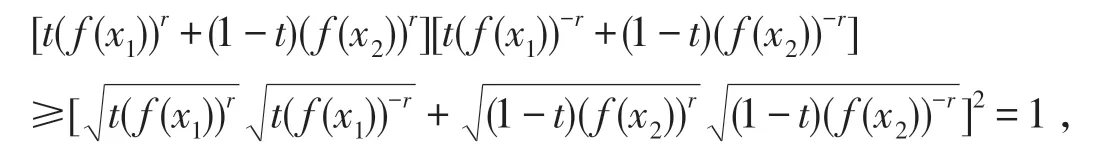
因为f(x)在I上是正的，所以，

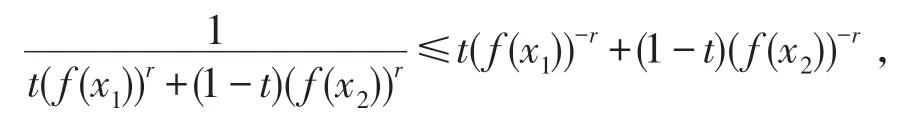
注意到r＜0，因此，

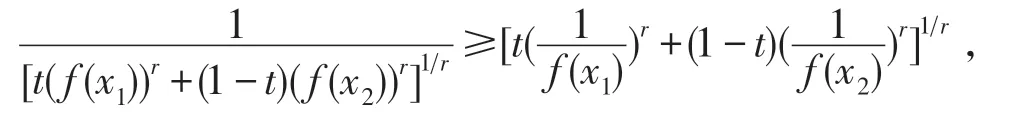
又f(x)是I上的AMr--凸函数，且f(x)＞0，所以，∀x1,x2∈I及∀t∈[0,1]，有

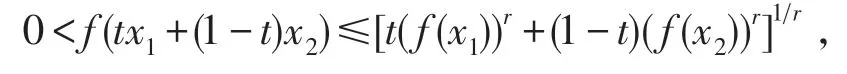
因而

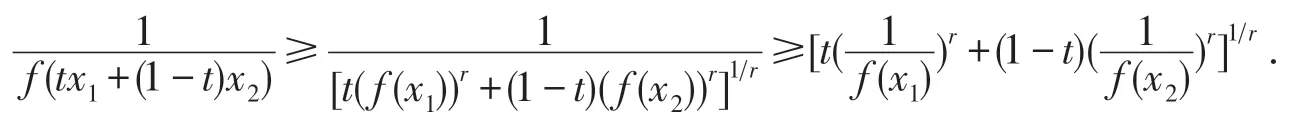
定理8设I,D⊆R+，f:I→D，且f(I)=D，那么

（i）若y=f(x)为I上严格递增的AM-凸函数，则当 0＜r≤1 时，其反函数y=f-1(x)为D上的 AMr+-凹函数；当r＜0 时，其反函数y=f-1(x)为D上的AMr--凹函数；

（ii）若y=f(x)为I上严格递增的AM-凹函数，则当r≥1 时，其反函数y=f-1(x)为D上的AMr+-凸函数.

证明只证（i），同理可证（ii）.

设f(x)是I上的严格递增函数，则f(x)在I上的反函数y=f-1(x)是D上的严格递增函数，∀y1,y2∈D，∃x1,x2∈I，使x1=f-1(y1)，x2=f-1(y2)，所以，y1=f(x1)，y2=f(x2).

当 0＜r≤1时，因为y=f(x)为I上的AM-凸函数，所以，

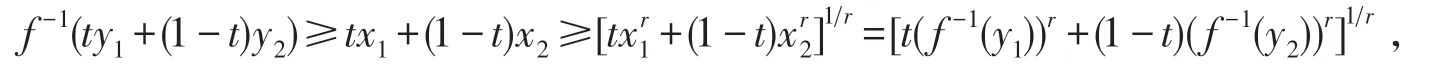
故y=f-1(x)是D上的 AMr+-凹函数.

当r＜0 时，注意到，同理可证，定理8（i）的后半部分成立.

定理9设B⊆I⊆R+,A⊆R+，f:I→R+，μ:A→B，则

（i）若y=f(u)是I上严格递增的rP-凸函数，u=μ(x)是A上的AM-凸函数，则y=f(μ(x))是A上的AM-凸函数；

（ii）若y=f(u)是I上严格递减的rP-凸函数，u=μ(x)为A上的AM-凹函数，则y=f(μ(x))是A上的AM-凸函数；

（iii）若y=f(u)是I上严格递增的rP-凹函数，u=μ(x)为A上的AM-凹函数，则y=f(μ(x))是A上的AM-凹函数；

（iv）若y=f(u)是I上严格递减的rP-凹函数，u=μ(x)为A上的AM-凸函数，则y=f(μ(x))是A上的AM-凹函数.

证明只证（i），同理可证（ii）、（iii）、（iv）.

任取x1,x2∈A，t∈[0,1]，则，tx1+(1-t)x2∈A，

由定理条件知，μ(x1),μ(x2),μ(tx1+(1-t)x2)∈B⊆I，且∀r∈R(r≠0)，亦有

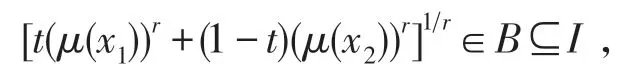
因为u=μ(x)为A上的AM-凸函数，所以，，又y=f(u)是I上严格递增的rP-凸函数，所以

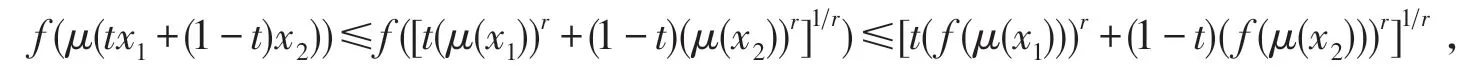
故函数y=f(μ(x))为A上的AM-凸函数.

定理10设B⊆I⊆R+,A⊆R+，f:I→R+，μ:A→B，则

（i）如果y=f(u)是I上严格递增的AM-凸函数，u=μ(x)是A上的凸函数，则y=f(μ(x))是A上的AM-凸函数；

（ii）如果y=f(u)是I上严格递减的AM-凸函数，u=μ(x)为A上的凹函数，则y=f(μ(x))是A上的AM-凸函数；

（iii）如果y=f(u)是I上严格递增的AM-凹函数，u=μ(x)为A上的凹函数，则y=f(μ(x))是A上的AM-凹函数；

（iv）如果y=f(u)是I上严格递减的AM-凹函数，u=μ(x)为A上的凸函数，则y=f(μ(x))是A上的AM-凹函数.

3 AM-凸函数的Jensen型不等式及其应用

定理11设I⊆(0,+∞)，f(x)是定义在I上的AM-凸（凹）函数，则 ∀xi∈I，∀ti∈[0,1](i=1,2,…,n)，且，有

证明若f(x)是I上的AMr+- 凸函数，令φ(x)=(f(x))r(x∈I)，则当r＞0 时，由定理2（i）知，φ(x)为I上的凸函数，因此有凸函数φ(x)在I上的Jensen型不等式

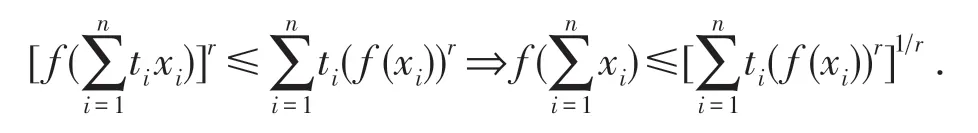
当r＜0 时，同理可证定理仍然成立.

若f(x)在I上是AMr+-凹的，则证明中的不等号反向，所以定理11的后半部分成立.

关于定理11，它的一个等价形式为：

定理12设I⊆(0,+∞)，f(x)为I上的AM-凸（凹）函数，∀xi∈I，∀qi∈R+(i=1,2,…,n)，则

特别地，如果q1=q2=…=qn=1，则有

推论1设I⊆(0,+∞)，f(x)为I上的AM-凸（凹）函数，∀xi∈I(i=1,2,…,n)，则

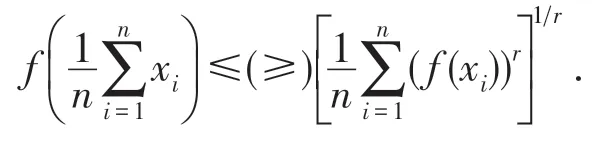
例1设xi∈R+，ti∈[0,1](i=1,2,…,n)，且，证明

证明考察函数f(x)=x(x＞0)，则 (r-1)(f′(x))2+f(x)f″(x)=r-1，

显然，当r≥1 时，(r-1)(f′(x))2+f(x)f″(x)≥0，由定理 4 知，函数f(x)=x(x＞ 0)是 AMr+-凸函数，将f(x)=x(x＞0)代人定理11（8）式，得

由上述证明过程可知，当r≤1时，不等式（9）成立.

注2：在不等式（10）中，取r=0 即为著名的加权算术-几何平均不等式：

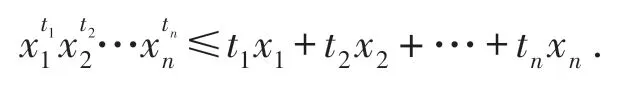
［1］HARDY G H，LITTLEWOOD J E，PÓLYA G.Inequalities［M］.Lundon：Cambridge University Press，1952.

［2］MITRINOVIC D S，VASIC P M.Analytic inequalities［M］.Berlin：Springer-Verlag，1970.

［3］王伯英.控制不等式基础［M］.北京：北京师范大学出版社，1990.

［4］吴善和.几何凸函数与琴生型不等式［J］.数学的实践与认识，2004，34（2）：157-163.

［5］吴善和.调和凸函数与琴生型不等式［J］.四川师范大学学报：自然科学版，2004,27（4）：382-386.

［6］吴善和.平方凸函数与琴生型不等式［J］.首都师范大学学报：自然科学版，2005,26（1）：16-21.

［7］吴善和.对数凸函数与琴生型不等式［J］.高等数学研究，2004，7（5）：61-64.

［8］陈少元.AH-凸函数及其应用［J］.湖北职业技术学院学报，2013，16（2）：106-109.

［9］吴善和.GA-凸函数与琴生型不等式［J］.贵州师范大学学报：自然科学版，2004,22（2）：52-55.

［10］陈少元.GH-凸函数及其Jensen型不等式［J］.首都师范大学学报：自然科学版，2013（5）：1-5.

［11］宋振云.HA-凸函数及其Jensen不等式［J］.德州学院学报，2014，30（4）：16-21.

［12］陈少元.HG-凸函数及其Jensen型不等式［J］.数学的实践与认识，2013，43（2）：257-264.

［13］吴善和.rP-凸函数与琴生型不等式［J］.数学的实践与认识，2005,35（3）：220-228.

［14］张孔生，万建平.P-凸函数及其性质［J］.纯粹数学与应用数学，2007，23（1）：130-133.

［15］宋振云.MG-凸函数及其Jensen不等式［J］.山东师范大学学报：自然科学版，2014，30（4）：56-60.

［16］宋振云，陈少元.GM-凸函数及其Jensen不等式［J］.数学的实践与认识，2014，44（20）：280-287.

［17］匡继昌.常用不等式［M］.4版.济南：山东科学技术出版社，2010.

［18］刘建忠.Cauchy不等式和Kantorvich不等式的推广［J］.河北大学学报：自然科学版，2004，24（3）：240-242.

［19］罗俊丽.关于Minkowski不等式的一个新推广［J］.延安大学学报：自然科学版，2006,25（2）：12-13.