构造法在线性代数教学中的应用

陈冬君，张 云

（淮北师范大学 数学科学学院，安徽 淮北 235000）

所谓构造法就是在研究有关数学问题时，需要构造并解出一个合适的辅助问题，从而用它来求得一条通向表面看来难于接近问题的通道的一种解答问题的方法.构造法是解决数学问题的一种基本且行之有效的方法，具有两个特点，即直观性和有效性.历史上利用构造法解决数学难题的例子层出不穷，例如古希腊数学家欧几里得利用构造法巧妙给出数论中最基本定理“素数的个数是无穷的”：又如，瑞士数学家欧拉利用构造图论的模型解决著名的哥尼斯堡七桥问题.目前，构造法在各个数学专业课程方面的教学研究论文很多，见文献［1-4］.

数学菲尔兹奖得主丘成桐博士曾经说过，“不等式是分析的精华”.不等式在数学研究中的地位和作用可见一斑.本文主要目的是在线性代数的观点下，通过恰当合理地构造矩阵且结合矩阵的特征值、奇异值等一些经典结果给出一些经典不等式的简洁证明，从而体会在线性代数的观点下，让学生感受到构造法在证明一些经典不等式中的精妙之处.

首先给出关于矩阵的一些基本概念和定理.

我们用Cn和Rn分别表示全体n维复向量和实向量组成的线性空间.记Mm,n为m×n阶复矩阵的全体，特别地，Mn,n被简记为Mn表示n阶方阵的全体.用Hn表示n阶Hermite矩阵构成的集合，对于A∈Hn总是将它的特征值按降序排列并记为λ1(A)≥λ2(A)≥…≥λn(A)且记λ(A):=(λ1(A),…,λn(A)).A∈Mn的奇异值定义为A*A的特征值的非负平方根，称为A的绝对值，因此A的奇异值就是|A|的特征值.我们总是用s1(A)≥s2(A)≥…≥sn(A)表示A∈Mn的奇异值且记s(A):=(s1(A),(s2(A),…,sn(A)).对于任意的A∈Mn及任意的酉矩阵U,V∈Mn，有s(UAV)=s(A).因此，对于正规矩阵而言，它的奇异值就是它的特征值的模.特别地，对于半正定矩阵，奇异值和特征值是一样的.

用表示n维非负实向量.在本文的多数情形下将Rn中的向量看成是行向量.但是，当它们和矩阵相乘时则被看成是列向量，这种差别联系上下文可以看出，不会引起混淆.将向量x=(x1,x2,…,xn)∈Rn的分量重新排序为x[1]≥x[2]≥…≥x[n].下面给出向量的优超和对数优超的概念［5-6］.

设x=(x1,x2,…,xn),y=(y1,y2,…,yn)∈Rn，若

则称x被y弱优超，记为x≺wy.若x≺wy可且则称x被y优超，记为x≺y.

设x=(x1,x2,…,xn),y=(y1,y2,…,yn)∈，若

则称x被y弱对数优超，记为x≺wlogy，若x≺wlogy且，则称x被y对数优超，记为x≺logy.

1 构造矩阵巧证加强的算术-几何平均值不等式

一个熟知的事实是弱对数优超蕴涵弱优超，

引理1［5-6］设x,y∈.则

引理2［5-6］设n阶方阵A的特征值为λ1,λ2,…,λn.则

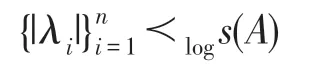
回顾算术-几何平均值不等式的内容：对任意的n个正实数x1,x2,…,xn，都有

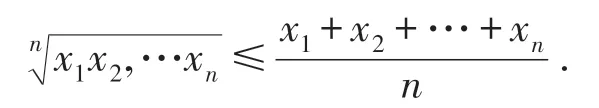
利用构造法给出如下的加强版本的算术-几何平均值不等式.

定理3对任意的n个正实数x1,x2,…,xn，且x1≥x2≥…≥xn，则对于任意的正整数k，满足1≤k≤n都有

证明构造n阶方阵A满足在(i,i+1)位置的元素为xi,i=1,2,…,n-1和(n,1)位置的元素为xn，其余位置的元素都为0.通过直接计算可得，它的每个特征值的模都相等且都为

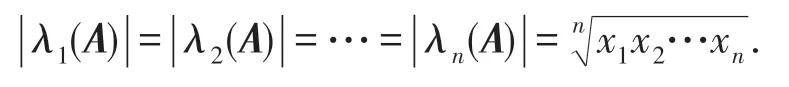
另一方面，根据奇异值的酉不变性，即对于任意的A∈Mn及任意的酉矩阵U,V∈Mn，有s(UAV)=s(A).容易知道s(A)=(x1,x2,…,xn).根据引理2知

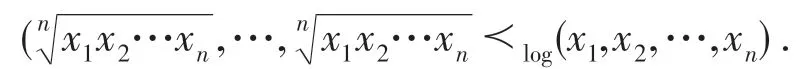
容易验证上述对数优超不等式中的两个向量都属于.因此，由引理1可得

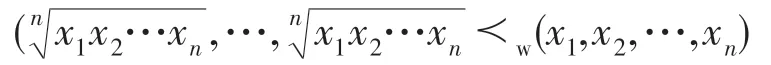
由弱优超的定义知，不等式（3）得证.证毕.

推论4对任意的n个正实数x1,x2,…,xn，且x1≥x2≥…≥xn，则对于任意的正整数k，满足1≤k≤n都有

证明根据定理3的证明过程知，

由对数优超的定义知，不等式（4）得证，证毕.

2 构造矩阵巧证置换不等式

引理5［5-6］设A和B是任意的两个n阶方阵，则

定理6设x1≥x2≥…≥xn≥0,y1≥y2≥…≥yn≥0.若 π(1),π(2),…,π(n)是1，2，…，n的任意置换，则对于任意的正整数k，满足1≤k≤n都有

证明设 π(1),π(2),…,π(n)是l，2，…，n的任意给定置换.构造n阶对角矩阵A满足

和n阶对角矩阵B满足

直接计算可得，

由引理5知，不等式（5）得证.证毕.

注1记当k=n时，即为［3］中引理3.3的结果.

3 结束语

构造法已经广泛应用于数学研究之中，该方法使用得当能够起到将问题化繁为简、化难为易的作用.文中利用构造矩阵的方法结合线性代数中矩阵的优超理论给出两个新的不等式的证明.通过构造法的训练能够让我们拓宽研究的思路，加强对数学概念的理解，逐步让学生体会数学的美妙之处，文章通过这些例子，让学生体会如何恰当使用构造法解决问题，培养学生的创新思维，提高学生的数学修养.让学生通过线性代数的学习，逐步看到线性代数在解决数学问题的作用，增强学生学习该课程的积极性和主动性，提高该课程的教学质量.

［1］朱爱玲.构造法在计算方法教学中的应用［J］.山东师范大学学报（自然科学版），2008（2）：12 5-126.

［2］刘银萍.构造法在高等数学教学中的应用［J］.吉林师范大学学报（自然科学版），2006（3）：85-86.

［3］李家彬.浅析用构造法解数学题［J］.云南大学学报（自然科学版），2009（2）：551-554.

［4］邬洪涛，何平.构造法在高等数学解题中的应用［J］.长春理工大学学报（高教版），2009（11）：84-85.

［5］HORN R A，JOHNSON C R.Topics in Matrix Analysis［M］.Cambridge:Cambridge University Press，1991.

［6］ZHAN X.Matrix Theory，Graduate Studies in Mathematics 147［M］.American Mathematical Society，Providence R I，2013.

［7］孙继广.矩阵扰动分析［M］.北京：科学出版社，2001.