一类非线性微分方程耦合系统无穷边值问题解的存在性

张海燕，李耀红

（宿州学院 数学与统计学院，安徽 宿州 234000）

令（E，‖·‖）是Banach空间，考虑E中一阶非线性微分方程耦合系统无穷边值问题：

这里J=[0 ,+∞),f,g∈C[J×E×E,E],α,β＞ 1.

近年来，微分方程耦合系统受到广泛关注，获得许多有价值的结果.如在无穷区间上，文［1-4］获得了微分方程耦合系统解的存在性或多解性；在分数阶情形下，文［5-8］也获得许多微分方程耦合系统的可解性结论.但上述文献中微分方程系统的耦合性主要是指非线性项中变量的耦合，对边值条件的耦合性研究相对较少.注意到耦合边值条件在反扩散问题、热学问题、流体力学等应用科学领域有着广泛的应用.本文将利用Mönch不动点定理，结合一个新的比较结果，研究非线性微分方程耦合系统无穷边值问题（1），其非线性项和边值条件均具有耦合性.

1 预备知识和引理

记C［J，E］={u：J→E|u（t）连续}，C1［J，E］={u：J→E|u（t）连续且一阶可微}.令BC［J，E］={u∈C［J，E］|X=BC[J,E]×BC[J,E], 则 易 知BC[J,E]和X分 别 在 范 数和‖(u,v)‖X=‖u‖B+‖v‖B下为一Banach空间.定义算子T：X→X如下

其中

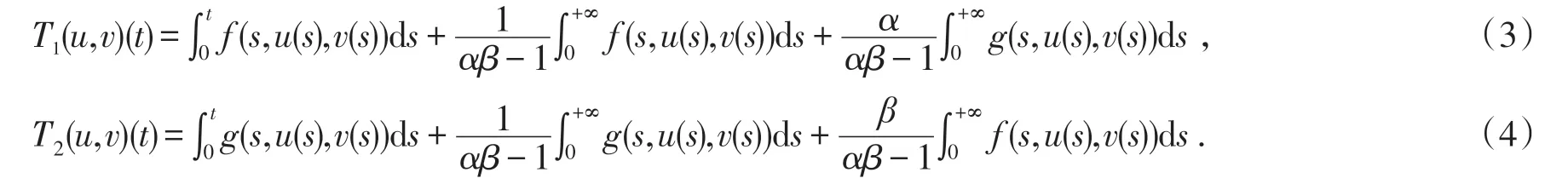
若（u，v）∈X且满足（1），则称（u，v）为边值问题（1）的解.对Banach空间中的有界集C，用α（C）衷示Ku⁃ratowski非紧性测度［9］.另记Br={(u,v)∈X|‖ (u,v‖X≤r}(r＞ 0).

为方便下文，给出几个需要用到的引理.

引理1若f,g∈C[J×E×E,E]，则 (u,v)∈BC[J,E]⋂C1[J,E]×BC[J,E]⋂C1[J,E]是耦合系统（1）的解有且仅当(u,v)是T(u,v)=(u,v)在X中的不动点.

证明若(u,v)是耦合系统（1）的解，则直接对耦合系统（1）前两式两边直接从0到t积分，可知

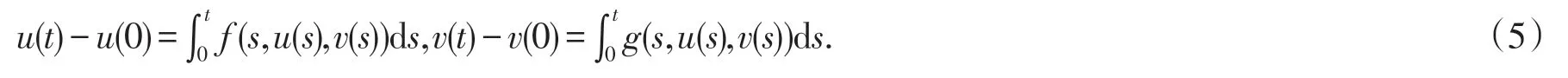
令t➝∞，则有

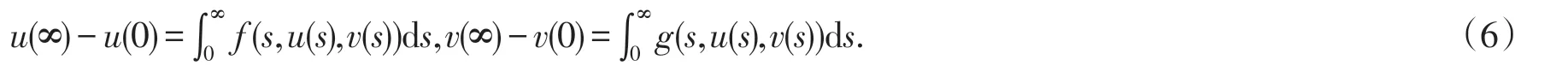
将边值条件u(∞)=αv(0),v(∞)=βu(0)代入式（6），直接解方程组计算可知

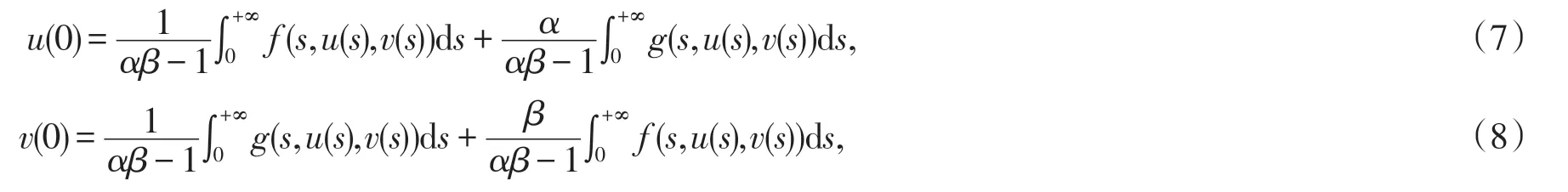
将式（7）（8）代入式（5），易知u(t)=T1(u,v),v(t)=T2(u,v)，即 (u,v)是T(u,v)=(u,v)的不动点.反之，若 (u,v)是T(u,v)=(u,v)的不动点，则对等式两边求导，容易验证(u,v)满足系统（1）.命题得证.

引理2［2］若m(t),γ(t)∈C[J,J],m(t)是有界函数，，且有

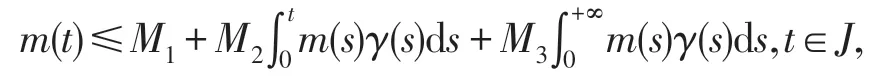
其中M1≥0,M2,M3＞0，则

引理 3［9］若H是C[J0,E](J0=[0,b]⊂J)中的可数可测集，对任给x∈H，存在ρ(t)∈L[J0,J]，使得‖x(t)‖≤ρ(t),t∈J0，则有α(H(t))∈L[J0,J]，且

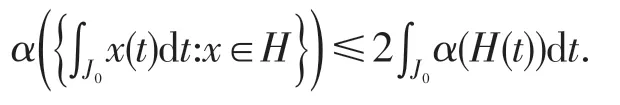
引理4［10］若B={un}⊂C[J,E](n=1,2,…)，存在ρ(t)∈L[J,J]，使得 ‖u‖n(t)≤ρ(t)(t∈J,n=1,2,…)，则有α(B(t))在J上可积，并且

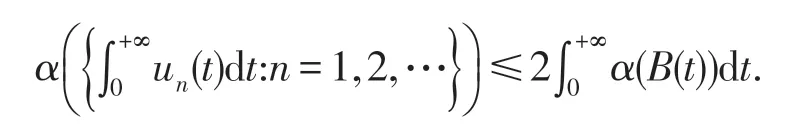
引理5［10］设下文（A1）成立，H是E中的有界集，则，其中αE(TiH)表示TiH(i=1,2)在E中的非紧性测度.

注1由（2）式及引理5易知，αE(TH)≤αE(T1H)+αE(T2H).

引理6［11］（Mönch定理）设E是Banach空间，Ω⊂E是有界开集，θ∈Ω,A:E→E是一个连续算子，且满足下列条件：

（1）x≠λAx,∀λ∈[0,1],x∈ ∂Ω；

（2）由H⊂可数及H⊂({θ}⋃A(H))可推出H为相对紧集.则A在Q中至少有一个不动点.

引理7［12］设D和F是E中的有界集，则α(D×F)=max{α(D),α(F)}，其中α和α分别为E×E和E中的Kuratowski非紧性测度.

2 主要定理

为方便，先给出下列假设：

（A1）f,g∈C[J×E×E,E]，且存在ai(t),bi(t)∈L[J,J](i=1,2,3)，使得

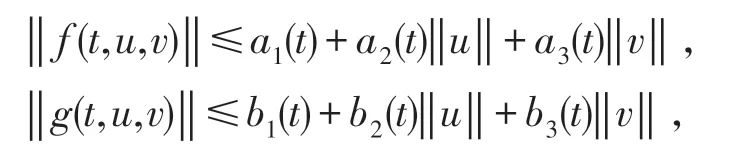
（A2）对 ∀t∈J和H1,H2⊂Br，存在ci(t),di(t)∈L[J,J](i=1,2)，使得

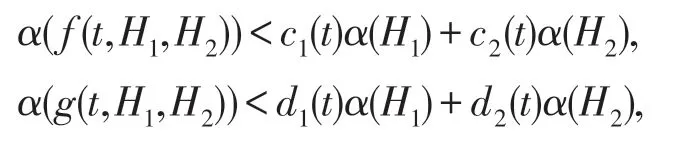
定理1若条件（A1）-（A2）成立，则耦合系统（1）在BC[J,E]⋂C1[J,E]×BC[J,E]⋂C1[J,E]中至少有一个解.

证明由引理l知，只需证明算子T在X中至少有一个不动点.首先证明

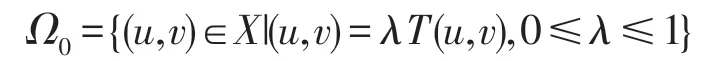
是X中的有界集.事实上，对任给的(u,v)∈Ω0，则相应地存在0≤λ0≤1，使得

当t∈J=[0,+∞)时，由式（3）（4）（9）及假设（A1）得

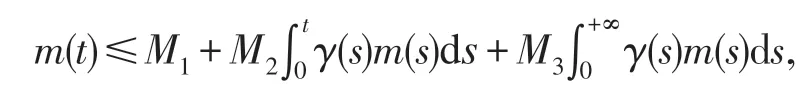
故由引理2知

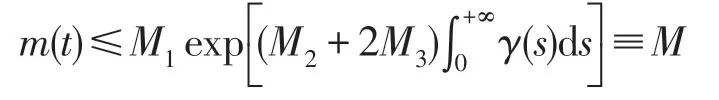
令R＞M，取

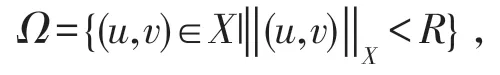
则Ω是X中的有界开集，且(θ,θ)∈Ω.由R的取法可知，对任何(u,v)∈∂Ω,(u,v)≠λT(u,v),∀λ∈[0,1].即引理6的条件（1）满足.

下面验证引理6 的条件（2）满足.设H⊂为可数集且由非紧性测度的性质，结合引理3-4，引理7及假设（A2），可知

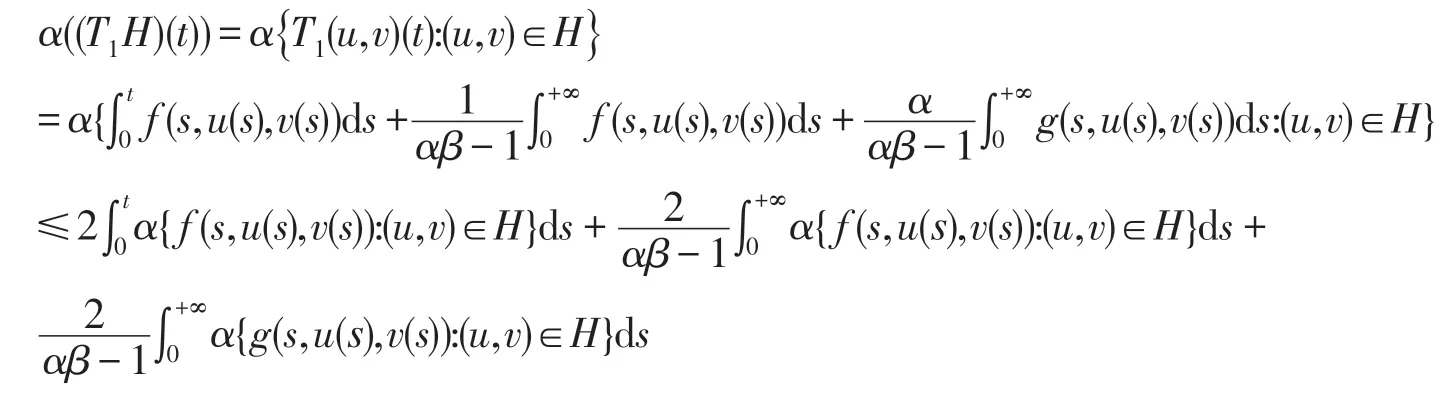
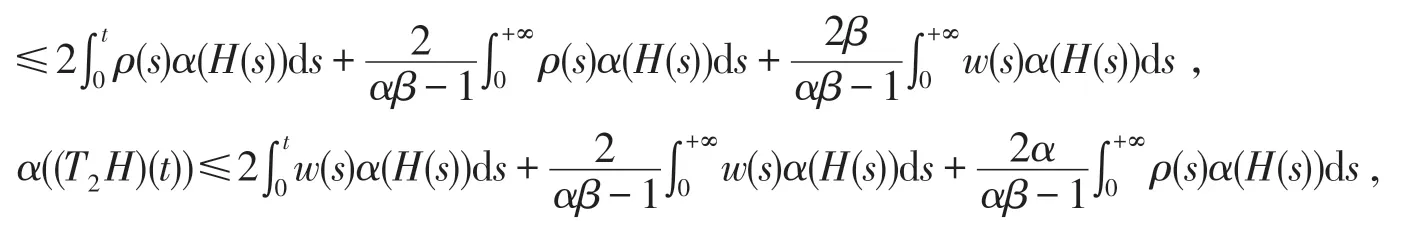
这里ρ(s)=c1(s)+c2(s),w(s)=d1(s)+d2(s).

由H的定义及引理5有

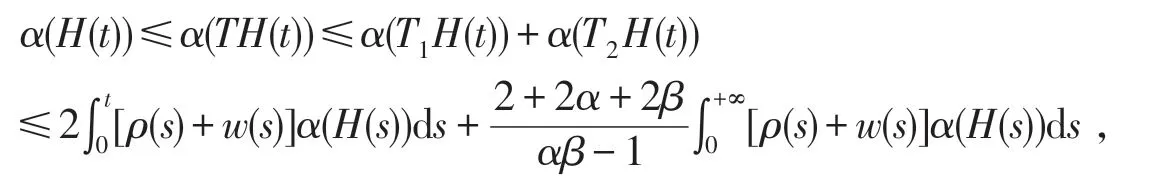
于是由引理l知，α(H(t))=0,t∈J.即H是Ω中的相对紧集，于是引理6的条件（2）满足.又注意f,g的连续性，显然T是连续算子.故由引理6知，算子T在Ω内至少有一个不动点.从而耦合系统无穷边值问题（1）至少有一个解.证毕.

例1考虑一阶非线性微分方程耦合系统无穷边值问题：

则耦合系统无穷边值问题（12）至少有一个解.

证明令E={x=(x1,x2,…,xn,…)|xn∈J,xn→0}，对x∈E，令显然耦合系统（12）可转化为X中的系统

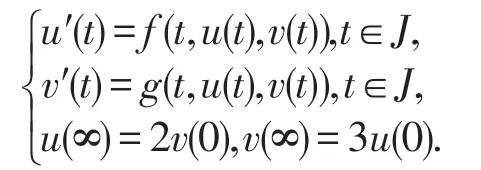
其中

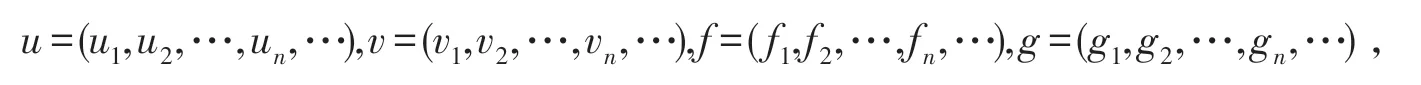
而

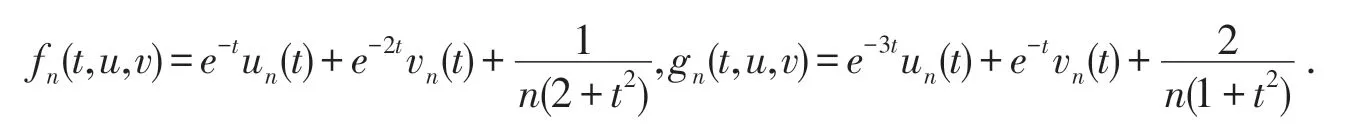
显然f,g∈C[J×E×E,E].

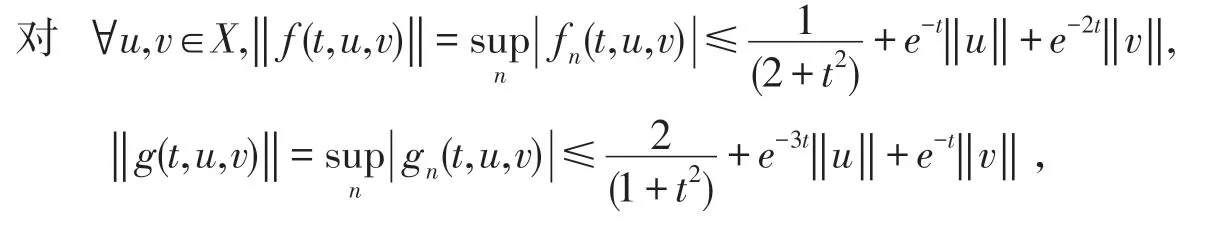
则可令

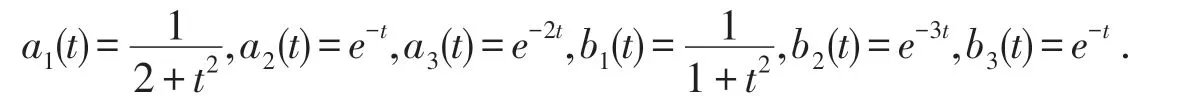
［1］CHEN Xu，ZHANG Xingqiu.Existence of positive solutions for singular impulsive differential equations with integral boundary conditions on an infinite interval in Banach spaces［J］.Electron J Qual Theory Differ Eq，2011（29）：1-18.

［2］张海燕，张祖峰.Banach 空间中一阶非线性微分方程组无穷边值问题解的存在性［J］.华中师范大学学报（自然科学版），2011，45（4）：529-533.

［3］汤小松，王志伟，罗节英.Banach空间中一阶脉冲微分方程组的无穷边值问题解的存在性唯一性［J］.四川师范大学学报（自然科学版），2012，35（6）：802-808.

［4］李耀红，张祖峰.无穷区间上一阶非线性脉冲微分方程组边值问题的多个正解［J］.华中师范大学学报（自然科学版），2014，48（2）：171-175.

［5］LI Yaohong，WEI Zhongli.Positive solutions for a coupled systems of mixed higher-order nonlinear singular fraction⁃al differential equations［J］.Fixed Point Theory，2014，15（1）：167-178.

［6］申腾飞，宋文耀.一类分数阶微分方程系统边值问题正解的存在性［J］.常熟理工学院学报，2012，26（4）：28-34.

［7］程玲玲，刘文斌.带有p-Laplace 算子分数阶微分方程耦合系统边值问题解的存在性［J］.湖北大学学报（自然科学版），2013（1）：48-51.

［8］曹竞文，胡卫敏.两点分数阶微分方程耦合系统边值问题的解［J］.江汉大学学报（自然科学版），2014，42（3）：23-26.

［9］GUO Dajun，LAKSHMIKANTHAM V，LIU Xinzhi.Nonlinear integral equations in abstract spaces［M］.Dordrecht：Kluwer Academic Publisher，1996.

［10］刘振斌，刘立山.Banach 空间中一阶非线性微分方程组无穷边值问题解的存在性［J］.数学学报，2007，50（1）：97-104.

［11］DEIMLING Klaus.Nonlinear functional analysis［M］.Berlin：Spring-Verlag，1985.

［12］GUO Dajun，LAKSHMIKANTHAM V.Coupled fixed points of nonlinear operators with applications［J］.Nonlinear Analy⁃sis：TMA，1987，11（5）：623-632.