解含有参数函数单调性的有效研究

北京市通州区永乐店中学 李龙强

含有参数函数的单调性在高考中是一类热点问题，这类问题，从知识层面上看，主要考查了函数单调性与导数的关系；从数学方法上看，主要考查等价转化，数形结合，分类讨论思想。针对在教学过程中学生对于含有参数函数的单调性问题无从下手，笔者把这类问题的常用解法整理一下，希望对读者能够起到抛砖引玉的效果。

纵观近几年北京卷理科高考试题，笔者认为：导数的解答题，无论试题的内容与形式进行怎样的变化，但是离不开研究函数单调性，利用函数单调性研究问题。

一、解形如ax+b＞0的不等式

通过移项得ax＞-b，在这里需要讨论一次项系数a与0的关系。如果a＞0，那么如果a＜0，那么如果a=0，那么原不等式转化成0＞-b，若b≥0，则x∈R，若b＜0，则x∈φ．

1、（2009 北京理，18）设函数f（x）=xekx（k≠0）．

（Ⅱ）求函数f（x）的单调区间．

解：函数f（x）的定义域是R，

由f′（x）=（1+kx）ekx=0，得

若k＞0，则当时， f′（x）＜0，函数f（x）单调递减，

当时，f′（x）＞0，函数f（x）单调递增，

若k＜0，则当时，f′（x）＞0，函数f（x）单调递增，

当时，f′（x）＜0，函数f（x）单调递减．

二、解形如ax2+bx+c＞0的不等式

首先关注二次项系数a是否等于0，若a=0，则不等式解法如上一所示；若a≠0，其次关注不等式左侧多项式能否分解因式，如果能够分解因式，直接求出两根，根据两根大小，再利用一元二次函数图象，采用数形结合思想解出不等式；如果不等式左侧多项式不能分解因式，再次利用一元二次方程根的判别式来解不等式．

1、（2012 北京理，18）已知函数f（x）=ax2+1（a＞0），g（x）=x3+bx

（2）当a2=4b时，求函数f（x）+g（x）的单调区间．

解：由题设a2=4b，设

函数h(x)的定义域是R，

则

∵a＞0，

h′（x）h（x）随x的变化情况如下：

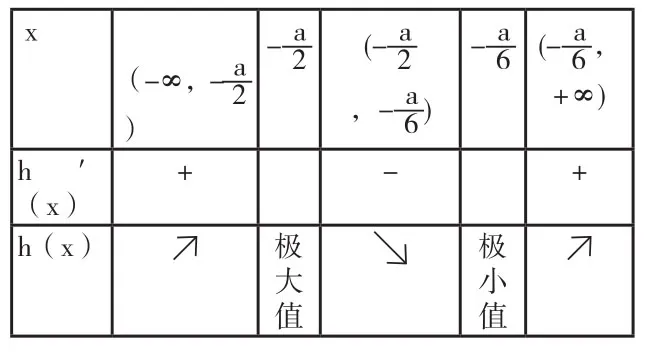
x -a 2(-a 2-a 6(-a 6，（-∞，-a 2，-a 6)）+∞)h ′（x）+-+h（x）极大值极小值

所以函数h(x)的单调递增区间为

三、解分式

单调递减区间为＞0不等式应将分式不等式等价转化为整式不等式，

即：

然后用“根轴法”或化为不等式组求解.

通过图1所示的调整方法，分别对决策信息以及与进行冲突水平判定与调整，使群决策信息的冲突水平在合理的范围。为便于表述，仍令具有调整后的、具有合理冲突水平的决策信息为与

四、解指数不等式、对数不等式、三角不等式（含参）

1、（2014 北京理，18）已知函数

上恒成立，求a的最大值与b的最小值.

解：（2）当 0x≻ 时，“等价于“sin x−ax≻0”“

（2）若在”等价于“sin x−bx≺0”。

令 g( x)=sin x−cx，则g'(x)=cosx− c，当0c≤时，()0g x≻ 对任意恒成立。

当 1c≥时，因为对任意g'(x)=cosx −c ≺0，所以g(x)在区间上单调递减。从而g(x)(0)0g=≺对任意恒成立。

当01c≺≺时，存在唯一的

使得 g'( x0)= cosx0−c =0。

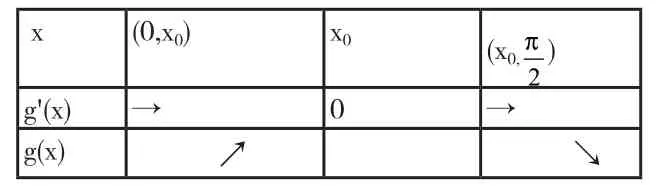
x (0,x0) x0 (x0,π)2 g'(x) → 0 →g(x) ↗ ↘

因 为 g( x)在区间[0 ,x0]上是增函数，所以 g( x0) ≻g(0)=0。进一步，“() 0g x≻ 对任意恒成立”当且仅当即

综上所述，当且仅当时，g(x)≻0对任意恒成立；当且仅当 1c≥时，g( x) ≺ 0对任意恒成立。

所以，若对任意恒成立，则a最大值为b的最小值为1.

五、时刻关注函数定义域，对于解不等式起到画龙点睛的作用

1、已知函数求f(x)的单调区间．

解：f(x) 的定义域为（0，+∞），

令f′(x)＝0得x=-a

若a≥0，f′(x)≥0恒成立，所以（0，+∞）为函数f(x)的增区间；

若a＜0，令f′(x)＞0，解得x＞-a

令f′(x)＜0,解得x＜-a

综上所述：

当a≥0（0，+∞）为函数f(x)的增区间；

当a＜0，（-a，+∞)为函数f(x)的增区间 ，

（0，-a)为函数f(x)的减区间。

解不等式的过程，实质上是同解不等式逐步代换化简原不等式的过程，因而保持同解变形就成为解不等式应遵循的主要原则，实际上高中阶段所解的不等式最后都要转化为一元一次不等式、一元二次不等式、指数不等式、对数不等式、三角不等式等.所以等价转化是解不等式的主要思路.为此，一要能熟练准确地解基本不等式，二要保证每步转化都要是等价变形.