基于切比雪夫最佳逼近意义下的CPI指数变化通道的原理与方法＊

顾乐民

（同济大学 材料科学与工程学院，上海 200092）

1 引 言

居民消费价格指数（Consumer Price Index，简称CPI指数），是普通消费者所购买的物品与劳务的总费用的衡量标准，反映了一定时期内价格变动程度和趋势的相对数．CPI指数不仅受商品价格的影响，比如粮价［1］、房价［2］等，也有对其权重经常进行调整的一个动态过程，这使得CPI指数变化具有随机性大、难以找到一般变化规律、难以进行预测等特征．对CPI预测理论及方法成为许多学者关注的问题，目前主要有，基于小波分解自回归模型分析法［3］、VAR 模型法［4］、ARIMA 模型法［5］、神经网络法［6］、灰色 GM（1，1）模型法［7］等．

2000年以来的CPI指数积累了186组数据，数据是离散的，孤立的，数据之间的关系是不明确的，数据的来源是有一定统计误差的．这些看似杂乱无章的数据背后，仿佛总有一只无形的手在操纵着CPI数据的变化，称这只无形的手为“隐函数”．或许这只无形的手根本就不存在，因为CPI指数的波动含有大量的“人类因素”，或许存在但目前难以找到，但这不影响探讨的本质．任何一个运动、变化、发展的事物，都存在其本质的内在规律，都是可以从变化的过程中找到．

构建隐函数的目的，是要用数学的方法来探索CPI变化的某些规律．CPI指数属于一种“近程有序，远程无序”的数据变化形式，在较短的局部范围内，其变化具有一定的规律可循．从长期全局范围看，其变化呈大波动状失去规律．这也就是说，用具有轨迹特征的曲线是难以描述这种变化的，必须用其它的方法，一种既包含着曲线又不局限于曲线的方法去描述．

切比雪夫（P．L．Chebyshev，1821～1894）创立的最佳一致逼近原理，最早源于19世纪对机器的机械运动按理想设计运动的研究．将该原理运用于CPI指数变化，可以构建一条切比雪夫最佳逼近意义下的CPI指数变化通道．CPI指数变化是有限的变化，可以用2条曲线，1条称为上界限，另1条称为下界限，将所有的数据都囊括其中，并形成一条延伸的通道．通道将杂乱无章的数据加以规范和约束，而隐函数必定在通道之内，通过数学的方法可以找到最佳逼近意义下的隐函数，使CPI的变化成为可知与可控．由于通道具有连续性，变化具有惯性，所以通道的外延具有一定的预测效应，可以推断出未来可能的变化趋势，为决策提供有价值的参考．

切比雪夫最佳逼近意义下的数据通道的建立与应用，文献［8］有较为详细的描述．由于CPI指数具有变化莫测的特殊性，从最简单的“直线通道”入手，通过建立通道而阐述其基本的原理与方法，并用186组数据按序做30个数据处理的实例，以检验预测的效果．

2 原理与方法

切比雪夫最佳逼近的核心是最大绝对值误差极小化，由此构成了极小极大曲线拟合法，适用于一个封闭系统内的描述，具有广泛的应用［9］．由于最大误差一般都是在端点处出现，在定义区间外是发散的，这从切比雪夫多项式的所有图形中可以看出，所以不适合用于预测．对预测而言，预测的误差越小越好，而不是最大甚至发散．零误差型极小极大逼近是切比雪夫最佳逼近原理的一个推广，是通过若干零误差点限制端点误差为最大，达到端点外误差不发散的目的，其理论基础是零误差型切比雪夫多项式［10］，以及相应的预测理论［11］．对于 CPI指数的预测，只需提供1个零误差点，在坐标系上是指最右端（简称端点，下同）的数据点，这使复杂的问题可以简化叙述．

2．1 零误差型极小极大法（Z－Minimax method）

数据 （xi，yi）i＝1，2，…，m是隐函数y（x）在有定义的区间内给出的m个离散点组，为找到隐函数y（x），设拟合函数f（x）＝f（x，a），其中参数a＝（a1，a2，…，an），n≤m，而a1，a2，…，an为n个不全为零的实数．为使f（x）尽可能接近y（x），设误差函数r（x）＝y（x）－f（x），而误差值ri是误差函数r（x）上的具体数值：

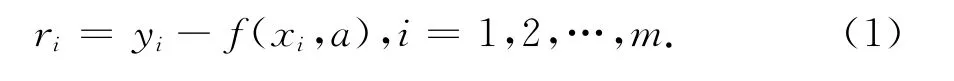
零误差型极小极大法，是将端点数据误差设定为零误差rm＝0条件下，依据最大绝对值误差极小化的准则来选择参数a，即依据而构成的一种方法，是切比雪夫最大绝对值误差极小化基本准则的一个推广．

2．2 解的实现

如果零误差型极小极大解存在，即存在a＝a＊使

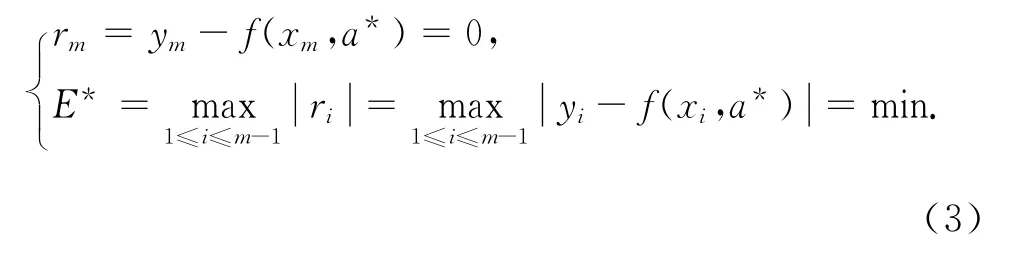
则至少存在1个零误差点和n个切比雪夫交错点x1，x2，…，xn使

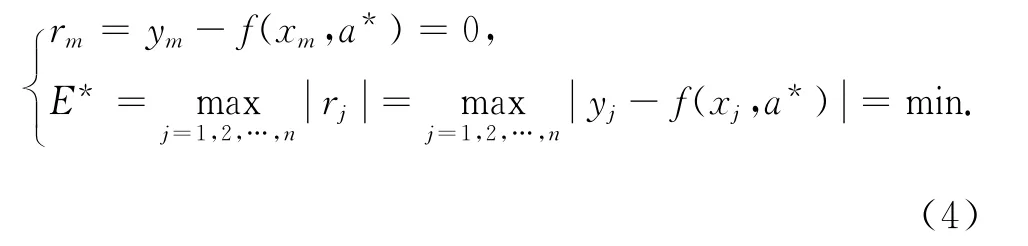
称参数a＊为极小极大最佳拟合参数，称f（xj，a＊）为极小极大最佳拟合方程，称E＊为最佳逼近值，它们构成了零误差型极小极大逼近的一般解．

2．3 零误差

所谓零误差就是没有误差或误差为零．当将端点数据的误差设定为零时，可使短期的预测得到保证．从曲线变化的一般规律来看，零误差的两端是以“－，0，＋”或“＋，0，－”形式出现，越接近零点，误差绝对值就越小．这就给出一个提示，将端点误差设定为零误差即ym－f（xm）＝0，则对于端点外临近的数据，其预测误差rm＋1＝ym＋1－f（xm＋1）的绝对值也必定不会大，这为预测的准确性提供了理论依据，仅在出现大随机误差的特例下才会无法成立［11］．

2．4 CPI通道

某个变化的过程和状态可用“通道”来描述，例如，处于下降（或上升）的通道之中等．通道，来往畅通的道路，与交通图中的道路相似，是拟人化的表达．零误差型极小极大逼近意义下的CPI指数变化通道，简称CPI通道（下同）有以下几个特征：

1）通道的构成．通道由1条中心线，2条边界线共同构建；中心线是CPI函数转化的曲线，也称为路线是前行的指导线；边界线是距中心线两旁±E的曲线．通道用Channel（x）表示：

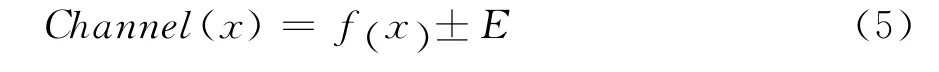
2）通道的作用．通道将离散的、有随机误差的数据加以分类和规范，它依据最佳逼近值±E将全部的数据规范在通道内，指出了位于边界线上的数据，由于偏离中心线最远，属于波动最大的大误差数据；通道将端点数据的误差设定为零误差，废除了所有数据是权重相等的惯例，使权重往端点数据倾斜，并使对未来的预测建立在零误差的基础上；通道包含了所有的数据，所以隐函数必定在通道内，通过数学方法可以找到最佳逼近意义下的隐函数，或近似隐函数．

3）通道的意义．将理论的指导路线与实际行走的轨迹联系在一起，数据沿着中心线前行，但实际是在偏离和纠正偏离中前行的；通道指出了数据变化的最大范围，限定了安全的最大界线；在最大安全范围内去探寻隐函数，从而找到CPI变化的某些规律，用于解释过于、指导现在、预测未来．

3 具体算法

由于CPI数据的随机性，波动性，难预测性，用通道的原理和方法寻找数据之间的关系有较好的效果．下面用图示法加以介绍，用的是直线型通道．图1横坐标x是月，纵坐标y是CPI指数值（无量纲）．图中参与计算的CPI数据yi是12个，均在虚线之内，虚线外的数据有1个，不参与计算．

3．1 通道的构成

通道的中心线是拟合函数描述f（x）＝f（x，a），与2条边界线共同构建成通道f（x）±E．通道内包含了12个数据．由式（4）产生的最大正负误差点位于边界线上，如图1中的点A和点B．通道内有1个零误差点，位于数据的端点，如图1中的点C．

3．2 零误差点

零误差点是人为设置的点，目的有3个：首先是将相等权重的数据变为不等权重，一般而言，距离现在最近的数据应该有较大的权重，而较远的权重可以较小，这对于预测而言是合理的，所以端点数据是权重最大的数据．其次是使未来的预测建立在误差为零的基础上，这对于未来的预测误差，难以判断是正还是负而言，是合理的．再次是一般在零点附近的数据其误差绝对值一般都是较小的，这使短期预测准确性有了理论上的依据．

3．3 边界线

大误差数据的出现，会使边界线外移，使通道变宽．为使通道收窄，必须将最大（正负）误差极小化．图中由点A和点B的这2个最大误差又都是极小化的，所以边界线也是极小化的，使通道收窄．从安全意义上说，切比雪夫最佳逼近意义下的通道，是最窄的通道，也是数据变化的最大安全范围，超出这个范围就有可能是不安全或欠安全的．

3．4 预测假设条件

若未来短期CPI指数的变化不存在突变，或存在突变但其最大绝对误差不大于通道内的最大绝对值误差，则通道的外推延伸能较好的给出未来CPI指数变化的趋势．预测是建立在预测值f（xm＋1）与最大正负误差±E基础上的，描述了CPI指数未来可能的数值与最大的波动范围：f（xm＋1）±E．从统计概率角度出发，大部分变化不会超出f（xm＋1）±E，这样就使得CPI指数未来的变化成为可知与可控．

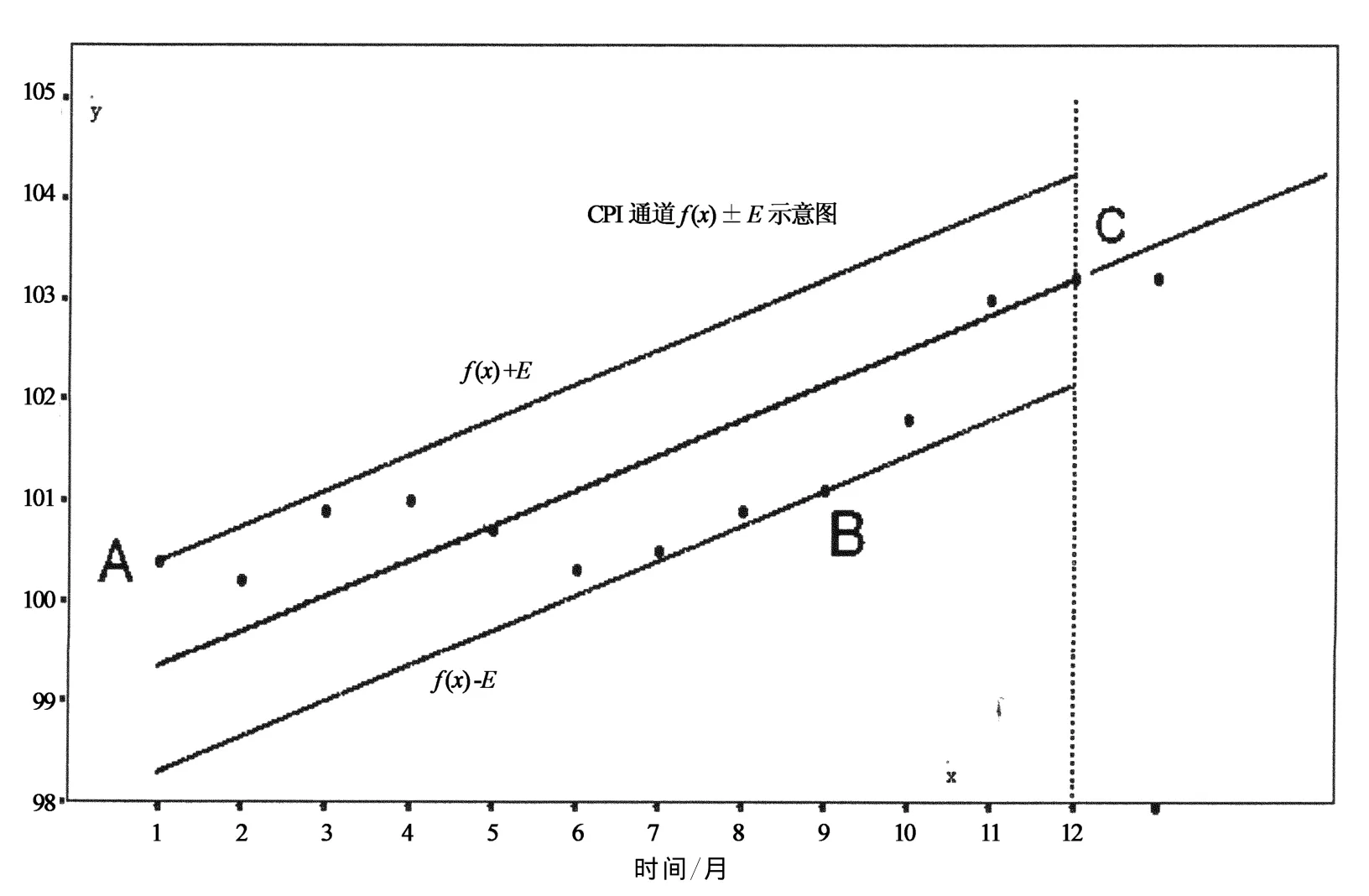
图1 CPI指数变化通道示意图

3．5 判断法则与具体算法

判断法则主要是判断异常解是否存在，以及如何处理的问题．

最大绝对值误差与最小绝对值误差（即零误差）之间在本质上是不相容的，强制将原本是最大误差的端点改为零误差点，会导致方程结构大的改变，甚至会使方程出现一种病态状，结果是预测准确性变差．异常解出现的原因一般在于数据的随机性偏大，数学模型选择的不当所致．具体算法包含判断法则，主要步骤如下．

1）判断：先用最小二乘法对数据进行预处理，进行判断．若用最小二乘法的数据处理，其最大绝对值误差出现在端点，且该误差值较其他误差值明显放大，则该点就是异常数据点，其解将可能会出现异常．最小二乘法是个简单方便的数据处理法，它所获得的最大绝对值误差一般也是极小极大法的最大绝对值误差，所以用最小二乘法进行预处理，用的是其方便与有效．

2）处理：对于异常数据，可以通过增加或减少数据数目，或转移零误差点，或改变数学模型等方式进行处理；若异常数据虽然存在，但误差在允许的范围内，可不作处理．

3）求解：取直线方程为f（xi）＝a＋bxi，对于式（4）设1≤j，k≤m－1，j≠k，可以通过

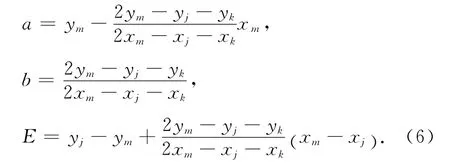
获得参数a，b及逼近值E．取不同的j，k，使最大的E为极小minmaxE＝E＊，从而获得最佳逼近值E＊，此时获得的参数即为最佳参数a＊，b＊．

4 数值分析

2000年1月－2015年6月我国CPI指数来自国家统计局，共186个，每年的数据是12个，归为1组（2015年除外），共有15组数据，先以2003年的数据处理为例．

4．1 实例一

2003年1月到12月的CPI数据有12个，由判断法则进行预处理，用最小二乘法得到的方程用P2003（xi）表示：P2003（xi）＝99．41＋0．26xi，经判断，端点i＝12不是最大误差点，可以运用零误差型极小极大逼近，得到的方程用f2003（xi）表示，其中xi＝1，2，…，12：

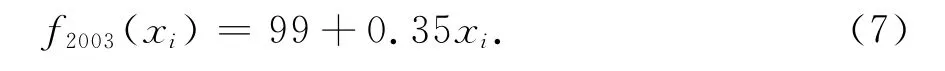
极小化的最大绝对值误差出现在i＝1，9处，为max｜r｜＝1．05，由此构建的2003年CPI通道为：

Channel2003（x）＝f2003（）x±1．05，其中f2003（）x是f2003（xi）在去掉下标“i”后的函数表达，定义区间为［1，12］．将x13＝13代入，得2004年1月CPI指数预测值及波动值：103．55±1．05．已知2014年1月CPI指数是103．2，在预测的范围之内．将预测值与实际值进行比较，预测的误差为0．34%．

文中的图1就是2003年1月至12月的CPI变化，以及CPI通道，在虚线外的点就是2014年1月的CPI指数，图中有关说明可参见前文．

4．2 实例二

如法炮制，按序将2000，2001，…，2014年1月至12月的数据处理结果列于表1．

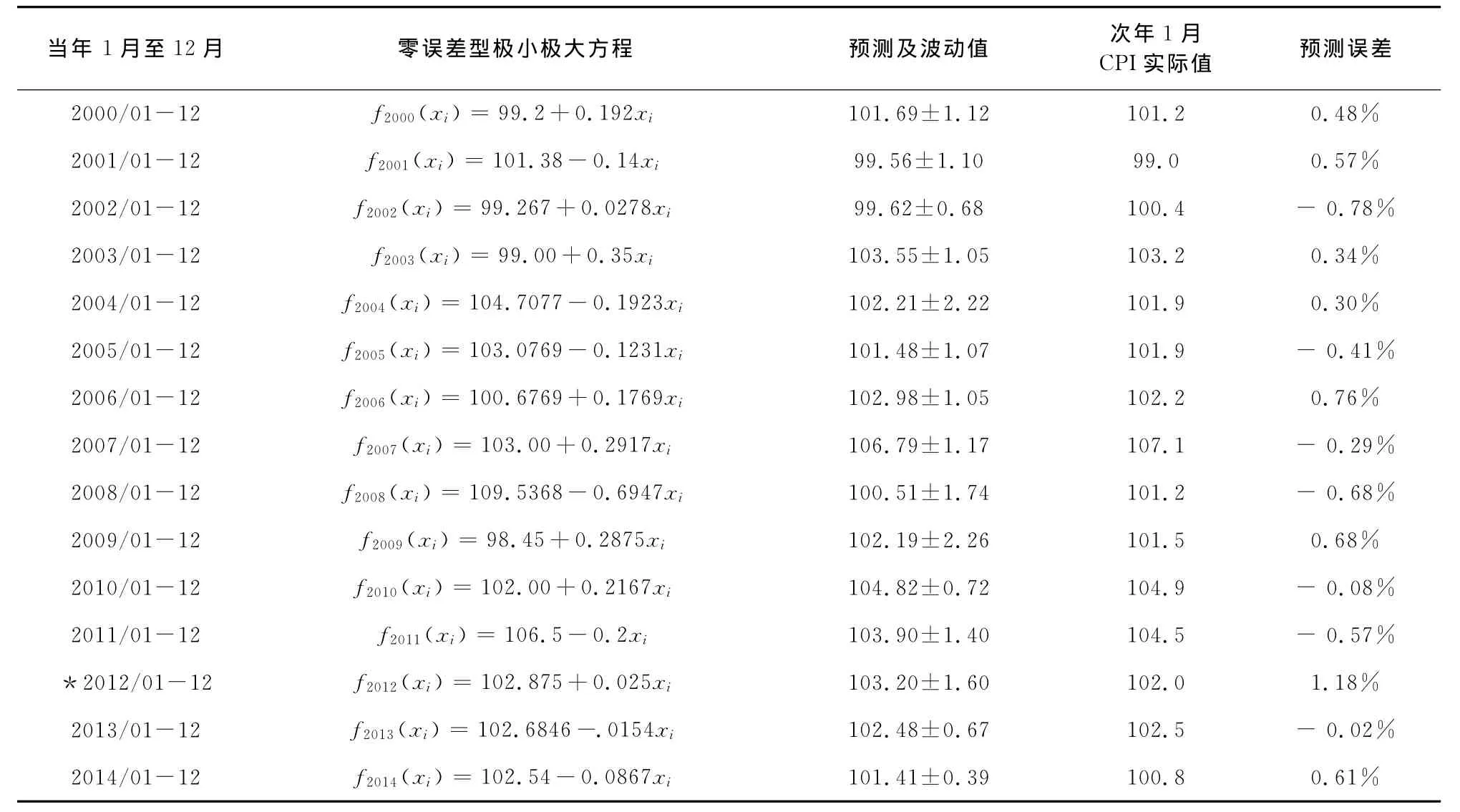
表1 我国2000～2014年，每年1月至12月CPI指数的数据处理及预测

从表1结果看，CPI实际值都落在预测值及波动范围之内，所以预测的结果是有效的．其中2012年带＊的数据属于异常的数据处理，该年11月的CPI指数为102．0，但12月增至104．6，而次年1月又回落到102．0，计算表明12月份的数据属于异常数据，通过零误差点迁移，取绝对值误差最小的点为零误差点，获得表中的方程式．

4．3 实例三

表2是按序2000，2001，…，2014年，当年6月至次年5月的12个CPI数据处理以及对次年6月预测情况，共15组．其中带＊的2013／06－2014／05因出现3个零误差点，故斜率为0，属于特殊方程．为了与表1区别，方程用符号g（xi）表示．

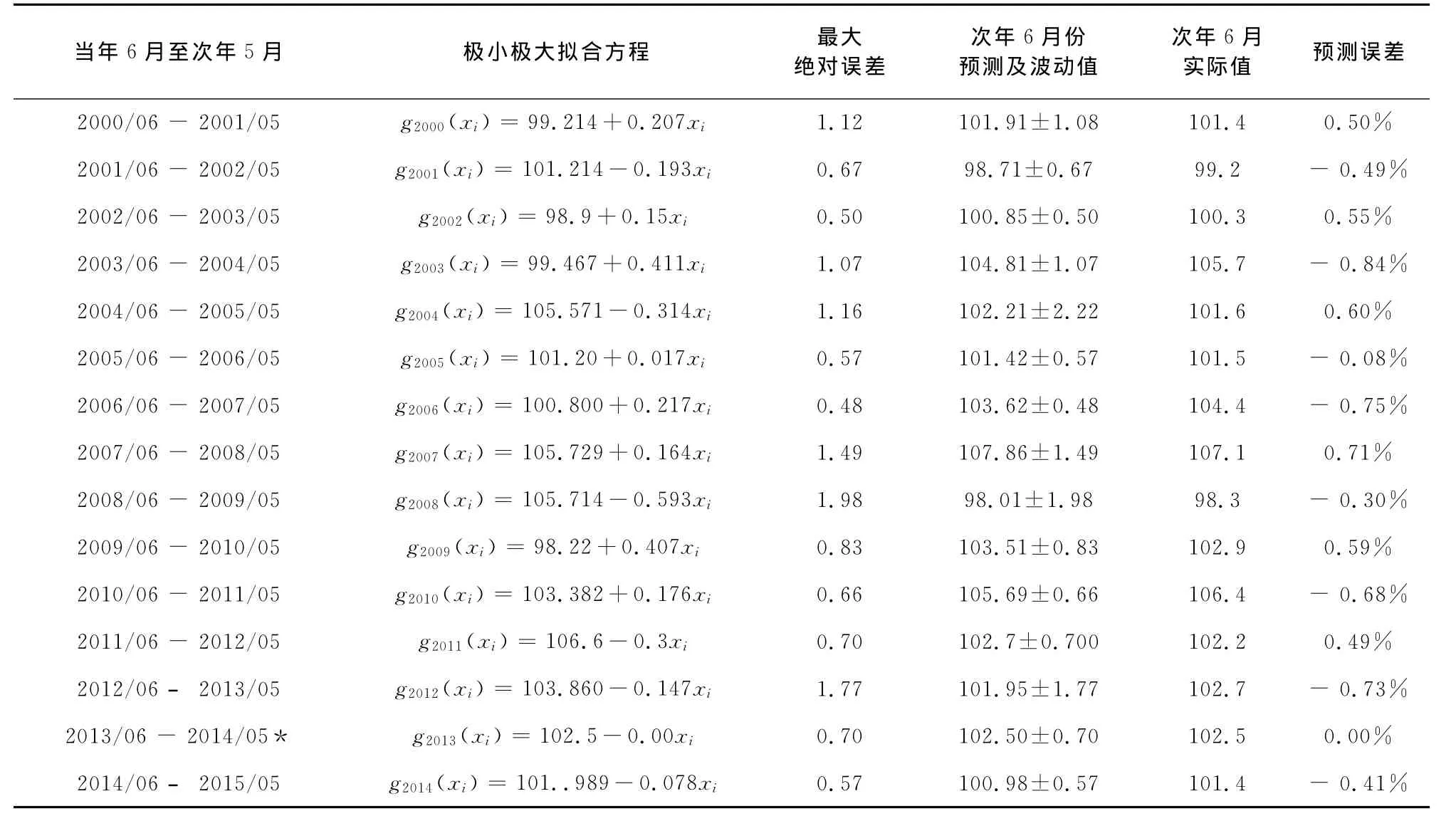
表2 我国2000～2014年，当年6月至次年5月CPI指数的数据处理及预测

5 结 论

提供的通道原理与方法，具有简单易懂、直观性强、计算方便、适用范围广、符合性较好等特点，是曲线拟合的一种推广，目的是使预测及预测误差成为可知与可控．由于直线通道是一个简单的通道，在进一步的探讨中还需要逐步加以完善．

［1］邹正方，黎智，李迪．国际粮价波动对我国CPI影响的实证分析：以玉米、大豆为例［J］．数学的实践与认识，2012，42（17）：41－46．

［2］黄飞雪，金建东．金融危机前后中国房价指数对CPI的影响［J］．经济数学，2010，27（3）：64－72．

［3］陈升，李星野．基于小波分解自回归模型的CPI预测［J］．统计与决策，2012，349（1）：18－20．

［4］李庆华．基于VAR模型的中国消费价格指数分析［J］．华中师范大学学报（人文社会科学版）．2006，45（4）：56－61．

［5］张本丽等．基于ARIMA模型的山东省居民消费价格指数分析［J］．鲁东大学学报，2010，26（3）：285－288．

［6］刘海萍．神经网络在CPI预测中的应用［C］．第五届（2010）中国管理学年会——市场营销分会场论文集，2010．

［7］曾波．居民消费价格指数的 GM（1，1）模型预测［J］．统计与决策，2009，289（13）：7－8．

［8］顾乐民．基于切比雪夫最佳逼近原理的俄罗斯人口变化通道［J］．俄罗斯研究，2015，191（2）：178－192．

［9］Gu LEMIN．Minimax curve fitting method in application of CD production function—— with the grain yield data in China as the example［J］．Journal of Modern Agriculture．2013，2（3）：43－55．

［10］Lemin GU．Zero－Error Type of chebyshev polynomials［J］．International Journal of Modeling and Optimization．2013（3）：272－277．

［11］顾乐民．预测型切比雪夫多项式［J］．计算机工程与应用．2012，48（7）：34－38．