带观察时的跳服从Erlang（n）分布的对偶模型的红利贴现问题＊

谈普林

（武汉大学 数学与统计学院，湖北 武汉 430072）

1 引 言

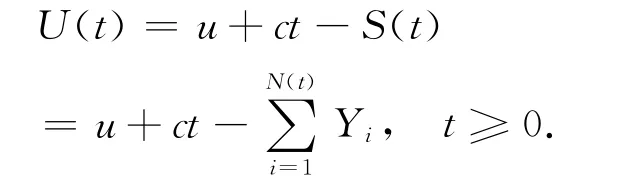
其中，u＝U（0）≥0为初始盈余，c为保费率即收入率，S（t）表示保险公司的总索赔额即支出，一般为复合泊松过程．在研究一般公司的盈余过程时发现公司的支出是持续的，收入是随机的．通过改进得到了对偶风险模型，可参见 Avanzi等人（2007）［1］，Avanzi 和 Gerber （2008）［2］，Gerber 和 Smith（2008）［3］的工作．在对偶风险模型中，t时刻的盈余表示为

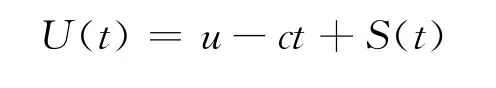
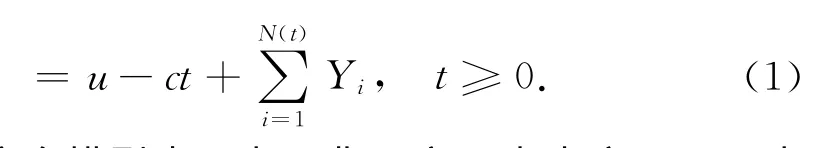
在这个模型中c表示费用率即支出率，S（t）表示总收益，其中N（t）和Yi相互独立．假设是非负的独立同分布随机序列，密度函数为p（y）且期望为μ＝E（Y1）．

De Finetti（1957）［4］首次提出在风险模型中考虑分红策略，认为这个过程更贴切实际情形．分红策略一般有两种．一种是边值策略，即当盈余过程超过给定的边值时，红利才分发且发放超过边值部分的全部．另一种是阀值策略，相同的是在盈余过程超过给定阀值才分发红利，不同的是当超过阀值时，分红率是一个固定的常数．Avanzi等人（2007）［1］研究了在边值策略下对偶风险模型的最优红利问题，Avanzi等人（2013）［5］研究了在边值策略下带观察时的对偶风险模型的破产概率和贴现红利，Ng（2009）［6］研究了在阀值策略下对偶风险模型的贴现红利．关于收益过程，这些文章都是基于复合泊松过程讨论的，在模型的进一步推广时，收益改用更新过程来研究．Li和 Garrido（2004）［7］研究了复合更新过程（索赔时间间隔即跳过程服从Erlang（n）分布）下风险模型的破产概率，Albrecher等人（2005）［8］则给出了跳服从广义Erlang（n）分布的贴现红利任意阶矩，Eugenio等人（2014）［9］在跳服从Erlang（n）分布下把模型推广到对偶情形并讨论破产概率和贴现红利问题，Yang和Sendova（2014）［10］在此基础上推广到广义Erlang（n）分布．关于收益过程采用复合更新过程来描述已经有很多文章了，但是他们都没考虑带观察时的情形．基于此，考虑在边值策略下带观察时跳服从Erlang（n）分布的对偶风险模型．不同于Peng等人（2013）［11］（红利分发和破产均在观察时发生）的研究，而是类似于Avanzi等人（2013）［5］红利分发只在观察时发生而破产可能是在任意时刻发生的（即盈余U（t）＜0就破产）．

本文的结构如下：在第二部分，介绍具体模型和定义．在第三部分第一节，给出红利期望贴现函数V（u；b）满足的微积分方程组．在第三部分第二节，利用第三部分第一节结果讨论收益额服从PH（m）分布时的红利期望贴现函数，并给出V（u；b）的解析解．在第三部分第三节，给出观察时及收益额均服从指数分布时V（u；b）的具体求解．在第四部分第一节，给出跳退化为指数分布时V（u；b）的显示解及其极限，并与 Avanzi等人（2007）［1］和 Avanzi等人（2013）［5］的结果进行比较．在第四部分第二节，给出跳服从Erlang（2）分布时，V（u；b）的数值举例．

2 模型及定义

根据式（1），｛U（t），t≥0｝ 的破产时间定义为τ＝inf ｛t≥0：U（t）≤0｝ ．计 数 过 程N（t）＝min ｛k：T1＋T2＋…＋Tk＋1＞t｝是 一 个 更 新 过程，是正的独立同分布随机序列（T定义i为第（i－1）次产生收益到第i次产生收益的时间间隔）．

假定Ti（i＝1，2，…）服从 Erlang（n）分布，即密度函数为！．假设公司是可盈利的，即c＜μ／E（Ti）⇔cn＜λμ．

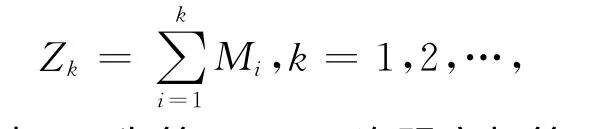
其中Mi为第（i－1）次观察与第i次观察所经历的时间，｛Mi，i≥1｝独立同分布且分布函数为F（x），并假设与 ｛Yi，i≥1｝以及相互独立．进一步，假设边值策略下红利分发只发生在时刻，即任意时刻Zk盈余超出边界值b（＞0），则超出部分全部作为红利分发．

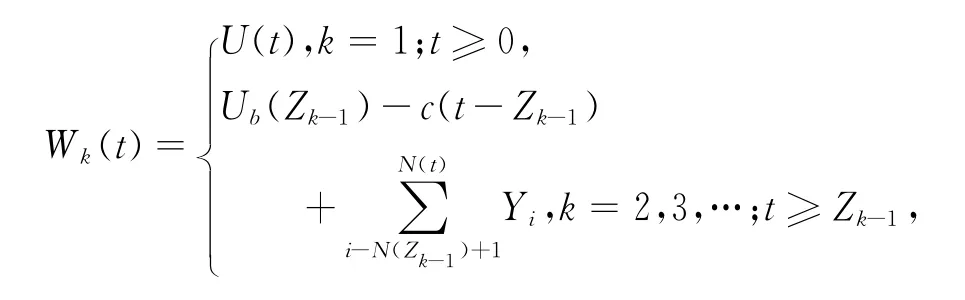
以及对k＝1，2…，

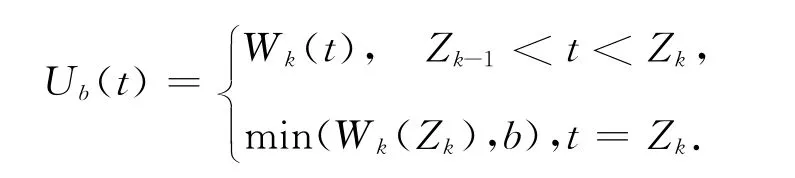
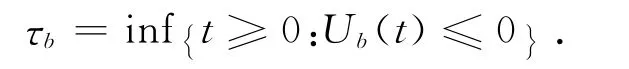
类似地定义当前模型的破产时间为令Kb＝则Kb表示直到破产为止总共发生观察的次数．

红利期望贴现函数可定义为

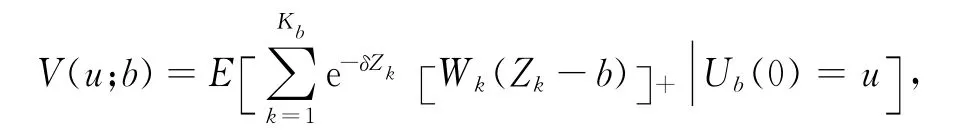
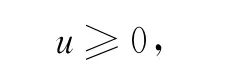
其中a＋＝max（a，0），δ为贴现力．假设V（u；b）线性有界．图1给出了盈余过程的变化轨迹图．

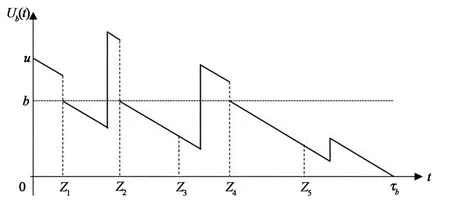
图1 盈余过程 ｛Ub（t），t≥0｝ 的变化轨迹图

3 跳服从Erlang（n）分布时V（u，b）的求解

由Erlang（n）是n个独立同分布的指数分布之和，把跳过程分成n步，前n－1步跳的大小为0，最后一步跳的密度函数为p（y），y≥0．第i步跳的红利期望贴现函数记为Vi（u；b），i＝1，2，…，n，且假设在b点连续．对i＝1，2，…，n，定义

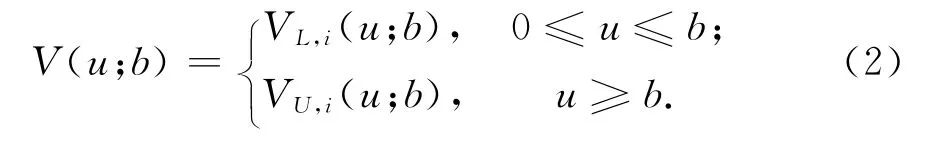
3．1 V（u；b）的微积分方程组

定理1Vi（u；b），i＝1，2…，n，满足下面的微积分方程组

当i＝1，2，…，n－1时，

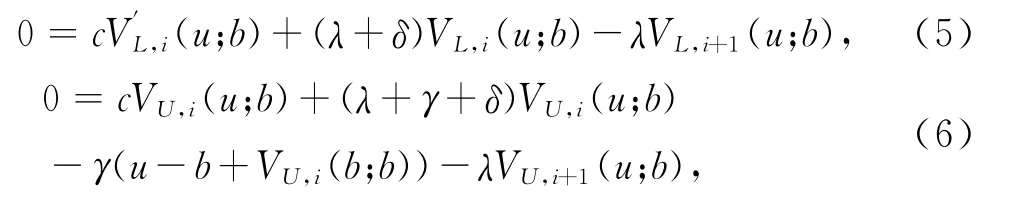
当i＝n时，

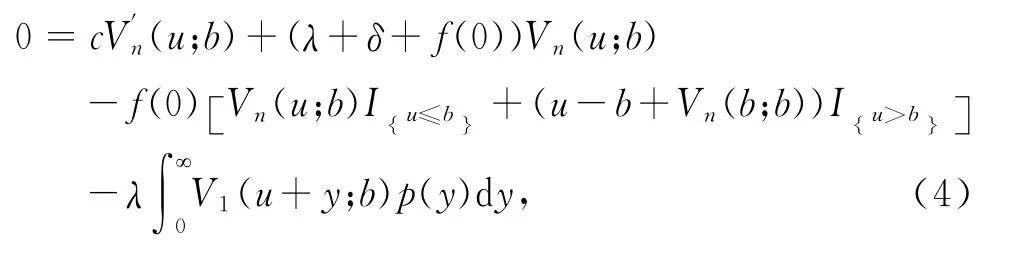
Vi（u；b），i＝1，2，…，n满足边界条件

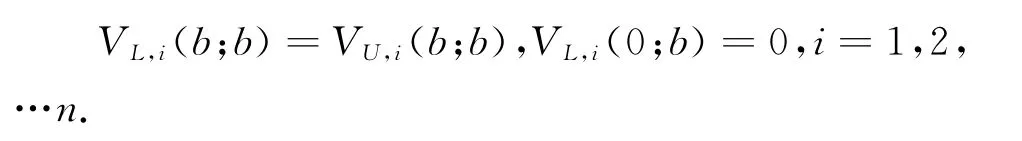
其中f（x）是观察时分布函数F（x）的密度函数．

证明 对u≥0，在每一步i足够小的时间区间［0，h］中考虑跳和观察两个事件，注意到这两个事件是相互独立的，在这个区间中根据它们是否发生以及发生的先后关系得到下面的等式．

当i＝1，2，…n－1时，跳的大小为0，于是

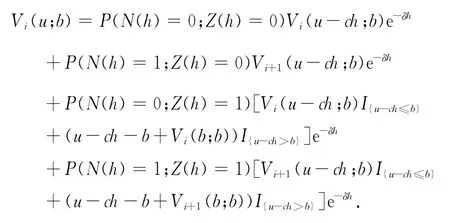
对上式代入密度函数f（x），利用泰勒展式得到

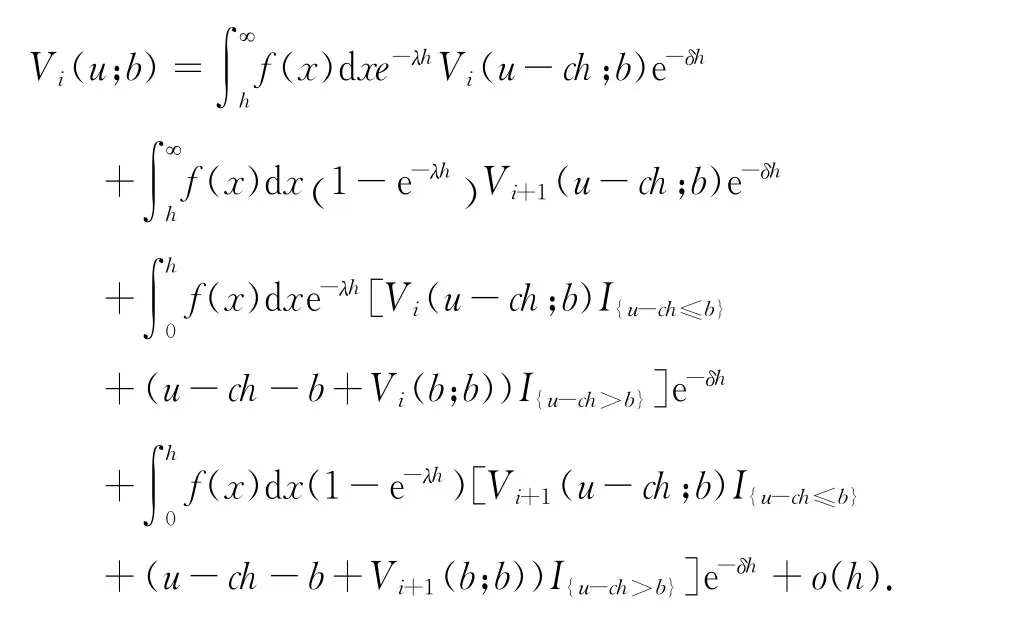
可以看出上面等式右边第四项趋向于o（h2）．于是，对上式两边同时除以h，并令h→0即可得式（2）．

当i＝n时，跳的大小（即收益额）的密度函数为p（y），y≥0，类似可推得

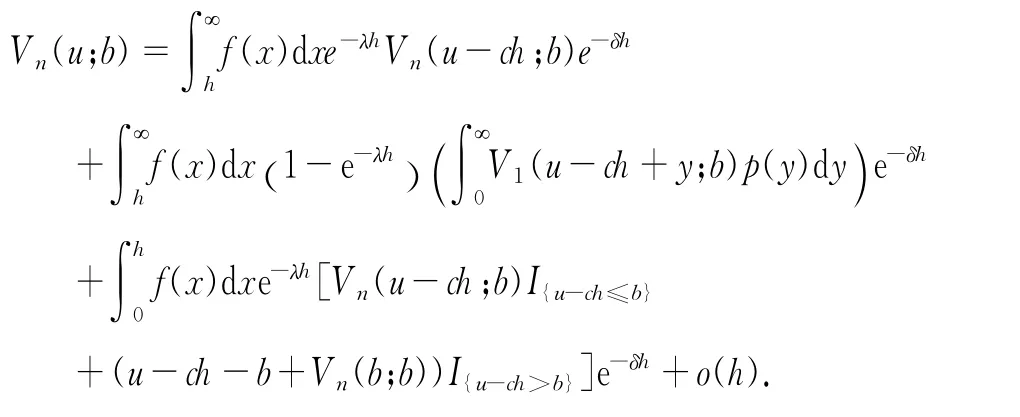
由上式同理可证式（3）成立，边界条件由初始值假设和连续性假设得到．

当f（x）＝，x＞0时，由定理1可以得到下面的推论．

推论1Vi（u；b），i＝1，2，…，n满足下面的微积分方程组

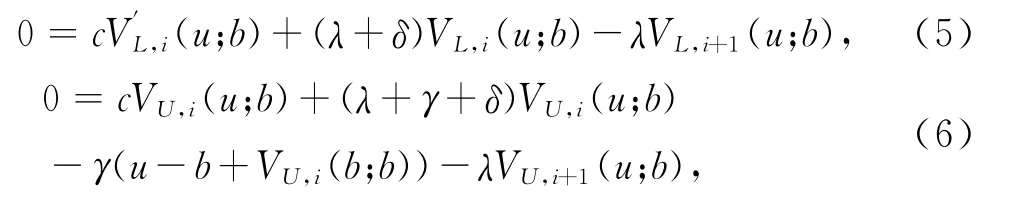
当i＝n时，

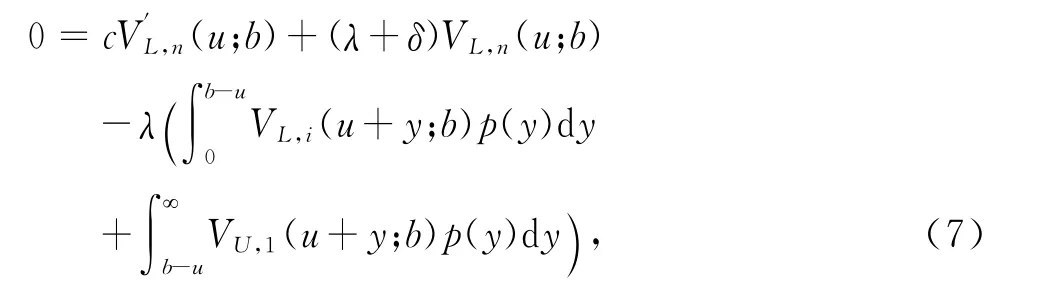
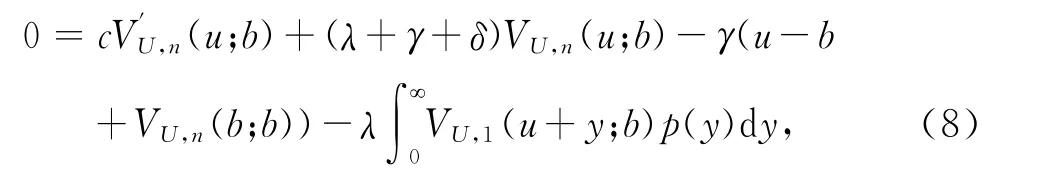
Vi（u；b），i＝1，2，…n满足边界条件

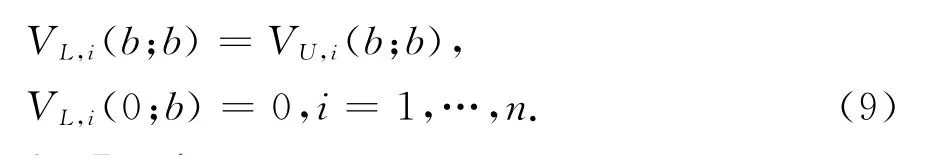
证明 由于f（0）＝γ，并把式（2）代入定理1即可证明推论成立．

注1 在推论1中，i＝n时发生了跳，由连续性假设可知令u＝b，有（b；b）＝（b；b），该条件在后面求解V（u；b）时将被应用．

注2 显然V（u；b）≡V1（u；b），因此只需求解（u；b）和VL，1（u；b）．

3．2 观察时和收益额分别服从指数和PH（m）

分布时V（u；b）的求解

假定Erlang（2）为PH（m）分布，其中PH（m）定义可参见 Eugenio等人（2014）［9］的5．2部分．

3．2．1VU，1（u；b）的解析解

由Eugenio等人（2014）［9］的定理5．2知p（xu）的零化因子为qΒ（－Du），其中Du＝∂／∂u，qΒ（y）＝Det（Β－yΙm）．考虑qΒ（－Du）的多项式形式：

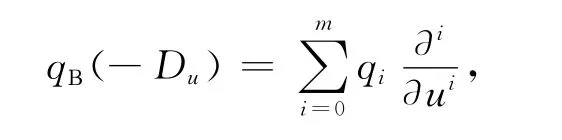
其中qi，i＝0，1，…，m，是常数．

对式（8）做变换y＋u＝x得到

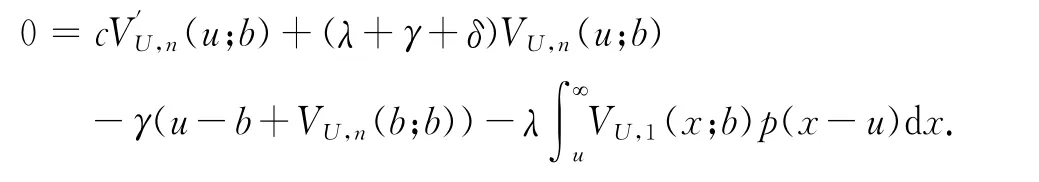
对上式作用qΒ（－Du）＝得到

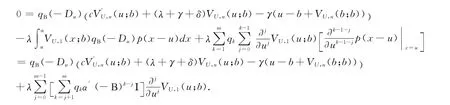
对上式求偏导∂／∂u得到

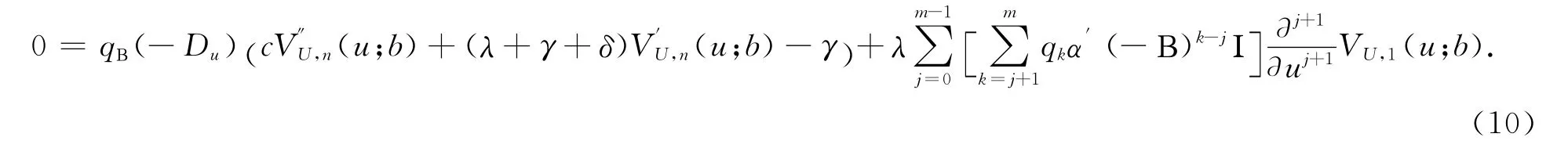
对 式（6）求偏导∂／∂u，当i＝1，2，…，n－1时有

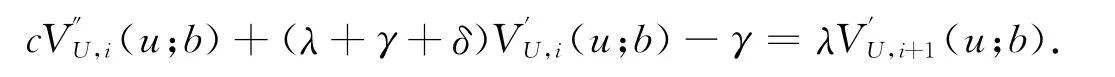
上式为递归形式，令∂／∂u＝Du，可知

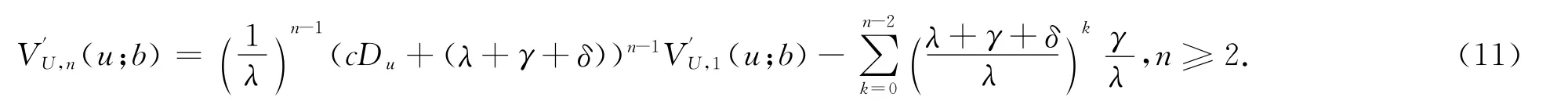
把式（11）代入式（10）式整理可得

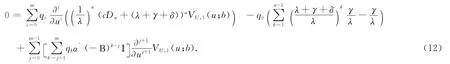
上式也可以归纳为

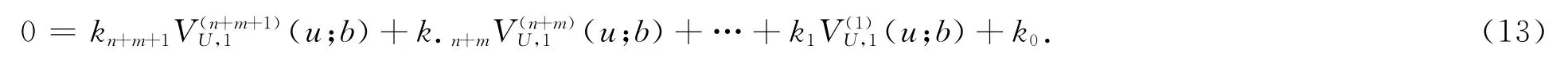
故VU，1（u；b）的解析解为

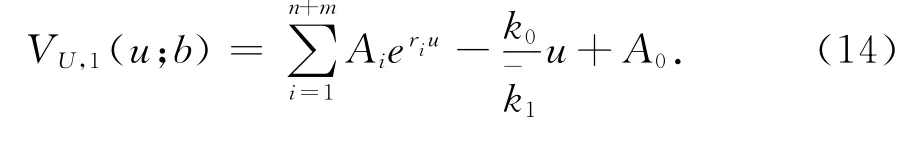
3．2．2VL，1（u；b）的解析解

由式 （5）可得，

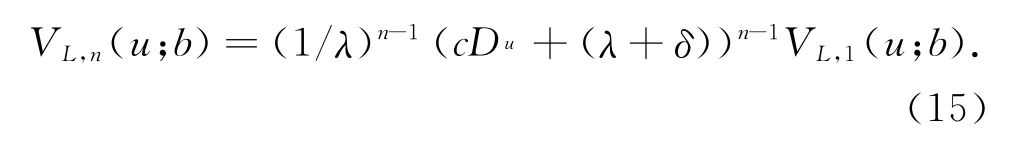
先对式（7）做变换y＋u＝x，再作用qΒ（－Du）得到

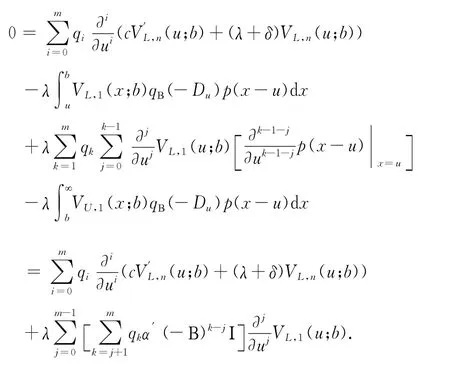
将式（15）代入上式整理可得到

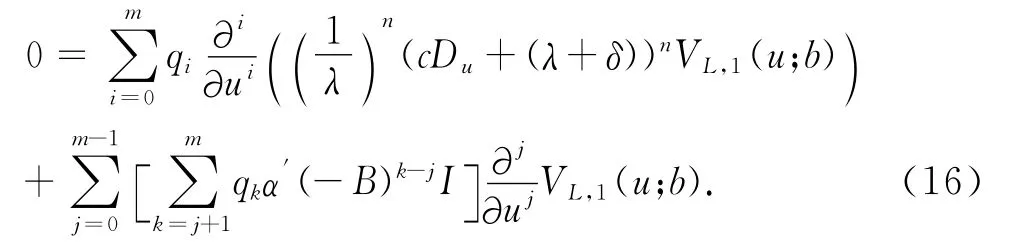
注意到对照Eugenio等人（2014）［9］的 （5．7）式，发现与上式是相同的．因此得到VL，1（u；b）的解析解为

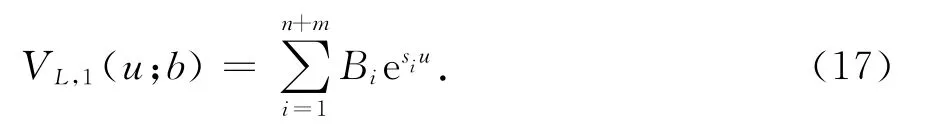
3．3 观察时及收益额均服从指数分布时V（u；b）的求解

在PH（m）中令m＝1，即p（y）＝βe－βy，y＞0，为指数分布，探讨VU，1（u；b）和VL，1（u；b）显示解的具体求解过程．

3．3．1VU，1（u；b）的解析解

由于此时p（y）为指数分布，整理式（12）得到

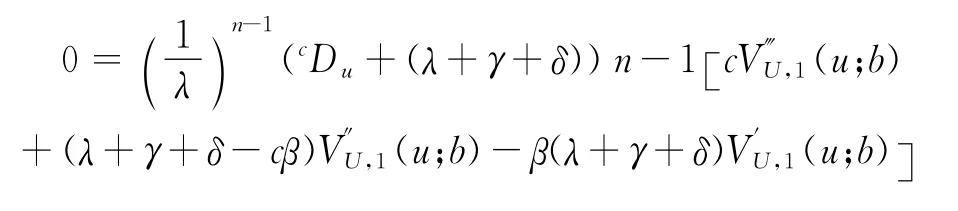
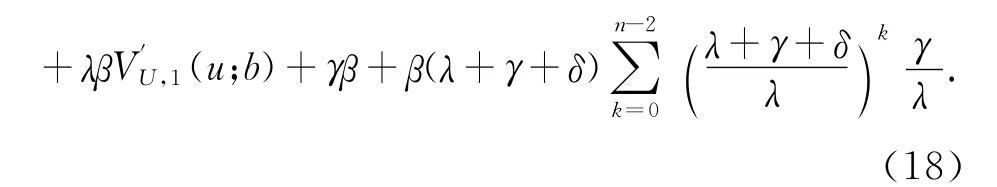
上式经过展开可以得到关于VU，1（u；b）的n＋2次微分方程，即

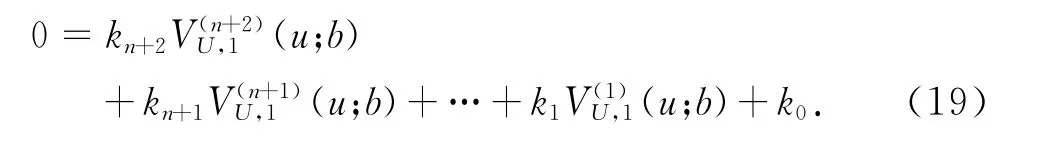
其中k0，k1，…，kn＋2是由λ，γ，δ，β，c组成的常数．令

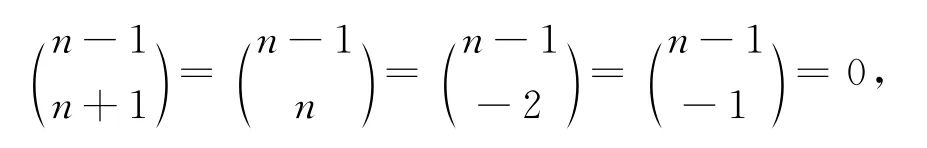
则当i＝1，2，…，n＋2时，

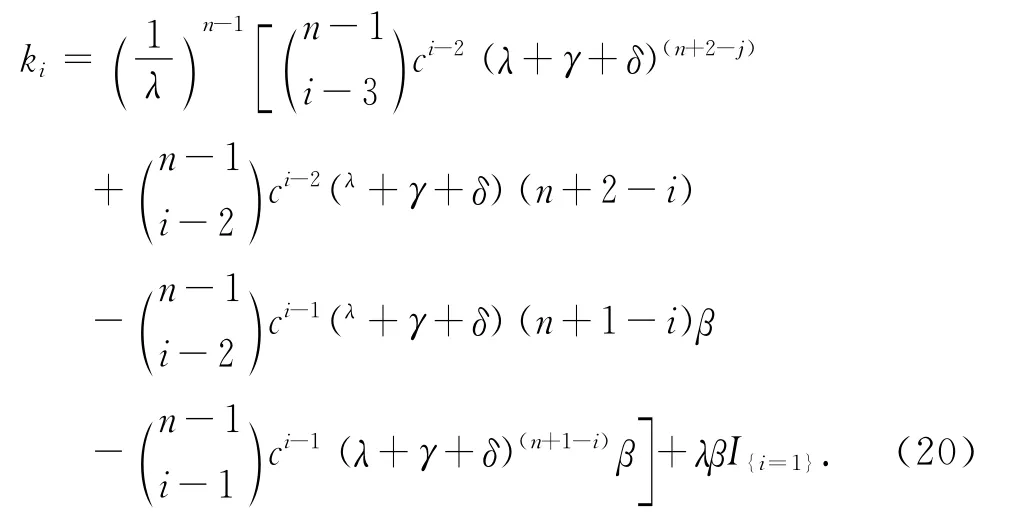
当i＝0时

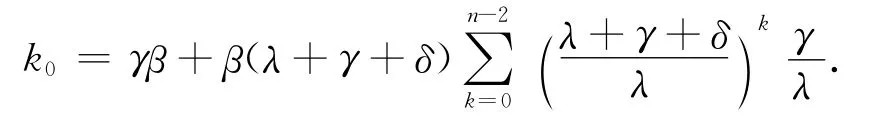
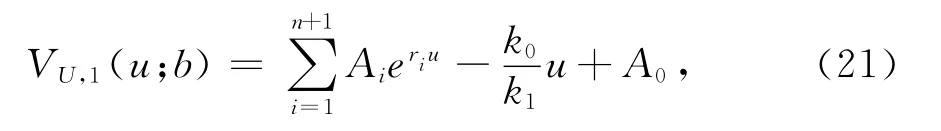
其中Ai为待求系数，ri为下面式（22）的根，

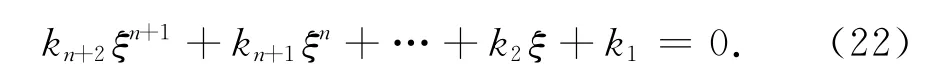
引理1 方程式（22）有n个实部为负的根，且有唯一的正根．

证明 首先令f（ξ）＝＋…＋下面计算f（ξ），由式（20）可得

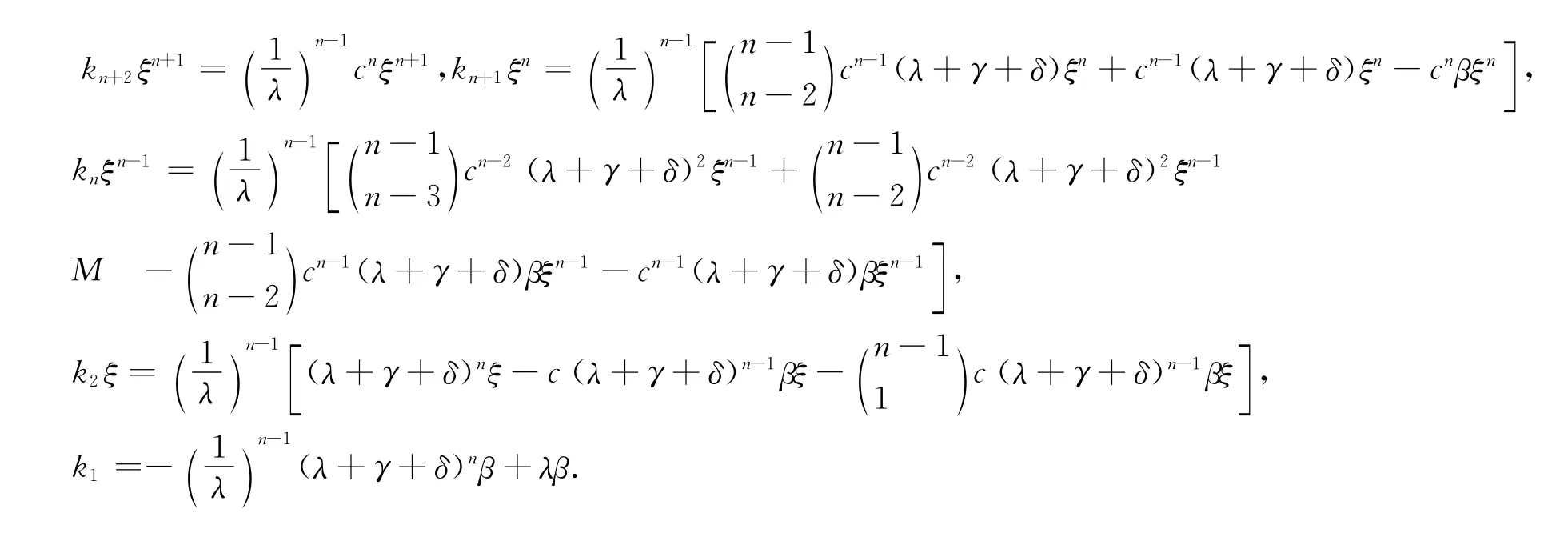
注意到上面系列等式左边相加等于f（ξ），右边相邻两式正负依次组合在一起提取公共项（1／λ）n－1（ξ－β）然后相加即得二项式展开形式．

经过整理可得

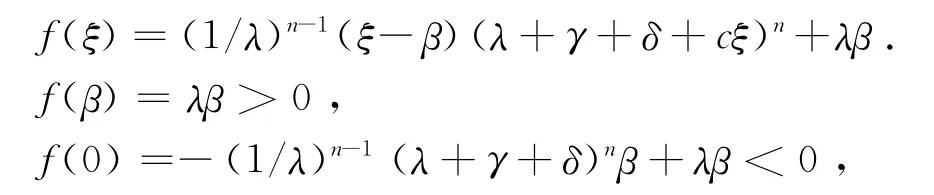
故存在一个正根．

令f（－ξ）＝0，整理后得到

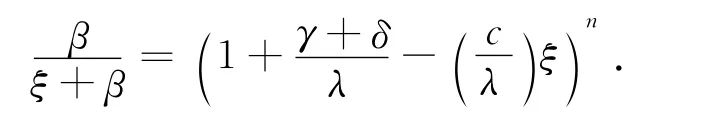
因为参数为β的指数分布的拉普拉斯变换等于，所以有的拉普拉斯变换）．根据Eugenio等人（2014）［9］第三部分的讨论，可知方程22有n个实部为负的根．又因为方程22共有n＋1个根，故有唯一的正根．

由引理1，假设是唯一的正根，根据V（u；b）线性有界假设，可得＝0．对VU，1（u；b）还有A0，A1，．．．，An共n＋1个待求系数，将在后文给出具体的求解过程．

3．3．2VL，1（u；b）的解析解

整理 式（16）得到

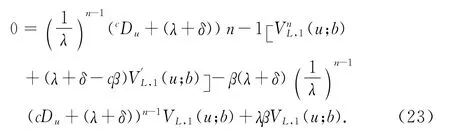
把 式（23）改写成式 （24）

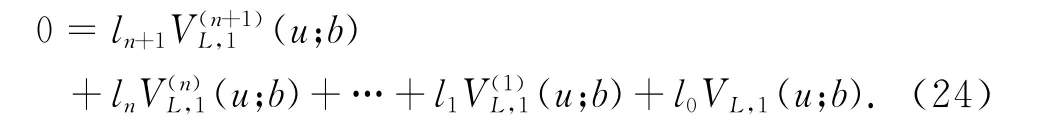
其中l1，i＝0，1，…，n＋1，可写成下面形式

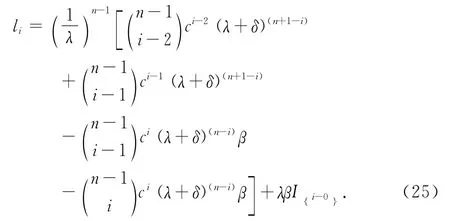
于是，VL，1（u；b）的形式解为

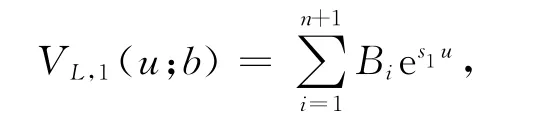
其中，i＝1，2，…，n＋1，是下面方程的根

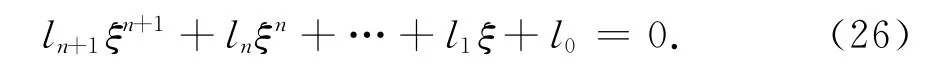
注意到有A0，A1，…，An，B1，B2，…，Bn＋1共2n＋2个待求系数，需要2n＋2个方程．首先，根据推论1的边界条件共得到2n个方程．其次，利用注1得到一个方程．最后，把VU，1（u；b）和VL，1（u；b）的解析解以及 式（15）代入 式（7），根据的系数等于零得到第2n＋2个方程．

4 红利期望贴现函数V（u；b）的求解实例

现在讨论观察时及收益额均服从指数分布时V（u；b）的显示解和数值举例．其中，在4．1中考虑跳服从指数分布时V（u；b）的显示解以及γ→ ∞时V（u；b）的极限．在4．2中考虑跳服从 Erlang（2）分布，并给出相应的数值举例．在不引起歧义的情况下，令V1（u；b）＝VL，1（u；b），

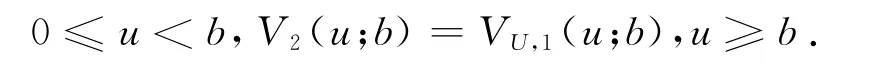
4．1 跳及观察时均服从指数分布时V（u；b）的求解

假设跳服从Erlang（1）分布，即指数分布，则式（7）改写为

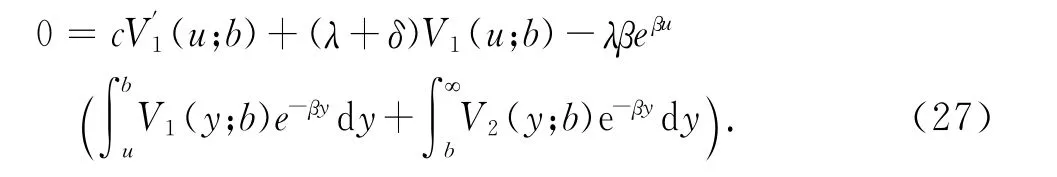
根据 式（21）得

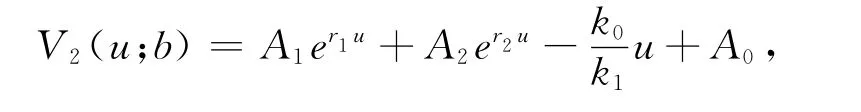
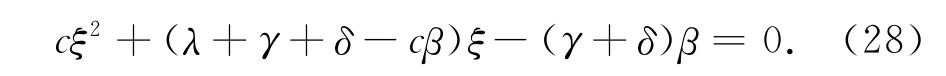
由线性有界假设知A2＝0，因此

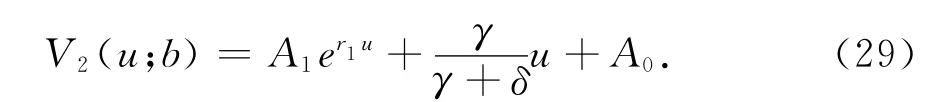
同理可得V1（u；b）的解析解为

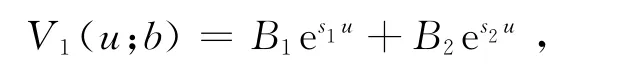
其中，s1，s2是下面方程的两根

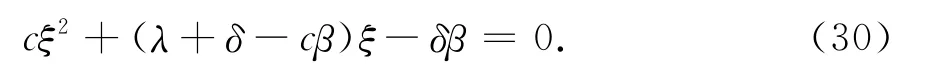
根据V1（0；b）＝0，可推得

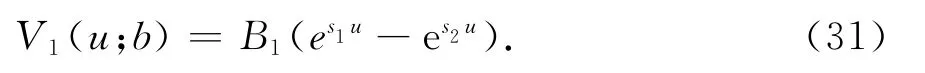
由边界条件V1（b；b）＝V2（b；b）和（b；b）＝（b；b）以及 式（29）和（31）得

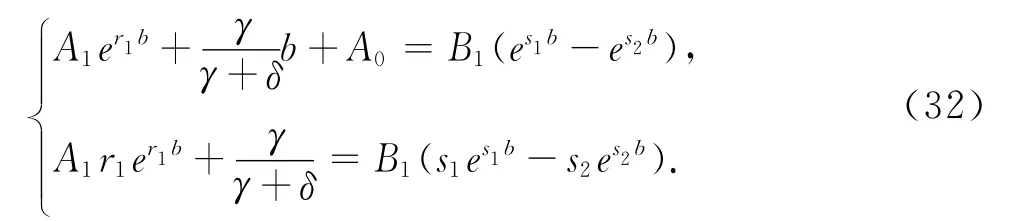
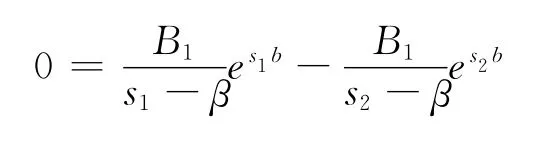
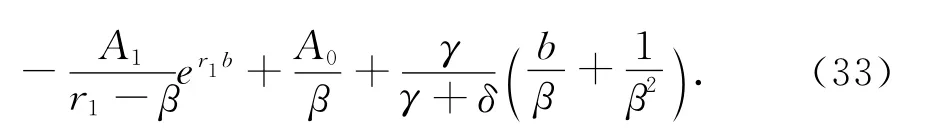
于是，由 式（32）和式（33）求得V1（u；b），V2（u；b）

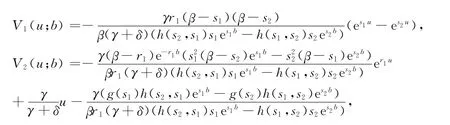
其中g（x）＝βbr1x＋r1x－β（r1＋x），h（x，y）＝（β－x）（y－r1）．

注3 将上述结果与 Avanzi等人（2013）［5］的（4．2）式对比，当－ργ＋δ＝r1时，由r1和s1分别是方程（28）和 （30）的根，可得下面的等式

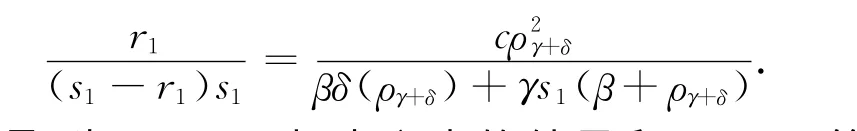
于是，当n＝1时，本文中的结果和Avanzi等人（2013）［5］的（4．2）式是一致的．

注4 由求解r对应的方程可得出＝－11．对V1（u；b），0＜u≤b，取极限得到

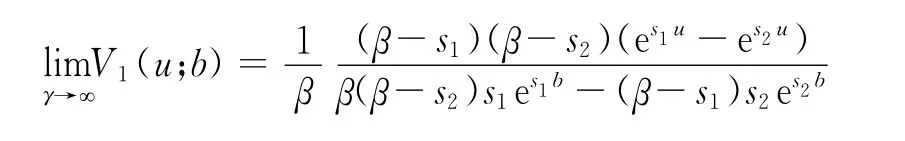
分别为

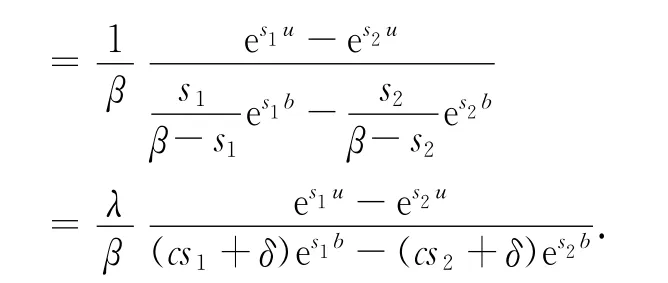
对上述结论做数值模拟，见图2、图3和表1、表2．其中，图2和图3分别表示固定b在不同u值下随着γ趋向无穷V1（u；b）的极限值．对比表1和表2会发现相同u值下，V1（u；b）随b的增大而减小．

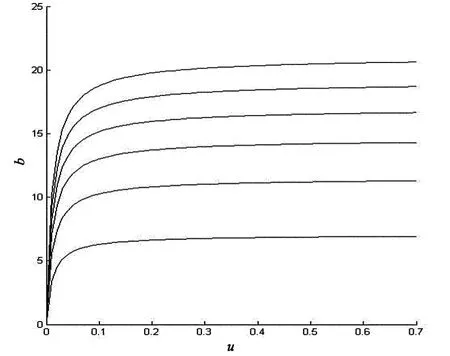
图2 c＝0．8，λ＝1，δ＝0．01，β＝1，b＝12

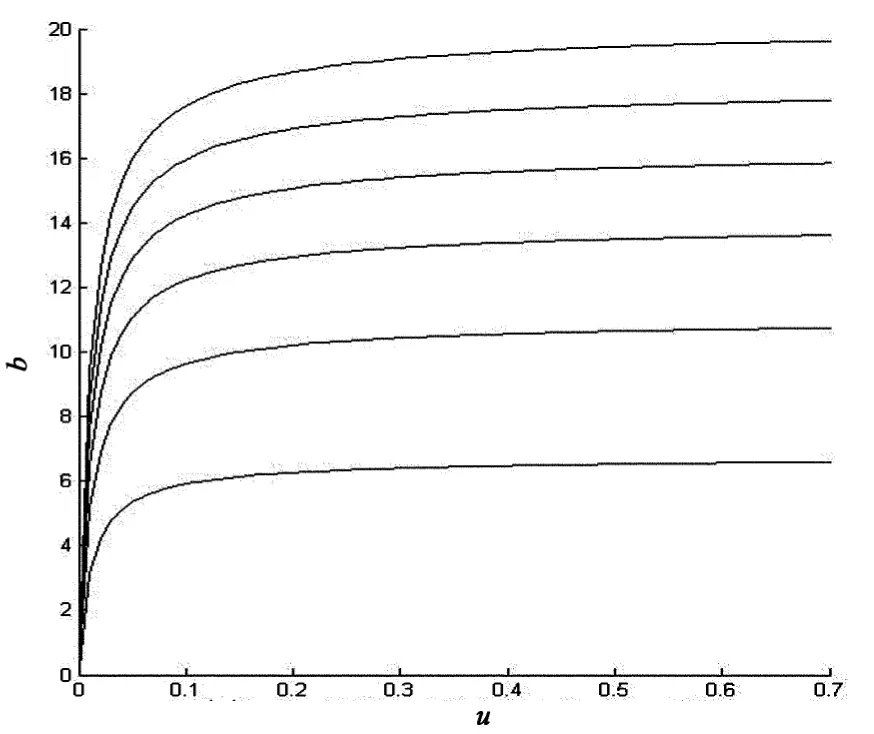
图3 c＝0．8，λ＝1，δ＝0．01，β＝1，b＝14

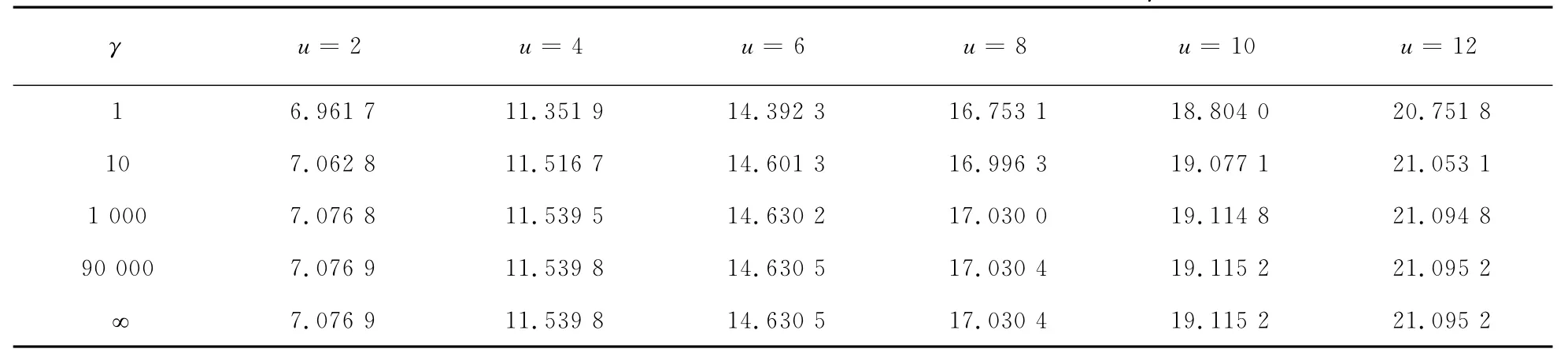
表1 参数γ和u对V1（u；γ）的影响，其中c＝0．8，λ＝1，δ＝0．01，β＝1，b＝12

表2 参数γ和u对V1（u；γ）的影响，其中c＝0．8，λ＝1，δ＝0．01，β＝1，b＝14

4．2 跳和观察时分别服从Erlang（2）和指数分布时V（u；b）的数值举例

跳服从Erlang（2）分布时，由第三部分第三节的讨论可知

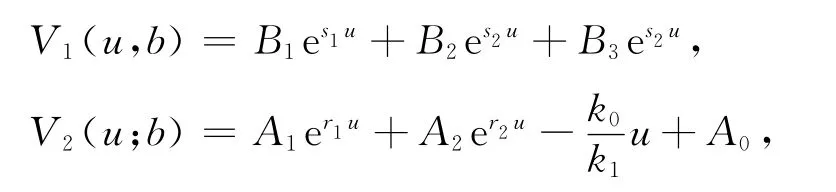
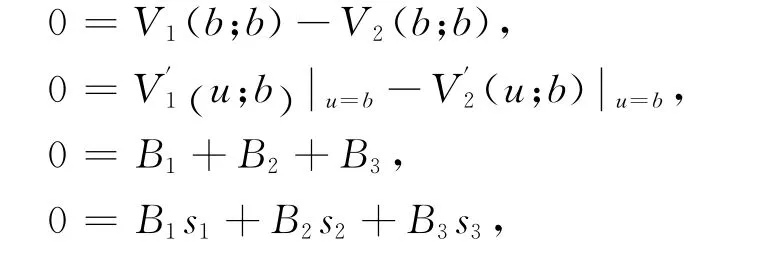
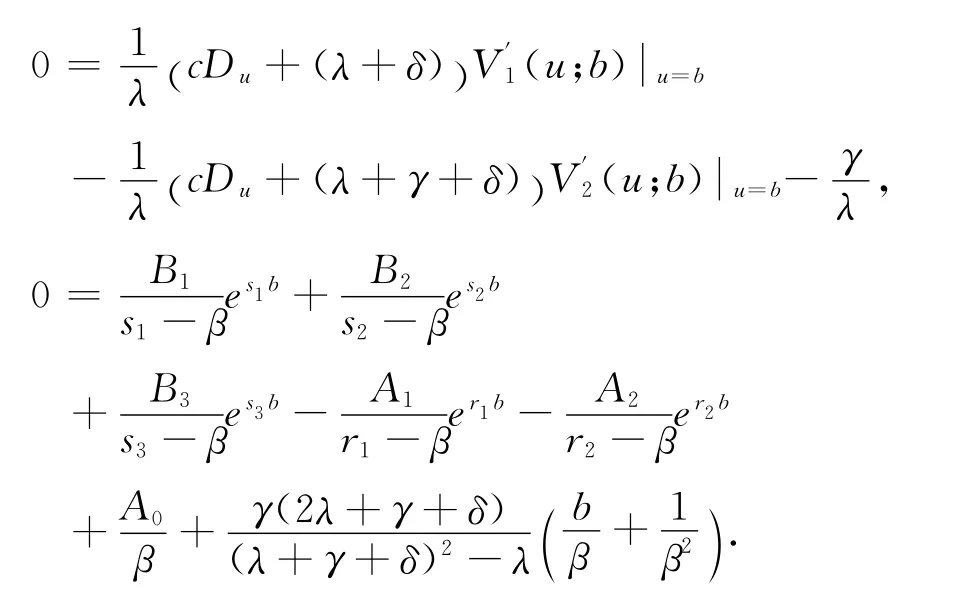
例 令c＝0．8，λ＝2，δ＝0．05，β＝1求得根s1＝0．1515，s2＝－0．5625，s3＝－3．7140和r1＝－3．9374，r2＝－6．0069．由上面的方程组可以看出待求系数与b相关，即给定b的值就可以求出相应的系数，故有

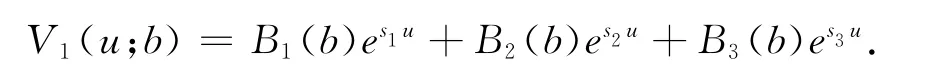
经过数值计算得到图4和表3，图表中的数据说明总体上V1（u；b）随着b的增大而减小，随着u的增大而增大．

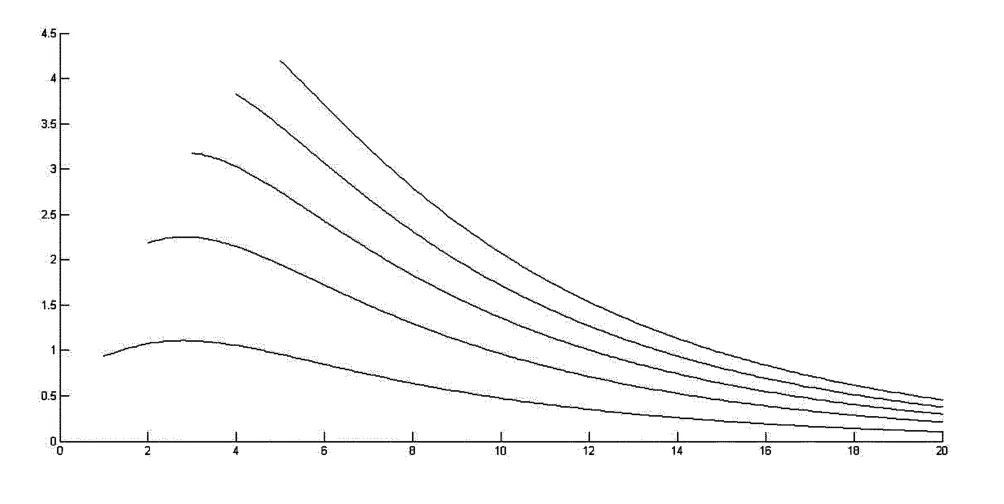
图4 关于b，V1（u；b）的函数图像，u＝1，2，…，5

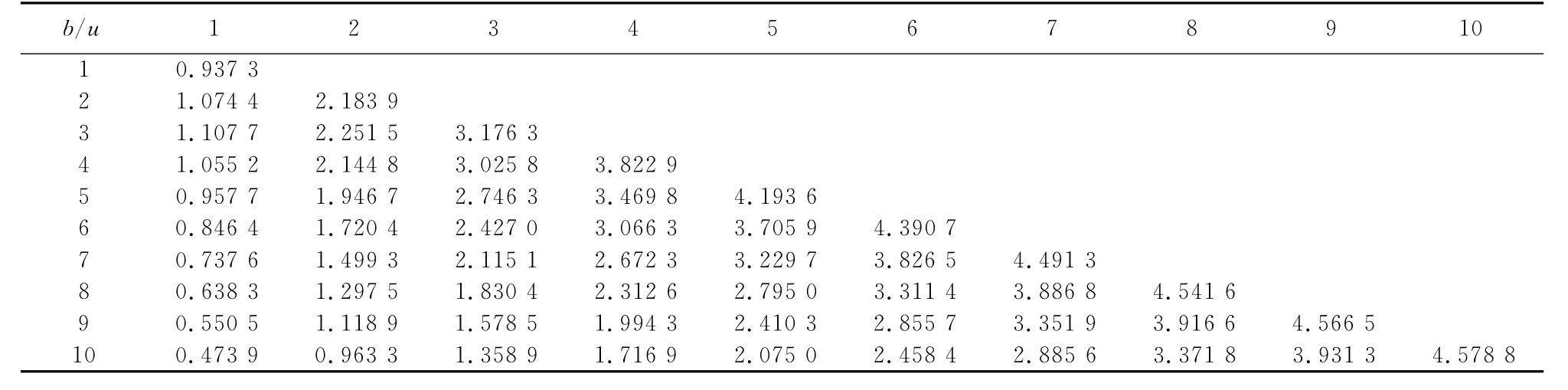
表4 参数γ和u对V1（u；γ）的影响，其中c＝0．8，λ＝2，γ＝2，δ＝0．05，β＝1

5 结 论

建立了边值策略下带观察时的跳服从Erlang（n）分布的对偶风险模型，通过求解随机微分方程组给出了红利期望贴现函数V（u；b）的解析解．相比较于传统的风险模型用于研究保险公司的盈余过程，而其对偶模型适用于一般公司．对比Eugenio等人（2014）［9］研究Erlang（n）分布，利用更新过程的无记忆性，把Erlang（n）分布分成n个阶段来讨论．红利分发只在观察时发生的假设和使用更一般的更新过程来研究使研究结果更加具有现实意义和一般性．对于观察时为指数分布等其它情形，可以进一步使用其他分布来研究．

［1］B AVANZI，H U GERBER，E S W SHIU．Optimal dividends in the dual model［J］．Insurance：Mathematics and Economics，2007，41（1）：111－123．

［2］B AVANZI，H U GERBER．Optimal dividends in the dual model with diffusion［J］．ASTIN Bulletin，2008，38（2）：653－667．

［3］H U GERBER，N SMITH．Optimal dividends with incomplete information in the dual model［J］．Insurance：Mathemat－ics and Economics，2008，43（2）：227－233．

［4］B DE FINETTI．Su un＇impostazione alternatival dell teoria colletiva del rischio［C］．／／Proceedings of the Transactions of the XV International Congress of Actuaries，1957，2（2）：433－443．

［5］B AVANZI，E C K CHEUNG，B WONG，etal．On a periodic dividend barrier strategy in the dual model with continuous monitoring of solvency［J］．Insurance：Mathematics and Economics，2013，52（1）：98－113．

［6］A C NG．On a dual model with a dividend threshold［J］．Insurance：Mathematics and Economics，2009，44（2）：315－324．

［7］SM LI，J GARRIDO．On ruin for the Erlang（n）risk process［J］．Insurance：Mathematics and Economics，2004，34（3）：391－408．

［8］H ALBRECHER，M M CLARAMUNT，M MARMOL．On the distribution of dividend payments in a Sparre Andersen model with generalized Erlang（n）interclaim times［J］．Insurance：Mathematics and Economics，2005，37（2）：324－334．

［9］V R EUGENIO，M R C RUI，D E ALFREDO．Some advances on the Erlang（n）dual risk model［J］．ASTIN Bulletin，2014，45（1）：127－150．

［10］C YANG，K P SENDOVA．The ruin time under the Sparre－Andersen dual model［J］．Insurance：Mathematics and Economics，2014，54（1）：28－40．

［11］D PENG，D H LIU，Z M LIU．Dividend problems in the dual risk model with exponentially distributed observation time［J］．Statistics and Probability Letters，2013，83（3）：841－849．