线圈和模具结构对板材电磁脉冲成形效率的影响
朱月亭,莫健华,崔晓辉,范 伟,周 波
(华中科技大学 材料成形与模具技术国家重点实验室,湖北 武汉430074)
0 前言
电磁成形是一种利用脉冲磁场力对工件进行高速加工的方法[1]。研究表明[2][3]:材料在高速变形条件下会出现晶体孪生、组织相变、绝热剪切等动力学行为。这些动力学行为使电磁成形获得高于传统冲压加工下的成形性能。并且电磁成形非常适合于难变形、高电导率的轻合金材料,比如铝合金、镁合金。因此,电磁成形成为未来轻量化制造业的关键技术之一。但有研究表明,电磁脉冲成形技术很难直接制造大尺寸、复杂零件[4]。其中一个重要原因是电容器存储的电能大部分以磁场泄露和热能方式损耗,最终只有很小一部分被转化成工件的塑性变形能,使能量利用率很低。例如,板材电磁成形的能量利用率小于5%、管件的则小于25%[5]。因此,如何提高电磁成形的能量利用效率成为学者们的研究热点。
电磁成形能量利用效率方面,国内外学者们的研究成果主要集中在两个方面:①电流频率。比如Yu 等[6]采用顺序耦合法研究了电流频率对管件电磁缩径成形的影响,发现存在一个特殊的频率范围时管件的变形量接近于最佳频率对应的最大值。在这个特殊频率范围内管件塑性变形最大,相应的趋肤深度在0.61~0.7 之间。初红艳等[7]得出一种普遍认识,即当趋肤深度小于或等于板材厚度时,设备能力利用率最高。Zhang 等[8]通过模拟和实验研究了不同工作条件对电磁胀形管件轮廓和成形效率的影响,发现当趋肤深度为0.9mm 时(管件壁厚为1mm),电磁成形的能量利用率最大,当趋肤深度大于1mm时,成形效率急剧下降。这是因为,当趋肤深度大于管件厚度时,电磁线从管件渗出加剧,放电能量不能有效地用来成形管件。肖师杰等[9]运用有限元分析对多组频率下成形高度与塑性应变能进行对比,得到实验中最佳频率3487Hz(电容为700μF),塑性应变能达到最大值45J,能量利用率为6.25%,得到最佳放电频率能提高电磁成形能量利用率的结论。②线圈结构和尺寸。于海平[10]等研究了不同线圈长度对管件变形量和能量利用率的影响,发现在相同放电能量下,线圈尺寸越长,管件成形能量利用率越低。日本电器通信大学的Suzuki[11]通过调整放电电压和集磁器的结构保护线圈并提高其成形效率。陈忠[12]等通过改变线圈的结构,控制磁压力分布,进而控制毛坯的变形分布。
从上面的研究可知,线圈结构对电磁成形的影响主要集中在管件成形方面。与管件成形相比,线圈结构形状和与线圈相对应的凹模结构均会对板材的电磁成形有很大影响。但这些文献都没有提及模具尺寸和线圈尺寸变化,如何提高板材电磁成形利用率。
本文在前人研究基础上,详细对比了不同尺寸的凹模和线圈对铝合金板材成形的影响,得出有利于提高能量利用率的凹模和线圈的结构尺寸。
1 有限元模拟方法与实验验证
1.1 顺序耦合法有限元模拟
本文在有限元分析ANSYS 平台,采用电磁场和结构场的顺序耦合法[13],对板材电磁脉冲成形进行2D 模拟,其过程如图1 所示。首先建立磁场、结构场模型,将线圈中的放电电流分为多个时间段,先读入磁场模型,计算得到板材各节点的电磁力大小,然后读入结构场模型,将节点电磁力作为边界条件计算板材的变形,变形结束后,对空气网格进行网格随移。再次读入磁场模型进行下一轮的电磁力计算,如此在磁场与结构场间进行耦合循环迭代分析直到加载时间结束。
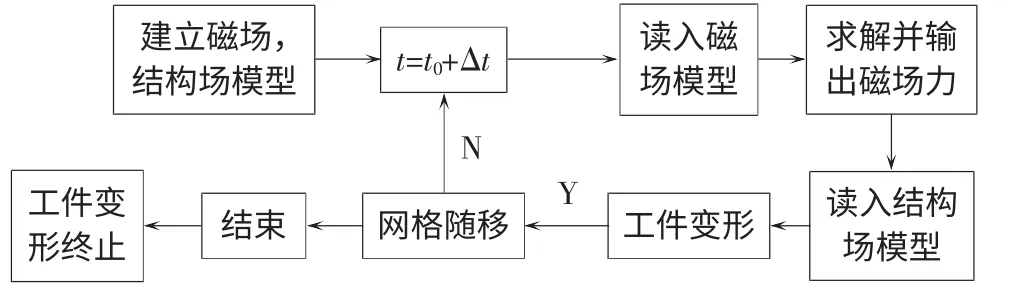
图1 顺序耦合法模拟过程
1.2 模拟参数与实验条件
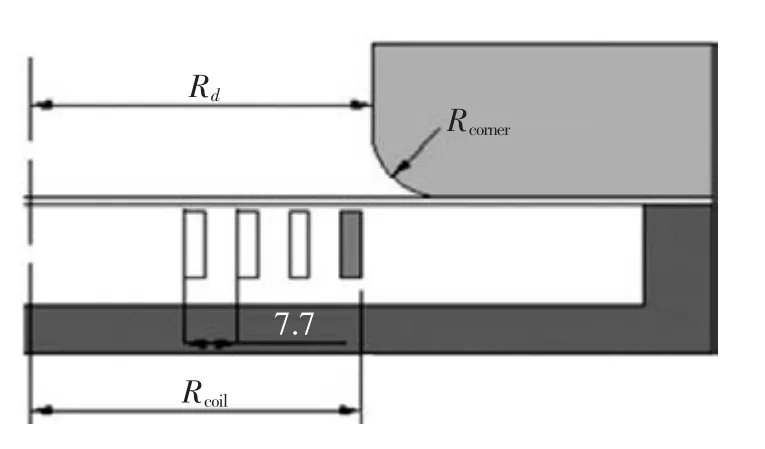
如图2 所示,线圈、板料、模具和模架都是轴对称结构。线圈为螺旋线圈,其匝数为6 匝,每匝导线的截面积为3×10mm,线圈内径为22.4mm、外径Rc为64mm,每匝间距为7.7mm,凹模半径Rd为50mm,圆角半径r 为10mm,整个线路总电阻为4.41mΩ,总电感为13.3μH。实验和模拟采用的放电条件为:放电电压4500V,电容量400μF。
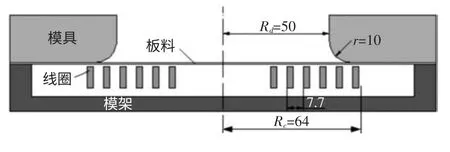
图2 模拟与实验用结构模型
1.3 有限元模型
根据图2 的几何模型建立2D 的电磁场和结构场有限元模型如图3 所示。电磁场几何模型包括板材、线圈、空气和远场空气,板材和线圈采用映射网格技术划分为4 节点单元,单元类型为Plane13,远场采用映射网格技术划分为4 节点单元,单元类型为Inf110,空气采用自由网格技术划分为3 节点单元,单位类型为Plane13。
采用1mm 厚度的AA3003(LF21M)铝合金板,半径为100mm。泊松比为0.3,弹性模量为68.4GPa,板材密度为2.75×103kg/m3。图4 为采用单向拉伸试验所得在室温和准静态条件下的真实应力应变曲线。
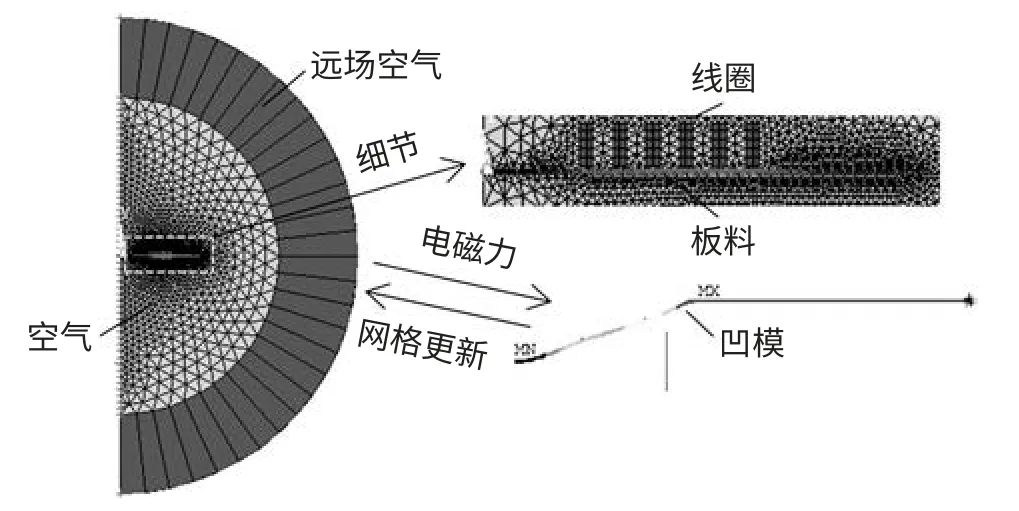
图3 有限元模型
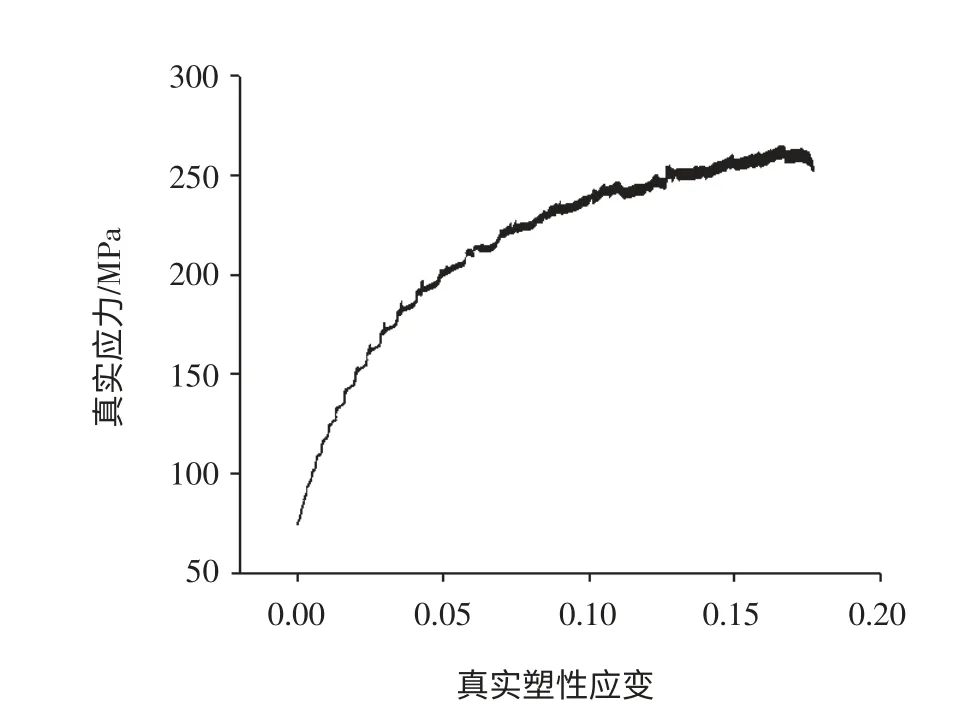
图4 铝合金3003 在准静态下的真实应力应变曲线
对于电磁脉冲成形过程,板材在极短时间内发生大的塑性变形,所以应变率会引起材料本构关系发生变化。在ANSYS/MECHANICAL 软件中,只有粘塑性本构模型(Cowper-Symonds 模型)能够考虑材料的应变率效应。该本构方程如下式:

式中:δ——动态流动应力;
σy——准静态条件下的流动应力;
ε˙——应变率。对铝合金,m=0.25,P=6500s-1。
1.4 模拟结果与实验结果的对比
图5a 为实验得到板材胀形后的形状,提取出经过板材中心曲线Path 上的结果数据,通过三维反求得到其轮廓变化曲线;图5b 为模拟得到的板材最终变形轮廓。图5c 为板材胀形模拟和实验变形轮廓的对比,变形趋势一致,但实验值均稍大于模拟值。这是因为实验中凹模圆角处的摩擦略大于模拟中的设置条件,板材径向流动量与成形高度都小于模拟值,但偏差不大。最大误差出现在靠近中心点处(大约离中心点7mm 处),最大误差值为6.3%。因此可以证明有限元分析预测板材胀形的可行性。
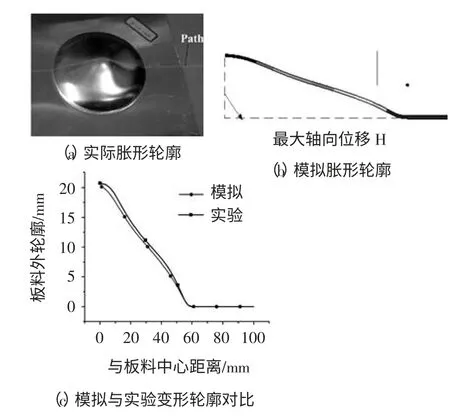
图5 模拟与实验结果对比
2 凹模半径对板材电磁成形的影响
2.1 凹模和线圈尺寸的设定
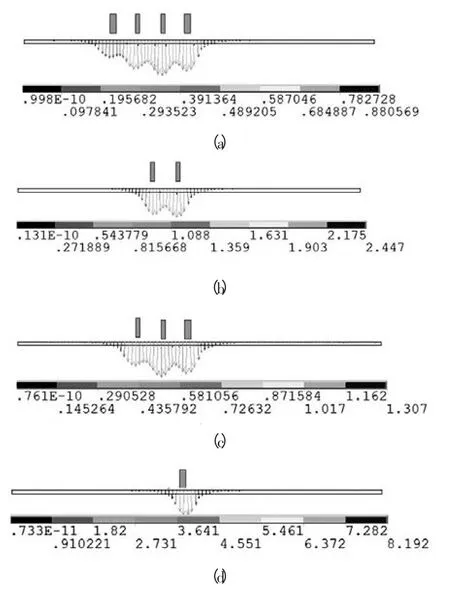
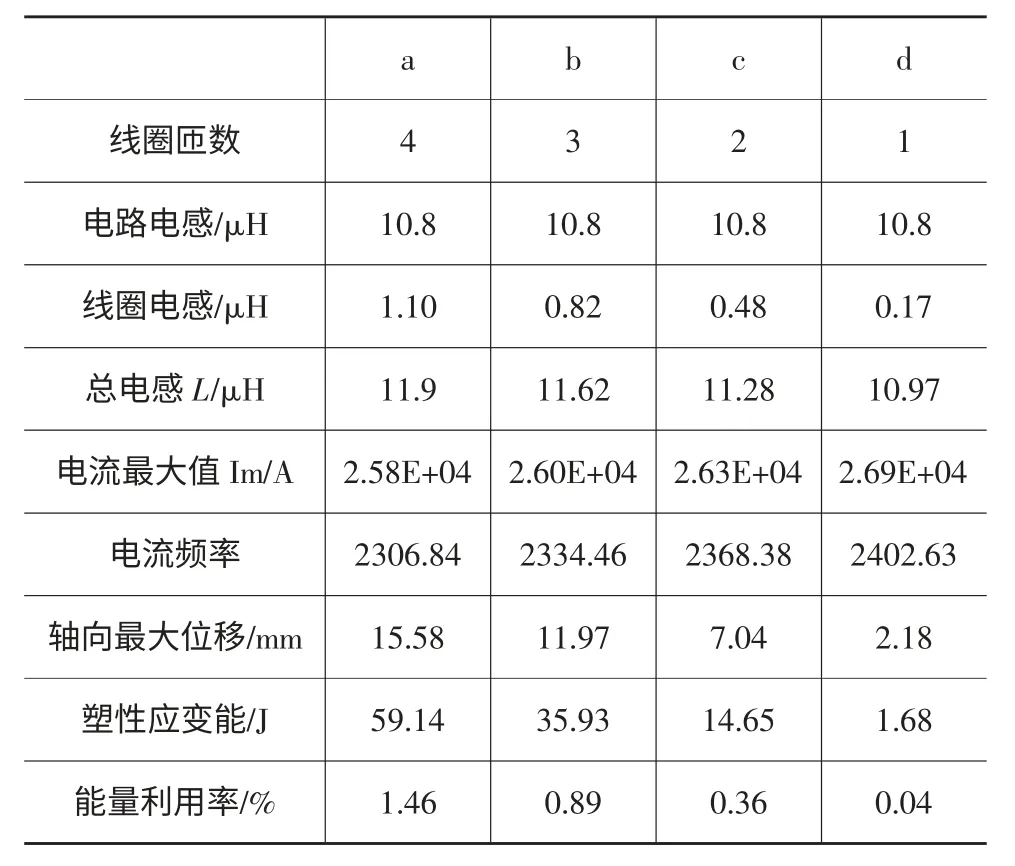
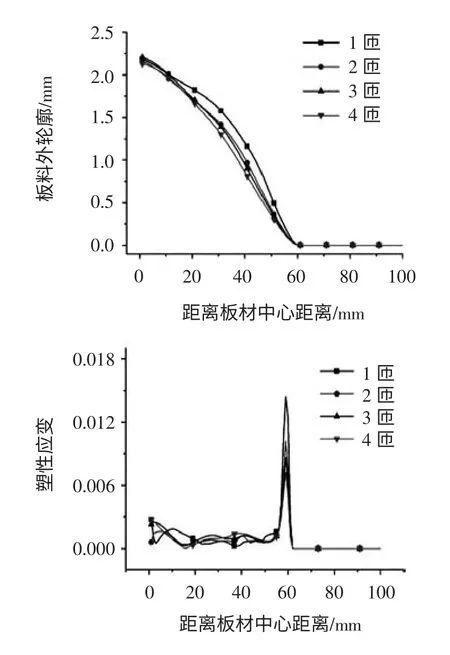
图6 所示为三种不同尺寸的放电线圈覆盖板材和凹模的状况,因为模型为轴对称的,所以选取1/2模型进行对比。当Rc>Rd+r 时,线圈覆盖区域已超过板材可自由胀形区域(图6a);当Rc=Rd+r 时,线圈刚好覆盖板材可自由胀形区域(图6b);当Rc 图6 三种不同尺寸的放电线圈覆盖板材和凹模状况 根据图2 的线圈结构可知,线圈的外径Rc为64mm,凹模圆角半径r 为10mm。凹模内径分别取Rd=42mm、46mm、50mm、54mm、58mm、62mm、66mm、70mm、74mm。当Rd=54mm 时,线圈刚好覆盖凹模洞口。 图7 不同凹模直径下板材变形量 如图7a 所示为不同凹模内径下铝合金板材的最终变形轮廓,可以看出,板材变形均呈锥形。随着凹模内径的增大,板材轮廓随之增大;板材中心最高点成形高度增加。由图7b 可知,当Rc>Rd+r 时,板材中心节点的变形量随着凹模半径Rd值的增大而近似线性关系增加。当Rc 如图8 所示,当Rc>Rd+r 时,随着凹模半径Rd增大,板材上各处节点的塑性应变都增加,分布规律大体一致:从板材中心到凹模圆角处呈下降趋势,在凹模圆角处又达到一个波峰;当Rc 系统初始总放电量: 图8 凹模直径不同时的塑性应变分布 式中:C——电容量; U——放电电压。 电磁板材自由胀形能量利用率为: 式中:Ea——板材塑性变形能。 式中:N——单元数; Ea′——每个单元的塑性应变能。 图9 所示为板材塑性应变与塑性应变利用率随凹模半径变化的关系。可以看出,塑性应变和能量利用率都是随着凹模内径的增大而增大,当达到最大值后开始下降。这是因为随着凹模半径的增大,线圈覆盖板材自由胀形的区域增多,板材的塑性应变增大;当凹模半径增大至线圈覆盖区域已超过板材可自由胀形区域后,应变单元数N 不再增多,而每个单元的塑性应变能开始下降,所以能量利用率出现下降趋势。当Rd=Rc-r=54mm 时,塑性应变最大,达到0.4。当Rd=(1.1~1.2)×Rc时,板材能量利用率最高,达到4.5%。 图9 塑性应变和能量利用率随凹模半径变化 图10 不同匝数线圈放电示意图 根据电磁深拉伸渐进成形[14],线圈沿轴向方向按次序移动。选取1mm 厚度的AA3003 铝合金,放电电压4500V,电容量为400μF。采用截面积3×10mm 线圈,外径为48.5mm,线圈匝间距7.7mm,凹模半径为50mm,凹模圆角半径为10mm。采用四个方案:(a)板材螺旋线圈匝数为4,内径22.4mm;(b)板材螺旋线圈匝数为3,内径33.1mm;(c)板材螺旋线圈匝数为2,内径43.8mm;(d)板材螺旋线圈匝数为1,内径54.5mm。 图11a、b、c、d 分别为线圈匝数为4、3、2、1 时电磁力分布。从结果来看,板料上磁场力最大值差不多,但是板料受到磁场力的作用范围随着线圈匝数的增多而增大。这就会导致板料的变形高度随着匝数的增多而增大。 图11 不同匝数线圈下的电磁力分布 电磁脉冲成形过程中,能量存储于脉冲电容器中。放电开关瞬间闭合,线圈中有脉冲电流通过。根据等效电路法,流过线圈的脉冲电流可描述为: 式中:I0——放电电流幅值; C——总电容量; L——总电感; R——总电阻,电流衰减因子β=165.79s-1。 表1 四种不同线圈时的参数 如图12 所示为电压为4500V 时,a、b、c、d 四种情况下铝合金板材的变形轮廓和塑性应变分布。可知,线圈匝数越多,板材胀形量越高,能量利用率越高。当线圈过少时,最大塑性应变发生在凹模圆角处,容易发生破裂;线圈匝数多时,最大塑性应变发生在板材中心区域。 当线圈匝数不同时,电流峰值、电流频率几乎没有变化,线圈电感也相差不大。但线圈匝数多时,电磁力覆盖区域变大,能量利用率高。 图12 U=4500V 时板材变形轮廓和塑性应变分布 图13a 为铝合金板材成形一定的高度时,a、b、c、d 四种线圈下板材最终变形轮廓,放电电压依次为1350V、1700V、2250V、4500V。由图13a 所示,当线圈匝数为1 匝时,板材从中心到端部变形更平缓,变形更加均匀,但区别不大。图13b 为此项板材各处的塑性应变分布,当成形较小的相同高度时,匝数对应变分布影响不大。此时1、2、3、4 匝线圈的能量利用率分别为0.045%、0.026%、0.022%、0.018%,也相差不大。 图13 相同高度下板材变形轮廓和塑性应变分布 (1)对铝合金板材电磁胀形建立了2D 有限元模型,与实验结果对比相吻合,验证了有限元分析对研究凹模和线圈尺寸对板材胀形影响的可行性。 (2)Rc>Rd+r 时,随着凹模半径的增大,板材的最大变形量急剧增大;当Rc (3)线圈外径一定时,随着线圈匝数的增加,板材变形量增加,塑性应变增加,但板材变形均匀性差别不大。相同电压下,多匝线圈能量利用率高。所以在板材自由胀形中建议采用多匝线圈、小放电电压。 [1]李 娜,莫健华,李奋强,等.铝合金板材电磁脉冲拉深实验与有限元模拟[J].锻压装备与制造技术,2014,49(4):93-98. [2]Daehn Glenn S,Shang Jianhui,Vohnout Vincent J.Electromagnetically assisted sheet forming:Enabling difficult shapes and materials by controlled energy distribution [C].TMS Annual Meeting,Energy Efficient Manufacturing Processes,2003:p117-128. [3]陈玉珍,李春峰,董国庆.平板件电磁成形磁场力研究[J].锻压装备与制造技术,2008,43(1):92-95. [4]Harvey GW,Brower DF.Metal Forming Device and Method.US-Patent Nr.2976907.1958. [5]Psyk V,Risch D,Kinsey BL,Tekkaya AE,Kleiner M.Electromagnetic forming-A review.Journal of Materials Processing Technology.2011,211:787-829. [6]Yu HP,Li CF.Effects of current frequency on electromagnetic tube compression.Journal of Materials Processing Technology.2009,209:1053-1059. [7]Xu W,Liu XS,Yang JG,Fang HY,Xu WL.Effect of temperature on plastic deformation of sheet by electromagnetic force.Journal of Materials Processing Technology,2009,209:2693-2698. [8]Zhang H,Murata M,Suzuki H.Effects of various working conditions on tube bulging by electromagnetic forming.Journal of Materials Processing Technology.1995,48:113-121. [9]肖师杰.板材电磁成形有限元模拟方法研究与线圈的设计和分析[D].武汉:华中科技大学,2012. [10]Liu DH,Yu HP,Li CF.Quasi-static-dynamic formability of AA5052-O sheet under uniaxial and plane-strain tension.Trans.Nonferrous Met.Soc.China.2009,19:318-325. [11]Suzuki H,Murata M,Negishi H.The effect of a field shaper in electromagnetic tube bulging.Journal of Mechanical Working Technology.1987,15:229-240. [12]李 忠,张 伟,李春峰,等.线圈结构参数对电磁成形的影响[J].塑性工程学报,2013,(1):63-67. [13]于海平,李春峰,李 忠.基于FEM 的电磁缩颈耦合场数值模拟[J].机械工程学报,2006,42(7):231-234. [14]Fang J,Mo J,Li J,et al.Electromagnetic Pulse Assisted Progressive Deep Drawing[J].Procedia Engineering,2014,81:801-807.
2.2 凹模尺寸对板材各变形量的影响
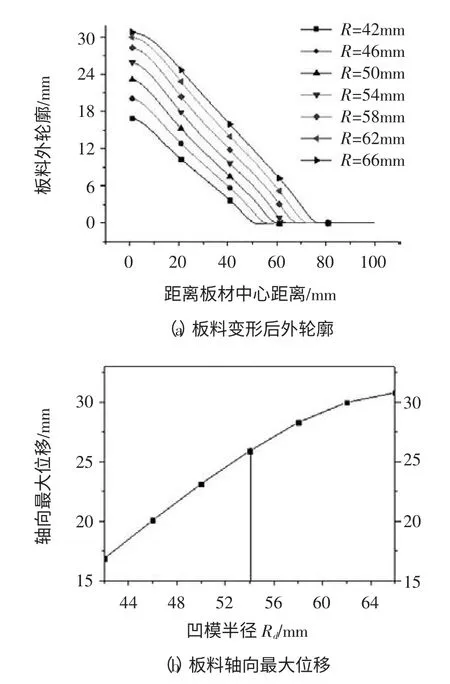
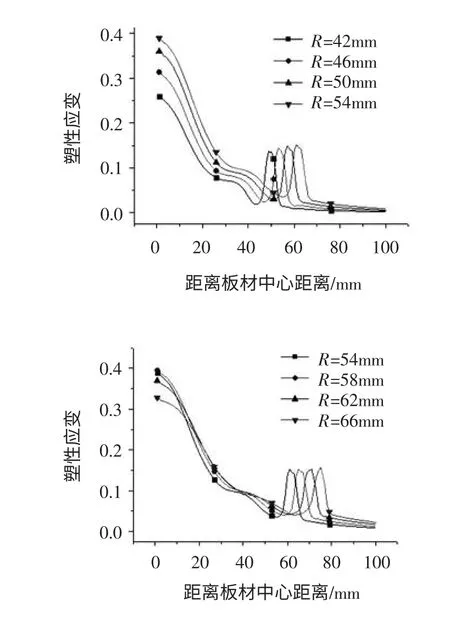



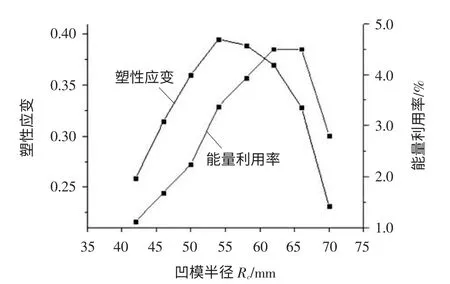
3 线圈结构的影响

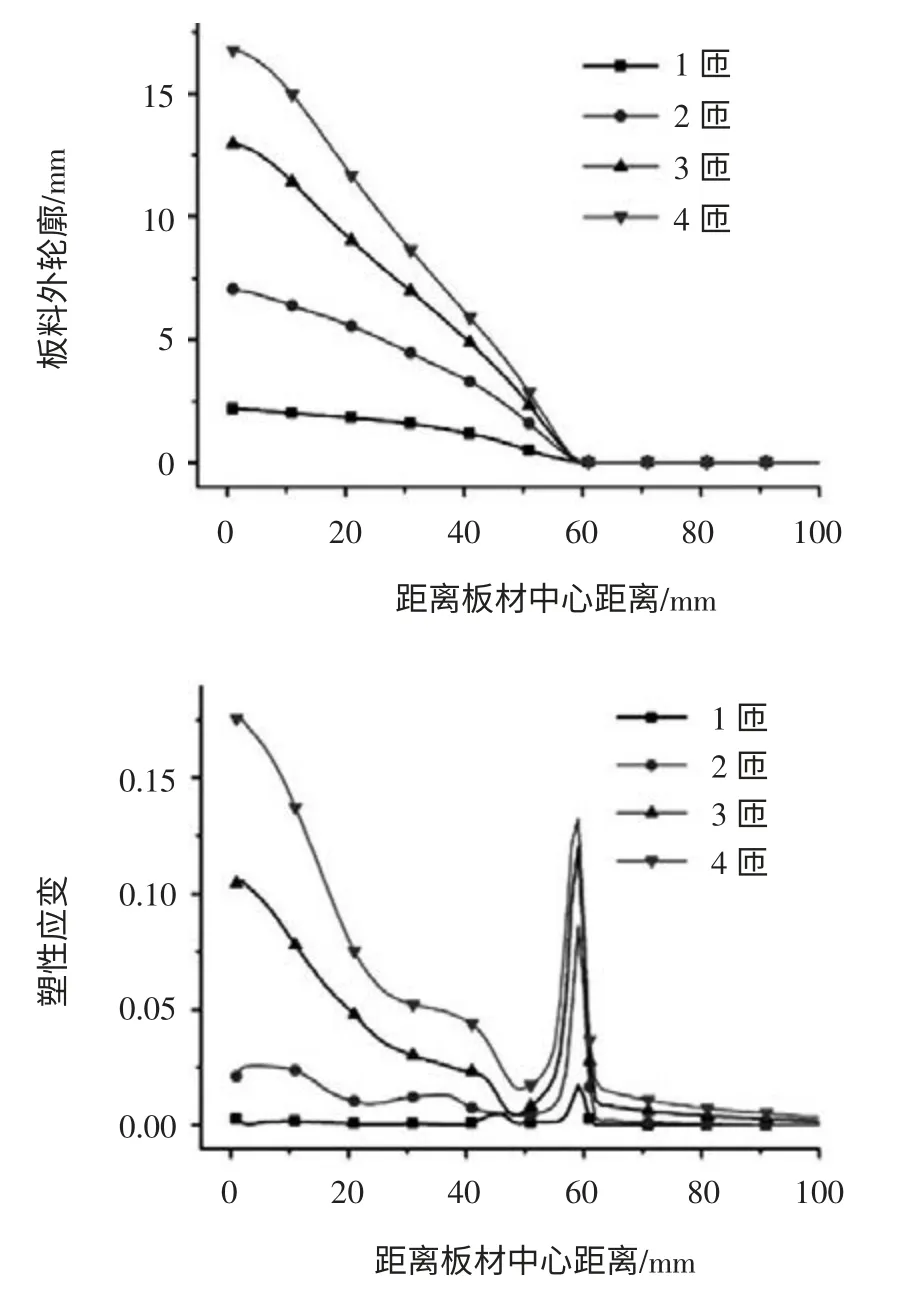
4 结论

