起吊系统在规则波作用下动态仿真分析

荆彪,朱克强，张天宇

（宁波大学海运学院，宁波315211）

起吊系统在规则波作用下动态仿真分析

荆彪,朱克强，张天宇

（宁波大学海运学院，宁波315211）

以起重船在海上起吊作业为背景，建立了吊重系统三维非线性运动学模型。分析了吊重系统在规则波作用下的摆动特性。采用数值仿真软件对时域非线性分析进行求解，讨论了波向、波浪频率以及升降速度对吊重摆角和吊索张力的影响。得到的结论可用于吊重系统摆动的预测与控制，可供设计者参考。

起重船；升降运动；吊重摆动；数值仿真

起重船是海洋工程中常用的工程船舶。在海上作业、停泊时，起重船会受到风浪作用而产生运动，导致船上起重机和吊重产生大幅度摆动，由此不仅增加了吊装作业的危险性，同时也会降低吊装精度。建立波浪环境下起重船与吊重系统动态响应计算模型，准确预测与控制吊重在波流作用下的摆振，对保证起重船在海上安全作业具有重要意义。

起重船在海上作业时，船体因受到波浪作用而发生的运动与吊重运动相互耦合，使得研究起吊系统的动力问题复杂化。Witz［1］考虑了吊重运动与船体运动的耦合效应，分析起吊负载的参数激励对起重船动力响应的影响。Ellermann［2］等通过建立起重船吊重系统的非线性运动方程来分析吊重的大振幅运动，研究了该系统在周期性波浪激励下的动态响应。Cha［3］等利用多体动力学方法建立了起重系统三维非线性运动模型，将起重船与吊重视为六自由度运动的刚体，对起重系统在海浪作用下进行动态仿真研究。MASOUD［4］等建立了吊重系统的空间球摆模型，分析了吊臂的回转和变幅速度对吊重摆动的影响。李跃［5］运用休斯顿方法建立系统动力学方程，考虑趸船横摇和吊臂回转，计算得到了各种工况下吊重摆振的运动轨迹。任会礼［6］等运用拉格朗日运动学方程建立了起重船吊物系统的非线性动力学模型，分析了起吊长度、波浪激励等因素对吊物系统的动力响应的影响。董艳秋［7］研究了起重船在波浪中作业时吊物系统的动力响应，采用新切片理论在频域内得到船体运动，数值计算出吊重摆动规律与吊索动张力。陈徐均［8］等采用多体动力学方法建立了海上作业起重船的动力学模型，对吊重摆动进行分析，对起重船设计与操作给予一定指导。

本文在前人研究成果的基础上，以起吊系统在海上起吊作业为背景，建立起重船与吊重的运动数学模型。应用计算软件OrcaFlex数值模拟吊重系统在不同海况下的动态响应。通过以实船为例，讨论了波向、波浪频率以及吊放速度等因素对吊物摆动与吊索张力的影响，对起吊系统在海洋工程应用具有一定参考意义。

1 基本理论

建立如图1所示的参考坐标系，OXYZ为惯性坐标系，O点为地面或者海平面上任意一点，Z轴方向垂直向上，XY为水平面。oxyz为船体坐标系，O点为船体的几何中心，x轴指向初始平衡位置时船体的体首，y轴指向初始平衡位置时船体的右舷，z轴垂直向上。起重船的结构示意图如图1所示，P点为吊臂端点，Q点为吊重点，Q＇为Q点在平面x0Pz0内的投影，α和β分别称为面内角与面外角。

假定吊索的质量相对于吊重与船体的质量小很多，且忽略船体与起重吊杆的弹性，设船体运动已知，可写为

式中：x为船体位移（横荡、纵荡、垂荡、横摇、纵摇、艏摇）；a为波浪幅值；w为波浪频率。

设吊臂端点P在船体坐标系的初始位置坐标为（xp, yp,zp），则P点的运动可表示为

故可以得到P点的加速度向量

依据坐标轴的之间关系，可得出吊点P在惯性坐标系OXYZ中的坐标为

式中：（xo,yo,zo）为船体初始中心坐标；为船体坐标系与惯性坐标系之间的转换矩阵，φ、θ、ψ为

船体坐标系绕惯性坐标系的转角。

设吊索长度为l，吊重的位置可由α、β来表示，吊重Q在OXYZ坐标系中的坐标为

吊重在升降过程中，根据牛顿第二定律，吊重的运动方程可写为

式中：aQ为吊重加速度；T、G、Fd分别为吊重受到吊索张力、重力以及水动力，它们计算表达式分别为

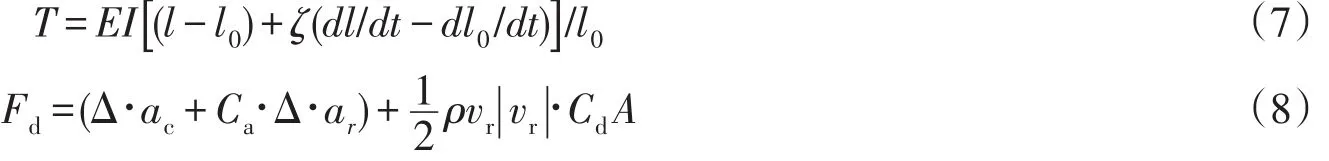
式中：l与l0为吊索的总长与吊放长度；EI为吊索的刚度；ζ为吊索阻尼系数；Δ为吊重排水质量；ρ为海水密度；Ca、Cd为吊重附加质量系数与阻力系数；ac、ar为绝对加速度与相对加速度；A为吊重受阻面积。

将吊重的受力投影到x、y、z轴各个方向上，则（6）式可写成

通过（1）～（9）式可求得α、β的计算表达式。

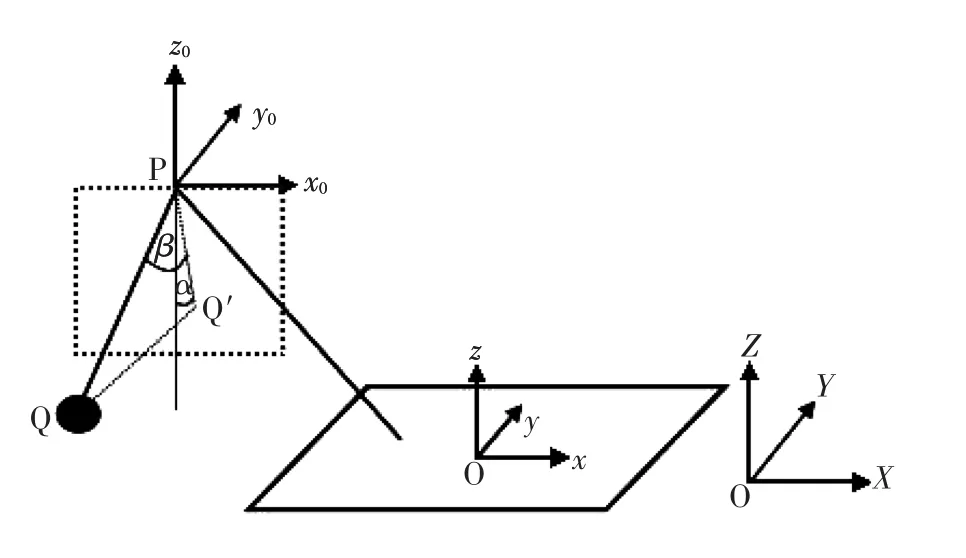
图1 起重船坐标系Fig.1Coordinate system of floating crane

2 模型建立与求解

本文以文献［3］中“Daewoo”起重船作为研究对象，其全长110 m，型宽46 m，最大起重能力为3600t，起重高度110 m，详细计算参数见表1。时域非线性分析使用Orcina公司的OrcaFlex软件进行求解［9］。OrcaFlex基于有限元思想建立动态模型，采用显示积分法进行计算。通过给定对象的初始位置、附加质量和阻尼系数求得当前时刻自由体或节点的加速度，采用牛顿迭代法进行迭代得到下一时刻自由体的运动位置，并通过输入外界环境参数建立吊缆模型，最终求解运动方程得到运动和受力。

3 仿真分析

以“Daewoo”起重船为例，计算起重船升降作业过程中吊重摆动及吊索张力，研究起吊系统在规则波作用下的动态响应。取吊重为150 t，吊索阻尼系数ξ=0.01，其轴向刚度EA=1×105KN/m，吊索的轴向拉伸忽略不计。激励模拟时间为520 s，-20～0 s为准静态计算，该阶段确定起重系统模型运动是否发散，0～500 s为动态计算，研究系统在外部载荷作用下的动态响应。

3.1 变波向动态分析

吊索总长l=250 m，吊重的上升与下降速度v=0.35 m/s，计算海况为规则波。取波浪方向θ=0°，45°，90°，波高H=1.88 m，波浪频率f=0.114 Hz，激励的500 s内，吊重的摆角及吊绳有效张力如图2～图7所示。

从图2～图5中可知，吊重在上升或下降的过程中，波向对吊重的面内摆角α影响很小，而对外面摆角β影响较大。由于船体的横摇运动比纵摇运动显著，且船体在90°波浪作用下横摇运动达到最大，故当波向θ= 90°时，吊重的面外摆角β达到最大。由图6～图7可以看出，起重船在吊放作业时，吊索的有效张力随波向变化而变化。当波向为90°时，吊索张力达到最大，而在波向为0°时达到最小。故在实际施工操作中，应将船首调整到迎浪或随浪状态，避免吊重的大幅度摆动以及吊索张力超载而断裂，影响施工作业安全。

表1 计算基本参数Tab.1Basic parameters

图2 上升阶段，面内摆角α响应Fig.2Response of in⁃plane angle α in rising stage

图3 上升阶段，面外摆角β响应Fig.3Response of out⁃plane angle β in rising stage

图4 下降阶段，面内摆角α响应Fig.4Response of in⁃plane angle α in falling stage

图5 下降阶段，面外摆角β响应Fig.5Response of out⁃plane angle β in falling stage

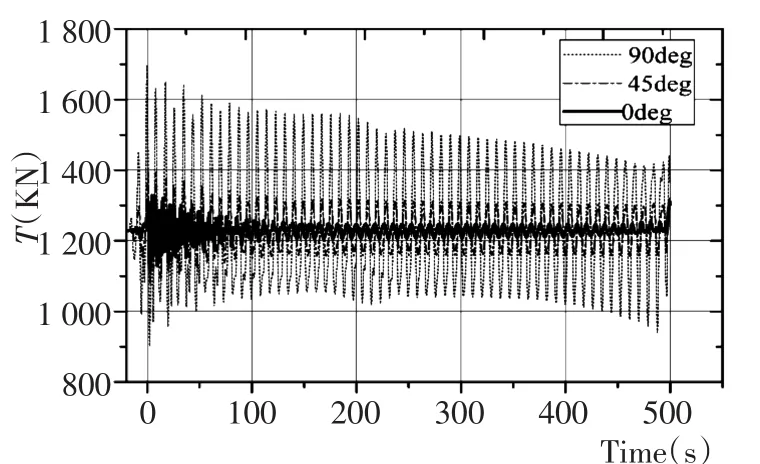
图6 上升阶段，吊索有效张力的变化Fig.6Effective tension of wire in rising stage

图7 下降阶段，吊索有效张力的变化Fig.7Effective tension of wire in falling stage

3.2 变吊速动态分析

考虑吊重的升降运动对吊重摆动的影响，取吊索初始长度250 m，吊重上升速度分别为0.46 m/s，0.35 m/s，0.2 m/s，吊重下降过程取吊索初始长度为20 m，下降速度同上升速度一致。波向取为90°，波高H= 1.88 m，波浪频率f= 0.114 Hz，500 s内吊重的摆动响应如图8～图11所示。

从图8～图11中可以看出，在起重船起升作业过程中，吊重的面内摆角α和面外摆角β具有增大的趋势，而随着起吊速度的增加，吊重的摆动角度却减小。这表明起升过程中速度增大对吊重摆动具有抑制作用，且起吊速度越大，对吊重摆动的抑制作用越明显。在吊重的下降过程中，吊重的摆角具有减弱的趋势，且下降速度越大，吊重摆角的减弱趋势越明显。此外，吊重系统具有一个固有的自振频率，该频率只与吊索长度有关，故在起重船起吊作业过程中，要合理设置起吊速度的大小，有效控制吊索的长度，避免吊重系统的自振频率与波浪频率相接近发生共振的情况。

图8 上升阶段，面内摆角α响应Fig.8Response of in⁃plane angle α in rising stage

图9 上升阶段，面外摆角β响应Fig.9Response of out⁃plane angle β in rising stage

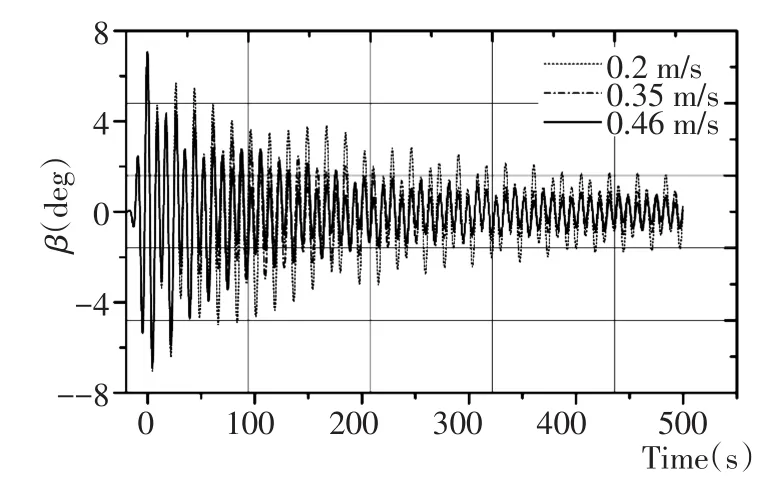
图11 下降阶段，面外摆角β响应Fig.11Response of out⁃plane angle β in falling stage

图10 下降阶段，面内摆角α响应Fig.10Response of in⁃plane angle α in falling stage

图13 上升阶段，面外摆角β响应Fig.13Response of out⁃plane angle β in rising stage

图14 下降阶段，面内摆角α响应Fig.14Response of in⁃plane angle α in falling stage

图15 下降阶段，面外摆角β响应Fig.15Response of out⁃plane angle β in falling stage

图16 上升阶段，吊索有效张力的变化Fig.16Effective tension of wire in rising stage

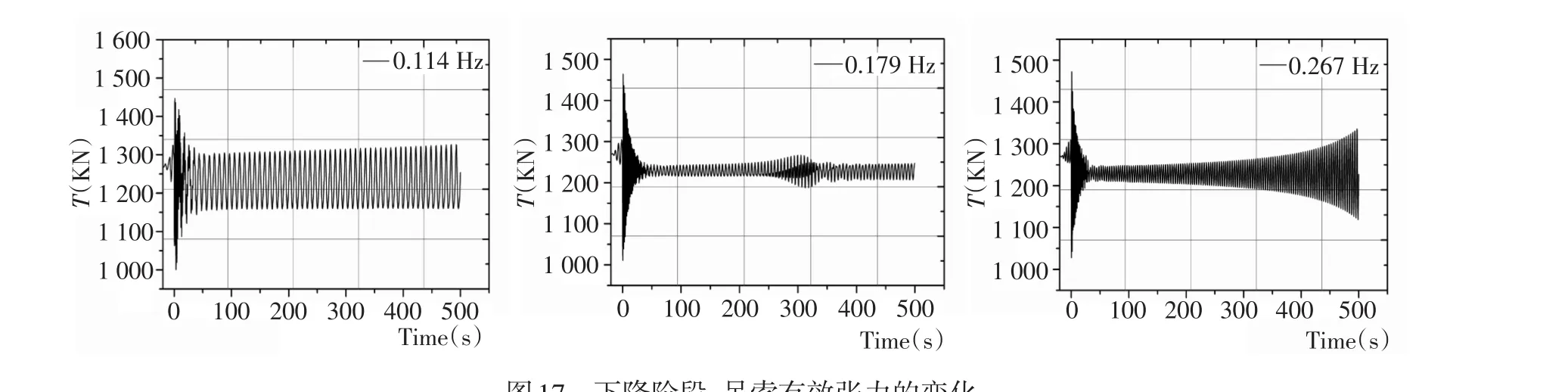
图17 下降阶段，吊索有效张力的变化Fig.17Effective tension of wire in falling stage

3.3 变波浪频率动态分析

首先分析波浪频率对吊重摆角α、β的影响，其次分析吊索有效张力随波浪频率的变化规律。吊索总长l=250 m，波高H=1.88 m，分别取波浪频率f=0.114 Hz，0.179 Hz，0.267 Hz，波向为90°，吊重的上升与下降速度v=0.35 m/s。500 s内吊重摆动响应如图12～图15。

从图12～图15可知，当起吊系统在规则波作用下进行吊装作业时，波浪频率的增加导致吊重摆角减小，这表明长周期波浪对吊重的摆动起放大作用。这是由于长周期波浪对系泊船舶的升沉和横移运动的激励作用显著［10］，且大型起重船船体与吊重之间存在耦合作用。故对于规则波来讲，其波浪频率越小，则运动周期越大，起重船的运动响应越剧烈，从而使得吊重的摆动趋势增加。

吊索的有效张力变化如图16～图17所示，表2列出了不同频率下吊索张力的极值。

从图16～图17中可以看出，横浪作用下的吊重系统表现出非线性响应。当波浪频率与吊重系统固有频率相近时，将会有共振现象的发生，吊索的有效张力表现为急剧上升。由表2可知，在起重船升降作业过程中，波浪频率的增加导致吊索张力幅值增大，故在实际操作中，应尽量避免在高频率波浪海况下进行施工，确保起吊作业的安全。

表2 不同波浪频率时吊索最大张力幅值Tab.2Sling largest tension at different wave frequency

4 结论

本文对起重船吊物系统在规则波作用下的运动响应进行了研究，重点讨论了不同的波向、起吊速度以及波浪频率对吊重的摆动和吊索有效张力的影响。结果表明：

（1）波向对吊重的面内摆角α影响很小，而对外面摆角β影响较大，且吊重的面外摆角β在波向为90°时达到最大。

（2）起重船在起吊作业的过程中，起升速度的增大对吊重摆动具有抑制作用。在吊重下降的过程中，吊重摆角具有减弱的趋势，且下降速度越大，吊重摆角的减弱趋势越明显

（3）长周期波浪对吊重的摆动起放大作用，吊重的摆角随波浪频率的增加而减小。

（4）横浪作用下的吊索张力达到最大，且随着波浪频率的增加，吊索张力的最大幅值也增大。故在实际施工操作中，应将船首调整到迎浪或随浪状态，避免吊重的大幅度摆动以及吊索张力超载而断裂，影响施工作业安全。

［1］Witz J A.Parametric Excitation of Crane Loads in Moderate Sea States［J］.Ocean Engineering，1995，22（4）：411-420.

［2］Ellermann K.Nonlinear dynamics of floating cranes［J］.Nonlinear Dynamics，2002（27）：107-183.

［3］Ju⁃Hwan Cha.Dynamic response simulation of a heavy cargo suspended by a floating crane based on multibody system dynamics［J］.Ocean Engineering，2010（37）：1 273-1 291.

［4］MASOUD Z M.Cargo pendulation reduction of ship⁃mounted cranes［J］.Nonlinear Dynamics，2004，35（3）：299-311.

［5］李跃，沈庆，陈徐均.波浪环境中作业起重船悬吊载荷的摆振分析［J］.建筑机械，2003（8）：55-61.

LI Y，SHEN Q，CHEN X J.Swing analysis of suspended load of crane ship on the wave［J］.Construction Machinery，2003（8）：55-61.

［6］任会礼，王学林，胡于进，等.起重船吊物系统动力响应仿真分析［J］.系统仿真学报，2007，12（19）：2 665-2 668. REN H L，WANG X L，HU Y J.Dynamic Response Simulation of Lifting Load System of Ship⁃mounted Cranes［J］.Journal of Sys⁃tem Simulation，2007，12（19）：2 665-2 668.

［7］董艳秋，韩光.起重船吊物系统在波浪中的动力响应［J］.中国造船，1993，120（1）：63-71. DONG Y Q，HAN G.Dynamic analysis of lifting load system of crane vessel in waves［J］.Shipbuilding of China，1993，120（1）：63-71.

［8］陈徐均，沈庆，崔维成.浮基多刚体系统动力分析［J］.工程力学，2002，5（19）：139-143. CHEN X J，SHEN Q，CUI W C.Analysis of Dynamic Behavior of A Multi⁃Rigid⁃Body System with A Floating Base［J］.Engineer⁃ing Mechanics，2002，5（19）：139-143.

［9］许鑫，李欣，杨建民.半潜式起重船浮吊作业的数值模拟与模型试验［J］.船舶力学，2014，18（7）：799-807. XU X，LI X，YANG J M.Numerical and experimental analysis for lifting of a semi-submersible crane vessel［J］.Journal of Ship Mechanics，2014，18（7）：799-807.

［10］杨宪章.长周期波的特征及对系泊船舶动态特征的影响［J］.港口工程，1989（6）：37-43.

YANG X Z.Dynamic Characteristics of Mooring Ship in the Long Period Waves［J］.Port Engineering，1989（6）：37-43.

Dynamic simulation analysis of floating crane system in regular waves

JING Biao,ZHU Ke⁃qiang,ZHANG Tian⁃yu
（Maritime Academy,Ningbo University,Ningbo 315211,China）

A three⁃dimensional nonlinear kinematic model of hoisting system was set up in the background of floating crane lifting operations at sea.The oscillation characteristics of hoisting system under the action of regular wave were analyzed.The time⁃domain nonlinear analysis was solved with numerical simulation software,discussing the effect of wave direction,wave frequency and hoisting speed on the swinging angle and cable tension.Conclusion obtained from this work can be used for cargo swing prediction and manipulation,as the reference for the designers.

floating crane;lifting movement;cargo swing;numerical simulation

TV 142；O 242.1

A

1005-8443（2015）05-0398-06

2015-03-25；

2015-04-09

国家自然科学基金资助项目（11272160）;国家自然科学基金青年项目（51309133）;宁波市学科项目（szxl1066）

荆彪(1990-)，男，山西省大同人，硕士研究生，主要从事船舶与海洋工程结构动态响应研究。

Biography：JING Biao（1990-）,male,master student.