超窄桥面钢管混凝土拱桥关键技术研究

黄 毅

(中国中铁二院工程集团有限责任公司, 四川成都 610031)

超窄桥面钢管混凝土拱桥关键技术研究

黄 毅

(中国中铁二院工程集团有限责任公司, 四川成都 610031)

平果右江大桥为主跨136m的中承式钢管混凝土拱桥，桥面宽度仅6m，通过建立空间有限元模型，对结构静力和抗风稳定性进行计算分析，结果表明结构整体刚度及颤振临界风速均满足要求，并提出改善刚度的结构措施，提出结构扭弯频率比和梁宽为影响颤振稳定的关键参数。

钢管混凝土拱桥; 整体刚度; 颤振稳定性; 扭弯频率比; 梁宽

广西平果右江大桥为中承式钢管混凝土拱桥，拱肋计算跨径136m，矢高27.2m，矢跨比1/5。拱轴线为悬链线，拱轴系数1.8。大桥为铝土矿运输专用桥梁，拱肋采用哑铃形断面，高度1.5m，由上下两根直径60cm的钢管组成，钢管之间由腹板连接。钢管及腹板内灌注C50微膨胀混凝土。两侧拱肋中心距5.5m，拱肋之间设置四道“一”字形横撑、八道“K”形撑及两道“米”形撑。全桥共设有12对吊杆，纵向间距8m。桥面系宽6m，由横梁、预制桥面板和后浇层共同组成，横梁与吊杆连接，横梁上纵向铺设预制小Π梁。大桥总体布置如图1所示。

图1 桥梁总体布置(单位：cm)

1 有限元分析模型

采用MidasCivil有限元程序建立了该桥的三维空间有限元模型，模型单元数为1 742，节点数为845，主桥拱肋和立柱采用梁单元模拟，桥面纵、横梁采用梁格法划分，吊杆采用只受拉的桁架单元模拟。空间有限元模型如图2所示。

图2 有限元计算模型

2 关键技术问题

2.1 结构刚度

本桥为铝土矿专用运输桥梁，使用荷载较轻，主要包括运输设备荷载1.7kN/m，铝土矿1.6kN/m，双侧检修人行道荷载3.5kN/m。但运营状态下运输机设备对结构变形要求比较严格：(1)运输机每个基础上预埋钢板的平面度误差应不大于5mm；(2)每个基础整体的沉降量支柱基础为不大于20mm，支腿基础为不大于5mm；(3)输送机线路上每个基础的相对位移量为24m长度范围内应不大于25mm；(4)带式输送机在桥面中心位置最大允许横向振动150mm。因此本桥在满足承载能力要求的前提下，必须严格控制桥面变形，满足运输设备要求。设计主要采用灌注钢管混凝土和铺设整体桥面系两方面措施提高结构刚度。

2.1.1 钢管混凝土

对拱肋灌与不灌管内混凝土进行分析计算，考虑以下三种计算工况：(1)半跨满布铝土矿荷载；(2)全跨满布铝土矿荷载；(3)横向风力荷载。桥面结构的竖向位移及一阶稳定系数如表1、表2所示。

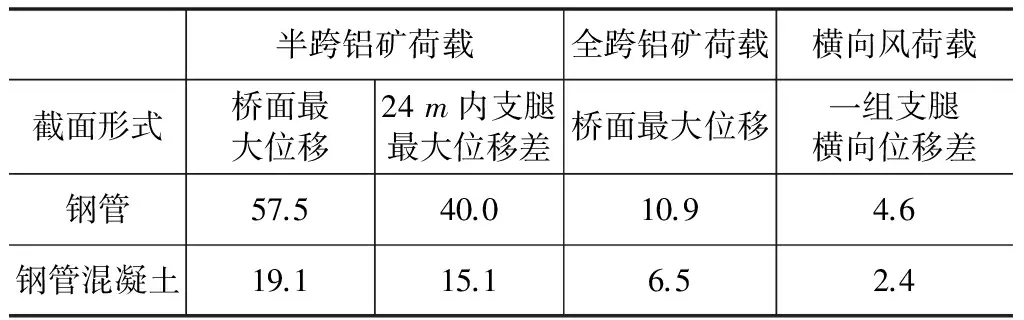
表1 竖向位移汇总 mm

表2 一阶失稳模态及稳定系数

结构采用纯钢管截面形式时，在半跨铝矿荷载下，桥面在24m长度范围内的竖向变形差值为40mm，不满足设备要求的不大于25mm的要求；灌注管内混凝土后，结构刚度明显提高，上述变形差值仅为15.1mm。结构采用纯钢管截面形式时，横向风作用下，桥面扭转引起的一组支腿在横向两个支点处的最大竖向位移差为4.6mm，接近设备要求的平面度误差不大于5mm的要求；灌注管内混凝土后，上述变形差值仅为2.4mm。

从一阶失稳模态也可看出，空钢管截面结构竖向刚度明显较弱，一阶稳定系数仅为4.0，灌注钢管混凝土后提高至11.7。综上考虑结构采用钢管混凝土截面形式。

2.1.2 整体桥面系

整体桥面系由吊杆、横梁、纵梁组成。横梁为矩形截面，宽70cm，高60cm，长度6m。纵梁为Π形截面，梁高35cm，顶板厚10cm，肋宽30cm，纵向长度7.2m。拱肋吊装合龙后，安装吊杆和横梁，然后从跨中和两侧相向、对称吊装纵梁，形成纵横梁桥面体系。纵梁横向分为两片，预留50cm纵向湿接缝。纵梁断面如图3所示。

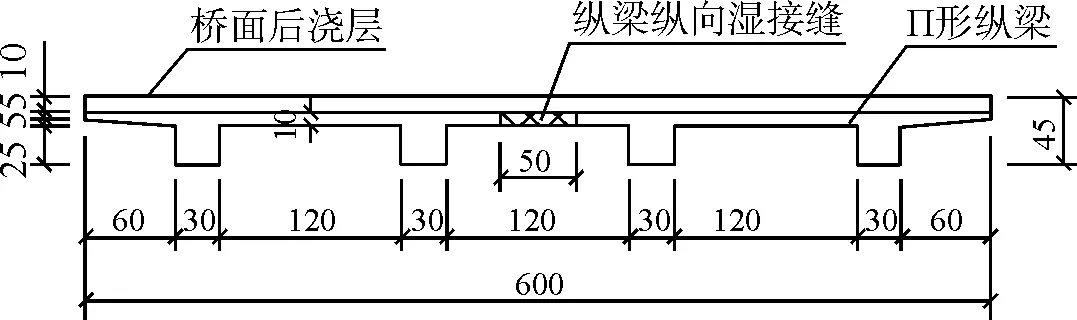
图3 纵梁断面(单位：cm)

纵梁端部直接搁置在横梁上，预留30cm横向湿接缝。全桥纵梁吊装完毕后，浇筑纵、横向湿接缝，使纵、横梁连接形成整体。再浇筑10cm的桥面整体后浇层，完成桥面系施工。最后施工C40纤维混凝土桥面铺装层。通过将纵横梁连接形成整体桥面系，提高桥面系刚度，改善桥面变形，满足运输使用要求。

2.2 抗风稳定性分析

本桥为钢管混凝土结构，桥面系及拱上立柱均为钢筋混凝土结构，整体刚度较大，几何非线性问题并不突出，因此静力抗风稳定性不存在问题。但由于使用功能对桥面宽度要求较小，桥面宽度只有6m，而拱肋跨度136m，宽跨比达到1/22.7，属于典型的窄桥，必须重视横风颤振稳定问题。为了研究影响抗风稳定的主要因素并优化参数，本文分析仍套用适用于流线型截面的古典耦合颤振检算公式，其研究结果仍然可以在一定程度上反映大桥的抗风颤振稳定问题。

2.2.1 颤振稳定的分析方法

1935 年，Theodorson首先从理论上研究了薄平板的空气作用力，用势能理论求得了作用于振动平板上的非定常空气力的解析表达式。1976 年，VanderPut提出了平板颤振临界风速Vcr的简化计算公式[1]：

(1)

(2)

式中：Vco为临界风速(m/s)；Vcr为考虑形状系数折减后的临界风速(m/s)；ε为扭弯频率比，ε=ωt/ωb，ωb为抗弯基频，ωt为抗扭基频；μ为桥面质量与空气的密度比，μ= m/(πρb2)，ρ= 0.125kg/m3，m为桥面每延米的质量；r/b为桥面惯性半径比，r=(Im/m)1/2，Im为桥面每延米质量惯性矩(kg×m2/m)，b为梁半宽(m)；ηs、ηα为形状系数，本桥梁部宽高比达到12，可近似看作平板，取ηs=1，ηα=1。

通过计算，得到该桥的自振频率和振型，结果如表3所示。

计算结果表明，该桥第一阶振型固有频率达到0.469Hz，表明其整体刚度较大。相对而言，该桥的侧向刚度要弱一些，第一阶振型首先发生了平面外正对称侧弯, 拱肋与桥面系的面外挠曲刚度小于竖向挠曲刚度, 表现出较为明显的窄桥特征。在风荷载作用下，桥梁的横向振动要大于竖向和扭转方向。

表3 自振频率和振型描述

与颤振计算相关的是第二阶竖弯基频0.525和第五阶扭转基频0.874，利用VanderPut计算公式可得颤振临界风速Vcr=44.2m/s。桥址处设计风速Vd=28m/s，风速的脉动影响及水平相关特性的修正系数μf=1.4，考虑到本桥设计使用寿命仅为30a，结构重要性程度较低，取0.9倍折减系数，由公路抗风设计规范可得成桥状态的颤振检验风速为：

(3)

颤振临界风速Vcr>[Vcr]，满足抗风稳定要求。

2.2.2 提高颤振稳定的结构参数研究

从VanderPut计算公式(1)分析可知，竖向弯曲频率对结构颤振稳定具有不利影响。扭弯频率比可以提高颤振临界风速，对颤振稳定起有利作用。梁宽也是影响临界风速的一个因素。因此将扭弯频率比ε和梁宽B作为两个结构参数，研究其对结构颤振临界风速的影响。

计算采用钢管内灌注拱脚部分混凝土的方式改变结构刚度，提高扭转基频并对竖向基频影响相对较小，从而提高扭弯频率比。同时增加梁宽，考察其对临界风速的影响。结果如表4所示。

计算结果表明：

(1)桥面梁宽均为4.6m时，灌注拱脚段混凝土后结构扭弯频率比ε有所增加，颤振临界风速相应提高。桥面梁宽均为6m时具有同样的规律；

(2)拱肋不灌注混凝土，为纯钢管结构时，梁宽由4.6m增加到6m，间接提高了扭弯频率比，颤振临界风速相应提高。拱肋灌注拱脚段混凝土时具有同样的规律。

3 结论

平果右江大桥具有使用荷载轻、桥面变形要求严的特点，大桥设计受刚度控制。同时桥面宽度极窄又带来横风颤振稳定问题。通过对大桥进行动静力计算分析，得出以下结论：

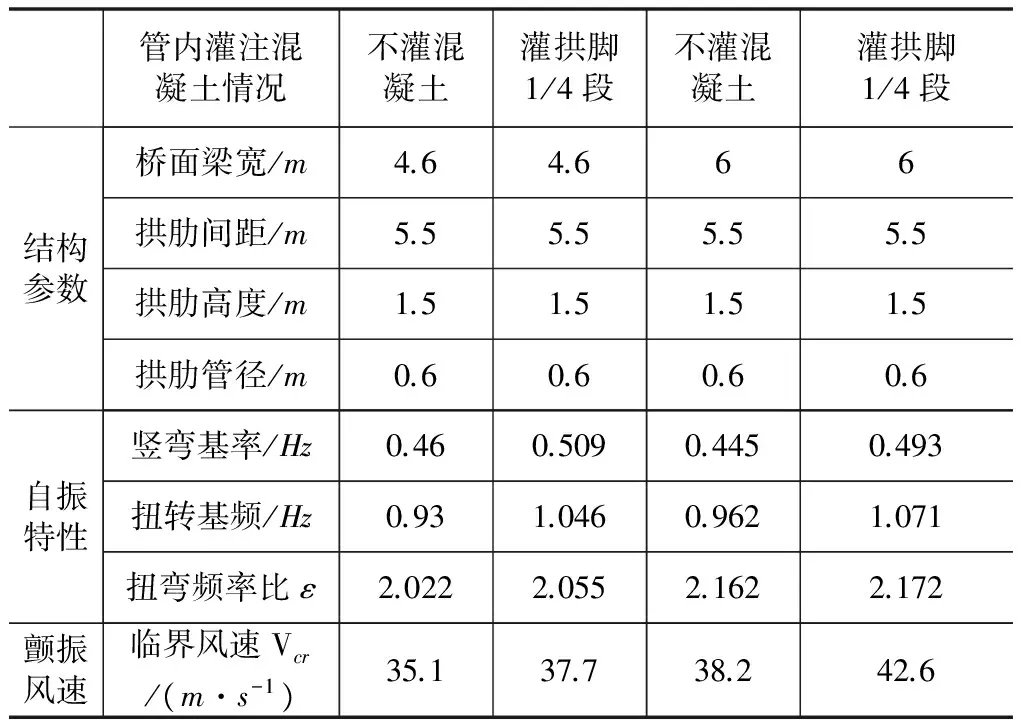
表4 扭弯频率比及梁宽对临界风速的影响

(1)采用灌注管内混凝土和形成整体桥面系的结构措施，可以极大的提高结构整体刚度，改善桥面变形。

(2)对于桥面宽度窄、桥面板厚度薄的此类结构，必须进行横向风颤振稳定计算，保证结构颤振临界风速大于检验风速。

(3)提高结构的扭弯频率比，能够有效地改善颤振稳定问题，同时适当的增加桥面宽度也是有利的。

[1] 项海帆．现代桥梁抗风与实践[M]．北京：人民交通出版社，2005

[2] 李国豪．桥梁结构稳定与振动[M]．北京：中国铁道出版社，2003

[3]JTG/TD60-01-2004 公路桥梁抗风设计规范[S]

[4] 项海帆，林志兴．大跨度桥梁颤振稳定性的简化判别[J]．同济大学学报，1994，22(4)：409-414

黄毅，男，工程师，研究方向为桥梁工程、铁路大跨桥梁结构。

U441+.5

A

[定稿日期]2014-07-10