离散Walsh变换在超声治疗无损测温中的应用
李 勇,丁亚军,b,钱盛友,段先知,邹 孝
(湖南师范大学a.物理与信息科学学院;b.图像识别与计算机视觉研究所,长沙410081)
离散Walsh变换在超声治疗无损测温中的应用
李 勇a,丁亚军a,b,钱盛友a,段先知a,邹 孝a
(湖南师范大学a.物理与信息科学学院;b.图像识别与计算机视觉研究所,长沙410081)
利用高强度聚焦超声对新鲜的离体猪肉进行辐射,并通过B超获取辐射前后的超声图像。采用二维离散Walsh变换法,从辐射前后的超声图像的差图像中分离出低频分量,作为反映温度信息的参数。选取确定系数作为衡量误差的参数,通过曲线拟合,发现二维离散Walsh变换直流分量与温度呈近似线性关系,且多组数据的斜率非常接近,与传统的灰度均值测温法相比,实验结果表明,该方法误差更小,温度分辨率更高,使用正交矩阵变换,符合计算机语言的逻辑,仿真检测时间较短,在实际应用中能为超声无损测温提供准确可靠的依据。
高强度聚焦超声;二维离散Walsh变换;低频分量;无损测温;差图像;曲线拟合
1 概述
高强度聚焦超声(High Intensity Focused Ultrasound,HIFU)是一种利用超声波的热效应来治疗癌症的手段,主要是通过超声波良好的组织穿透性和方向性在生物组织内汇聚形成高强度声场,利用超声波的瞬态高温效应、空化效应和机械效应等破坏焦域处靶组织,从而达到治疗或外科切除病灶的目的[1]。近年来,这种技术受到国内外的广泛关注,我国在HIFU临床应用方面位于国际前列。
本文采用二维离散Walsh变换对超声图像的差图像进行处理,分离出低频分量作为反映温度的信息,进行无损测温。这种算法可以将反映温度的信息与高频噪声等区分开来,在抑制与温度无关的信息方面取得较好的效果,为超声热治疗提供比较可靠的温度信息。
2 背景介绍
HIFU可以在病灶区的肿瘤中产生瞬态高温(60℃以上),使肿瘤组织迅速凝固甚至坏死,而对病灶区周围的正常组织影响很小甚至无任何损伤。在HIFU治疗中,对焦域内的温度控制要求很严格,温度过高,会导致病灶区组织碳化,不利于组织吸收,甚至产生并发症。温度过低,治疗时间会延长,疗效不明显,还可能会增加病人的痛苦。因此,实时温度的测量在治疗中起到非常重要的作用。文献[2]通过微波消融离体猪肝实验得出,超声图像的灰度均值、梯度、功率谱密度等参数与温度存在明显的正相关性。文献[3]利用超声波对新鲜的离体猪肝及猪肌肉进行26℃ ~63℃范围内的测温实验证明,用灰度变化来估测被加热点温度的方法可行,但是在试验温度范围内,温度变化和灰度变化成非严格线性关系。文献[4-5]采用二维离散Fourier变换直流分量法和实值离散Gabor变换,将反映温度的信息与噪声等其他信息区分开来,证明二维离散Fourier变换直流分量法与温度、Gabor变换低频系数能量与温度均成近似线性关系。文献[6]利用数据挖掘的方式发现GLCM惯性矩、均值和、梯度均值、梯度方差及4种小波基下的小波分解系数能量与温度间存在多元线性关系。
3 二维离散Walsh变换
离散沃尔什变换是一种正交变换,它只包含+1和-1 2个数值所构成的正交函数基[7]。Walsh函数可以通过不同的途径推导出来,本文介绍一种三角函数定义的Walsh函数[8]进行表示:
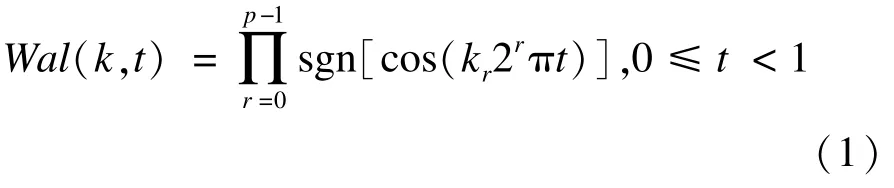
其中,k是Walsh函数编号,为非负整数,其二进制表示式为:p表示k的二进制位数,kr为0或者1,是k的各位二进制的值。进行一维离散Walsh变换时,先对f(t)进行数字化得到f(n)变换的定义式为:
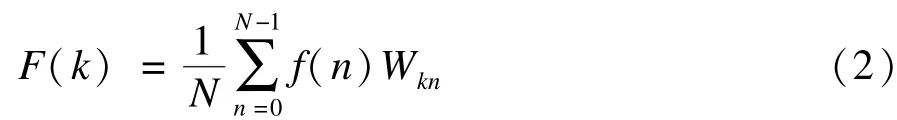
其中,k=0,1,…,N-1;N表示DWT的阶数;Wkn是Wal(k,t)的N个间隔采样点值。逆变换为:
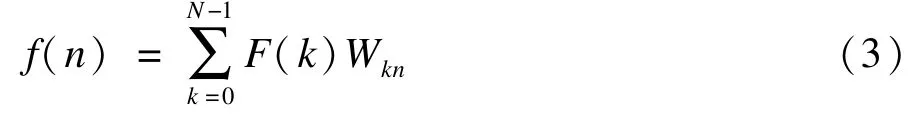
其中,k=0,1,…,N-1;n=0,1,…,N-1。
DWT变换可以表示为如下的矩阵形式:

其中,f,F均为行向量。
逆变换矩阵形式为:

由此可以得出Walsh矩阵具有正交性,即:

其中,I为单位矩阵。
进行二维离散Walsh变换时,对采集到的超声灰度图像,进行数字化处理后得到数字图像f(n1,n2),n1,n2均为整数[9]。
其二维离散Walsh变换式为:
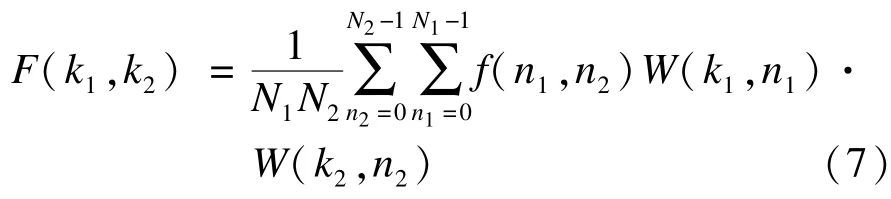
其中,k1=0,1,…,N1-1;k2=0,1,…,N2-1。
二维DWT矩阵变换式为:

二维DWT逆变换为:
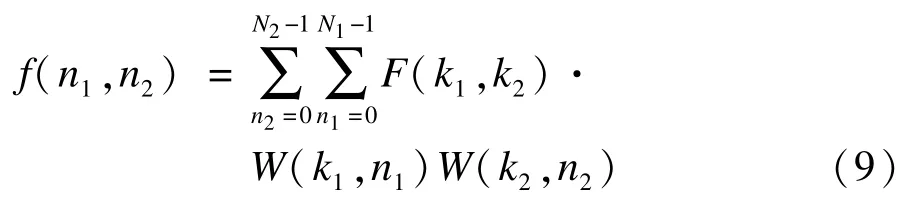
其中,n1=1,2,…,N1-1;n2=1,2,…,N2-1。
二维DWT逆变换的矩阵式为:

同样可以得到 Walsh矩阵WN具有正交性质,即:

其中,I为单位矩阵。
Walsh函数W(k,n)有3种形式[10]:Walsh序的Walsh函数,佩利序的 Walsh函数,哈达玛序的Walsh函数。基于计算速度等优点,本文使用哈达玛序的Walsh函数。
综上所述,Walsh变换是将图像矩阵f(n1,n2)分解为无穷多个Walsh矩阵的叠加,得到的F(k1,k2)矩阵就是Walsh矩阵的幅度系数。Walsh变换的物理意义是将图像f(n1,n2)从灰度分布变换为频率分布F(k1,k2),从而可以通过变换获取信号在各个频率点上的强度大小。可以看出当k1=k2=0时,Wal(0,n)=1,即F(0,0)表示f(x,y)在变换系数中的直流分量,当k1,k2不等于0时,表示F(k1,k2)在不同频率上能量的大小。当温度发生变化时,灰度图像的灰度值会发生变化,在灰度图像中,还包含了一些因空化引起的相关信息及噪声等。在Walsh变换中,可以将反映温度信息的低频部分(k1=k2=0)与高频噪声以及与温度无关的信息(k1≠0,k2≠0)加以抑制。
4 无损测温实验
4.1 实验环境和实验方案
将具有固定频率的B超诊断仪作为获取温度图像的设备,设计了如图1所示的实验装置。高强度聚焦超声(HIFU)为温度处理设备。实验中,在进行B超拍照获取超声图像[11]的同时,通过热电偶记录温度。
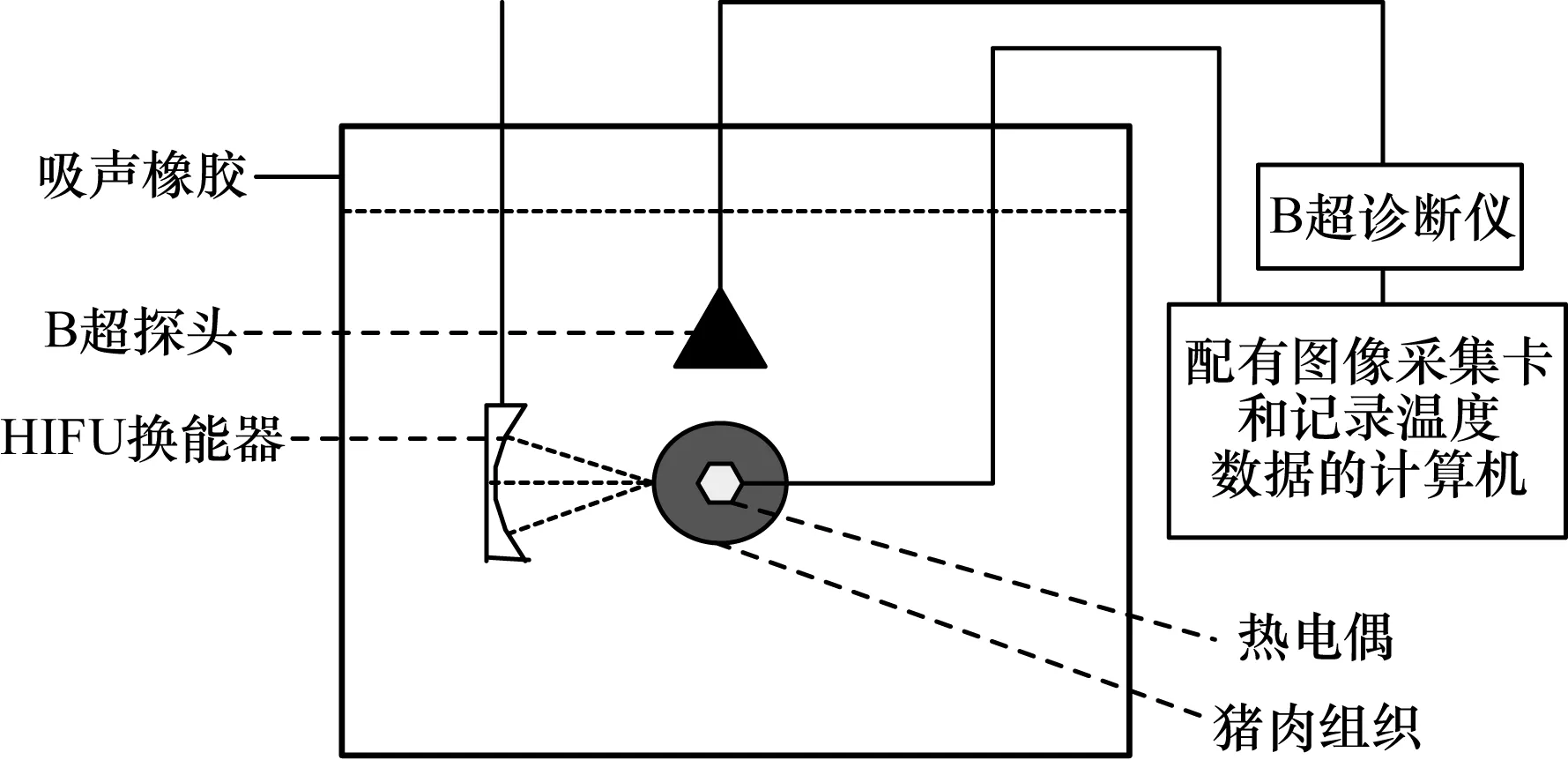
图1 无损测温实验装置
实验所采取的生物组织样本为新鲜的离体猪肌肉组织,测温范围在37℃ ~75℃。对获得的B超图像和对应的温度进行记录,并以超声焦域为中心选取64×64的图像作为实验数据进行处理。获取实验数据后,在不同的情况下,或者不同的组织中,超声图像是有所差别的。为了减小差别,先对B超诊断仪获取的灰度图像作差图像处理,也就是将猪肉组织焦域处于各温度时获取的灰度图像与处于37℃时的灰度图像做减处理,得到的图像就是差图像。如图2所示,图2(a)~图2(c)分别是焦域处于37℃,55℃,73℃时的灰度图像。图2(d)~图2(e)分别是焦域处于55℃,73℃时灰度图像与37℃灰度图像的差图像。
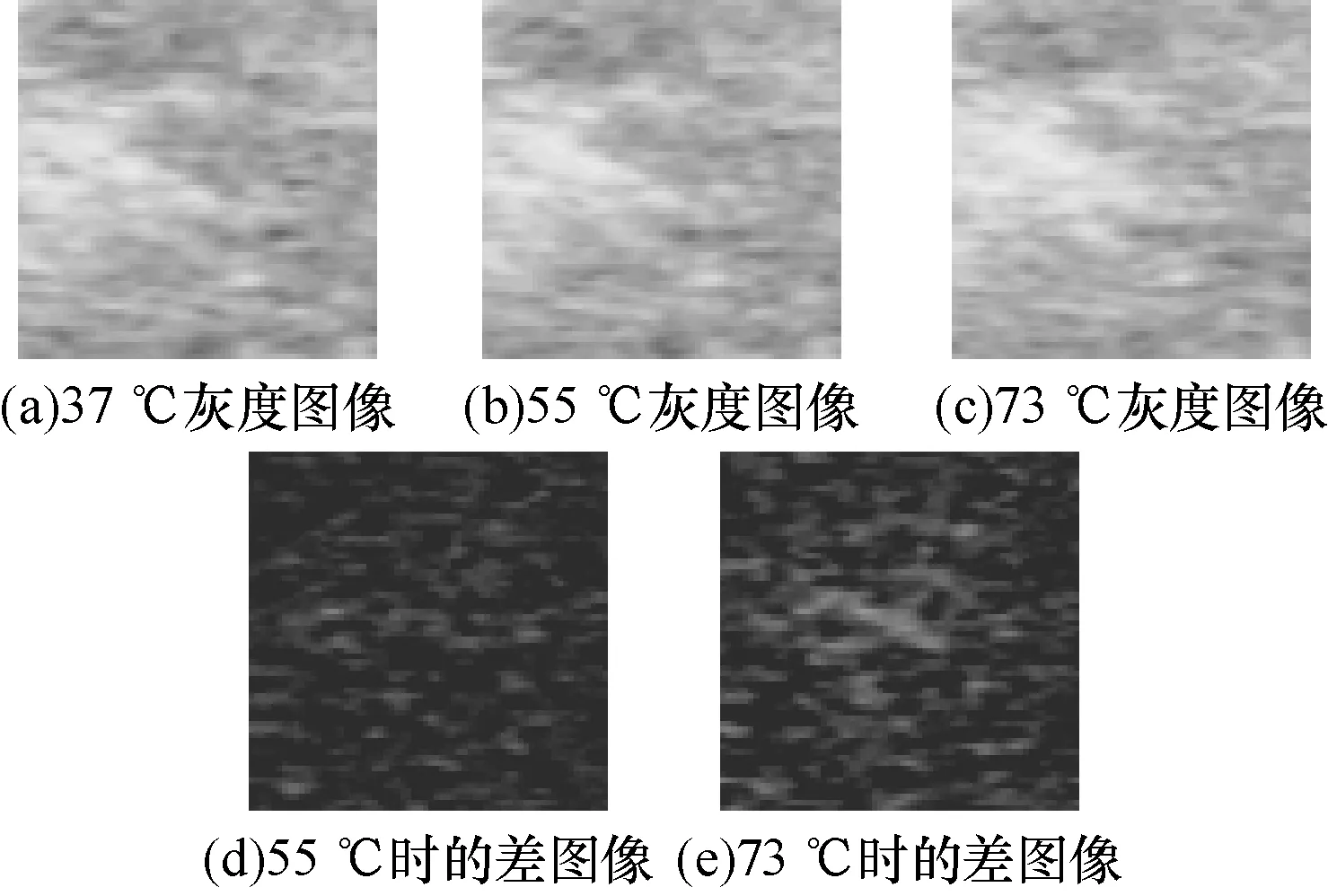
图2 64×64 HIFU焦域处超声图像及差图像
4.2 实验结果及分析
为了体现本文方法的有效性和优势,在Matlab-R2013a版本下,采用二维离散Walsh变换分离低频分量法和灰度统计法作对比,仿真得到图像的特征参数,并通过Matlab这一软件平台,将图像的特征参数与对映的温度信息采用最小二乘法原理进行线性拟合[12]。选取1组数据拟合的结果如图3所示。图4分别是选用4组不同的超声灰度图像,提取二维离散Walsh变换分离出的低频分量(Discrete Walsh Transform D Component,DWTDC)、灰度均值2个特征参数进行分析,并进行曲线拟合得到的结果。

图3 1组数据的参数分析结果
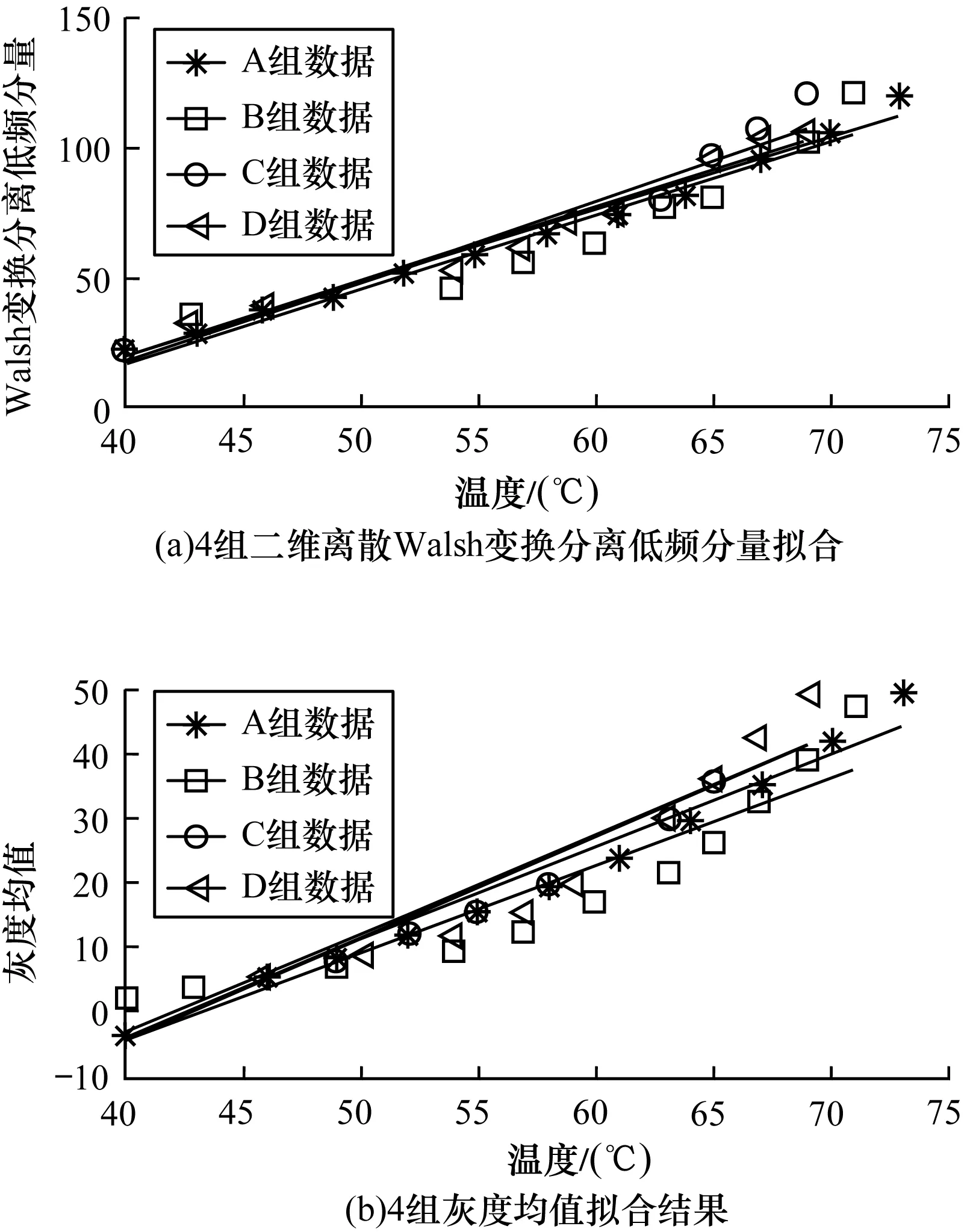
图4 综合4组数据的参数分析结果
在曲线拟合中有如下参数:
(1)SSR(Sum of Squares of Regression):预测数据与原始数据均值之差的平方和。
(2)SST(Total Sum of Squares):原始数据和均值之差的平方和。
(3)SSE(Sum of Squares due to Error):预测数据和原始数据对应点的误差平方和。SST是SSR与SSE之和。
(4)确定系数(R-square:Coefficient of determination)为:

确定系数越大,说明此拟合模型对数据的拟合度越高。对每组数据进行具体参数计算,得出表1、表2所示结果。误差分析选取确定系数R-square作为衡量误差大小的参数。
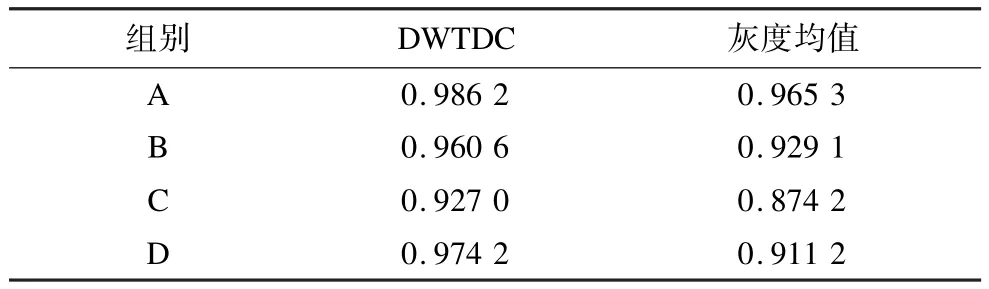
表1 4组数据确定系数R-square的比较

表2 4组数据拟合斜率的比较
在Matlab仿真实验条件下,对所选用的4组数据,用二维离散Walsh变换法分离低频分量,运行时间分别为:0.103 88 s,0.146 03 s,0.135 87 s和0.129 14 s,平均运行时间为0.128 73 s,运行速度比较快,在实际运用中能达到实时检测的要求。
综合图3、图4和表1、表2,进行如下数据分析:
如前已述,温度的变化能引起灰度均值的变化,也能反映温度变化的规律,因此,选取灰度均值作为参考对象具有可行性。
从图3可以看出,分别选取DWTDC和灰度均值作为参数,可以得出两者均与温度有近似线性关系。由图3和表1可以知道DWTDC的确定系数(R-square)均要比灰度均值大,由此可以说明DWTDC与温度的曲线拟合误差更小,即与灰度均值相比,DWTDC有更好的线性关系。从选取的实验数据结果来看,DWTDC这一参量作为温度参数,比灰度均值更加具有说服力。
从图4(b)中可以看出,以灰度均值为参数,在温度超过60℃时,灰度均值开始发散,拟合曲线不再平行或者重叠,误差较大,不宜再作为测温的特征参数。而以DWTDC作为参数如图4(a)时,在整个测温范围内,数据都较均匀地分布于拟合曲线两边,曲线集中程度也较高。
从表2可知,DWTDC与温度的拟合斜率均要大于灰度均值与温度的拟合斜率,可以说明,单位温度内,DWTDC的变化比灰度均值大,具有更高的温度分辨率,能够容忍更大的偶然误差。此外,只选用DWTDC(即选取图像的低频部分作为参数),可以分离并滤除图像中处于高频部分的噪声。所以,差图像的二维离散Walsh变换分离低频分量法能够作为测温的手段,进行比较准确的无损测温。
5 结束语
本文通过Matlab对差图像数据进行处理,发现灰度均值和DWTDC都可以近似地作为HIFU无损测温的方法,然而DWTDC与灰度均值相比,具有更多优点:(1)随着温度的升高,DWTDC呈现出近似直线的增长,拟合的相对误差比较小。(2)二维Walsh变换分离出的低频分量对温度的分辨率明显比灰度均值高。(3)二维离散Walsh变换分离出的低频分量能够滤除高频噪声。(4)从硬件实现方面来说,沃尔什变换矩阵只包含+1和-1 2个数值所构成的正交函数基,符合计算机的逻辑,减少了计算量和存储空间,提高了计算速度,因而更适用于计算机处理。
综上所述,本文采用的二维Walsh变换分离低频分量法可以用于无损测温,比灰度均值法等有明显的优势,在计算机处理上具有广泛的应用前景。
[1] Chauhan S,Michel M S,Alken P.High-Intensity-Focused-Ultrasound(HIFU)Induced Homeostasis and Tissue Ablation[C]//Proceedings of Conference on International Society for Optics and Photonics.[S.l.]:SPIE Press,2003: 237-244.
[2] 任新颖,吴水才,曾 毅.基于组织B超特征的癌热疗无创检测实验[J].北京工业大学学报,2008,34(1):90-96.
[3] 侯珍秀,徐祯祥,金长善,等.高强度聚焦超声热疗中无损测温的实验研究[J].中国超声医学杂志,2002, 18(9):653-657.
[4] 陈锦钧,陈真诚,陈洪波.离散Fourier变换在无创测温中的应用[J].生物医学工程研究,2007,26(3):236-239.
[5] 陈洪波,汤井田,陈真诚.实值离散Gabor变换在HIFU无损测温中的应用[J].仪器仪表学报,2008,29(12): 2646-2649.
[6] 冯艳玲,谭 旭.数据挖掘技术在猪肉组织无损测温中的应用研究[EB/OL].(2010-12-01).http://cpfd.cnki. com.cn/Article/CPFDTOTAL-ZNXX201012001059.htm.
[7] 黄会营,张宇波.沃尔什变换在图像数据压缩中的应用[J].微计算机信息,2009,25(15):290-291.
[8] 郑君里,应启珩,杨为理.信号与系统[M].2版.北京:高等教育出社,2000.
[9] Gonzalez R C.数字图像处理[M].2版.阮秋琦,阮宇智,译.北京:电子工业出版社,2007.
[10] 王海鹏.多维 Walsh-Hadamard变换算法实现与优化[D].武汉:华中科技大学,2009.
[11] 任新颖,吴水才,曾 毅,等.组织超声回波时移温度相关性及其无创测温研究[J].中国生物医学工程学报,2006,25(3):328-332.
[12] 李庆扬,王能超,易大义.数值分析[M].北京:清华大学出版社,2008.
编辑 顾逸斐
Application of Noninvasive Temperature Measurement with Discrete Walsh Transform in Ultrasound Therapy
LI Yonga,DING Yajuna,b,QIAN Shengyoua,DUAN Xianzhia,ZOU Xiaoa
(a.College of Physics and Information Science;b.Institute of Image Recognition&Computer Vision, Hunan Normal University,Changsha 410081,China)
Irradiating fresh pork in vitro by High Intensity Focused Ultrasound(HIFU),subtraction image of B ultrasonic image is obtained before and after irradiation.The low-frequency components as the parameters about the temperature information,are separated from the subtraction image by two-dimensional discrete Walsh transform.There is an approximate linear relationship between Discrete Walsh Transform Direct Component(DWTDC)and temperature,and the slopes of multiple sets of data are very close proximity using R-square as a parameter to measure the error and curve fitting.The error is smaller.Temperature resolution is higher than the traditional temperature estimation method by using gray average.This method using the orthogonal transform matrix conforms to the logic structure of computer language, can shorten detection time and provide reliable basis for noninvasive temperature estimation in practical application.
high intensity focused ultrasound;two-dimensional discrete Walsh transform;low-frequency component; noninvasive temperature measurement;subtraction image;curve fitting
1000-3428(2015)01-0227-04
A
TP391.41
10.3969/j.issn.1000-3428.2015.01.042
国家自然科学基金资助项目(11174077,11474090);湖南省自然科学基金资助项目(11JJ3079);湖南省教育厅基金资助项目(12C0237)。
李 勇(1989-),男,硕士研究生,主研方向:数字图像处理;丁亚军(通讯作者),副教授;钱盛友,教授、博士生导师;段先知,硕士研究生;邹 孝,讲师、硕士。
2014-03-05
2014-04-01 E-mail:448924457@qq.com
中文引用格式:李 勇,丁亚军,钱盛友,等.离散Walsh变换在超声治疗无损测温中的应用[J].计算机工程,2015, 41(1):227-230.
英文引用格式:Li Yong,Ding Yajun,Qian Shengyou,et al.Application of Noninvasive Temperature Measurement with Discrete Walsh Transform in Ultrasound Therapy[J].Computer Engineering,2015,41(1):227-230.

