基于提升小波变换的网络流量混合预测模型

邹 威,费金龙,祝跃飞,韩 冬

(1.数学工程与先进计算国家重点实验室,郑州450000;2.信息工程大学,郑州450000)

基于提升小波变换的网络流量混合预测模型

邹 威1,费金龙1,祝跃飞1,韩 冬2

(1.数学工程与先进计算国家重点实验室,郑州450000;2.信息工程大学,郑州450000)

当前流量预测模型难以准确刻画互联网流量的多重特性,并且存在构建时间长、预测精度低的问题。为此,设计基于提升小波分解的网络流量混合预测模型(WLGC)。该模型利用提升小波将流量时间序列快速分解为分别具有低频和高频特性的近似时间序列和细节时间序列,近似时间序列利用最小二乘支持向量机(LSSVM)预测并通过广义回归神经网络(GRNN)进行误差校准,细节时间序列在半软阈值降噪后利用自适应混沌预测方法对其预测,最后使用提升小波重构得到时间序列的预测值。仿真实验结果表明,该模型可有效提高预测精度。

流量预测;提升小波;最小二乘支持向量机;广义回归神经网络;阈值降噪;混沌预测

1 概述

随着互联网的迅速发展,网络规模日益扩大,网络应用日益多样化,形成了一个高度复杂的非线性非平稳系统。网络资源的优化配置、网络的安全性和可靠性如何保证为人们提出了新的挑战。对网络流量的准确分析以及精确高效预测是解决上述问题的有效手段。

网络流量具有多重特性,如非平稳、非线性、自相似性、长相关性、短相关性、多分形性、周期性、突发性、混沌性等。传统的流量预测模型难以准确刻画当前的网络流量特性,因此,越来越多的研究转向了非线性预测方法,如神经网络[1]、小波变换[2]、支持向量机[3]、混沌模型[4]等。神经网络具有优良的非线性处理能力,能够逼近任意的非线性网络,并且具备较强的自学习能力。但神经网络基于的是经验风险最小化准则,可能会导致过度拟合的现象,使得网络的泛化能力下降。为了避免出现过度拟合的现象,提高模型的泛化能力,Vapnic提出了结构风险最小化准则,基于结构风险最小化准则的支持向量机回归模型广泛应用于网络流量预测中[5]。最小二乘支持向量机[6](Least Squares Support Vector Machine, LSSVM)的出现避免了二次规划的求解问题,在节约计算资源的同时提高了求解速度。然而,由于网络流量时间序列中存在着突变和持续的强烈波动, LSSVM模型的预测误差仍有待进一步缩小。此外, LSSVM模型的参数往往根据经验确定,预测效果受到一定影响。另外,LSSVM模型无法准确刻画网络流量的混沌特性,因此,文献[7]提出了LSSVM模型和混沌预测模型相结合的方法,提高了预测精度。但该方法没有考虑流量高低频率的不同特性,并不能充分发挥LSSVM和混沌预测模型的预测能力,无法达到更高的预测精度。为此,基于具有多分辨率分析能力的传统小波变换将高度复杂相关的流量时间序列分解为彼此不相关的高频和低频2个部分,分别利用LSSVM模型和混沌模型预测的方法应运而生[8]。但是,传统小波基于傅里叶变换,分解和重构的计算量大、时空复杂度高,影响预测效率。而高频细节时间序列具有很强的混沌特性,信号中夹杂着的噪声噪声会破坏混沌吸引子的结构,导致预测不够准确。另外,文献[9]中,在小波分解成n层后,为尽量提高预测精度,对n+1个分量分别建模并预测。但在最终将预测值合成时,每一组的误差也被合成,可能会导致误差放大,影响预测精度。

针对上述问题,本文采用运算速度较快的提升小波变换算法[10]将原始时间序列分解为低频近似时间序列和高频细节时间序列。针对具有较强非线性特性的低频近似时间序列采用LSSVM模型预测,并利用速度快、非线性逼近能力强的广义回归神经网络[11](General Regression Neural Network,GRNN)对近似时间序列的预测误差进行预测,校准LSSVM模型的预测结果。针对高频细节时间序列,在单位根检验[12]后,将高频分量合成后,利用半软阈值降噪[13]的方法进行降噪,随后利用具有自学习能力的Volterra级数自适应混沌预测[14]算法进行预测。最后,对高频和低频序列的预测结果进行提升小波重构,得到最终的预测结果。

2 混合预测模型

2.1 构建原理

本文提出了一种基于提升小波分解的网络流量混合预测模型。模型的输入为原始流量时间序列Xt,输出为针对原始流量时间序列的预测值(PAt+Et′)⊕PDt。具体的混合预测模型框图如图1所示。

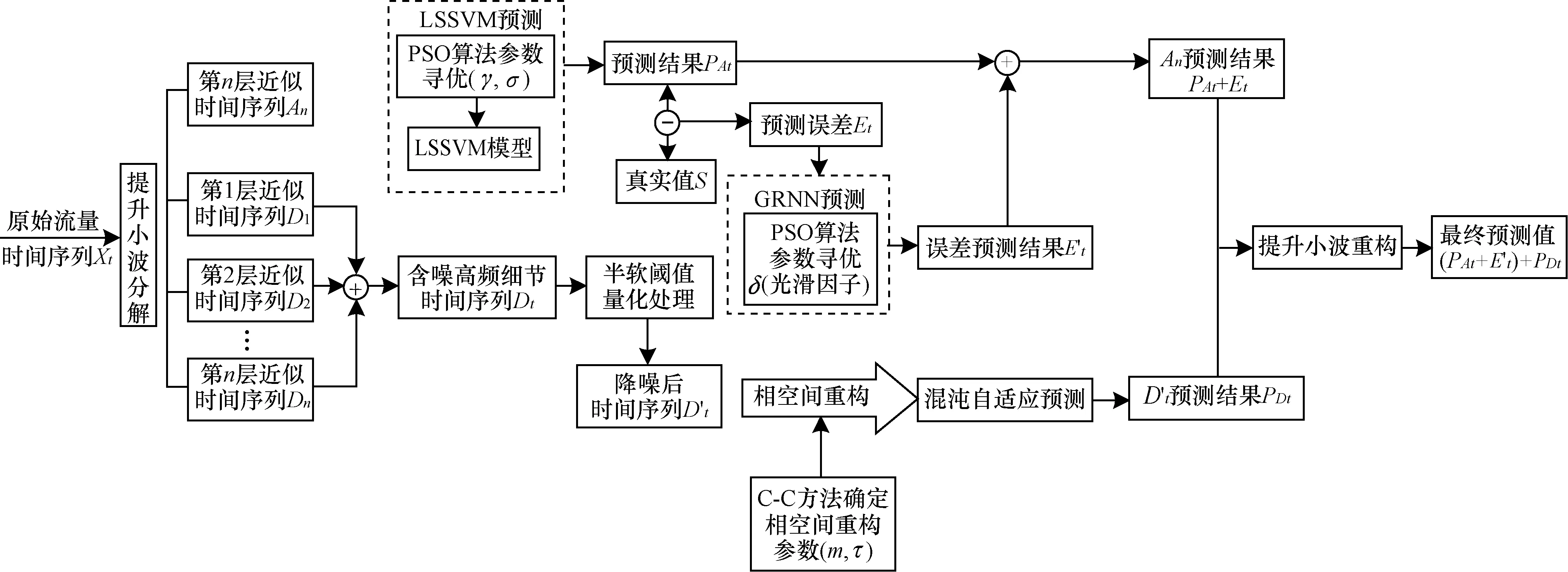
图1 混合预测模型

该模型首先根据“分而治之”的思想,利用提升小波分解,较快地将原始流量时间序列Xt分解为低频分量和高频分量。低频分量是一个比原始流量时间序列更加平滑的近似时间序列An(n为小波分解的层数),保留了原始流量时间序列中的基本特征分量,描述了网络流量长期演化趋势、周期性等较为确定的性质。高频分量为n个细节时间序列D1,D2,…,Dn,即为原始流量时间序列中蕴含的混沌信号以及噪声信号,显示的是网络流量的细节特征,描述了信号突变、瞬时的特性。

针对近似时间序列An,利用最小二乘支持向量机回归模型对其预测。LSSVM模型中涉及到的参数为惩罚因子γ以及径向基核函数的宽度σ。通过简单快速的粒子群优化算法[15]同时寻找最优的参数组合(γ,σ)以充分发挥LSSVM模型的逼近能力和泛化能力,得到预测值的序列PAt。随后,利用广义回归神经网络对LSSVM的预测误差序列Et进行预测(GRNN网络的光滑因子δ通过PSO优化算法确定),得到相应的预测值Et′,用来校准PAt,即最终预测值为PAt+Et′。

针对细节时间序列D1,D2,…,Dn,若对每个Di(i=1,2,…,n)分别建模并预测会消耗大量的时间,并且将每组预测结果合成的同时对误差也进行了合成,会导致误差的放大,影响预测精度。故考虑将Di进行合并后再进行建模预测。首先对Di进行单位根检验,经检验发现,高频序列基本都是平稳的。由于对平稳序列做代数运算不会改变其平稳性,因此对这些频谱相近的高频细节时间序列进行合并,以达到减少子序列的目的,同时避免了对每组分量分别建模预测带来的误差放大问题。对合并后的含噪细节时间序列Dt进行半软阈值降噪得到了Dt′,保留了Dt的特征,并且信号较为平滑,降噪效果好。随后用C-C方法同时确定相空间的嵌入维数m和延迟时间τ以便进行相空间重构[16],基于重构的相空间,采用Volterra级数自适应混沌预测方法对其预测,得到预测值PDt。

最后,将PAt+Et′和PDt进行提升小波重构,得到原始时间序列Xt的预测值(PAt+Et′)⊕PDt。

2.2 模型参数确定

为使上述模型的预测效果达到最佳,其相关参数的确定至关重要。提升小波分解中小波函数的选取和分解层数的确定,LSSVM模型中惩罚因子γ和径向基核函数宽度σ的确定,以及GRNN网络中光滑因子δ的确定,均为混合预测模型中需解决的关键问题。

(1)小波函数的选取

针对以下4种常用的小波函数进行比较分析(Haar,db3,coifl,sym3),选取一个最佳的小波函数。关键是分析判断该小波函数是否能刻画出原始流量的统计特征,结合网络流量的特性,主要是长相关性和多分形性。而Haar小波函数在刻画流量的长相关性和多分形性上比其他3个小波函数的性能要好。

(2)分解层数的确定

分解层数越大,所能观察到的网络流量细节特征就越多;反之,所能观察到的细节特征就越少。但当分解层数过大时,分解的计算量也会迅速加大,不便于预测。因此,小波分解的层数不宜过大,也不宜过小。一般地,小波分解10层之后,预测误差会趋于稳定。另外,分解层数为3的时候,预测误差基本可达到预期目的。因此本文将利用Haar小波函数对原始流量时间序列Xt进行3层提升小波分解,分解为一个近似时间序列A3和3个细节时间序列D1,D2,D3。

(3)惩罚因子和径向基核函数宽度(γ,σ)的寻优

在LSSVM模型中,惩罚因子γ和径向基核函数的宽度σ对模型的预测精度和泛化能力起着关键作用。γ能够在训练误差和模型复杂度之间取折中值,使函数具有较好的泛化能力。γ过小,训练误差变大,模型复杂度降低;γ过大,训练误差减小,模型复杂度提高,泛化能力变差。σ反映了支持向量之间的相关程度。σ过小,支持向量之间的相关性较差,回归模型相对复杂,泛化能力得不到保证;σ过大,支持向量之间的相关性过大,回归模型难以达到预期的精度。由此可见,LSSVM模型的预测精度和泛化能力取决于γ和σ,特别是它们之间的相互影响。因此,在参数选择时应该综合考虑这两个参数形成的参数对(γ,σ)。

参数选择的本质是一个优化搜索过程,因此,本文采用概念简单、效率高、容易实现的粒子群优化算法对参数对(γ,σ)寻优,具体的寻优过程如图2所示。

图2 基于PSO的LSSVM参数寻优过程

PSO优化LSSVM模型参数对(γ,σ)的具体步骤如下[15]:

Setp 1确定参数对(γ,σ)的搜索范围,对PSO的参数进行设置,随机初始化每一个粒子的速度和位置。

Setp 2计算所有粒子的适应度值,适应度函数选为能直接反应模型回归性能的均方百分比误差:

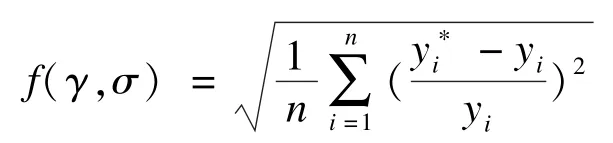
Setp 3 对每个粒子,将其适应度值与个体极值pbest进行比较,若小于pbest,则更新pbest。

Setp 4 对每个粒子,将其个体极值pbest与全局极值gbest进行比较,若小于pbest,则更新pbest。

Setp 5 根据速度和位置的更新公式,对粒子的速度和位置进行更新。

Setp 6 若未达到终止条件,则转Step2;否则,输出最佳参数对(γ∗,σ∗)。

(4)光滑因子δ的寻优

在GRNN网络中光滑因子δ的值对网络性能影响很大,若δ非常大,预测值则近似于所有样本因变量的平均值;若δ趋近于0,则预测值与训练样本的值非常接近,当需要预测的点在训练样本中时,预测值与样本中的期望输出非常接近。但一旦接收一个新的输入,预测效果就会急剧变差,网络失去泛化能力,即出现了过学习现象。因此,采用PSO算法寻找一个合适的光滑因子值,确保网络的预测精度以及泛化能力,适应度函数选为均方百分比误差:

3 混合预测算法

根据上节提出的混合预测模型,本文提出了一种混合预测算法。表1中给出了该算法以及各子算法的功能描述。

表1 算法及各子算法的功能描述

整个混合预测算法的伪代码描述如下:

算法Program HybridPredict

输入O_Time_S是原始网络流量时间序列

输出H_Predict_R是O_Time_S的最终预测结果

上述混合预测算法HybridPredict共调用4个子算法,分别是LSSVR,GRNNP,P_Respective_Chaos和P_Compose_Chaos,完成了对原始网络流量时间序列的预测。

具体来说,整个算法的第2行对输入的流量时间序列O_Time_S进行3层提升小波分解,分解速度快、存储单元利用少、时空复杂度低,很好地解决了基于傅里叶变换的传统小波分解效率不高的问题。第3行调用LSSVR子算法,利用最小二乘支持向量机回归模型对近似时间序列A_Time_S进行预测,得到预测结果以及均方误差,避免了标准支持向量机复杂的求解二次规划问题。第 4行调用GRNNP子算法,对近似时间序列的误差序列进行预测,用于第5行的误差校准,可进一步解决流量时间序列中存在的突变和持续强烈波动带来的预测精度下降的问题。由于GRNN网络不需要训练,因此利用该网络进行误差校准不会导致预测时间成本大幅上升。第6行～第8行对3个细节时间序列D1,D2和D3进行单位根检验。第9行～第17行首先判断3个细节时间序列是否都为平稳时间序列,如果不都是平稳的,则调用P_Respective_Chaos子算法对3个序列利用自适应混沌模型分别预测。利用提升小波重构算法得到最终的预测结果H_Predict_R;如果都是平稳的,则将3个细节时间序列合并后,调用P_ Compose_Chaos子算法利用自适应混沌模型进行预测,利用提升小波重构算法得到最终预测结果H_ Predict_R,减少了预测序列的个数,进而降低了针对多个子序列分别建模预测的时空代价,同时避免了对各子序列预测结果合并带来的误差放大的问题。

4 预测实例

预测实例所采用的网络流量数据来自于新西兰某ISP[17],公开了2009年1月6日16:00:00—1月16日10:00:00的数据,统计间隔时间为30 min,共采集到470个实验数据,形成了一个原始网络流量时间序列,如图3所示。

图3 原始网络流量时间序列

4.1 仿真实验过程

实验选取前430个数据作为训练集,后40个数据作为测试集。整个仿真过程通过Matlab软件完成。首先利用Haar小波对原始流量时间序列进行3层提升小波分解,分解后得到近似时间序列A3与细节时间序列D1～D3,如图4所示。

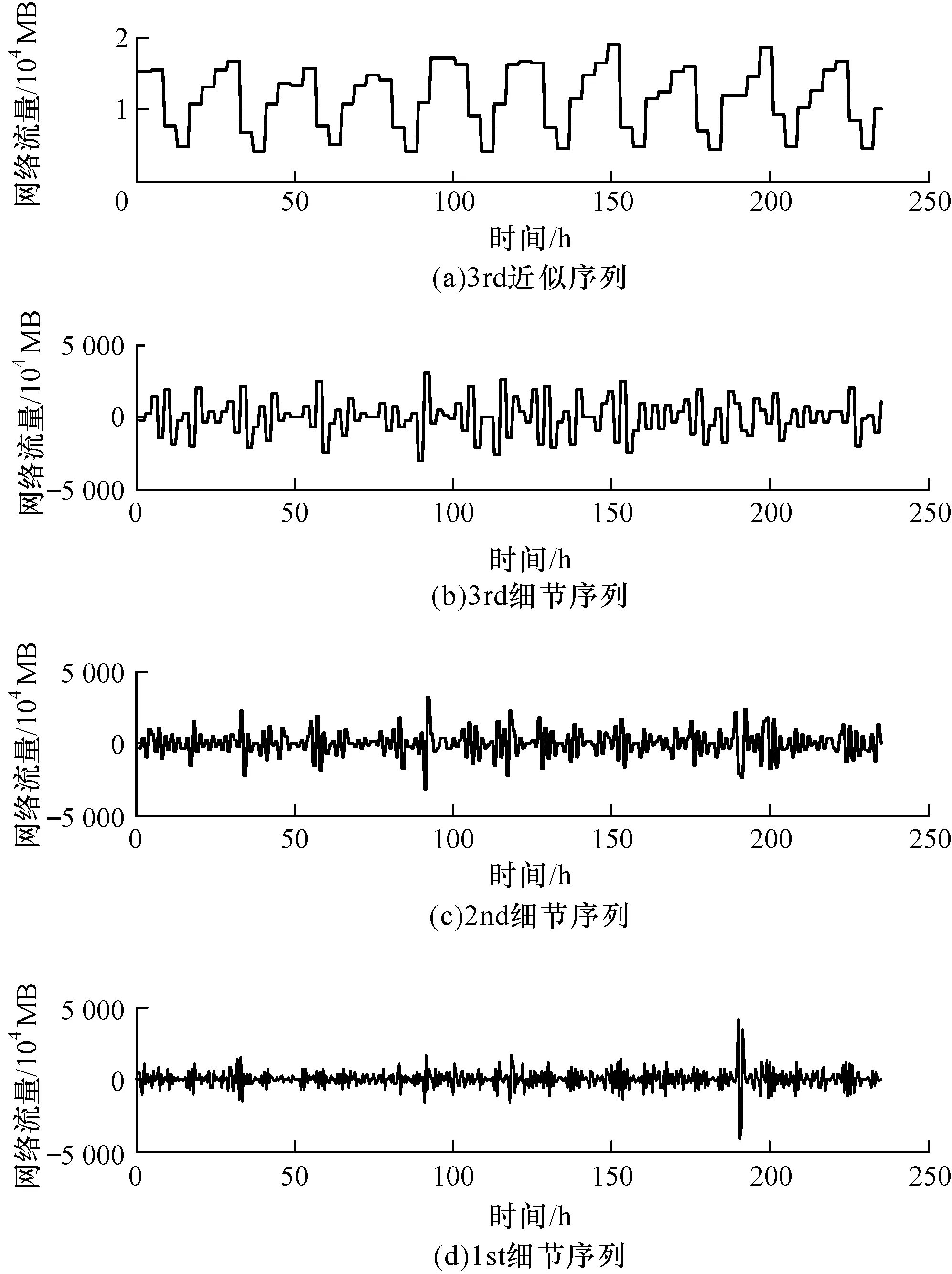
图4 原始流量时间序列的提升小波分解

由图4可以看出,第3层近似时间序列相对原始流量时间序列更加平滑,很好地保留原始时间序列的整体趋势。针对该近似时间序列,采用最小二乘支持向量机回归模型进行预测,得到预测结果以及均方误差。模型中涉及到的惩罚因子γ和径向基核函数的宽度σ由PSO算法确定,其中,PSO算法的初始参数设置如下:加速度常数C1=1.5,C2=1.7,惯性权重w=2,γ∈(0.01,1 000),σ∈(0.1,100),种群个数为20,最大迭代次数为200。适应度函数选为能直接反应模型回归性能的均方百分比误差:

对于3个细节时间序列,Di(i=1,2,3),经过单位根检验,发现均为平稳序列,故将其合并为Dt高频信号中主要是混沌信号和与其部分重叠的噪声信号,由于噪声信号会破坏混沌吸引子的结构,影响利用混沌模型进行预测的预测精度。由于半软阈值降噪方法兼顾了硬阈值和软阈值的优点,在阶跃跳变处和光滑处的降噪效果都比较理想,故采用半软阈值量化的方法对Dt进行降噪处理。图5给出了降噪前的Dt和降噪后的Dt′。

图5 合并的细节信号去噪

随后,根据C-C方法得到相空间的嵌入维数m和延迟时间τ分别为6和4,基于重构的相空间采用自适应混沌预测法对降噪后的Dt′进行预测。

最后,对近似时间信号的最终预测值和降噪后的细节信号Dt′的预测值,利用提升小波逆变换进行提升小波重构,得到最终的预测值。

4.2 仿真实验结果及分析

图6给出了本文提出的预测方法与常用方法(混沌预测法[18]、LSSVM 法[6]和混沌 LSSVM法[7])之间的预测值对比曲线。文献[18]将网络流量时间序列看作是混沌时间序列,故采用混沌模型进行预测。从图6中可看出,单一利用混沌模型对流量时间序列进行预测的预测效果并不理想,原因是混沌系统具有初值敏感性,不具备长期可预测性,故后面的时刻预测效果尤为不佳。图6中亦可看出只通过最小二乘支持向量机模型进行流量数据的预测,整体的预测效果较好,但无法准确预测真实流量的突变和持续的强烈波动。文献[7]基于重构的相空间,利用最小二乘支持向量机进行预测。由于相空间重构将原始流量时间序列的维数扩展到更高的维度,把时间序列中蕴藏的信息充分显露出来,为预测提供了更多的信息,因此,图6可见其预测精度高于前两种方法。但由于该方法没有分别针对高频和低频信号进行预测,针对性不强,预测精度仍有待进一步提高。显然,较上述3种常用方法,本文提出的预测方法可以得到与真实的网络流量数据最为接近的预测值,预测效果最佳。

图6 不同模型的预测曲线对比

本文采用均方百分比误差(MSPE)作为评价模型整体预测效果的指标:

表2给出了上述几种预测方法的预测误差对比数据。可见本文提出的预测方法具有最低的预测误差,因此,同样可以看出该方法的预测精度最高。

表2 预测误差比较

上述实验通过预测曲线以及预测误差对比,初步、直观地验证了WLGC模型的有效性。下面采用残差序列白噪声检验法[19],从理论上验证该模型的有效性。

由于序列值之间的变异性是绝对的,而相关性是偶然的,因此给出如下假设条件。

原假设:延迟期数小于或等于m期的序列值之间相互独立(m为指定延迟期数)。

备择假设:延迟期数小于或等于m期的序列值之间有相关性。

该假设条件用数学语言描述即为:

其中,ρ为自相关系数。

由于本例对40个实验数据进行残差检验,属于小样本情况,因此采用LB统计量进行检验。表3为残差序列20期样本的自相关系数。

表3 残差序列20期样本的自相关系数

根据上述数据,很容易得到表4的结果,可以看出,P值显著大于显著性水平α(α=0.05)(P表示原假设成立的可能性即概率)。所以该序列不能拒绝原假设。换言之,可以认为该序列的波动没有任何统计规律可循,即已经没有可以识别的信息。因此,该残差序列可以认为是白噪声序列,表明WLGC模型达到了较高的预测精度,验证了该模型的有效性。

表4 LB统计量检验结果

5 结束语

本文提出了一种基于提升小波分解的混合预测模型WLGC。利用基于傅里叶变换的提升小波变换快速地将原始网络流量时间序列分解为低频的近似时间序列和高频的细节时间序列。对低频信号,利用LSSVM回归模型对其预测,进一步采用GRNN网络校准误差。对高频信号,利用具有自学习能力的自适应混沌预测方法对其预测,通过提升小波重构算法得到最终预测值。仿真结果表明,与单一利用LSSVM、混沌模型或LSSVM-Chaos模型相比,本文模型的数据拟合效果和模型预测精度更好。

[1] Hodge V,Krishnan R,Jackson T,et al.Short-term Traffic Prediction Using a Binary Neural Network[C]// Proceedings of the 43rd Annual UTSG Conference. Milton Keynes,UK:Open University,2011.

[2] Wei Yongtao,Wang Jinkuan,Wang Cuirong.Network Traffic Prediction Based on Wavelet Transform and Season ARIMA Model[C]//Proceedings of ISNN’11. Berlin,Germany:Springer-Verlag,2011:152-159.

[3] Li Lingli,Xia Hongxia,Li Lin,et al.Traffic Prediction Based on SVM Training Sample Divided by Time[J]. TELKOMNIKA Indonesian Journal of Electrical Engineering,2013,11(12):7446-7452.

[4] Fu Yinping,WeiWei.ResearchontheShort-term Traffic Flow Forecasting Method Based on Chaos Theory[C]//Proceedings of ICTE’13.Chengdu,China, [s.n.],2013:2637-2642.

[5] Cortes C,Vapnik V.Support-vector Networks[J]. Machine Learning,1995,20(3):273-297.

[6] Suykens J A K,Vandewalle J.Least Squares Support Vector Machine Classifiers[J].NeuralProcessing Letters,1999,9(3):293-300.

[7] Liang Ximing,Yan Gang,Li Shanchun,et al.Nonlinear Predictive Control Based on Least Squares Support Vector Machines and Chaos Optimization[J].Information and Control,2010,39(2):129-135.

[8] Feng Xiangrong.Traffic Prediction Scheme Based on Chaotic Models in Wireless Networks[J].Journal of Networks,2013,8(9):2101-2106.

[9] 麻书钦,范海峰.基于小波变换和时间序列的网络流量预测模型[J].河南理工大学学报:自然科学版, 2013,32(2):188-192.

[10] 张 军,成礼智,杨海滨,等.基于纹理的自适应提升小波变换图像压缩[J].计算机学报,2010,33(1):184-192.

[11] Luo Wei,Fu Zhuo.Application of Generalized Regression Neural Network to the Agricultural Machinery Demand Forecasting[J].Applied Mechanics and Materials,2013, 278-280:2177-2182.

[12] 靳庭良.DF单位根检验的势及检验式的选择[J].统计与决策,2005,(5X):13-17.

[13] Chen Feng,Zhang Wenwen,Chen Qian,etal. Application ofWaveletSemi-softThreshold Filter Algorithm in EMCCD’s Image Processing[C]// Proceedings of OIT’13.Beijing,China:International Society for Optics and Photonics,2013.

[14] 张玉梅,马 骕.交通流序列的 Volterra自适应预测[J].计算机工程,2011,37(16):185-187.

[15] Trelea I C.The Particle Swarm Optimization Algorithm: Convergence Analysis and Parameter Selection[J]. Information Processing Letters,2003,85(6):317-325.

[16] 王海燕,盛昭瀚.混沌时间序列相空间重构参数的选取方法[J].东南大学学报:自然科学版,2000,30(5): 113-117.

[17] WAND Network Research Group.Waikato Internet Traffic Storage[EB/OL].[2014-01-10].http://wand.net.nz/ wits/ispdsl/1/.

[18] Yin A,Zhang S,Qi J.The Research on Network Traffic Modeling Based on Chaotic Time Series[J].Journal of Computational Information Systems,2012,8(8):3323-3330.

[19] Woodward W A,Gray H L,Elliot A C.Applied Time Series Analysis[M].[S.l.]:CRC Press:2011.

编辑 金胡考

Hybrid Prediction Model of Network Traffic Based on Lifting Wavelet Transform

ZOU Wei1,FEI Jinlong1,ZHU Yuefei1,HAN Dong2
(1.State Key Laboratory of Mathematical Engineering and Advanced Computing,Zhengzhou 450000,China; 2.Information Engineering University,Zhengzhou 450000,China)

Current traffic prediction models can not accurately depict the multi-properties of network traffic.Apart from this,model construction is time-consuming and prediction accuracy is low.To address the problem,a lifting-wavelet-based hybrid prediction model for network traffic called WLGC is proposed.In WLGC model,a lifting wavelet is adopted to quickly decompose traffic time series into low-frequency approximate time series and high-frequency detailed time series. Least Squares Support Vector Machine(LSSVM)is leveraged to predict the approximate time series and General Regression Neural Network(GRNN)is leveraged to calibrate the prediction error.The adaptive chaotic prediction method is used to predict the detailed time series after the semi-soft threshold denoising.Finally,the inverse lifting wavelet transform is performed to get the predicted values of the original time series.Simulation results verify the validity of the proposed method and the prediction accuracy is increased compared with current prediction methods.

traffic prediction;lifting wavelet;Least Squares Support Vector Machine(LSSVM);General Regression Neural Network(GRNN);threshold denoising;chaotic prediction

1000-3428(2015)01-0024-07

A

TP18

10.3969/j.issn.1000-3428.2015.01.005

国家自然科学基金资助项目(61309007);郑州市科技创新团队基金资助项目(10CXTD150)。

邹 威(1988-),男,硕士研究生,主研方向:信息安全;费金龙,讲师;祝跃飞,教授、博士生导师;韩 冬,讲师。

2014-02-20

2014-03-20 E-mail:zouwei1214@126.com

中文引用格式:邹 威,费金龙,祝跃飞,等.基于提升小波变换的网络流量混合预测模型[J].计算机工程,2015, 41(1):24-30.

英文引用格式:Zou Wei,Fei Jinlong,Zhu Yuefei,et al.Hybrid Prediction Model of Network Traffic Based on Lifting Wavelet Transform[J].Computer Engineering,2015,41(1):24-30.