基于Prim最小生成树的路面裂缝连接算法

任 亮,徐志刚,赵祥模,周经美

(长安大学信息工程学院,西安710064)

基于Prim最小生成树的路面裂缝连接算法

任 亮,徐志刚,赵祥模,周经美

(长安大学信息工程学院,西安710064)

在利用数字图像技术检测路面裂缝时,由于部分裂缝过窄或被阴影遮挡或被灰尘填充,导致检测出的裂缝目标不连续,严重影响后续的裂缝参数测量和评价。为此,提出一种基于Prim最小生成树的路面裂缝连接算法。利用屋脊边缘检测方法识别所有的可疑裂缝目标,运用裂缝形状特征去除斑点或块状噪声,实现裂缝的粗定位。在此基础上,通过形态学方法提取粗定位裂缝片段的端点,利用Prim算法构造最小生成树实现路面裂缝片段端点的连接,同时使用裂缝的方向和对比度特征去除连接中的强制伪连接;在连接的基础上对裂缝进行填充和增强,得到完整的裂缝分割目标。对200幅路面图像进行算法测试,应用Hausdorff距离对多种算法的分割性能进行评估,实验结果表明,该算法能明显提高裂缝检测目标的连续性,其检测准确率比灰度直方图等算法高出6个～13个百分点。

交通工程;路面养护;裂缝检测;Prim最小生成树;裂缝连接;Hausdorff距离

1 概述

截至2012年底我国高速公路总里程达9.56万公里,随着高速公路通车时间的增长,路面破损养护问题逐渐凸显出来。路面破损检测是路面破损养护的重要环节,能为道路资产信息管理、道路设施和道路性能评估、道路寿命预测等提供有力数据支持,对道路养护至关重要[1]。自20世纪80年代以来,欧美等发达国家将现代光学技术和计算机技术相结合,先后开发了基于激光测距和数字图像处理的多功能检测车[2],这种检测车具有检测效率高、人为因素少、不影响交通的优点,在路面检测中得到了越来越多的应用,我国在这方面虽起步较晚,但是发展迅速,目前已接近世界先进水平。由于路面裂缝检测算法还不够成熟,现有的路面自动检测系统很大程度上还是采用自动采集与人工识别的方式进行工作。由于路面图像数量巨大,人工检测效率,检测结果客观性差,开发全自动的高性能路面裂缝识别算法仍然迫在眉睫。

文献[3]指出路面损坏状况指数(PCI)是评价路面损坏程度的重要指标,其主要由沥青路面破损率(DR)得出。而路面裂缝的种类、面积、长宽等参数直接影响沥青路面破损率的计算。国内外相关领域的学者对基于图像的路面裂缝自动检测算法进行了广泛的研究,多种裂缝检测算法和理论[4]相继被提出。目前的研究算法主要分为4类:(1)基于边缘检测的方法[5];(2)基于灰度统计的方法[6];(3)基于分块分析的方法[7];(4)基于几何分析的方法[8];这些算法也对部分裂缝取得了较好的检测效果。然而这些方法没有对路面裂缝进行连接,并未表达出真实的裂缝的完整骨架结构[9]。路面裂缝连接算法对路面裂缝进行连接使得裂缝更加完整、连续,从而使得出的裂缝参数更加准确,进而能更加客观地评价路面破损程度。文献[10]针对路面裂缝对比度低、连续性差等特点,提出了利用目标点最小生成树的路面裂缝检测,但其对大尺度、互相邻近及交叉的复杂裂缝(龟裂)效果不理想。

2 本文多功能道路检测系统

本文在前人研究的基础上,提出一种基于Prim最小生成树的路面裂缝连接算法。该算法首先对路面裂缝进行屋脊边缘检测,并用裂缝特征去除检测后的干扰,实现裂缝粗定位;然后用图论中的最小生成树来表达粗定位后裂缝骨架之间的连续性,对裂缝使用Prim算法构造最小生成树实现路面裂缝的连接,同时使用裂缝特征去除连接中的强制错误连接;最后在连接的基础上对裂缝进行填充和增强。

本文采用如图1所示的自主开发道路综合信息采集车来获取路面图像,在该系统中,摄像机光轴方向垂直路面,其分辨率为4 096×1 024像素,覆盖宽度为一个车道(约4 m),长度为1 m,为了便于后期处理,本文将其分割为4幅分辨率为1 024×1 024像素的图像,每个像素约代表1 mm2的路面。

图1 多功能道路检测车示意图

3 路面裂缝的粗定位

3.1 基于屋脊边缘的路面裂缝检测

沥青路面裂缝边缘为屋脊边缘,屋脊边缘的极值点位置与其剖面上一维信号的一阶导数零点和二阶导数极值点对应[11]。高斯函数对一维信号做卷积运算,相当于对该信号做高斯滤波,高斯函数的一阶导数和二阶导数与一维信号进行卷积相当于该信号的一阶导数和二阶导数与高斯函数进行卷积,高斯导数滤波器示意图如图2所示。

图2 高斯导数滤波器示意图

然后用构造的滤波器分别与路面图像的每行和每列进行卷积,通过每行和每列的一阶导数零点和二阶导数强度及像素点的灰度值选出屋脊边缘极值点。然后对筛选出的行屋脊边缘极值点图像和列屋脊边缘极值点图像进行叠加,求出路面裂缝屋脊边缘极值点图像,如图3所示。

图3 路面裂缝屋脊边缘检测

3.2 基于形状特征和形态学的裂缝噪声去除

形态学去除噪声过程如图4所示。路面裂缝屋脊边缘极值点图像中仍存在大量的噪声,如图4(a)所示,产生噪声的主要原因是由于这些噪声在局部也是屋脊边缘,而被检测为裂缝目标。从图4(a)中可以看出,裂缝主体已被检测出来,同时伴有大量的噪声,但噪声不是很集中,因此可以根据裂缝表现出的线状特征和方向性将两者区分开[12]。本文根据裂缝的连通域属性和形状属性选取了以下5个特征因子:

(1)连通域的方向:指二值化裂缝后连通域最小外接椭圆的长轴方向;

(2)连通域的长度:指二值化裂缝后连通域最小外接椭圆的长轴长;

(3)连通域的面积:指二值化裂缝后连通域中的像素个数;

(4)连通域的线性度:指二值化裂缝后连通域最小外接椭圆长轴L与短轴值l之比;

(5)连通域的连续性:取二值化裂缝后连通域T的最小外接矩形,以该矩形为中心,做该矩形八邻域方向的8个大小一样的矩形,统计这8个矩形区域中的其他连通域像素的个数M,当M小于置阈值TH时,则认为裂缝是孤立的不连续的。

由于裂缝局部不连续,因此采用膨胀的方法将局部裂缝连接起来,并对膨胀后的裂缝进行联通域标记,结合裂缝特征因子,去除干扰,实现裂缝的粗定位,如图4(d)所示。然而,粗定位后的裂缝连续性差且是零碎、不完整的,因而需要对裂缝进行连接。

图4 形态学去除噪声过程

4 路面裂缝的连接

由于裂缝过细、缝壁脱落积灰、拍摄时光线强度和方向等因素影响,裂缝只在宏观上呈现为连续,因此去除干扰后得到的是裂缝的零碎片段。图论提供了对事物及其之间关系进行描述、分析和处理的完整理论和方法。用图来描述粗定位后裂缝零碎片段的空间分布,将方便对其进行全局分析和操作。分析裂缝的成像条件和裂缝的特征,本文采用最小生成树表现零碎裂缝片段间的连续性。根据裂缝的连续性,将零碎片段连接起来获得完整的裂缝。

4.1 Prim最小生成树原理

Prim最小生成树是从一个具有n个顶点的带权无向完全图中选择n-1条边并使这个图连通,同时使生成树的权值最小。Prim算法从图中的一个顶点开始,把这个顶点包含在一个集合中,反复寻找一个顶点已在该集合中而另一个顶点还不在该集合中的最小权边,把新边和新结点归并到生成树中,如图5(a);本文中将零碎片段裂缝看作一个单元,计算各单元之间的距离,按最小距离选择边和归并单元;对于线段裂缝单元,其只有2个端点,且这2个端点不能相连,因此只搜索本端点到其他单元端点之间的距离,按最小距离选择边,归并连接单元的2个端点,如图5(b);然而对于分叉裂缝单元,其有多个端点,如图5(c),因此,需要将分叉裂缝单元分解为线段裂缝单元,如图5(d),然后按线段裂缝单元方法进行处理,如图5(e)。本文对粗定位后的零碎片段裂缝进行分解并提取端点,使用Prim算法构造最小生成树,并利用裂缝特征改造最小生成树实现裂缝的连接。

图5 Prim最小生成树示意图

4.2 端点提取

局部裂缝片段并非都是线段单元,因此需要对这些片段进行分解。首先对去除干扰后的裂缝图像取骨架,并对骨架进行细化处理,去除冗余像素,使其转化为8联通情况下的严格细化;然后去除其中3个及3个以上的交叉点,使其分解成为线性片段;最后对去除交叉点后的局部细化裂缝单元做这些单元的最小外接矩形,取局部细化裂缝单元与矩形的交点作为该细化裂缝单元的端点,如图6所示。

图6 端点提取过程

4.3 基于Prim算法的最小生成树连接

对所有的局部裂缝取端点得端点集合{T1,T2,…,Ti}。对得到的端点集合{T1,T2,…,Ti},构造特殊邻接矩阵L,该矩阵定义为:

其中,dis(Ti,Tj)为端点Ti到端点Tj的像素距离。

通过Prim算法构造最小生成树:记G=＜V,E＞是取端点后裂缝图像的一个联通的带权图,V即为已得到的端点集{T1,T2,…,Ti},E为边集,通过邻接矩阵得到。

(1)初始状态为:U={u1,u2}V={v1,v2,…},TE={}。其中,u1,u2为取端点后裂缝图像中最长局部细化裂缝单元的2个端点,v1,v2为端点集中的端点。

(2)在所有u∈U,v∈V-U的边(u,v)∈E中找一条权值最小的边(u0,v0),将这条边加进集合TH中,同时将此边的另一顶点v0及和v0属于同一裂缝的另一点v1并入U。

(3)如果U=V,则该算法结束;否则重复步骤(2)。

算法结束时,TH中包含了G中的n/2-1条边。经过上述步骤选取到的所有边恰好就构成了图G的一颗最小生成树。对图3(d)中的裂缝构造最小生成树,并对该图中的裂缝进行连接。

4.4 改造的最小生成树连接

裂缝的最小生成树连接是把所有的裂缝按最短路径相连,裂缝连接的同时把伪裂缝也连接上,如图7(a)所示,因此,需要对Prim算法构造的最小生成树中的边进行删选。由于交叉点之间形成的边本来是已经检测出的区域,因此只对非交叉点之间的边进行删选;对于非交叉点之间的边,按下式进行删除:

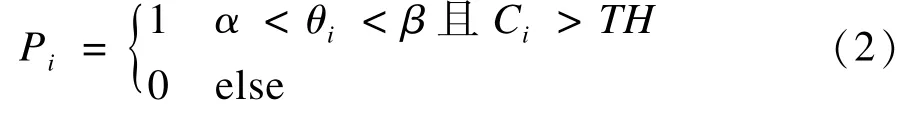
其中,θi为边i的角度;α,β分别为与边i相连的两条线状裂缝的角度;Ci为边i所在区域的对比度;TH为对比度阈值;若Pi为1则保留该边,否则删去该边。然后更新边集E,生成新的最小生成树,新的最小生成树去除了那些非裂缝区域的连接,如图7(b)所示。对于那些未连接的伪裂缝,按裂缝特征因子去除,如图7(c)所示。

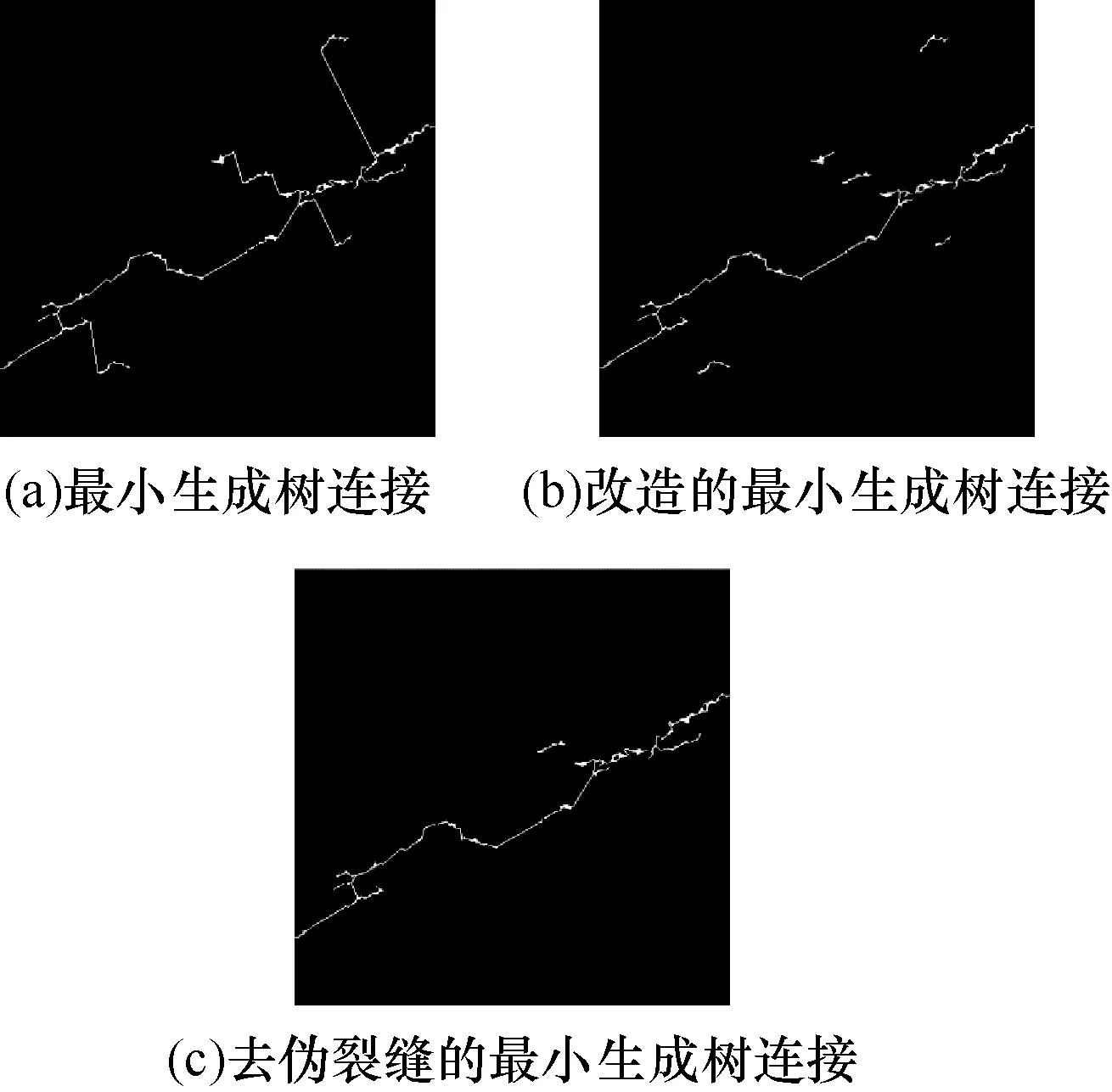
图7 基于改进Prim算法的裂缝连接图

5 裂缝的填充与增强

由于最小生成树连接为线段连接,而线段连接与实际的裂缝结构有一定差异,为了使连接区域更接近实际裂缝,去除错误的强制连接,本文对强制连接的线段采用其所在区域的灰度特征进行检验,具体过程如下:

(1)计算线段的邻域范围,其定义为到这条线段上的像素距离小于阈值L的区域,如图8所示。

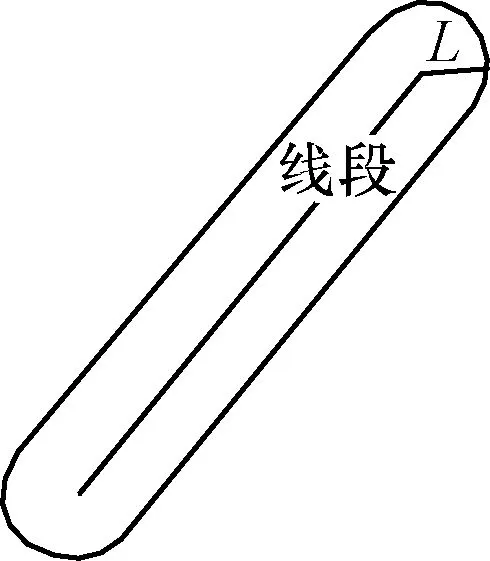
图8 线段的邻域图

(2)采用P分位数法对邻域内的像素进行二值化:对邻域内的像素按灰度值进行排序,对于序列中某点xp,当小于xp的灰度值个数占总个数的15%时,取点xp的灰度值为阈值,对邻域中的像素进行二值化。

(3)对二值化后的邻域进行联通域标记,使用裂缝的特征因子计算各连通域的线性度,保留线性度大于M的目标。

对图7(c)进行填充和增强,结果如图9所示。

图9 填充后的最小生成树连接

6 实验结果及分析

本文算法程序基于matlab7.8开发,运行环境为WindowsXP,CPU为Intel(R)core(TM)3.10 GHz,内存3.29 GB。为了测试本文算法的检测效果,对200幅路面图像进行了算法测试,并与其他算法(迭代裁剪法、种子修正法、灰度直方图法)进行实验对比。其中,图2中的5幅图像的测试结果如图10～图14所示。

图10 横缝识别结果

图11 纵缝识别结果

图12 细缝识别结果

图13 粗缝识别结果

图14 龟裂识别结果

为了有效评估裂缝检测的效果,采用文献[13]中的基于缓冲的 Hausdorff距离的分值测量方法。Hausdorff距离是描述2组点集之间相似程度的一种量度,它是2个点集之间距离的一种定义形式:假设有2组集合A={a1,a2,…,ai},B={b1,b2,…,bi},则这2个点集合之间的Hausdorff距离定义为:

其中,mamb分别为A,B集合中点的个数。由式(3)知,双向Hausdorff距离H(A,B)是单向距离h(A,B)和h(B,A)两者中的较大者,它度量了2个点集间的最大不匹配程度。将检测后的路面裂缝看做一个点集,两裂缝之间的Hausdorff距离是通过裂缝像素点在图像中的坐标进行计算。如图15所示,对于图15(a)中的裂缝中的点a,它与图15(b)中裂缝的最短距离点为点b。

图15 裂缝的Hausdorff距离示意图

在本文中BH(A,B)为人工裂缝分割图像和其他算法裂缝分割图像之间的距离,A和B分别对应人工裂缝分割图像和其他算法裂缝分割图像中裂缝位置的集合,其分值计算如下:

ScoringMeasure=100-BH(A,B)×100(6)

将各个算法检测的结果与人工分割的裂缝图像作比较,计算分值。表1和图16给出本文算法与3种经典算法的性能对比,结果表明,本文的识别结果比其他3种算法的检测均值高出6个～13个百分点,其对复杂裂缝(图13、图14)的检测结果值明显高于其他算法。

表1 4种算法识别得分对比

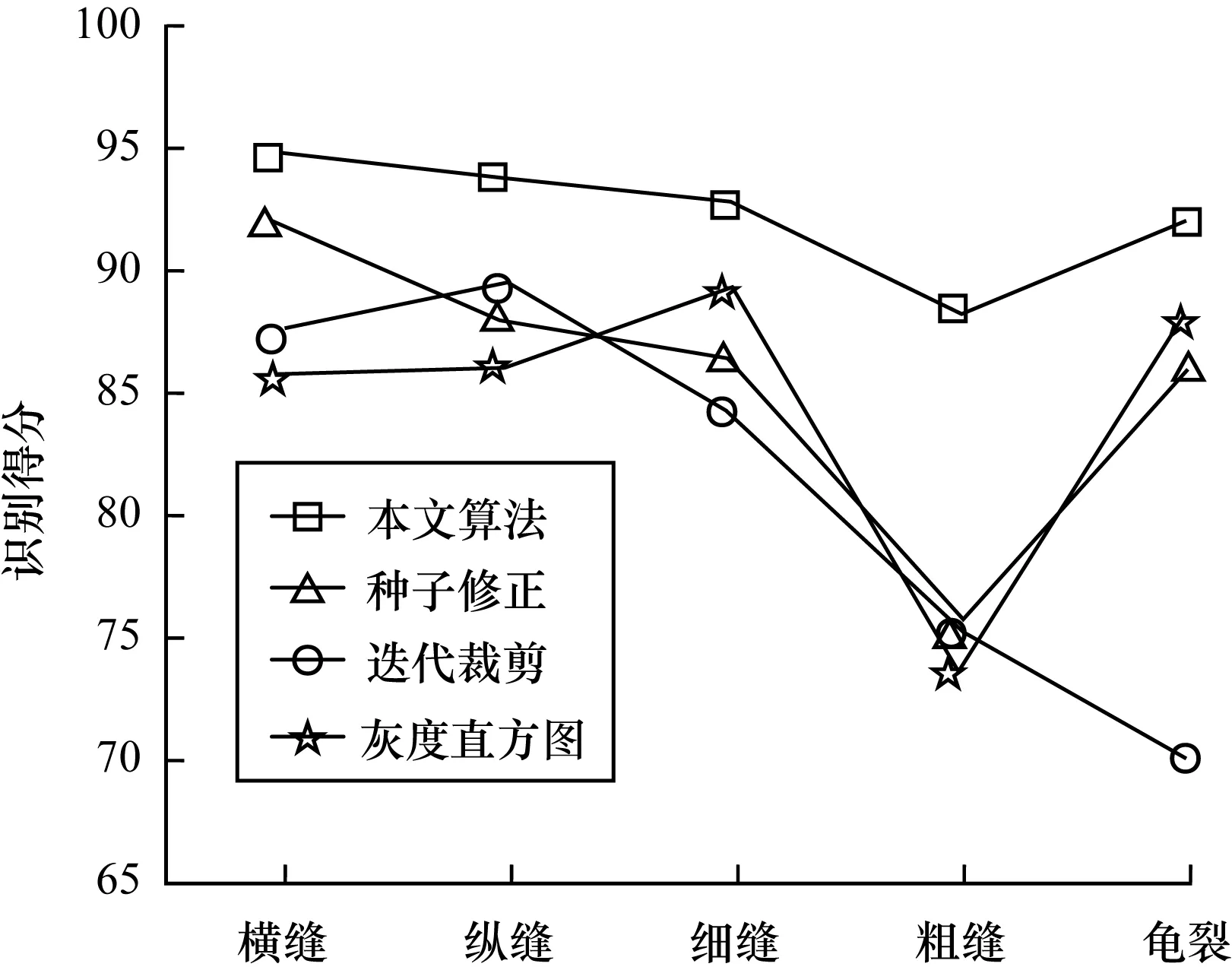
图16 4种算法识别得分对比

7 结束语

本文提出一种基于Prim最小生成树的路面裂缝连接算法,并通过研究得出以下结论:

(1)利用路面裂缝的屋脊边缘特征对裂缝进行屋脊边缘检测,使用路面裂缝形状特征因子去除检测后的噪声,可以实现裂缝的粗定位。

(2)利用最小生成树来表达粗定位后裂缝骨架之间的连续性,可以方便对其进行全局分析和操作。对裂缝提取端点,使用Prim算法构造最小生成树实现路面裂缝的连接,同时使用裂缝方向、对比度特征去除连接中的强制连接,可以实现平面图像上具有相同方向、不同长度、不同位置裂缝的连接。

(3)为了去除强制伪连接,在连接的基础上,结合原图,对连接区域,提取局部裂缝,在原检测出来的裂缝上进行填充,可以使连接区域更接近实际裂缝。

(4)实验结果表明,本文算法明显提高了裂缝检测目标的连续性,与人工分割结果非常接近。

[1] 徐志刚.基于多特征融合的路面破损图像自动识别技术研究[D].西安:长安大学,2012.

[2] Huang Y,Xu B.Automatic Inspection of Pavement Cracking Distress[J].Journal of Electronic Imaging, 2006,15(1).

[3] 交通部公路科学研究院上海市公路管理处.JTG H20-2007公路技术状况评定标准[M].北京:人民交通出版社,2008.

[4] Wang K C P.Elements of Automated Survey of Pavements and a 3D Methodology[J].Journal of Modern Transportation,2011,19(1):51-57.

[5] Nejad F M,Zakeri H.An Optimum Feature Extraction Method Based on Wavelet-radon Transform and Dynamic Neural Network for Pavement Distress Classification[J]. Expert Systems with Applications,2011,38(8):9442-9460.

[6] 徐志刚,赵祥模,宋焕生.基于直方图估计和形状分析的沥青路面裂缝识别算法[J].仪器仪表学报,2010, 31(10):2260-2266.

[7] Huang Y,Xu B.Automatic Inspection of Pavement Cracking Distress[J].Journal of Electronic Imaging, 2006,15(1).

[8] Oh H,Garrick N W,Achenie L E K.Segmentation Algorithm Using Iterative Clipping forProcessing Noisy Pavement Images[C]//Proceedings of the 2nd International Conference on Imaging Technologies:Techniques and Applications in Civil Engineering.[S.1.]:IEEE Press. 1998:259-267.

[9] 杨 松,邵龙潭,郭晓霞,等.基于骨架和分形的混泥土裂缝图像识别算法[J].仪器仪表学报,2012, 33(8):1850-1855.

[10] 邹 勤,李清泉,毛庆洲.利用目标点最小生成树的路面裂缝检测[J].武汉大学学报:信息科学版,2011, 36(1):71-75.

[11] Cheng H D,Miyojim M.Automatic Pavement Distress Detection System[J].Information Sciences,1998,108(1): 219-240.

[12] Andaló F A,Miranda P A V,Torres R S,et al.Shape Feature Extraction and Description Based on Tensor Scale[J].Pattern Recognition,2010,43(1):26-36.

[13] Tsai Y C,Kaul V,Mersereau R M.Critical Assessment of Pavement Distress Segmentation Methods[J].Journal of Transportation Engineering,2009,136(1):11-19.

编辑 索书志

Pavement Crack Connection Algorithm Based on Prim Minimum Spanning Tree

REN Liang,XU Zhigang,ZHAO Xiangmo,ZHOU Jingmei
(School of Information Engineering,Chang’an University,Xi’an 710064,China)

When the digital image processing technology is used to detect the cracks on the pavement,it is very hard to detect an intact structure for the cracks because parts of the cracks are very narrow,or shadowed by other objects,or filled with dust.These seriously affects the accuracy of the crack parameter measurement and damage index evaluation.Aiming at the problems above,a pavement crack connection algorithm using Prim minimum spanning tree is proposed.The ridge detection method is used to mark out all the suspicious cracks targets,with the shape features of cracks to remove the noises like spots or blocks.So all the long or obvious cracks are remained.Using the morphology method,the endpoints of the remained crack segments are extracted,and the Prim algorithm is used to construct a minimum spanning tree and makes all the discontinuous cracks connected.All the forced pseudo connections are deleted through the orientation and contrast characteristics of the cracks.On the basis of connection,the cracks are enhanced by filling operation and an intact crack structure is acquired.200 pavement images with cracks are tested,and the Hausdorff distance is used to evaluate the performance of various algorithms.Experimental results show that the proposed algorithm significantly improves the continuity of the detected crack targets,the detection accuracy rate of which is higher than other algorithms with by 6～13 percentage.

traffic engineering;pavement mainteance;crack detection;Prim minimum spanning tree;crack connection; Hausdorff distance

1000-3428(2015)01-0031-06

A

TP751.1

10.3969/j.issn.1000-3428.2015.01.006

国家自然科学基金资助项目(51278058);中央高校基本科研业务费专项基金资助项目(2009JC114,2010ZY007,2010JC056);陕西省自然科学基金资助项目(S2013JC9397)。

任 亮(1989-),男,硕士研究生,主研方向:图像处理;徐志刚(通讯作者),副教授、博士;赵祥模,教授、博士;周经美,博士研究生。

2014-02-18

2014-03-13 E-mail:945357125@qq.com

中文引用格式:任 亮,徐志刚,赵祥模,等.基于Prim最小生成树的路面裂缝连接算法[J].计算机工程,2015,41(1): 31-36.

英文引用格式:Ren Liang,Xu Zhigang,Zhao Xiangmo,et al.Pavement Crack Connection Algorithm Based on Prim Minimum Spanning Tree[J].Computer Engineering,2015,41(1):31-36.