一种改进的实时嵌入式系统容错优化方法

刘浩波,李军义,李仁发

(湖南大学信息科学与工程学院,长沙410082)

一种改进的实时嵌入式系统容错优化方法

刘浩波,李军义,李仁发

(湖南大学信息科学与工程学院,长沙410082)

容错技术中硬件冗余会产生较高的设计和生产成本。针对该问题,提出一种改进的实时嵌入式系统容错优化方法,基于检查点容错技术综合分析系统故障性能、硬实时任务时间约束和软实时任务的效用函数值。以设计的容错模型为基础,计算系统故障概率保证其在故障最大概率值内,给出硬任务截止时间确定可调度性,并应用改进的禁忌搜索算法获得软任务效用函数最佳值,算法有2种简单的邻节点结构,其禁忌准则遵循邻节点方法禁忌,优化效率明显改善。实验结果表明,该方法可进行故障分析等综合分析,并能迅速获得最大效用函数值。

容错优化方法;实时嵌入式;检查点技术;系统故障分析;实时调度算法

1 概述

目前,实时嵌入式系统在经济、科学等多个领域起着重要作用,对及时性及可靠性的要求不同,实时嵌入式系统分为硬实时系统和软实时系统[1]。软实时系统常应用于手机、PDA等方面,在某些情况下能容忍一定量延时,出现故障虽不会导致灾难性后果,但也会明显降低系统服务质量。硬实时系统常应用于航空航天、核工业控制、电力监控及医学应用等要求实现全部功能而且有严格时间约束的领域,若系统出现故障或者不能满足时间约束,后果将不堪设想[2]。因此,提高实时嵌入式系统的容错能力是一项重要的研究工作。容错技术最早由文献[3]提出,是最重要的系统可靠性保障手段[4]。实时嵌入式系统主要通过基于软件冗余的复制、基于时间冗余的重新执行、基于错误回卷恢复的检查点技术以及硬件冗余等技术实现容错。而单独针对硬实时任务或软实时任务的容错研究较为常见,将硬实时和软实时任务整合到相同的平台上进行容错优化一直是近年来研究的热点。

迄今为止,关于这方面的容错优化已有不少文献,V.Izosimov等人提出系统故障概率(SFP)分析方法,结合硬化级别的提高和重新执行技术确保系统架构满足可靠性要求[5-6]。该方法只适应于考虑硬化处理器和重新执行实现容错的情况。之后,文献[7]提出可靠性优化系统故障树(SFT)分析方法,基于组件故障概率结合硬件复制和软件重新执行技术计算系统级概率。该方法适用于硬软冗余实现容错的情况。考虑硬件硬化级别或者硬件复制往往会产生高设计和高生产成本,适用性相对减弱,依靠软件容错技术进行可靠性优化的分析成为一个非常重要的课题。已有不少文献应用软件容错技术综合分析时间和开销约束进行优化设计,实现在限定资源或最大化利用率的情况下满足时间约束的容错方案[8-10]。然而,这类型的容错方案并未结合容错技术进行系统故障优化的分析。故障分析具体指以容错映射方案为基础,分析系统故障概率与系统故障最大概率值的关系。

所谓优化分析,即最优执行方案,具体是指任务映射处理器问题。任务映射处理器问题可描述为,已知m个任务和n个处理器,各任务均需要映射到处理器上,满足各任务符合要求的调度即可终止。它是许多实际调度问题的简化模型,是典型的NP-hard问题。因此,对其进行研究具有重要的理论意义和工程价值。近年来使用优化算法解决这类复杂问题变得越来越流行,在优化算法中,禁忌搜索[11-12]、遗传算法和模拟退火算法[13]等寻优技术是求解非线性优化问题的新方法。其中遗传算法有很高的并行性,但存在早熟和局部收敛等问题;模拟退火算法搜索时间相对较长;禁忌搜索起源于组合优化在非线性覆盖问题中的应用,它能有效利用全局信息和搜索中获得的信息,可克服遗传算法的局部性,又比模拟退火算法的搜索速度更快[14]。文献[15]提出应用禁忌搜索算法启发式解决任务映射处理机问题获得满足优化条件的最佳方案。然而,其禁忌列表限于禁忌当前解决方案,禁忌空间较小,使得优化算法在避免局部优解时性能存在一定局限性。

文献[16]研究了如何在实时嵌入式系统中处理永久性故障问题。系统故障可分为瞬时性故障、周期性故障及永久性故障。由于更大复杂性和更高频率等原因,瞬时故障数量越来越大且更常见,研究如何处理瞬时故障问题成为工作重点。

本文在优化设计方面除了考虑时间和效用约束外,还要考虑系统故障分析研究,提出一种改进的优化分析方法。该分析方法的容错策略设计如下:硬实时任务使用最早截止时间先执行,由于检查点技术比复制方法资源利用率更高,比重新执行更能节省容错所需的重执行时间,可相应提高效率,因而采用检查点回卷恢复技术实现容错。软实时任务使用最短执行时间后执行,不建立检查点,遇故障直接丢弃。考虑软实时任务高度可变的执行时间,提出了自定义效用函数表示软任务执行利用率,利用率与软任务是否在截止时间内完成无关。在任务映射处理器问题上,提出一种改进的禁忌搜索算法,设计了2种简单的邻节点结构,在判断禁忌时,将交换方法获得的候选方案禁忌,致使禁忌列表内包含多种解决方案,可获得最佳解决方案。

2 问题公式化

2.1 容错模型

本文以处理瞬时故障和硬软混合实时任务为重点,以容错方案满足可靠、可调度和效用函数最佳为目标,考虑一个典型的由多处理器和混合硬软实时容错任务集构成的分布式系统,由以下定义进行形式化描述:

定义1分布式架构由内存子系统、通信控制器和中央处理单元组成,可描述为一组处理器集合。

定义2针对混合硬软实时容错应用映射到分布式系统架构中,将一组实时任务集A分为硬实时任务和软实时任务。A→{Hard,Soft}分别确定任务是硬实时或者软实时。

为方便进行形式化描述,硬实时任务标记如下:

软实时任务标记如下:

软实时任务的效用函数是软任务完成时间的非递增单调函数,3个效用函数定义如下:

2.2 系统容错分析

系统容错分析包括3个阶段:故障分析,可调度性分析和软任务效用函数值最佳分析。在故障分析阶段,以容错模型为基础,分析系统故障概率与故障最大概率的关系。计算系统故障概率的过程中,只需要求出在相应处理器上的任务当时遇故障概率。

输入条件中已知各任务在各处理器上的执行遇故障概率,i和j分别表示任务号和处理器号,N表示处理器,硬实时用h表示,插入f个检查点;软实时用s表示,不需插入检查点,遇故障丢弃。在运行过程中,可分4种情况:软实时不遇故障、硬实时不遇故障;软实时不遇故障、硬实时遇故障;软实时遇故障、硬实时不遇故障;软实时遇故障、硬实时遇故障。

(1)处理器j相应概率pr(0,h,f;0,s;Nj)和处理器相应概率pr(0,h,f;0,s;N):

在此种情况下,每个任务成功执行。g表示硬实时任务被插入检查点的第g节。即使被插入检查点,任务还是执行在同一处理器上。M(P)=N函数表示任务P映射在处理器N上。

(2)处理器j相应概率pr(kb,h,f;0,s;Nj)和处理器相应概率pr(kB,h,f;0,s;N)。

基于f次插入检查点、kb次遇故障分析处理器上任务的故障概率。假设每任务插入检查点个数相同。

m大于等于0,如果m＞0,表示遇故障重新执行。G表示所有插入检查点组合集,gx∈G表示遇故障段集,g表示检查段,所有硬任务执行段遇故障总数不得超过kB。举例说明如图1所示。

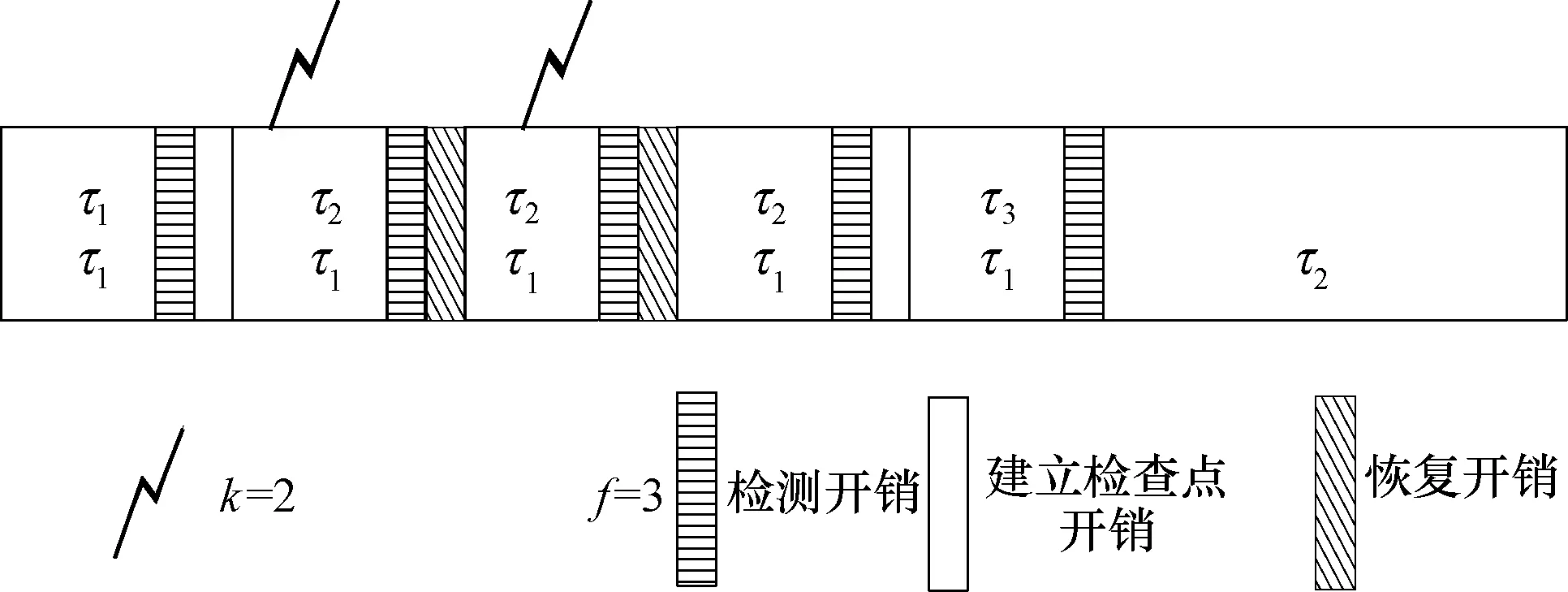
图1 软实时不遇故障、硬实时遇故障实例图

假设任务集A由硬实时任务τ1和软实时任务τ2组成,k=2个瞬时错误可能发生,f=3次插入检查点。硬实时任务各任务段执行后进行错误检测,发现成功执行,可建立检查点;遇故障两次,产生恢复开销,后成功执行方建立检查点;成功运行紧接着,执行τ2,无故障,且不建立任何检查点。

(3)处理器j相应概率pr(0,h,f;kc,s;Nj)和处理器相应概率pr(0,h,f;kC,s;N):

s∈S表示软任务无遇故障,s∉S表示软任务遇故障。各软任务遇故障数目控制在kc,总数控制在kC。

(4)处理器j相应概率pr(kd1,h,f;kd2,s;Nj)和处理器相应概率pr(kD1,h,f;kD2,s;N):

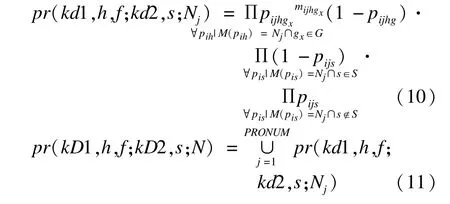
所有硬任务执行段遇故障总数不得超过kD1。s∈S表示软任务无遇故障,s∉S表示软任务遇故障,且遇故障总数控制在kD2。gx∈G表示遇故障段集,g表示检查段。

系统保证故障分析要求应满足pr≤γ,γ为系统故障的最大概率。

在可调度性分析阶段,确保硬实时任务完成时间hct满足,hct＜截止时间D,则可调度。并在这基础上,计算软任务的效用函数值。软任务效用函数值最佳分析使用2.3节的禁忌搜索算法启发式优化实现。

2.3 改进的禁忌搜索算法

禁忌搜索算法是在邻域搜索候选方案的基础上,通过引入一个灵活的存储结构和相应的禁忌准则来避免迂回搜索,同时通过特赦准则赦免一些优良的解决方案,进而保证多样化的有效搜索以最终实现全局的优化。引言中已提到任务映射处理器问题是许多实际调度问题的简化模型,是典型的NP-hard问题,并且使用优化算法解决这类复杂问题变得越来越流行,而优化算法中,禁忌搜索可克服遗传算法的局部性,又比模拟退火算法的搜索速度更快。已有文献提出应用禁忌搜索算法解决任务映射处理器问题,基于此,提出一种改进的禁忌搜索算法,设计了2种简单的邻节点结构,在判断禁忌时,将交换方法获得的候选方案禁忌,通过此算法确定任务映射方案,以期获得容错可调度方案中软任务效用函数值最佳的优化方案。禁忌搜索算法中输入值为应用集A和处理器集N,映射M解决方案作为输出。

禁忌搜索算法的关键参数和操作设计如下:

(1)初始方案产生

禁忌搜索方法对初始方案的依赖性较强,好的初始方案能使禁忌搜索尽快收敛到更好的解决方案,而较差的初始方案则会降低禁忌搜索的收敛速度,很难或不能获到最优解决方案。有些算法选择初始解决方案的时候并不考虑是否可行,本文采用贪心算法以获得满足可靠性和可调度要求的初始方案,以此缓解对初始方案的依赖。

(2)邻域产生函数

邻域产生函数主要使用移动来实现。

1)交换

如图2所示,在此初始方案中,圆形表示为软实时任务,正方形表示硬实时任务,随机从一个处理器中随机选择一个任务,随机与另一个处理器中一个任务作交换。如图3所示,选择任务1与任务2作交换。

图2 初始方案实例

图3 交换方案实例

2)重新映射

随机从一个处理器中随机选择一个任务,作重新映射。如图4所示,选择任务1重新映射,映射到另一个处理器中。

图4 重新映射方案实例

出于改善算法的优化时间性能的考虑,通过邻域结构可以产生大量的邻域方案,而候选方案仅取其中的少量最佳状态。

(3)禁忌准则

该禁忌列表存储着通过交换方法获得的候选解决方案。之所以选择禁忌交换这一邻域产生函数,是考虑到交换方法需要牵涉到2个不同处理器,而重新映射首次实现的概率明显优于交换实现。以任务映射处理器问题为例,某候选方案是通过交换产生的邻节点,如图3实际是由处理器1的任务1和处理器2的任务2作交换获得,但交换可获得更多候选方案,通过交换获得的邻节点均被禁忌。相比单一的禁忌某解决方案,该禁忌准则的设计可有助于快速逃离局部最优解决方案。

(4)特赦准则

禁忌准则可能限制了某些更优解决方案,所以需用特赦准则,以释放虽被禁忌却很优的解决方案。本文设计的特赦准则是,若一定数量的解决方案均被禁忌,则设置这些方案中目标值最大的为当前最好的解决方案。

(5)终止准则

为了使算法具有优良的优化性能或时间性能,必须设置一个合理的终止准则来结束整个搜索过程。经过实验,算法运行可以采用是否找到最佳解和总的循环次数两种终止原则,从效果上看都还不错。由于VC++循环的效率较高,运行的时间相对不是很长,所以采用总的循环次数限制作为终止原则,如若在循环次数前可获得最佳方案则也终止。

3 容错优化设计

硬实时任务应用检查点技术实现瞬时故障容错,软实时任务遇故障直接丢弃。基于此,对系统实现故障分析、对硬实时任务实现可调度性分析和对软实时任务实现效用函数值最大化分析。一般来说,实现设计时必须着重两个部分,即映射和调度。映射时使用改进的禁忌搜索算法优化处理器上应用,调度混合硬软任务时,分别用最早截止时间和最短执行时间调度硬实时和软实时任务。

实现过程选出满足故障分析要求和可调度性要求的映射方案,否则及早扩展分析,即优化迭代映射和策略分配,以获得最优组合。

4 算法实现

算法实现过程如下:

(1)算法设计思路

根据数据项建立2个类,先使用一种贪心算法获得一个初始可行的解决方案,再应用改进的禁忌搜索算法反复迭代寻优,获得通过容错优化分析要求的目标函数值最优的解决方案。算法流程如图5所示。

图5 本文算法流程

(2)贪心算法设计思路

获得初始方案后,判断方案是否满足故障分析要求和可调度性,如若两者存一不能通过,则返回改变方案,重新调度判断,直到初始方案满足故障分析要求和可调度性。

(3)禁忌搜索算法设计思路

步骤1获得初始化方案后,设置当前初始方案为目前最佳方案。

步骤2在当前方案的n1个邻节点中选择满足故障分析和可调度性要求的n2个方案,在n2个方案中选择n3个最好的候选方案,对n3个候选方案进行检测,如若属于通过交换方法获得的方案,则将其禁忌。再在这n3个候选方案中选择最好的未禁忌解决方案,指定为当前方案。如果所有n3方案都被禁忌了,那么选择最佳禁忌方案为当前方案,注意更新禁忌表。

步骤3如果当前方案比目前最好的方案要好,则目前最好的方案设置为当前方案。判断是否更新了M次迭代,如若是,则终止。并判断是否获得了最佳方案,如若是,则终止。否则,跳回步骤2。

5 实验结果与分析

该分析和优化算法用 VC++实现,运行在4 GHz CPU和4 GB内存的Windows系统中,每个任务遇故障概率在1·10-6和1·10-5之间随机产生,设置每个硬实时任务遇故障数在0～2之间随机产生,每个软实时任务遇故障数在0～1之间随机产生,每个硬实时任务被插入3个检查点。

第1部分实验是关于系统故障分析的实验,对于故障分析的度量,可达到的系统故障最大概率越小,故障分析性能越好。因已有文献中针对重新执行进行系统故障分析,本文采用检查点回卷恢复的系统故障分析分别与无容错分析、重新执行的系统故障分析作比。本文用到的检查点回卷分析法其故障最大概率可达到1·10-16。在嵌入式系统设计中,一个重要的步骤就是确定满足故障分析要求的任务分配情况。处理器数量满足2～5的任意平台下,设计硬实时任务数量分别为2～6,每次运行方案里都保证软实时任务数量为3。

关于运行次数的分析如表1所示。以硬实时任务数为2、软实时任务数为3、处理器数为2的情况为例。

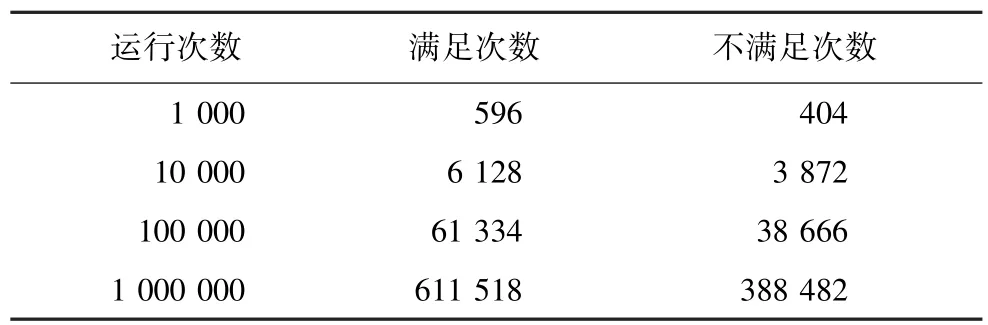
表1 运行次数分析

从表1可看出,对比实验取运行次数100 000次,可达高度稳健。如表2所示,运行次数100 000次时检查点回卷恢复的故障分析统计情况。

表2 检查点技术的故障分析统计

表2是处理器数为3时的遇故障通过次数及概率统计表。从表中可以看出,任务分配如硬实时任务为4,软实时任务为3时,已经可以达到很高的可靠性值。即能保证90%满足故障分析目标,并因此确定任务分配情况。

如上所述,分别对其余2种情况进行分析,得出检查点回卷恢复的故障分析与无容错故障分析、重新执行的故障分析对比如图6所示。

图6 故障分析对比

重新执行故障分析和无容错故障分析可达到的故障最大概率分别为1·10-15和0.999 99,均比检查点回卷故障分析达到的故障最大概率要大。承上所述,度量故障性能的标准是,可达到的故障最大概率值越小,故障性能越显著。由此看来,检查点回卷故障性能明显优于其余两者。如图6所示的对比实验,其x轴表示任务分配情况,分别是硬任务数为2～6和软任务数为3,y轴表示通过概率,即达到故障最大概率值的概率,可知检查点回卷故障分析达到故障最大概率值的稳定性能亦优于其余两者。

第2部分实验是关于可调度性的实验,对于可调度性分析的度量,专门针对硬实时任务的完成时间和截止时间,完成时间小于截止时间记为可实现调度。达到的可调度概率值越大,可调度性越好。对于嵌入式实时系统中常见的瞬时故障,目前重点研究的容错处理方法是基于任务重新执行的容错调度方法和基于检查点技术的卷回恢复方法,重新执行是通过时间冗余实现容错,而检查点技术是通过错误回卷恢复实现容错,本文采用后者,现对这2种方法作对比实验,各运行100 000次,任务执行时间在100～1 000之间随机产生,硬实时任务截止时间在1 000～1 800之间随机产生,建立检查点开销、检测开销和恢复开销均设计为2,以上参数经过多次试验验证。基于第1部分实验,设计硬实时任务数为4,软实时任务数为3,本文采用检查点技术的可调度性统计情况见表3。

如表3所示,随着处理器规模的扩大,处理器上任务调度负载相应减少,可调度性越高。考虑到处理器数目的增多,系统开销相应增加,所以,处理器数目也会有一定限制。承上所述,分别对上述两种情况进行可调度性分析,得出检查点技术可调度性与重新执行可调度性的对比如图7所示。

表3 检查点技术的可调度性统计

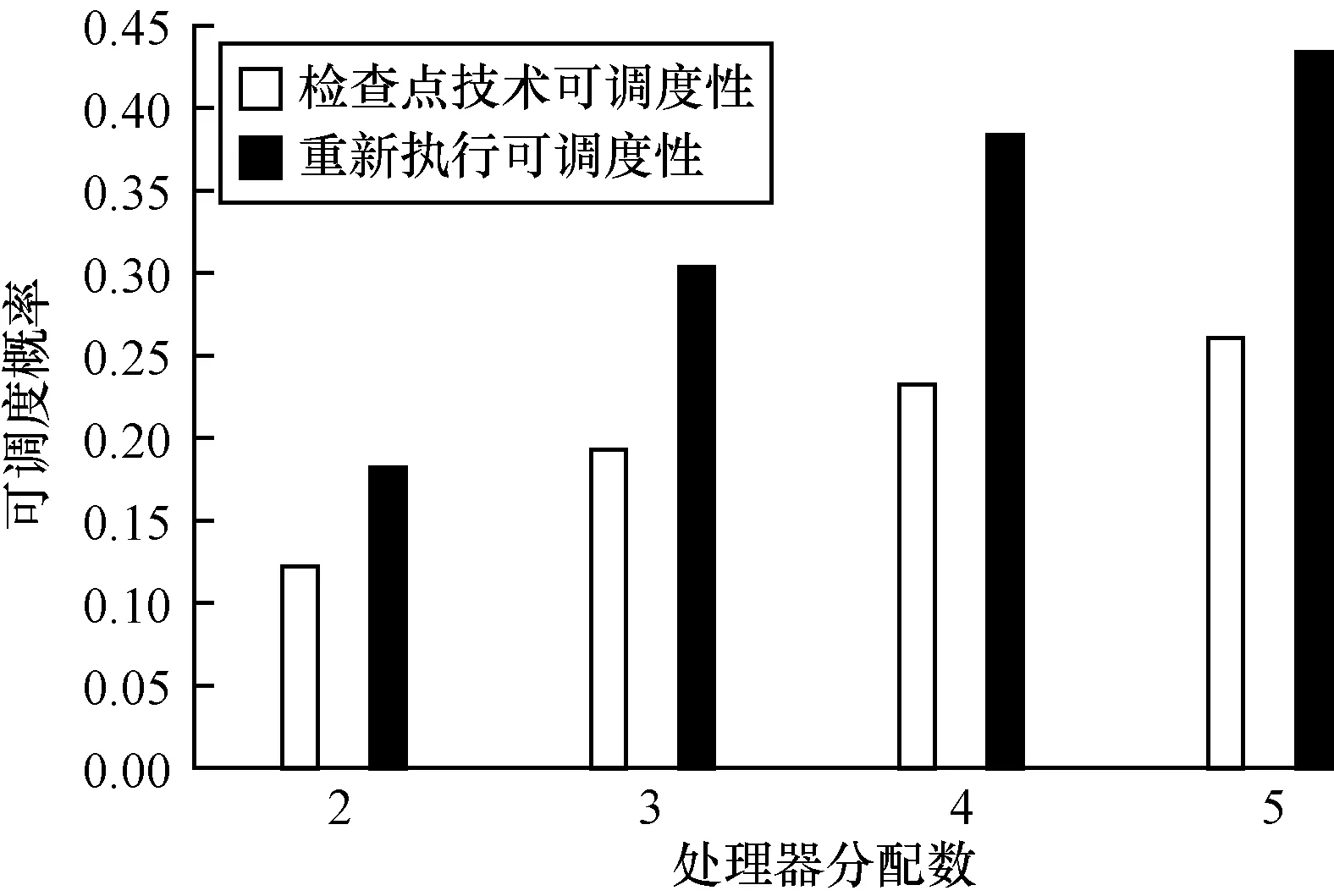
图7 可调度性分析对比

从图7中可以看出,检查点技术明显优于重新执行的可调度性能。相比重新执行,检查点技术能够缓解时间冗余的部分压力。

第3部分实验是关于禁忌优化的实验,对于禁忌优化的度量,主要考虑参数为软实时任务取得的效用函数值、计算时间和迭代次数,效用函数值越大,计算时间越短,迭代次数越少,表明优化效果越明显。已有文献中设计禁忌当前解决方案,本文采用改进的禁忌搜索算法与已有文献中的算法做优化对比。基于第1和第2部分实验,设计硬实时任务数为4,软实时任务数为3,处理器数为5。由上述实验可知,选择这些参数是最有效的值。用改进的禁忌搜索算法对其求解时还采用了以下参数,分别运行100次,各求平均值,每次运行迭代300次。若提前达到效用函数最佳值,则终止迭代。数值比较结果如表4所示。

表4 函数值比较结果

通过以上实验计算,可以总结改进的禁忌搜索算法的以下特点:

(1)算法求得的最终解其质量较高;

(2)算法的收敛速度较快,计算效率较高;

(3)算法的稳健性较强。

curSolution-tabu方案中禁忌列表只禁忌某个解决方案,不如设计禁忌交换这一邻域产生函数更客观,禁忌列表内包括搜索邻节点方法而获得的所有解决方案,扩大了禁忌范围。相比已有文献中单一的禁忌某解决方案,该禁忌准则的设计可有助于快速逃离局部最优解决方案,从而可更快速有效地获得最佳解决方案。

6 结束语

本文提出一种改进的实时嵌入式系统的容错优化方法,该优化方法基于检查点容错技术综合分析系统故障性能、硬实时任务时间约束和软实时任务的效用函数值。以设计的容错模型为基础,改进的优化方法计算了系统故障概率,保证其在故障最大概率值内,给出硬任务截止时间确定可调度性。此外,改进了禁忌搜索算法,提高了收敛和计算速度,反复迭代寻优以获得满足容错优化的最佳方案。

根据上述总结,本文下一步工作主要包括以下3个方面:(1)任务遇故障后重新调度,可提高或降低其优先级,而不是继承其正常运行时优先级; (2)关于检查点的研究,可以考虑不同等间隔插入检查点;(3)禁忌搜索算法改进问题。首先可以考虑获得邻节点的方法,可以取交叉。交叉操作是基于任务集交叉,即先把任务分成2个非空集合,集合A或者集合B,把处理器分成2个非空集合,集合C或者集合D,从A集合中分别随机选择属于集合A的任务随机映射到处理器集C中的处理器,从集合B中分别随机选择属于集合B的任务随机映射到处理器集D中的处理器。其次可以考虑禁忌列表的改善,设计禁忌区间,若候选方案的适配值在禁忌区间内,则将其方案禁忌。

[1] Kopetz H.Real-time Systems-design Principles for Distributed Embedded Applications[M].[S.1.]: Kluwer Academic Publishers,1997.

[2] Li Qing.Real-time Concept for Embedded Systems[M].[S.1.]:CMP Books Inc.,2003.

[3] 袁由光,陈以农.容错与避错技术及其应用[M].北京:科学出版社,1992.

[4] 陈 宇,熊光泽,杨 春.支持自适应容错的多处理器实时操作系统[J].计算机科学,2002,29(3):125-128.

[5] Izosimov V,Polian I,Pop P,et al.An aLysis and Optimization of Fault-tolerant Embedded Systems with Hardened Processors[C]//Proceedings of Conference on Design,Automation&Test in Europe.Nice,England: [s.n.],2009:682-687

[6] Izosimov V.Scheduling and Optimization ofFaulttolerant Distributed Embedded Systems[D].Sweden, Linkoping:Linkoping University,2009.

[7] Huang Jia,Blech J O,Raabe A,et al.Reliability-aware Design Optimization forMulti-processorEmbedded Systems[C]//Proceedings of Conference on Digital System Design in Europe.Oulu,Finland:[s.n.],2011: 239-246.

[8] Izosimov V,Pop P,Eles P,et al.Design Optimization of Time-and Cost-constrained Fault-tolerantDistributed Embedded Systems[C]//Proceedings of Conference on Design,Automation and Testin Europe.Munich, Germany:[s.n.],2005:864-869.

[9] Pop P,Izosimov V,Eles P,et al.Design Optimization of Timeand Cost-constrained Fault-tolerantEmbedded systems with checkpointing and Replication[J].IEEE Transactions on Very Large Scale Integration Systems, 2009,17(3):389-402.

[10] Izosimov V,Eles P,Peng Z.Value-based Scheduling of Distributed Fault-tolerant Real-time Systems with Soft and Hard Timing Constraints[C]//Proceedings of IEEE Workshop on Embedded Systems for Real-time Multimedia.Scottsdale,America:[s.n.],2010:31-40.

[11] Glover F.Tabu Search-part I[J].ORSA Journal on Computing,1989,1(3):190-206.

[12] Glover F,Tabu Search-part II[J].ORSA Journal on Computing,1990,2(1):4-32.

[13] Davis L.Genetic Algorithmsand Simulated Annealing[M].London,England:Pitman Publishing,1987.

[14] 张文化,刘素华,候惠芳.一种用于特征选择的禁忌搜索算法[J].计算机应用与软件,2010,27(5):125-128.

[15] Saraswat P K,PopP,MadsenJ.TaskMappingand Bandwidth Reservation for Mixed Hard/soft Fault-tolerant Embedded Systems[C]//Proceedings of the 16th IEEE Symposium on Real-time and Embedded Technology and Applications.Stockholm,Sweden:[s.n.],2010:89-98.

[16] Saraswat P K,Pop P,Madsen J.Task Migration for Faulttolerance in Mixed-criticality Embedded Systems[C]// Proceedings of the 2nd Workshop on Adaptive and Reconfig-urable Embedded Systems.Grenoble,France: [s.n.],2009:125-131.

编辑 索书志

An Improved Fault Tolerance Optimization Method of Real-time Embedded System

LIU Haobo,LI Junyi,LI Renfa
(College of Information Science and Engineering,Hunan University,Changsha 410082,China)

For the hardware redundancy fault tolerance technology tends to produce the defect of high design and high production costs,this paper puts forward an improved fault tolerance optimization method of real-time embedded system. The optimization method is based on checkpoint fault tolerance technology,and it comprehensively analyzes system failure performance,hard real-time task time constraints,and the utility function value of the soft real-time tasks.It is based on the design of fault tolerance model,the improved optimization method calculates the system failure probability, determines the schedulability of hard tasks,and uses an improved tabu search heuristic optimization to obtain utility function best value of soft tasks.The tabu search algorithm has two neighboring nodes of simple structure,it is tabu guidelines follow the tabu of adjacent node method and optimization efficiency is improved significantly.Experimental results show that the fault tolerance optimization method can carry on fault analysis and so on,and can quickly obtain maximum utility function.

fault tolerance optimization method;real-time embedded;checkpoint technology;system fault analysis; real-time scheduling algorithm

1000-3428(2015)01-0012-07

A

TP302

10.3969/j.issn.1000-3428.2015.01.003

国家“863”计划基金资助项目(2012AA01A301-01);广东省产学研基金资助重大项目(2011A091000027);广东省产学研基金资助重大项目“基于北斗/GPS的智能车载信息终端关键技术研究与产业化”([2012]391)。

刘浩波(1989-),女,硕士研究生,主研方向:嵌入式容错,软件测试;李军义,副教授、博士;李仁发,教授、博士。

2014-02-12

2014-04-05 E-mail:15974144754@163.com

中文引用格式:刘浩波,李军义,李仁发.一种改进的实时嵌入式系统容错优化方法[J].计算机工程,2015,41(1): 12-18.

英文引用格式:Liu Haobo,Li Junyi,Li Renfa.An Improved Fault Tolerance Optimization Method of Real-time Embedded System[J].Computer Engineering,2015,41(1):12-18.