基于改进SIFT的SAR图像配准方法

张雄美,易昭湘,蔡幸福,宋建社

(第二炮兵工程大学,西安710025)

基于改进SIFT的SAR图像配准方法

张雄美,易昭湘,蔡幸福,宋建社

(第二炮兵工程大学,西安710025)

针对尺度不变特征变换(SIFT)配准方法在处理SAR图像时精度不高的问题,提出一种基于改进SIFT的精确配准方法。在提取关键点SIFT描述子及其邻域多尺度自卷积矩不变特征的基础上,利用基于典型相关分析的融合算法对SIFT与矩不变特征进行融合,形成新的关键点描述子,使用阈值实现粗匹配,并结合关键点的距离与邻域灰度相关性构建相似矩阵,采用奇异值分解方法精确确定匹配点对,求出仿射变换模型参数,从而完成图像配准。实验结果表明,该方法的配准结果优于SIFT方法,且配准精度达到亚像素级。

SAR图像配准;尺度不变特征变换;多尺度自卷积;典型相关分析;奇异值分解

1 概述

图像配准是将不同时间、不同视角或不同传感器获取的关于同一场景的2幅或多幅图像进行对准并确定彼此对应关系的过程[1]。图像配准是图像融合、变化检测、多通道图像恢复等的前提与基础[2-3]。配准的精度直接影响其后续图像处理工作的结果。

目前,常用的图像配准方法有基于区域相关的配准方法和基于特征的配准方法[4]。其中,前者基于图像的灰度信息进行配准,易受相干斑噪声、辐射差异等因素的影响,配准精度不高,效果不是很理想,基于特征的配准方法则是基于提取的显著性特征进行配准,对噪声、辐射差异等具有较强的鲁棒性,获得的结果更加稳定、准确,是图像配准领域的研究热点。

在众多基于特征的配准算法中,尺度不变特征变换(Scale Invariant Feature Transform,SIFT)算法[5]由于具有较好的尺度、旋转不变性,对光照、噪声和仿射变化具有较强的鲁棒性,且提取的关键点稳定、数量丰富等优点而得到了广泛的应用。但是,该算法不具备仿射不变性,在处理几何变化较大的2幅图像时存在性能退化的现象;此外,该算法的相似性度量只考虑了描述子间的距离,而没有考虑关键点的位置及其邻域的灰度相关性,在处理灰度弱相关图像时存在较大的误差[6-8]。

基于上述分析,在引入多尺度自卷积(Multi-Scale Autoconvolution,MSA)矩不变量与基于典型相关分析(Canonical Correlation Analysis,CCA)的特征融合算法的基础上,本文提出一种基于SIFT与MSA的SAR图像配准方法,结合关键点邻域的仿射不变特征,且配准过程中充分利用关键点的位置及其邻域的灰度相关性。

2 SIFT算法

SIFT算法是在总结现有的特征检测方法的基础上提出的一种基于多尺度空间理论的、对图像旋转和缩放保持不变性的特征匹配算法[5]。SIFT算法分为关键点检测和描述子生成与匹配2个部分:

(1)关键点检测及定位

首先采用唯一线性的高斯卷积核与原图像I(x,y)进行卷积,得到高斯差分(Difference of Gaussian, DoG)图像,通过比较DoG图像中各采样点的幅值确定极值点的位置、尺度,然后去除低对比度的极值点和不稳定的边缘响应点得到最终的关键点集。其中,DoG图像定义为:

其中,(x,y)为空间坐标;σ为尺度因子;k为常数乘积因子。

(2)SIFT描述子生成与匹配

首先计算关键点邻域像素的梯度方向,并绘制梯度直方图,直方图峰值对应的方向即为关键点的主方向,并将坐标轴旋转到关键点主方向,以保证旋转不变性。然后,以关键点为中心、梯度方向为主方向取大小为16×16的邻域,并将其分成16个4×4大小的子块,每一子块计算8个方向的梯度方向向量,这样就可得到16×8共128维SIFT描述子。

在关键点匹配阶段,若图像中的某个SIFT特征与另一幅图像的最近邻特征和次近邻特征间的距离比小于预先设定的阈值,则认为这2个最近邻特征匹配。

3 MSA特征

MSA方法是Rahtu在引入概率模型的基础上提出的一种基于点的图像不变特征提取方法,不仅具有尺度不变性、旋转不变性、仿射不变性等优良特性,还具有较好的抗噪性[9-10]。

MSA的基本原理为:图像中任意不共线3点的坐标可以线性表示出其他任意一点的坐标,经仿射变换后,这4个点的线性表示形式保持不变。Rahtu正是利用了这种系数不变性构造出了仿射不变量。

设2维仿射变换A=A{T,t},A是一个二阶可逆矩阵。仿射变换A有6个自由度,3个不共线的点对应一个仿射变换。则变量x的仿射变换为:

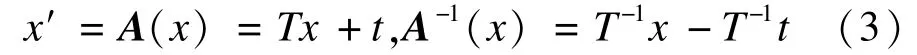
设f(x):R2→R为图像强度函数,其经仿射变换后为:

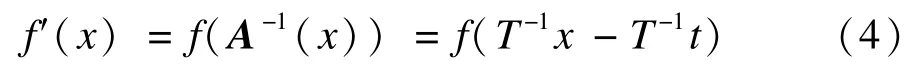
设x0,x1,x2∈R2(x0,x1,x2是服从独立同分布的随机变量)为f(x)定义域中任意的3个点,则以这3个点定义的新的随机变量可表示为:

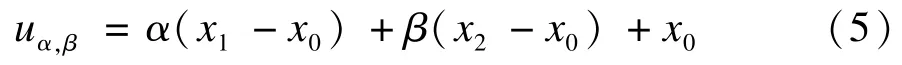
其中,(α,β)是在以x0为原点、x1-x0与x2-x0为单位向量的仿射空间A2中的坐标。若设x′0,x′1,x′2分别为点x0,x1,x2的仿射变换,则有

由上式可知,uα,β经坐标系仿射变换后得到的随机变量u′α,β的坐标仍然是(α,β)。而u′α,β的图像强度函数为:

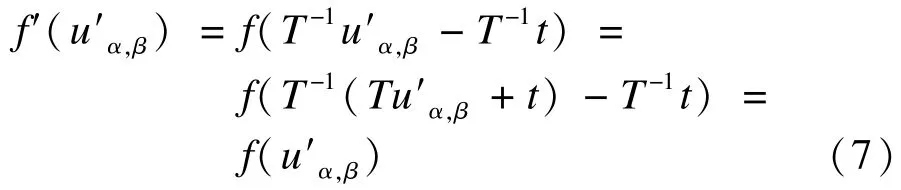
由上式可知,随机变量f(uα,β)与f′(u′α,β)有着相同的分布,因此,其数学期望或任何阶矩也是相等的,这种关系不随仿射变换而变化,因此,是仿射不变的。MSA不变特征即为f(Uα,β)的期望值:

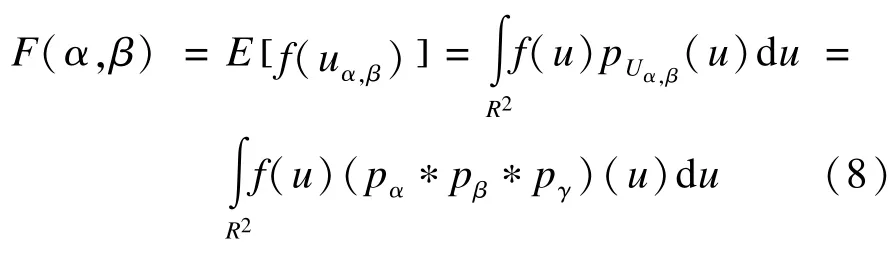
其中,pUα,β(u)=(pα∗pβ∗pγ)(u)为概率密度函数。为了简化运算,利用傅里叶变换将上式转换到频域中进行计算,即:

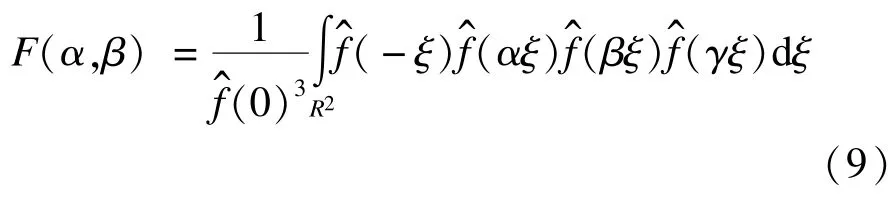
其中,为f的傅里叶变换。

4 改进的SIFT算法

在引入 MSA的基础上,提出了一种改进的SIFT方法。新方法在提取关键点SIFT描述子与关键点邻域MSA矩不变特征的基础上,利用CCA特征融合算法对SIFT与MSA特征进行融合,形成新的关键点描述子,并利用该描述子对提取的关键点进行粗匹配,然后由粗匹配点对的距离及其邻域的灰度相关性构建相似矩阵,最后采用奇异值分解(Singular Value Decomposition,SVD)方法精确确定匹配点对,求出仿射变换模型参数,完成图像配准。具体步骤如下:

步骤1SIFT关键点检测及描述子生成。利用SIFT算法进行关键点检测并生成描述子。设ρ(x,y,σ,θ)为SIFT算法检测到的关键点,其中,(x,y)为点ρ在原图像上的位置,σ,θ分别为点ρ所在的尺度及其主方向。对于每一关键点,计算出128维的SIFT描述子z=(z1,z2,…,z128)。

步骤2MSA关键点描述。利用SIFT算法检测到关键点ρ(x,y,σ,θ)后,首先根据σ值的大小,在点ρ所在的相应尺度上,将坐标轴旋转至关键点的主方向,以确保描述子的旋转不变性,然后以关键点为中心取16×16大小的窗口邻域作为待描述区域。对于每一关键点的待描述区域分别计算不同(α,β)对应的MSA特征,形成该关键点的n维MSA描述子向量f=(f1,f2,…,fn),其中,n为不同(α,β)的点对数。

步骤3基于CCA的SIFT与MSA特征融合。提取关键点的SIFT特征与MSA特征后,利用基于 CCA的特征融合算法[11]融合 SIFT与MSA特征,以形成对关键点更全面、准确的描述子,从而最终提高图像配准的精度及配准算法的稳健性。

步骤4关键点匹配。关键点对间的匹配精度对配准结果有着直接的影响,关键点对间的错误匹配会直接导致整个配准过程的失败。为此,采用SVD匹配算法[12]进行关键点对间的精确匹配。为降低计算复杂度,在进行SVD匹配前先对关键点进行粗匹配,具体方法是:对于提取的2个关键点集,计算2个点集中对应描述子的最近与次近欧氏距离比,当该比值小于预先设定的阈值时,初步确定为匹配点对。

步骤5变换参数估计。得到2幅图像间的N对控制点后,根据仿射变换模型[13]求出变换参数,完成图像配准。

5 实验结果及分析

为验证方法的有效性,利用本文方法分别对有尺度与灰度变化(图像配准实验1)、几何变化(图像配准实验2)的 SAR图像进行配准,并与SIFT算法的配准结果进行了比较。本文算法在提取MSA特征时共采用了29对(α,β)值,即在集合{-1,-0.75,-0.5,-0.25,0.25,0.5, 0.75,1}中任取2个元素组成29对(α,β)值,同时计算前3阶矩,这样每个关键点的MSA特征都是一个29×3=87维的向量;在SIFT与MSA特征融合中,组合特征维数设置为75维;在关键点粗匹配中,由于匹配点对数随着阈值的减小而减少,而匹配点对太少会导致最终的配准精度不高,匹配点对太多又会导致计算量过大,因此粗匹配中的阈值设为0.8。

为了对各方法的配准结果进行定量的比较,采用2幅图像关键点对应坐标的均方根误差(Root Mean Squared Error,RMSE)和匹配正确率(CMR)作为量化指标。

实验1为验证本文方法对2幅尺度与灰度有较大差异的图像配准的有效性,采用武汉地区SAR图像数据进行实验,如图1所示,其中,图1(a)、图1(b)分别为参考图像和待配准图像,图像大小分别为297×277像素、369×465像素。图1(c)给出了本文方法的配准结果。可以看出,2幅图像间存在较大的尺度与灰度差异。

图1 实验1配准结果

实验2为验证本文方法对存在较大几何变化的图像配准的有效性,以图2(a)为参考图像(大小为440×263像素),以对其进行仿射变换后得到的部分图像作为待配准图像(如图2(b)所示,图像大小为200×152像素)进行实验。图2(c)给出了本文方法的配准结果。

图2 实验2配准结果

2种实验下不同方法的配准精度如表1所示。

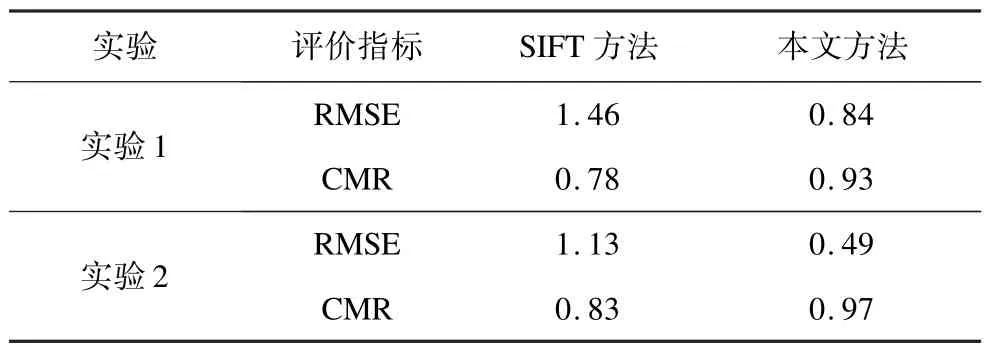
表1 2种实验下不同方法的配准精度

表1实验1给出了本文方法与SIFT方法对图1(a)与图1(b)的配准精度。从表1可以看出,在参考图像与待配准图像间存在较大的尺度与灰度差异时,本文方法的配准精度更高,CMR为0.93, RMSE为0.84。

表1实验2给出了 SIFT方法和本文方法对图2(a)与图2(b)的配准精度。可以看出,相对于SIFT,本文方法的CMR值更高,RMSE值更低,表明本文方法的配准精度更高,且达到亚像素级。同时,相对于实验1,实验2的RMSE值要略低一些,这是由于实验2中的参考图像与待配准图像间只涉及几何变化,避免了灰度变化对配准结果的不利影响。

6 结束语

在引入MSA矩不变特征提取方法的基础上,本文提出一种基于改进SIFT的SAR图像配准方法。在关键点检测阶段,充分利用了SIFT算法在关键点检测上的优势,提取的关键点稳定且数量丰富;在描述子构造阶段,考虑到MSA特征具有尺度不变性、旋转不变性、仿射不变性以及较好的抗噪性等优良特性,通过提取关键点邻域MSA特征对SIFT描述子进行补充,有效降低了描述子对噪声与灰度变化的敏感性;在关键点匹配阶段,在粗配准的基础上结合关键点的位置及其邻域的灰度相关性进行精确匹配,提高了匹配算法对大几何变化与灰度变化的稳健性。实验结果表明,与SIFT方法相比,该方法能有效地处理几何与灰度差异较大的2幅图像间的配准问题,获得了更高的配准精度。由于需要提取关键点的MSA特征并进行融合,本文方法的运行效率低于SIFT算法,如何在保持高配准精度的前提下提高运行效率是下一步的研究方向。

[1] Zitova B,Flusser J.Image Registration Methods:A Survey[J].Imageand Vision Computing,2003, 21(11):977-1000.

[2] Singh A.Digital Change Detection Technique Using Remotely-sensed Data[J].InternationalJournalof Remote Sensing,1989,10(6):989-1003.

[3] White R G.Change Detection in SAR Imagery[J]. International Journal of Remote Sensing,1991,12(2): 339-360

[4] Salvi J,Matabosch C,Fofi D,et al.A Review of Recent RangeImageRegistration Methodswith Accuracy Evaluation[J].Image and Vision Computing,2007, 25(5):578-596.

[5] Lowe D G.DistinctiveImageFeaturesfrom ScaleinvariantKeypoints[J].International Journal of Computer Vision,2004,60(2):91-110.

[6] 赵 明,林长青.基于改进SIFT特征的红外与可见光图像配准方法[J].光电工程,2011,38(9):130-136.

[7] Paganelli C,Peroni M,Riboldi M,et al.Scale Invariant Feature Transform in Adaptive Radiation Therapy:A Tool for Deformable Image Registration Assessment and Re-planning Indication[J].Physics in Medicine and Biology,2013,58(2):287-299.

[8] 王 鹏,王 平,沈振康,等.一种基于SIFT的仿射不变特征提取新方法[J].信号处理,2011,27(1):88-93.

[9] Rahtu E,Salo M,Heikkila J.Affine Invariant Pattern Recognition Using Multi-scale Autoconvolution[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(6):908-917.

[10] Rahtu E,Heikkila J.Object Classification with Multi-scale Autoconvolution[C]//Proceedings of the 17th International Conference on Pattern Recognition.New York, USA:[s.n.],2004,37-40.

[11] 孙权森,曾生根,王平安,等.典型相关分析的理论及其在特征融合中的应用[J].计算机学报,2005, 28(9):1524-1533.

[12] 刘向增,田 铮,温金环,等.基于仿射不变SIFT特征的SAR图像配准[J].光电工程,2010,37(11): 121-127.

[13] Pankov S.Learning Image Transformations without Training Examples[C]//Proceedings of the 7th International Conference on Advances in Visual Computing. Monte Carlo,Monaco:[s.n.],2011:168-179.

编辑 刘 冰

SAR Image Registration Method Based on Improved SIFT

ZHANG Xiongmei,YI Zhaoxiang,CAI Xingfu,SONG Jianshe
(The Second Artillery Engineering University,Xi’an 710025,China)

Aiming at the problem of Scale Invariant Feature Transform(SIFT)achieving low precision when registating SAR images,an image registration method based on improved SIFT is proposed.Based on the construction of SIFT descriptors and the Multi-scale Autoconvolution(MSA)affine invariant moments of the region around keypoints, Canonical Correlation Analysis(CCA)based fusion method is adopted to fuse them together.The control points are rough matched by using threshold and the distance as well as gray correlation around the matched points are used to construct the similarity matrix.The Singular Value Decomposition(SVD)method is subsequently adopted to implement image registration precisely.The parameters of affine transformation are calculated and the images are registrated.Experimental results show that the registration results of this method is better than SIFT method and achieves precision in sub-pixel level.

SAR image registration;Scale Invariant Feature Transform(SIFT);Multi-scale Autoconvolution(MSA); Canonical Correlation Analysis(CCA);Singular Value Decomposition(SVD)

1000-3428(2015)01-0223-04

A

TP751

10.3969/j.issn.1000-3428.2015.01.041

国家自然科学基金资助重点项目(61132008)。

张雄美(1983-),女,讲师、博士,主研方向:SAR图像处理;易昭湘、蔡幸福,讲师、博士;宋建社,教授、博士生导师。

2013-11-29

2014-02-23 E-mail:zxw.of@163.com

中文引用格式:张雄美,易昭湘,蔡幸福,等.基于改进SIFT的SAR图像配准方法[J].计算机工程,2015,41(1):223-226.

英文引用格式:Zhang Xiongmei,Yi Zhaoxiang,Cai Xingfu,et al.SAR Image Registration Method Based on Improved SIFT[J].Computer Engineering,2015,41(1):223-226.