基于距离度量学习的集成谱聚类

牛 科,张小琴,贾郭军

(山西师范大学数学与计算机科学学院,山西临汾041004)

基于距离度量学习的集成谱聚类

牛 科,张小琴,贾郭军

(山西师范大学数学与计算机科学学院,山西临汾041004)

无监督学习聚类算法的性能依赖于用户在输入数据集上指定的距离度量,该距离度量直接影响数据样本之间的相似性计算,因此,不同的距离度量往往对数据集的聚类结果具有重要的影响。针对谱聚类算法中距离度量的选取问题,提出一种基于边信息距离度量学习的谱聚类算法。该算法利用数据集本身蕴涵的边信息,即在数据集中抽样产生的若干数据样本之间是否具有相似性的信息,进行距离度量学习,将学习所得的距离度量准则应用于谱聚类算法的相似度计算函数,并据此构造相似度矩阵。通过在UCI标准数据集上的实验进行分析,结果表明,与标准谱聚类算法相比,该算法的预测精度得到明显提高。

数据挖掘;边信息;相似度矩阵;距离度量学习;谱聚类;UCI数据集

1 概述

聚类是数据挖掘技术的一种重要手段,旨在将集合中的数据对象分组成不同的类别,使不同的类别之间呈现出高内聚低耦合的特点。

事实上,聚类是一种无监督分类,它没有任何先验知识可用[1],因此,数据对象之间的距离度量对聚类算法的表现性能具有重要影响。合理的距离度量能够准确地反映出数据集中数据对象之间的相互关系,从而提升聚类算法的表现性能,使聚类结果更合理客观的呈现出数据集中数据对象的所属类别及其之间的相互关系。

谱聚类是建立在谱图理论基础上的一种聚类算法。与传统的聚类算法相比,谱聚类能够在任意形状的样本空间上进行聚类且收敛于全局最优解[2],并且使用线性代数基本知识即可实现。

文献[3]提出利用抽样数据样本的相似性作为边信息进行距离度量学习的方法,从而使距离度量能够更加合理地刻画出该数据集中数据样本之间的相互关系,并将其应用 k-means和 Comstrained k-means聚类算法中,使算法的预测精度得到了显著提高。

本文利用数据集抽样样本的相似性作为边信息进行距离度量学习,并且将学习所得的距离度量应用于谱聚类算法。

2 基于边信息的距离度量学习

聚类是一种无监督的机器学习算法,所谓的相似性边信息也就是从数据集中随机抽取出来的一些数据样本以及数据样本之间所属类别的相互关系。

设现有数据集X={xi}⊆Rn,i=1,2,…,n,从X中随机取出一些数据样本,并确认数据样本xi与xj是否具有某种相似性,即数据样本xi与xj否属于同一类别。若xi与xj属于同一类别,则(xi,xj)∈S,否则(xi,xj)∈DS。对于采集到的边信息,本文使用矩阵SC,DC进行描述如下:

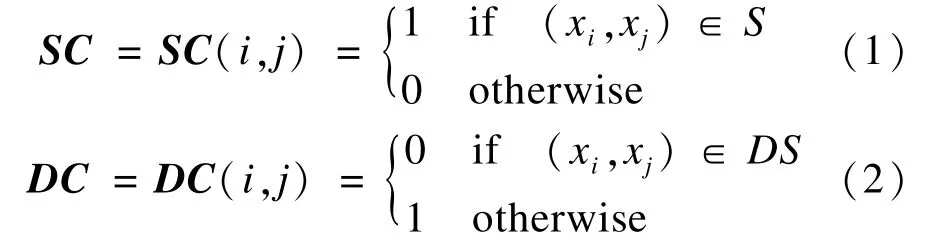
其中,i,j=1,2,…,N,N为随机抽取的数据样本个数。

假设利用抽样样本相似性边信息进行学习所得距离度量具有如下所示的马氏距离[4-5]形式:

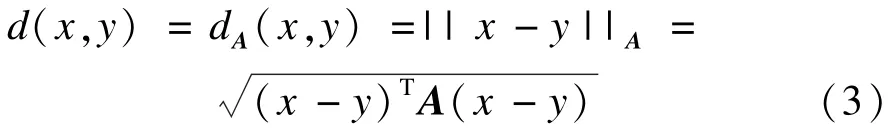
其中,为了保证d(x,y)能够满足非负性和三角不等式,A必须是一个半正定的矩阵。

若A=I,则d(x,y)即为标准欧氏距离;若A是一个对角阵,则相当于对数据样本的每一个维度赋予了不同的权值。更广泛地说,d(x,y)是Rn上的一个使用矩阵A参数化了的马氏距离。

文献[3]提出,求解矩阵A的一种可行方法就是规定集合S中的数据点对(xi,xj)之间具有最小的距离和。而集合DS中的数据点对(xi,xj)之间的距离大于等于1且矩阵A满足半正定。因此,可以通过求解如下凸优化问题,得到矩阵A:

此时,可以使用Newton-Raphson方法,定义:

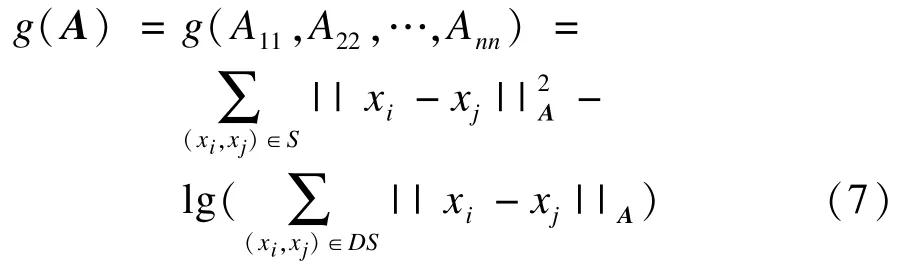
在约束条件A≥0下最小化g对式(7)进行求解,即可以得到一个对角矩阵A。

若使学习所得的矩阵A为全矩阵,可以使用梯度下降和迭代预测算法,求解如下与式(4)～式(6)等价的凸优化问题,即可得到全矩阵A:

梯度下降和迭代预测算法[3]如下:

其中,||M||F表示M的F范数

本文实验的距离度量学习采用Newton-Raphson方法,所得的矩阵A为对角矩阵。

3 谱聚类算法

谱聚类是近年来机器学习领域的一个新的研究热点,基于谱图理论的谱聚类已逐渐成为最为广泛使用的聚类算法之一。在计算机科学、统计学、物理学等领域越来越受到人们的关注[5]。与传统的 kmeans等聚类算法相比,谱聚类在复杂形状样本空间聚类中表现出了良好的性能。

标准谱聚类算法的实现主要依赖于数据集中数据样本的相似度矩阵S=Rn×n、连接矩阵W=Rn×n和度矩阵D=Rn×n。

在谱聚类中通常采用高斯函数计算数据点之间的相似度[6]:

通常将相似度矩阵S采用ξ-近邻、k-近邻、全连通3种方式进行稀疏化处理即可得到连接矩阵W,wij≥0,i,j=1,2,…,n且wij=wji。

度矩阵D则由下式计算所得:

由连接矩阵W和度矩阵D可以得到顶点集的拉普拉斯矩阵[7]。拉普拉斯矩阵分为非归一化和归一化2种。非归一化的拉普拉斯矩阵计算公式如下:

归一化的拉普拉斯矩阵计算公式如下:

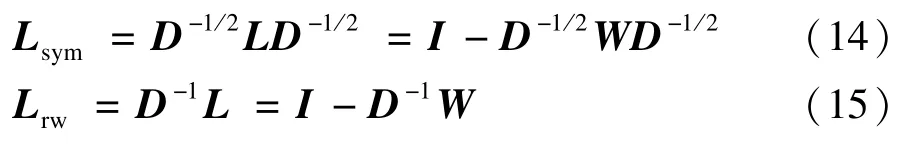
其中,式(14)和式(15)中的L即为式(13)中的非归一化拉普拉斯矩阵。Lsym是对称矩阵,Lrw是一个随机游走矩阵,通常是非对称的[6]。

传统谱聚类算法就是在构建的拉普拉斯矩阵中,根据聚类个数k,求解其前k个特征值以及与其对应的特征向量并构建特征向量空间。然后采用k-means算法对特征向量空间中的特征向量进行聚类[8]。算法步骤描述如下:

输入数据集X={xi}⊆Rn,i=1,2,…,n

输出聚类结果C1,C2,…,Ck

本研究结果提示,应用利培酮对精神分裂进行治疗,能有效改善患者精神症状,且不良反应轻,但可导致患者血脂异常及泌乳素水平上升。因此,在应用利培酮对精神分裂症患者进行治疗的过程中,需针对患者血脂和泌乳素实施定期的监测,加强相关危险因素方面的评估。

Step1构造基于样本间相似度的相似度图,并计算加权连接矩阵W,度矩阵D。

Step2计算拉普拉斯矩阵L(依据需要解决的实际应用问题采用非归一化的拉普拉斯矩阵或者归一化的拉普拉斯矩阵Lsym或者Lrw)。

Step3计算拉普拉斯矩阵L的前k个特征值及其对应的特征向量v1,v2,…,vn(k为需要将数据集进行聚类的个数)。

Step4采用经典的k-means[9-10]聚类算法对特征向量空间的特征向量进行聚类,得到聚类结果C1,C2,…,Ck。

4 基于距离度量学习的谱聚类算法

在基于相似性边信息进行距离度量学习的谱聚类算法中,将学习所得的距离度量d(x,y)应用于谱聚类算法的相似度计算函数,构造数据集的相似度矩阵S。数据样本xi和xj的相似度采用如下公式进行计算:

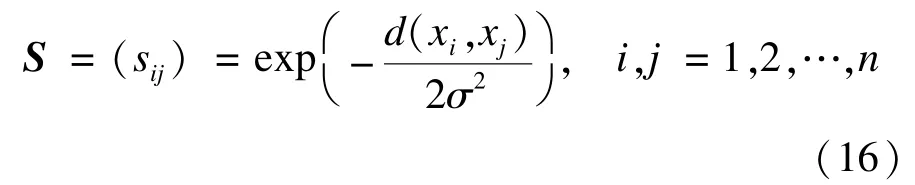
文献[3]提出学习这样的一个距离度量等价于寻找数据样本的一种缩放尺度,即使用A1/2x替代数据样本x,然后再在缩放后的数据集上使用标准的欧氏距离作为距离度量。

基于边信息进行距离度量学习的谱聚类算法步骤如下:

输出聚类结果C1,C2,…,Ck

Step1从数据集X={xi}⊆Rn,i=1,2,…,n中随机抽取N(N＜n)个样本,记为样本Y={yi}⊆Rn,i=1,2,…,N。

Step2通过识别判断集合Y中的数据点(yi,yj),i,j=1,2,…,N是否属于同一类别,从而得到相似性边信息矩阵SC,DC。

Step3利用相似性边信息进行距离度量学习,得到距离度量公式d(x,y)。

Step4利用学习所得的距离度量公式,计算数据点之间的相似度矩阵S。

Step5计算连接权矩阵W和度矩阵D。

Step6计算拉普拉斯矩阵L(依据需要解决的实际应用问题采用非归一化的拉普拉斯矩阵或者归一化的拉普拉斯矩阵Lsym或者Lrw)。

Step7计算拉普拉斯矩阵L的前k个特征值及其对应的特征向量v1,v2,…,vn(k为需要将数据集进行聚类的个数)。

Step8采用经典的k-means[9-10]聚类算法对特征向量空间的特征向量进行聚类,得到聚类结果C1,C2,…,Ck。

5 实验结果与分析

5.1 实验平台

本文所有实验都是在1台PC机(Intel Core i3 CPU,主频2.40 GHz,内存2.0 GB)上进行。采用Windows XP SP3操作系统,Matlab R2009a开发平台。

5.2 结果分析

为了验证本文提出的使用数据集抽样样本相似性边信息进行距离度量学习的谱聚类算法的有效性,分别在5个UCI[11]标准数据集上进行了实验,并将聚类结果与标准的谱聚类算法进行了比较。

各个数据集的属性如表1所示。

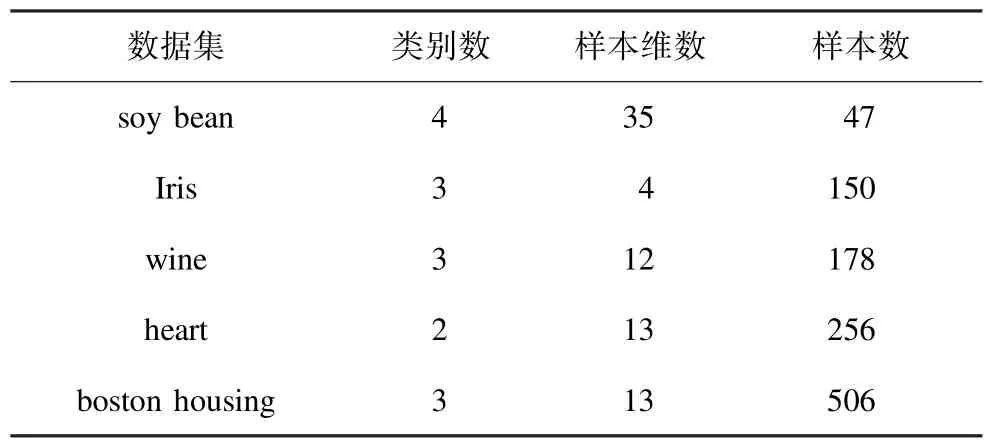
表1 各个UCI标准数据集的属性

在实验中采用聚类精度作为评价指标。分别在各个数据集中随机抽取 5个、10个、15个、20个、25个、30个数据样本,并判断各样本的所属类别的相互关系作为相似性边信息进行距离度量学习。实验使用Hungarian算法[12]进行聚类精度计算。

各数据集实验结果如表2所示。

表2 UCI数据集实验结果对比

图1～图5为各个UCI标准数据集实验对比结果。

图1 数据集soy bean实验结果对比

图2 数据集Iris实验结果对比

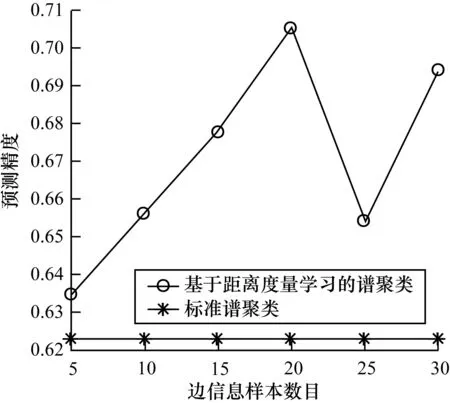
图3 数据集wine实验结果对比

图4 数据集heart实验结果对比

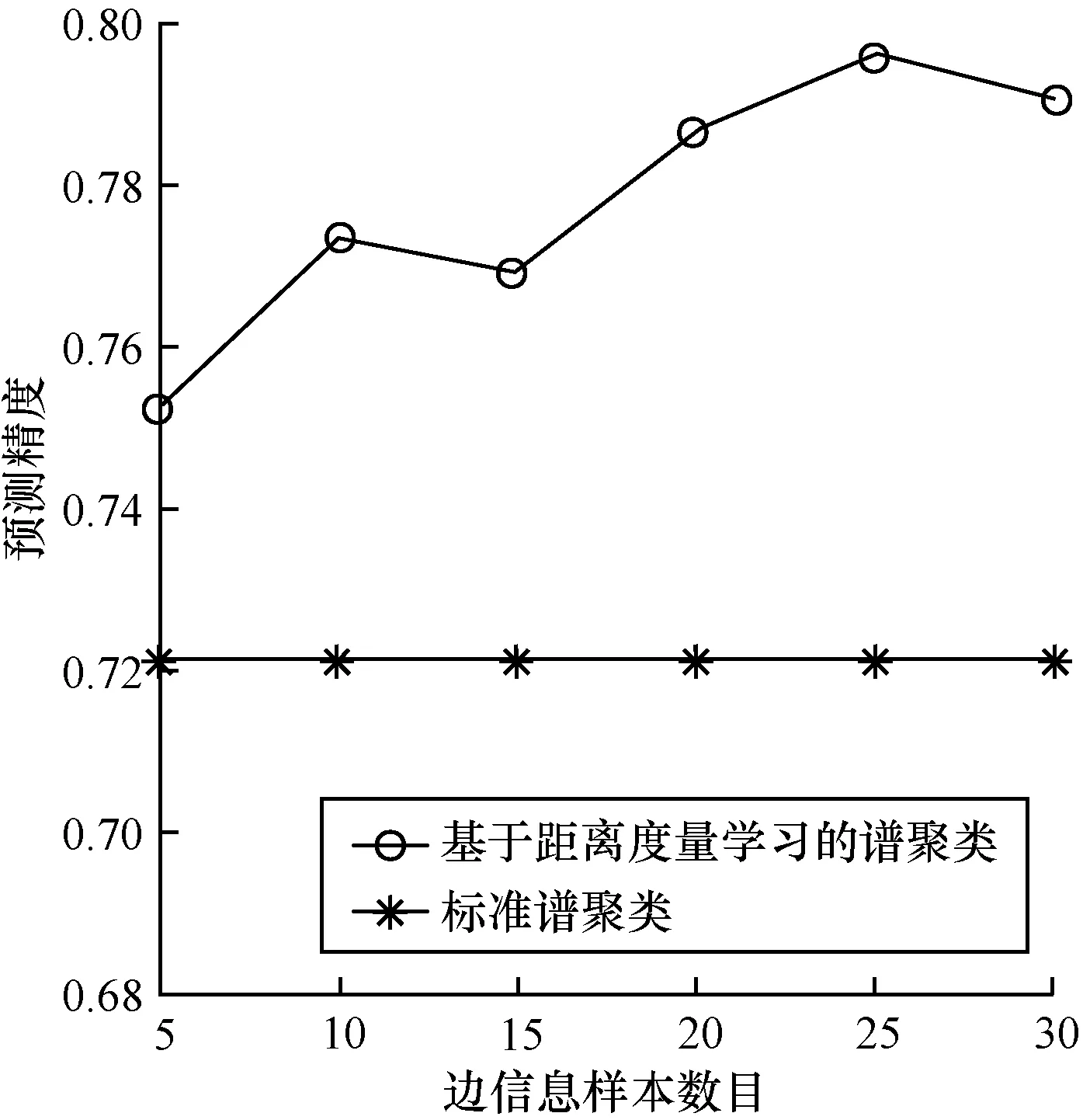
图5 数据集boston housing实验结果对比

通过对比分析可得,与标准谱聚类算法相比,利用数据集抽样样本相似性边信息进行距离度量学习的谱聚类算法的聚类性能得到了显著提高。然而,随着数据集相似性边信息的增多,聚类的性能并不会成正比例上升。

6 结束语

本文提出一种利用数据集抽样样本相似性边信息进行距离度量学习的谱聚类算法。实验结果表明,与标准谱聚类算法相比,该算法的聚类性能得到了明显改善。在执行谱聚类算法时,高斯相似度函数中的参数σ选取的是否合理,也会对聚类结果产生重要的影响。因此,参数σ的选取是下一步需要研究的工作。

[1] 孙吉贵,刘 杰,赵连宇.聚类算法研究[J].软件学报,2008,19(1):48-61.

[2] 蔡晓妍,戴冠中,杨黎斌.谱聚类算法综述[J].计算机科学,2008,35(7):14-18.

[3] Eric P,Andrew Y,Michael I.Distance Metric Learning with Application to Clustering with Side-information[C]// Proceedings of NIPS’02.Vancouver,Canada:[s.n.], 2002:505-512.

[4] 张尧庭,方开泰.多元统计分析引论[M].北京:科学出版社,1982.

[5] 张 翔,王士同.一种基于马氏距离的可能性聚类方法[J].数据采集与处理,2011,23(8):86-88.

[6] Luxburg U.A Tutorial on Spectral Clustering[J].Satictics and Computing,2007,17(4):395-416.

[7] Fiede M.Algebraic Connectivity of Graphs[J].Czechoslovak Math,1973,23(2):298-305.

[8] Ng A Y,Jordan M I,Weiss Y.On Spectral Clustering: Analysis and an Algorithm[C]//Proceedings of NIPS’01. Vancouver,Canada:[s.n.],2001:849-856.

[9] 张建辉.K-means聚类算法研究及应用[D].武汉:武汉理工大学,2007.

[10] 王 千,王 成,冯振元,等.K-means聚类算法研究综述[J].电子设计工程,2012,20(7):21-24.

[11] UC Irvine. UC Irvine Machine Learning Repository[EB/OL].(2012-11-21).http://archive.ics.uci. edu/ml/index.html.

[12] Kuhn H W.The Hungarian Method for the Assignment Problem[J].Naval Research Logistics Quarterly,1955, 2(1/2):83-97.

编辑 刘 冰

Integrated Spectral Clustering Based on Distance Metric Learning

NIU Ke,ZHANG Xiaoqin,JIA Guojun
(School of Mathematics and Computer Science,Shanxi Normal University,Linfen 041004,China)

The performance of the unsupervised learning clustering algorithm is critically dependent on the distance metric being given by a user over the inputs of the data set.The calculation of the similarity between the data samples lies on the specified metric,therefore,the distance metric has a significant influence to the results of the clustering algorithm. Aiming at the problem of the selection of the distance metric for the spectral clustering algorithm,a spectral clustering algorithm based on distance metric learning with side-information is presented.The algorithm learns a distance metric with the side-information.The similarity between the data samples is chosen randomly from the data set,and is applied to the similarity function of spectral clustering algorithm.It structures the similarity matrix of the algorithm.The effectiveness of the algorithm is verified on real standard data sets on UCI,and experimental results show that compared with the standard spectral clustering algorithms,the prediction accuracy of the proposed algorithm is improved significantly.

data mining;side-information;similarity matrix;distance metric learning;spectral clustering;UCI data set

1000-3428(2015)01-0207-04

A

TP18

10.3969/j.issn.1000-3428.2015.01.038

山西省软科学基金资助项目(2009041052-03)。

牛 科(1987-),男,硕士研究生,主研方向:智能计算,软件工程;张小琴,硕士研究生;贾郭军,副教授。

2013-10-31

2014-03-03 E-mail:niuke870505@163.com

中文引用格式:牛 科,张小琴,贾郭军.基于距离度量学习的集成谱聚类[J].计算机工程,2015,41(1):207-210.

英文引用格式:Niu Ke,Zhang Xiaoqin,Jia Guojun.Integrated Spectral Clustering Based on Distance Metric Learning[J]. Computer Engineering,2015,41(1):207-210.