翼伞发电系统的GPU并行轨迹优化

张利民, 孙明玮, 刘东辉, 全胜, 陈增强

(1.辽宁工程技术大学机械工程学院,辽宁阜新,123000;2.南开大学计算机与控制工程学院,天津300071;3.北京机电工程研究所,北京100074)

翼伞发电系统的GPU并行轨迹优化

张利民1, 孙明玮2, 刘东辉2, 全胜3, 陈增强2

(1.辽宁工程技术大学机械工程学院,辽宁阜新,123000;2.南开大学计算机与控制工程学院,天津300071;3.北京机电工程研究所,北京100074)

高空风能发电是一种新型的清洁能源生产方式。针对这种非常规的带有特定目标函数优化的轨迹设计问题,采用预测控制是一条可行途径,但该方法目前需要事先离线求解,计算量极大,不具有在线自适应能力。提出了一种基于混沌的实时轨迹优化策略,以克服上述算法的不足。这是一维变量滚动次优化问题,利用均匀采样结合混沌搜索,给出了过程约束下的优化方法。通过采用数值算法的并行化,提高了在线计算效率。半实物仿真试验结果说明了该算法的有效性。

翼伞发电系统;轨迹优化;滚动时域;混沌;图像处理器;并行计算

0 引 言

由于地面上的风极不稳定,导致了风力发电中地面发电机组风轮转速的不稳定,使得传统风电被称为“垃圾电”［1］。与此对照,高空风速不仅大而且方向稳定,具有弥补上述不足的潜力。最近几年欧洲等国的一些学者,提出了一种全新的风力发电概念:借助高空风能利用翼伞(或者风筝)进行发电［2］。人们对这种新型风力发电装置寄予厚望。翼伞风力发电系统的原理很简单:通过绳索牵引一个翼伞,来操纵翼伞的飞行机动,并带动发电机运转以取得能量输出,或者驱动电动机将翼伞牵引回来。翼伞的每个运动轨迹周期包括2个部分:在发电阶段,绳长增加,执行结构为发电机输出电能;当绳长接近最大值时,则转换为回收阶段,绳长减小,执行结构为电动机消耗电能［3］。

显然,作为一个发电系统,经济效益也就是单位时间的发电功率是一个关键指标。翼伞发电系统在这方面有其独到的特点:通过设计一定的飞行轨迹,使得净发电量最大,同时满足一定的过程约束。以发电量为指标的轨迹设计与传统飞行器设计中以位置为核心的轨迹制导存在很大的差异。这是一个非线性最优控制问题。针对实际工程中最优控制难以实施的不足,一种次优化滚动时域控制(receding horizon control,RHC)算法,也就是模型预测控制(model predictive control,MPC)被提出,在20世纪80年代初期以来,得到迅速发展［4-6］,并已在大量过程工业中得到应用,取得了良好的经济效益［7,8］。预测控制的一大优势是可以直接处理各种过程约束。基于线性模型的预测控制比较成熟,但是对于非线性模型的预测控制无论是理论研究还是实际应用都比较困难［9,10］。文献［11］给出了一种快速非线性预测控制算法,并将该算法应用于高空风筝风能发电的轨迹优化设计中［3,12］;但该方法需要事先离线计算好上万个状态点的预测控制输出,实际使用时进行插值,存在如下不足:离线计算量极大,优化精确度难以保证;当气动参数(升、阻力系数)发生明显变化时,如在方案论证选型阶段或者实际飞行气动参数辨识后发现与原标称值差异较大时,算法的优化效果将大打折扣,需要重新进行离线计算,适应性、灵活性和可扩展性严重不足。这些都给离线预测控制算法的应用带来了障碍。

本文主要在非线性预测控制应用于翼伞发电系统方面进行了优化。在算法设计方面,给出翼伞发电系统轨迹优化设计的在线滚动时域方法。将目标函数转化为一个单变量函数关系。设定不同的指令更新周期与预测控制解算积分步长,提高运算速度。将具有过程约束的函数优化转化为具有双重优先级的序列排序问题,利用有限区间的全局均匀采样结合局部极值点附近的混沌优化搜索,在线确定出满足滚动时域的最优控制量。在算法实现方面,采用了CPU+GPU(Graphical Processing Unit)的异构计算模式,通过并行方式提高了搜索优化算法的计算效率。半实物仿真试验验证了本文算法的有效性。

1 问题描述

1.1 翼伞发电系统的动力学模型

牵引翼伞动力学见文献［12、13］。这是一种双绳索牵引装置,分别联结在翼伞的前、后缘处,并且假设翼伞不变形,2个联结点之间的距离是d,而2根绳长之差为Δl,它也就是驱动翼伞轨迹发生改变的控制量。假设地面坐标系(X,Y,Z),原点位于牵引绳的固定点处,而风速方向与X轴平行。标称风速向量表示为

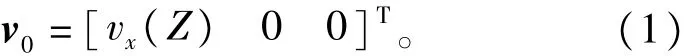
式中vx(Z)为已知的与高度相关的标称风速。实际风速向量为

式中vt为风场扰动向量。牵引翼伞动力学模型为

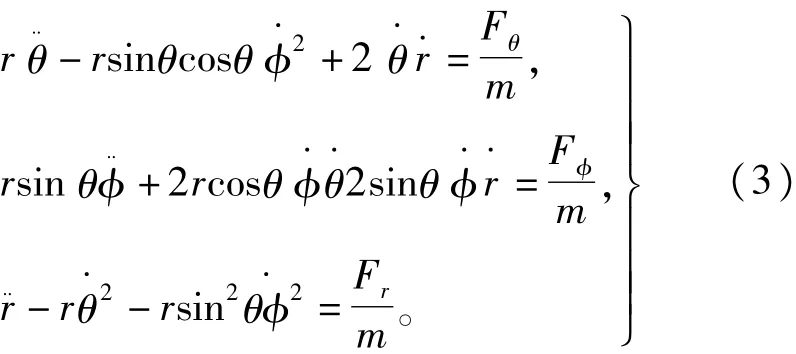
式中:r表示牵引绳长;θ为位置俯仰角;ψ为位置航向角;m为翼伞质量,而翼伞所受外力在3个极坐标系方向上的分量为:

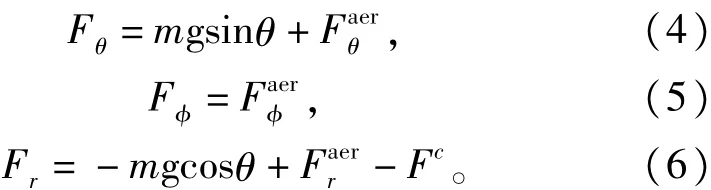
式中Fc为牵引力。而气动力在3个方向的分力为:

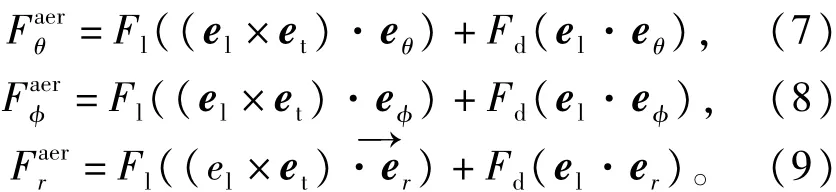
这里升力为

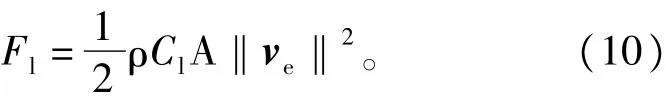
阻力为式中:ρ为空气密度;A为翼伞参考面积;Cl、Cd分别是升、阻力系数;空速向量为

翼伞的位置向量为

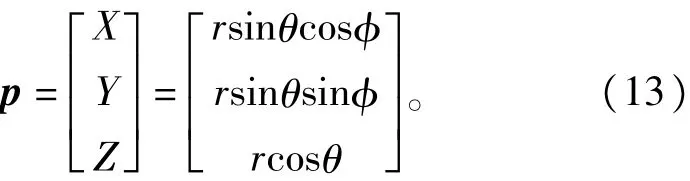
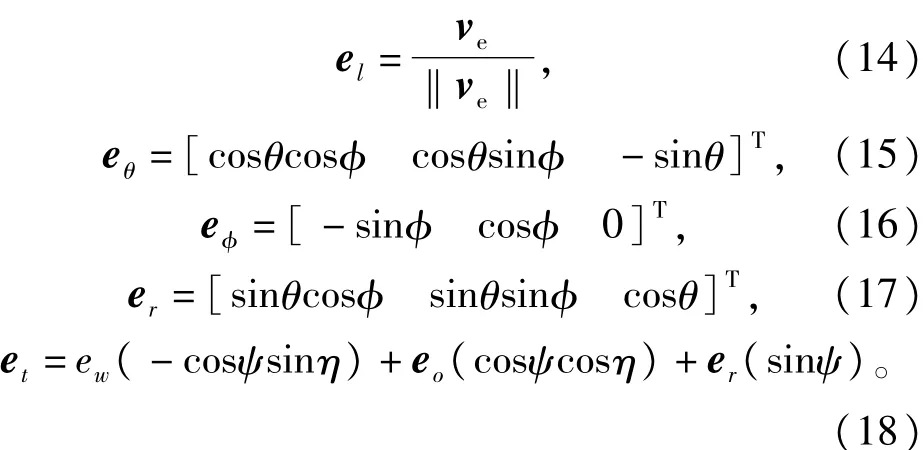
其中:

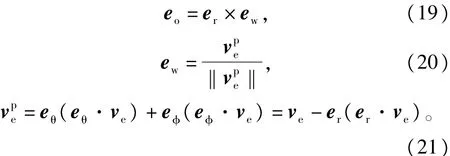
而式(7)～式(9)中的几个单位向量定义为

而

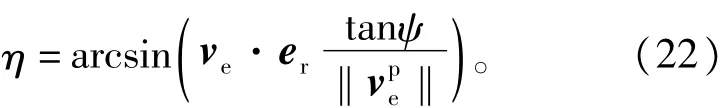
这里ψ就是控制变量,定义为

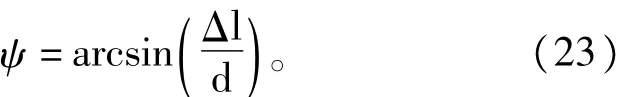
显然需要满足

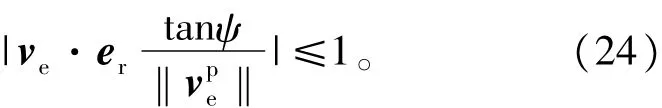
当绳长增加时,发电机输出功率为

当绳长减小时,电动机消耗功率为

1.2 约束条件

为了保证整个运行期间翼伞不发生撞地,需要满足

控制变量需要满足绝对值和速率约束:

1.3 目标函数

翼伞发电系统以追求单位时间内的发电净功率最大为目标。由于翼伞纯发电出现在牵引绳长增加阶段,这一阶段时间应尽可能长,发电功率最大应为指标;而在绳长超过一定限度后,绳长需要减少,此时电动机消耗功率,应该使这一阶段尽可能短,消耗功率最小应为指标;而在这两个阶段中间的过渡阶段,则需要保证俯仰角和航向角一定的方位条件,以使得发电阶段能够充分利用风能。整个过程可以分为4个阶段,详细可参见［13］。

1)绳长伸长发电阶段。

这个阶段的主要目标是产生尽可能多的电能,因此目标函数是

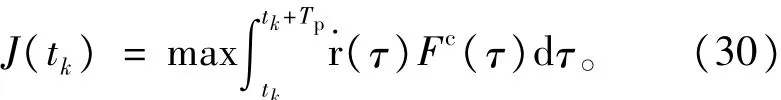
式中Tp为向前预测的时域长度。这一阶段结束,转入绳长回收阶段Ⅰ。

2)绳长回收阶段Ⅰ。

这一阶段的主要目标是使得θ变小,而｜φ｜增大,以便于回收阶段的电动机功率消耗比较小。因此,目标函数是

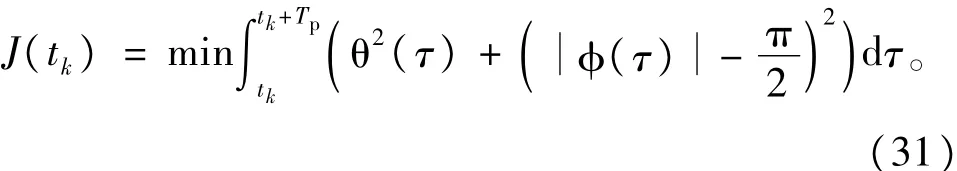
这一阶段结束,转入绳长回收阶段Ⅱ。

3)绳长回收阶段Ⅱ。

这个阶段是回收的主要阶段,需要消耗功率,所以目标函数是

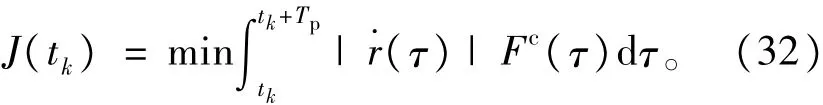
这一阶段结束,转入绳长回收阶段Ⅲ。

4)绳长回收阶段Ⅲ。

这一阶段的主要目标是使得翼伞再进入发电阶段,因此目标函数是

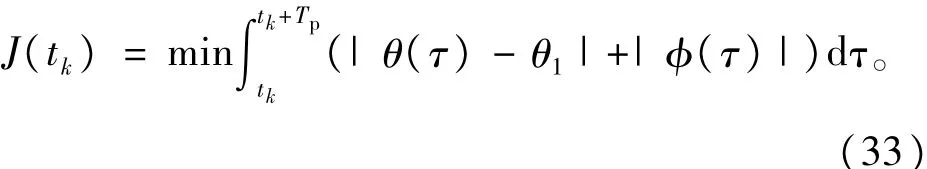
2 滚动时域控制方法

2.1 基本原理

模型预测控制采用的滚动时域优化思想是一种次优化策略。考虑如下的动力学模型

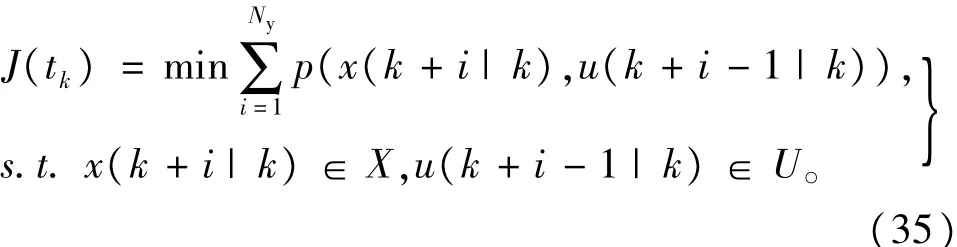
式中:x∈Rn为系统状态;u∈Rm为控制量。第tk时刻的目标函数定义为式中:p(·,·)为特定泛函;x(k+i｜k)和u(k+i-1｜k)分别为状态和控制预测值;Ny为预测时域长度;X和U分别是对于状态与控制变量的约束范围。在每一个采样间隔内,求解满足约束的最

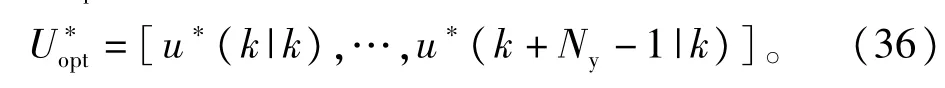
优U*并仅将第一个分量u(k｜k)投入闭环控制。在下一个采样周期,重复上述步骤。需要说明的是,一般情况下目标函数(35)采用二次型的形式,而如果此时动力学模型(34)是线性定常系统,并且不存在不等式约束,则可以得到闭环解析解。对于本文的情形,分段目标泛函(30)、(31)、(32)和(33)都不是状态的二次型,并且由于动力学方程(3)的非线性特性以及多种过程及控制不等式约束的存在,显然不存在解析解。

2.2 数值优化方法

除了极少数的线性系统,预测控制的求解基本上无法直接得到解析解。对于非线性系统的约束预测控制,一般都采用数值求解算法,也就是非线性规划的算法。可以通过引入控制时域参数Nu来降低计算复杂性,也就是当i＞Nu时,控制量保持恒定,即

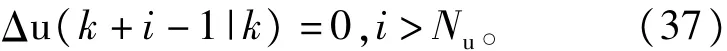
取Nu=1,就可以将问题转化为一个一维搜索问题,极大地简化了求解过程。

由于本问题包含有过程约束,因此在搜索过程中对于目标函数的大小判断应该包含两个层次:首先考虑约束的满足情况;其次才考虑目标泛函的具体值。翼伞发电系统的主要约束是避免撞地,本文采用每个滚动时域内约束被破坏次数Nc越少的控制量优先级越高的方式;在此优先级相同的情况下,再考虑目标函数的具体取值。因此,整个问题可以转换为对于一个具有二重优先级的数组进行寻优的问题,其中第一级变量是离散的整数,而第二级变量是连续的实数。这种方法对于具有过程约束的优化问题进行了有效转换。

本文采用全局均匀采样附加局部最优点附近的Tent混沌精搜索策略,确定出不同控制变量的最优性。

设在每一时刻k,根据控制约束(28)和(29)得到的可行控制量区间为［ψmin(tk),ψmax(tk)］,在此区间中进行均匀采样,总采样个数为Ns,得到均匀采样点序列ψs(k,i)(i=1,2,…,N)。对于每一个i (1≤i≤N),对于确定的预测控制解算积分步长Tc,固定t0=kTc到tf=(k+Ny-1)Tc时刻的控制量为ψs(k,i),通过数值积分方法得到对应的约束破坏次数Nc和目标函数值J(ψs(k,i)),并进行双优先级排序。确定出其中所有的局部极小点所在的子区间,将每一子区间内唯一的采样点标记为il(l=1, 2,…,Nl),其中Nl是判断出的子区间的个数。

对于每一个局部极小点所在子区间［ψi-1, ψi+1］,进一步采用混沌搜索策略进行精搜索。混沌具有独特的遍历性,即混沌能在一定范围内按其自身的规律永不重复地遍历所有状态,这种特性可作为在优化搜索过程中避免陷入局部极小、实现全局优化的一种机制。混沌优化方法具有良好的全局寻优能力,而且由于其搜索过程完全按混沌运动自身的规律和特性进行,因而获得最优解的可能性更强,而且结构简单、容易实现,是一种极有前途的优化手段,并且已经成功应用在非线性预测控制的优化求解上［14］。本文采用文献［15］中提出的Tent映射进行混沌优化搜索。Tent映射又称为二进制移位映射,定义为

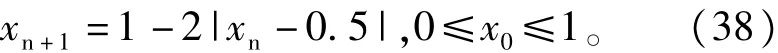
可以证明当初始值x0为无理数时,Tent映射可以遍历区间［0,1］,并且概率分布函数是均匀的。混沌优化的步骤如下:

1)确定初始值0≤x0≤1为无理数,n=0,确定混沌优化迭代次数为Ni。

2)按照式(45)计算出xn+1,载波映射到期望区间中的对应控制量

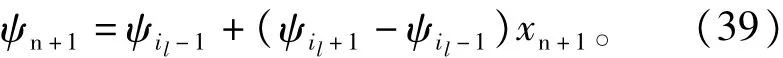
并计算出约束破坏次数Nc(ψn+1)和J(ψn+1), n=n+1。

3)当n＜Ni时,返回2);否则跳转4)。

4)对于二元序列{Nc(ψi),J(ψi)}(i=1,2,…, N)进行优先级排序,确定出该序列中的最小值。

这样就完成了对于该子区间的精搜索。对于所有的含有局部极小点的子区间进行上述混沌精搜索,选取它们中的最小值,并与边界值进行比较,以确定整个区间中的最优值。

3 轨迹优化设计方法的并行实现

3.1 GPU并行计算原理

由于翼伞系统是一种复杂的非线性模型,而本文采用的非线性预测控制算法核心就是对于每一个采样点进行向前的动力学解算预测,这其中包含很多非线性函数,使得计算量比较大。提高实用性的关键点就是提高在线运算速度。由于本文算法的采样特点具有很明显的可并行化特性,可以充分应用GPU进行计算。目前许多大规模电力计算和优化问题都十分适用GPU进行并行处理［16］。

目前,基于GPU的并行计算一般是在CUDA (Compute Unified Device Architecture)环境下进行。虽然CUDA目前只能支持NVIDIA公司的GPU,但它是目前最成熟、实用化程度最高的通用计算架构,而且它的编程模型也最适合充分发挥GPU的并行计算能力。在CUDA的编程模型中采用CPU+GPU异构计算模式,CPU负责进行逻辑性较强的事务处理和串行计算,GPU负责执行高度线程化的并行处理任务［15］。一个CUDA程序包含有主机端(CPU)和设备端(GPU)两部分代码。程序运行时通过在主机端调用kernel函数将具有并行特性的计算任务映射到大量可以在GPU上并行执行的线程上,并且由硬件动态调度和执行这些线程,线程切换时系统开销很小。由此实现了基于GPU的大规模并行计算。

3.2 并行实现策略

在前面所提出的翼伞风力发电系统轨迹优化设计算法中,主要的计算集中在全局均匀采样和局部最优点附近的Tent混沌精搜索两部分,且均明显具有可并行化实现的特性。其中对于未来动力学的解算预测、求解各采样点对应的约束破坏次数和目标函数值,可以将这部分计算转移到GPU上进行。通过在主机端调用一个kernel函数,系统自动创建一个线程网格,它包含有大量可在GPU上并行执行的线程,其中每个线程负责一个采样点的数值计算。在局部小区间内采用基于Tent映射的混沌搜索步骤中,可以先在CPU上迭代出所有的混沌变量,并将它们映射到期望区间相应的控制量,然后将采样点的特定计算转移到GPU并行执行。

4 半实物仿真试验与结果分析

以支持CUDA功能的NVIDIA显卡为基础,搭建了考核并行算法实时性的半实物仿真平台,系统配置如表1所示。

表1 GPU并行环境配置Table 1 Environment configuration for GPU parallel computation

本文以文献［18,20］中的实例进行数值仿真,一些符号的具体意义也可参见［15］。

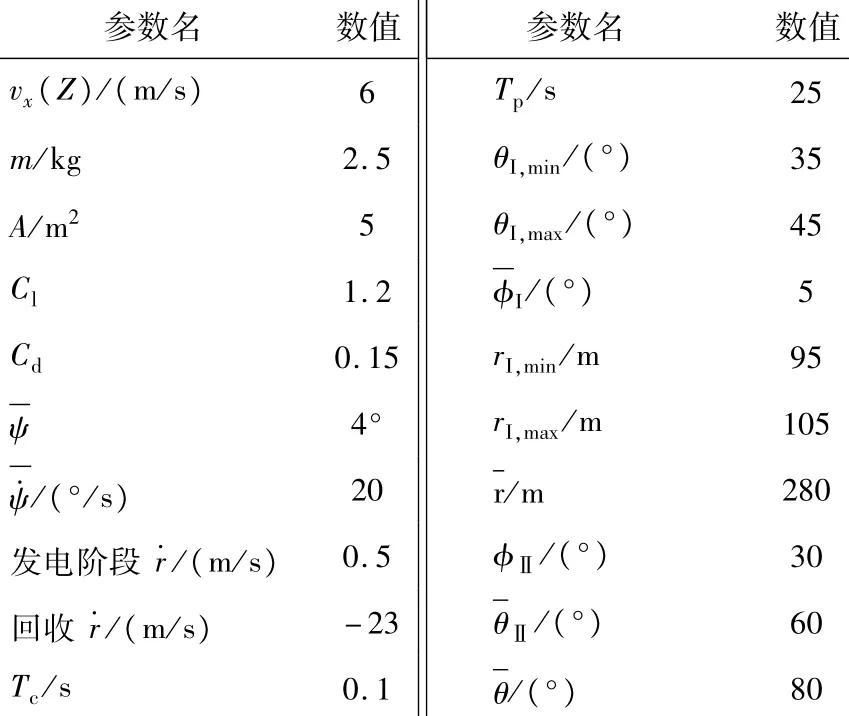
表2 仿真参数设置Table 2 Parameter configuration of the simulation

均匀采样点数为Ns=100,每个局部极小值所在区间混沌优化的迭代次数取为Ni=20。Tent混沌映射的初始值取为无理数x0=1。

由于GPU和CPU的运算单元采用了不同的微架构,GPU的计算精确度低于CPU,因此即使都符合IEEE754规范,计算结果也可能会有差异。因此有必要对CPU串行程序和GPU并行程序的优化结果进行对比,以此判断采用GPU并行加速的程序是否可靠和有效。图1为采用GPU并行加速后优化出的翼伞飞行轨迹。三维位置轨迹显示翼伞在发电阶段处于一种顺风向前的圆周运动之中。在发电阶段,由于圆周间距很小,可以维持很长时间;而在消耗功率的回收阶段,则时间很短。与CPU串行程序相比［13］,一个发电周期内在X、Y、Z三个方向差值的均方都为厘米量级,可知GPU加速后程序的结果与CPU串行程序的结果基本一致,具有可信性。图2和图3分别是俯仰-航向角相平面曲线与输出功率曲线。每个发电周期发电量约为754kJ,比文献［17］中的结果大约提高3%。

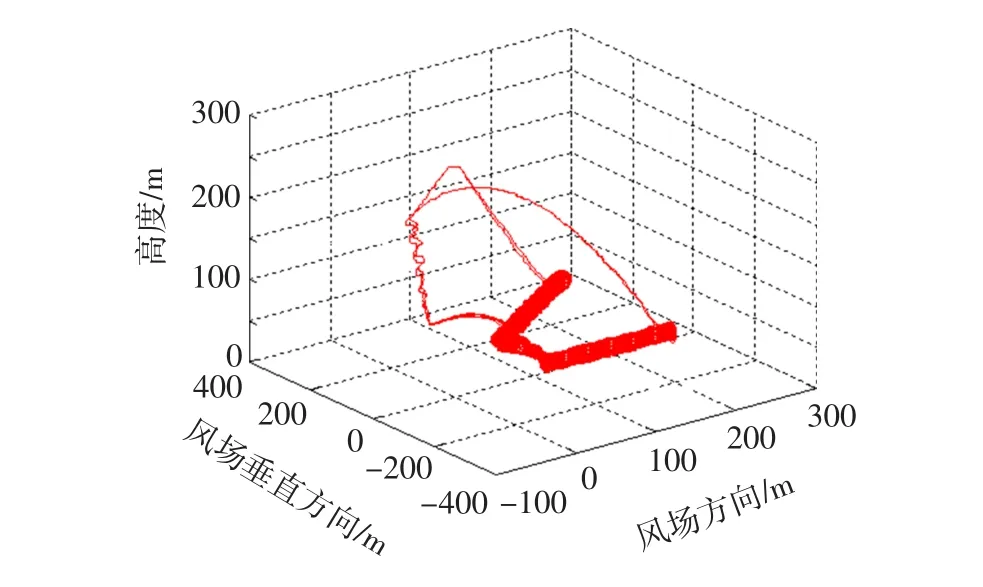
图1 三维轨迹Fig.1 Three-dim ension trajectory

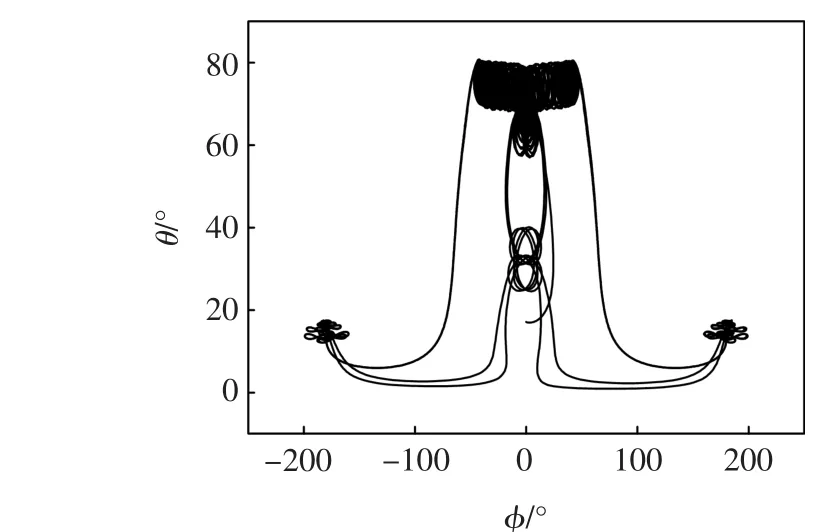
图2 位置俯仰—航向角相平面图Fig.2 Phase plot between pitch and azimuth angle for the positions

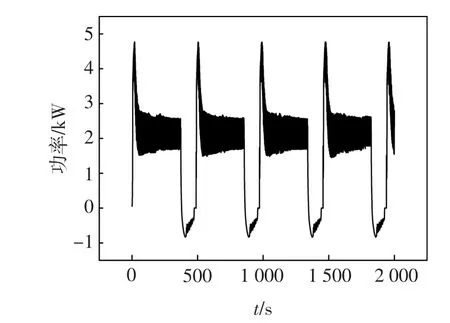
图3 发—耗电功率曲线Fig.3 Generated and dissipated power

为了验证上文中提到的GPU并行方法的加速效果,选取一些不同采样点个数的情况进行一个发电周期内(约500 s)运算速度的对比。实验结果如表3所示。从表3中首先看出,本文设计的算法完全满足了实时性的要求;其次采用GPU并行计算加速后取得了较好的加速效果,采样点个数越多时,加速效果越好。通过结合本文的实际情况,20个采样点的结果已经比较理想了。

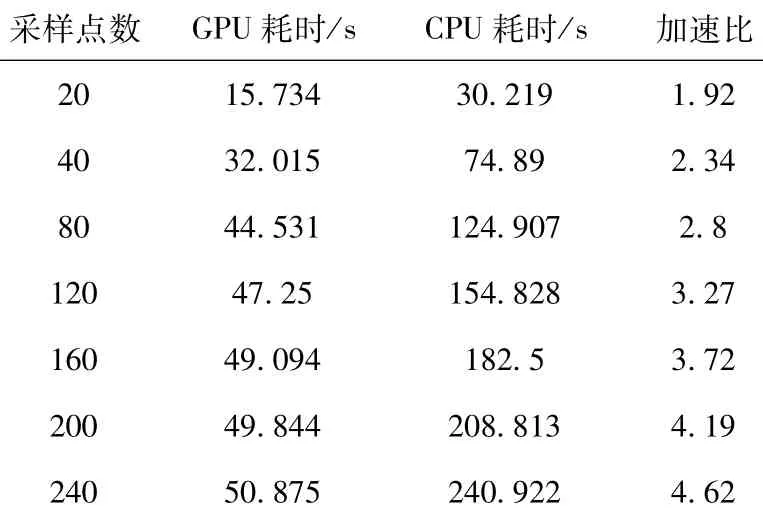
表3 一个发电周期内不同采样点数时程序耗时与加速比Tab le 3 The relation between the calculation time, speedup and the number of samp ling points in each cycle

5 结 论

本文通过综合采用混沌优化与GPU并行计算方式,给出了可以在线实现的翼伞发电系统预测控制轨迹优化方法,克服了原离线方法计算量大,对于系统参数变化不具有灵活扩展能力的问题,可为系统论证提供快速的分析手段。实验室半实物仿真试验结果显示输出功率比原算法有所提高,同时满足实时性要求,说明了算法的有效性。

［1］ 张宏宇,印永华,申洪,等.大规模风电接入后的系统调峰充裕性评估［J］.中国电机工程学报,2011,31(22):26-31. ZHANG Hongyu,YIN Yonghua,SHEN Hong,et al.Peak-load regulation adequacy evaluation associated with large-scale wind power integration［J］.Proceedings of the CSEE,2011,31(22): 26-31.

［2］ THRESHER R,ROBINSON M,Veers P.To capture the wind［J］.IEEE Power Energy Magazine,2007,5(6):34-46.

［3］ CANALEM,FAGIANO L,Milanese M.Power kites forwind energy generation-fast predictive control of tethered airfoils［J］. IEEE Control System Magazine,2007,27(6):25-38.

［4］ CUTLER C R,RAMAKER B L.Dynamic matrix control-a computer control algorithm［C］//The Joint Automatic Control Conference,San Francisco,USA,1980.

［5］ ROUHANIR,MEHRA R K.Model algorithmic control(MAC): basic theoretical properties［J］.Automatica,1982,18(4):401 -414.

［6］ CLARKEDW,MOHTADIC,TUFFSPS.Generalized predictive control［J］.Automatica,1987,23(2):137-160.

［7］ MORARIM,LEE JH.Model predictive control:past,present and future［J］.Computers&Chemical Engineering,1999,23(4 -5):667-682.

［8］ QIN S J,BADGWELL T A.A survey of industrialmodel predictive control technology［J］.Control Engineering Practice,2003, 11(7):733-764.

［9］ HENSON M A.Nonlinearmodel predictive control:current status and future directions［J］.Computers&Chemical Engineering, 1998,23(2):187-202.

［10］ 席裕庚,李德伟.预测控制定性综合理论的基本思路和研究现状［J］.自动化学报,2008,34(10):1225-1234. XI Yugeng,LI Dewei.Fundamental philosophy and status of qualitative synthesis ofmodel predictive control［J］.Acta Automatica Sinica,2008,34(10):1225-1234.

［11］ CANALE M,FAGIANO L,MILANESEM.Setmembership approximation theory for fast implementation of model predictive control laws［J］.Automatica,2009,45(1):45-54.

［12］ CANALE M,FAGIANO L,MILANESE M.High altitude wind energy generation using controlled power kites［J］.IEEE Transactions on Control Systems Technology,2010,18(2):279 -293.

［13］ 孙明玮,刘东辉,全胜,等.翼伞发电系统在线预测控制轨迹优化设计［C］//2012年中国控制会议,合肥,中国:4183 -4188.

［14］ 董娜,陈增强,孙青林,等.基于粒子群优化的有约束模型预测控制器［J］.控制理论与应用,2009,26(9):965-969. DONG Na,CHEN Zengqian,SUN Qinglin,et al.Particalswarm optimization algorithm for model predictive control with constraints［J］.Control Theory&Applications,2009,26(9): 965-969.

［15］ SONG Y,CHEN ZQ,YUAN Z Z.New chaotic PSO-based neural network predictive control for nonlinear process［J］.IEEE Transactions on Neural Networks,2007,18(2):595-600.

［16］ 路飞,田国会,贾磊.用多种群并行自适应遗传算法解混合Flowshop调度问题［J］.电机与控制学报,2002,6(1):68-70. LU Fei,TIAN Guohui,JIA Lei.Solution to hybrid Flowshop scheduling problem using amulti group parallel and adaptive genetic algorithm［J］.Electric Machines and Control,2002,6 (1):68-70.

［17］ CANALEM,FAGIANO L,IPPOLITOM,etal.Controlof tethered airfoils for a new class of wind energy generation［C］//Proceedings of the45th IEEEConference on Decision&Control,December 13-15,2006,San Diego,USA,2006:4020-4026.

(编辑:贾志超)

GPU based trajectory parallel optim ization of tethered airfoils for w ind energy generator

ZHANG Li-min1, SUN Ming-wei2, LIU Dong-hui2, QUAN Sheng3, CHEN Zeng-qiang2
(1.School of Mechanical Engineering,Liaoning Technical University,Fuxin 123000,China;2.College of Computer& Control Engineering,Nankai University,Tianjin 300071,China;3.Beijing Electro-Mechanical Engineering Institute,Beijing 10074,China)

Wind energy at high altitudes is a new approach to generate clean energy.The predictive control in the offlinemanner was previously employed to handle the problem of trajectory design with unconcventionally given objective function,however it is time-consuming and lacks of adaptability and flexibility to varying aerodynamic parameters.A receding horizon optimizationmethod for the tethered foil generator based on an online searching strategy was presented.The nonlinear optimization problem was approximately reformulated to a univariate receding horizon sub-optimal issue in a short interval.By using uniform sampling and chaotic search approaches,the sub-optimal solution,subject to the physical constraints,was obtained.The proposedmethod is parallelly implemented by graphic processing unit(GPU) to raise its online calculation efficiency.The hardware-in-the-loop simulation result demonstrates its effectiveness.

tethered airfoil for wind energy generator;trajectory optimization;receding horizon;chaos; graphical processing unit(GPU); parallel computation

10.15938/j.emc.2015.08.013

TK 89;TP 273;V 448

A

1007-449X(2015)08-0088-07

2013-05-19

国家自然科学基金(61174094,61273138),教育部优秀新世纪人才支持计划研究项目(NCET-10-0506)

张利民(1982—),男,博士,讲师,研究方向为导航制导;孙明玮(1972—),男,博士,副教授,研究方向为飞行器制导控制;刘东辉(1988—),男,硕士研究生,研究方向为导航制导;全 胜(1970—),男,硕士,高级工程师,研究方向为导航制导;陈增强(1963—),男,博士,教授,研究方向为多智能体。

孙明玮