基于新型ADRC控制器和MC变换器的电机DTC控制系统研究

程启明, 黄伟, 程尹曼, 郭凯, 徐聪, 邓亮

(1.上海电力学院自动化工程学院,上海200090;2.上海电力公司市北供电分公司,上海200041)

基于新型ADRC控制器和MC变换器的电机DTC控制系统研究

程启明1, 黄伟1, 程尹曼2, 郭凯1, 徐聪1, 邓亮1

(1.上海电力学院自动化工程学院,上海200090;2.上海电力公司市北供电分公司,上海200041)

针对传统PID控制器参数鲁棒性和杭干扰性均较差的问题,提出了一种基于简化参数的自杭扰控制器(ADRC)的感应电机(IM)直接转矩控制(DTC)方法,它以给定转速和实际转速作为输入信号,并以给定电磁转矩作为输出信号,从而设计了基于简化参数的ADRC速度控制器。另外,由于传统DTC系统中采用常规的矩阵变换器(MC),其电压传输比较低,难以满足电机对电压的要求,直接影响了电机的输出特性,依据三相boost斩波器和MC的优势,提出一种新型MC直接转矩控制(DTC)方法,并对其进行建模分析,从理论上证明了该拓扑结构的合理性。仿真结果表明了提出的电机DTC控制系统的转速和转矩响应快速,转矩脉动大大减小,系统具有良好的动、静态性能。

直接转矩控制;自杭扰控制器;矩阵变换器;感应电机;PID控制;boost斩波器

0 引 言

直接转矩控制(Direct Torque Control,DTC)克服了以传统磁场定向的矢量控制(Vector Control,VC)中对参数敏感的缺陷,不需要将感应电机(induction motor,IM)输出转矩转换成等效的电流参考值,也不需要复杂的控制器［1-2］。它以转矩为中心,以定子磁场定向的方式实现综合控制,避免了VC的复杂坐标变换与电机模型的数学处理,直接在电机定子坐标上计算磁链和转矩的大小,实现定子磁链和电磁转矩的双闭环控制,能够获得实时快速的控制效果［3-5］。但常规的DTC系统采用PI控制器来实现转速的控制,虽然具有结构简单、控制方法易实现的优点,但不能解决稳定性和快速性之间的矛盾,需要根据不同的控制对象来调节控制器的参数,这给调试过程增加了难度。文献［6］提出的自适应速度观测器有效的改善了系统的动态性能,但其参数自适应律选择困难,无法准确的对电机速度进行辨识;文献［7］将低通滤波器与PLL锁相环相结合进行磁链估计的方法提高了定子磁链的估计精度,使定子电阻具有良好的鲁棒性,但其稳定性受锁相环的输入相位差影响较大;文献［8-9］引入的自抗扰控制器(Active Disturbance Rejection Control,ADRC)不依赖控制对象的数学模型,处理具有非线性和不确定性的控制系统有很好的效果,但常规ADRC的参数多,整定复杂,需要反复试凑,难以达到理想控制效果。

此外,在DTC系统中,一般还需采用电压源逆变器(Voltage Source Inverter,VSI),但相比于VSI,近年发展起来的新兴“绿色”变频器?矩阵变换器(Matrix Converter,MC)具有能量可双向流动、输入电流和输出电压正弦、无需储能原件、任何负载下可实现单位功率因数运行的显著优点［10］,它有逐步取代传统变换器的趋势［11-15］。但常规MC的电压传输比较低［16］,难以满足感应电机的电压要求。

针对上述传统DTC存在的控制器和变换器的两个问题,本文提出了相应的解决办法,即采用简化参数的ADRC控制器和具有升压功能的MC变换器。其中:采用简化参数的ADRC控制器来实现对转矩的实时跟踪,避免普通ADRC繁杂的参数整定过程［17-20］,实现了ADRC参数优化;而采用具有升压功能的MC变换器,可提高电压传输比,从而驱动交流电机的运行。计算机仿真结果验证了本文提出的方法的可行性和有效性。

1 系统总体结构及工作原理

本文提出的DTC控制系统的总体结构如图1所示。图中,两处加粗的方框(即控制器和变换器)为本文创新之处,传统DTC系统中控制器、变换器一般采用PID或常规ADRC控制器、VSI逆变器或常规MC变换器,而本文提出的DTC系统中它们被新型ADRC控制器、新型MC变换器取代。

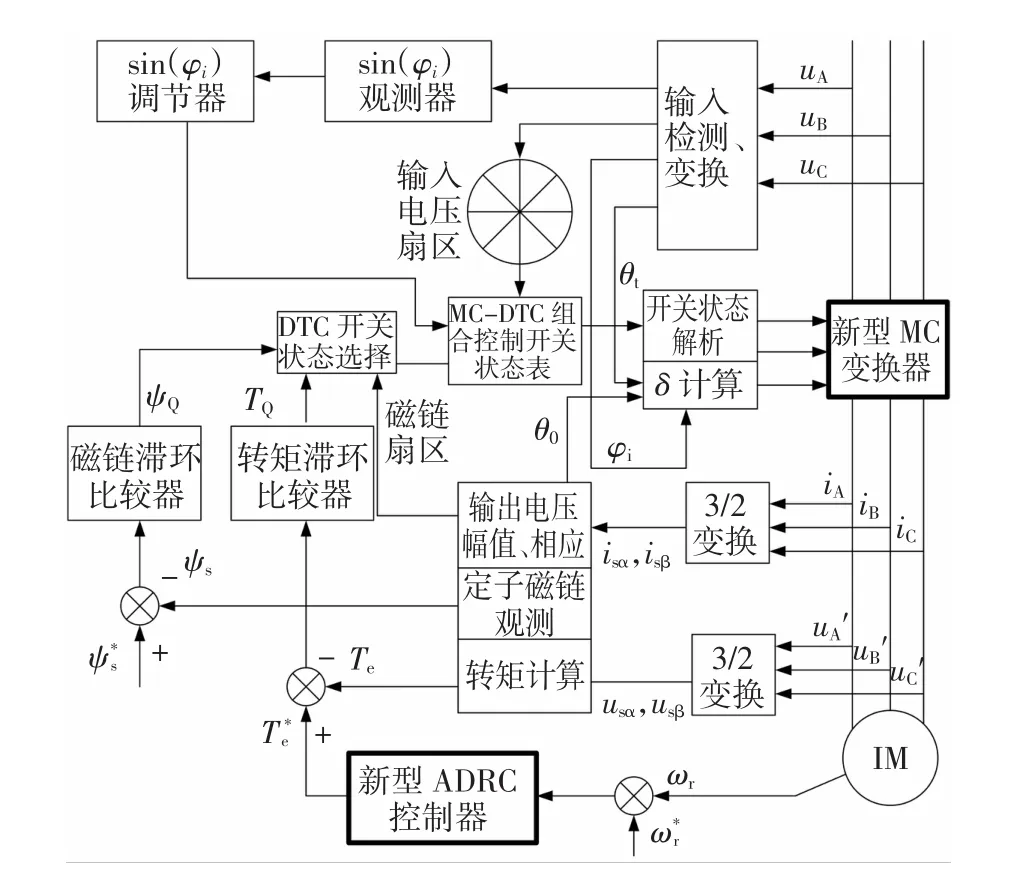
图1 本文DTC控制系统的总体结构Fig.1 Overall structure diagram of DTC control system in this paper

DTC采用了双闭环控制,实现矩阵变换器的空间矢量调制和异步电动机的直接转矩控制。其中:内环由转矩Te滞环比较器、磁链Ψs滞环比较器和功率因数sin(φi)等组成;外环为转速ω控制器。内环、外环分别负责DTC系统参数的粗调控制、精调控制。

图1中转速给定ω*r通过新型ADRC外环控制器进行调节,将实际转速和给定转速转化为电磁转矩的给定值T*e。感应电机的定子电压电流经过3/2变换得到两相静止的电压电流,由此可以得到磁链和转矩的估计值以及磁链的扇区划分。比较转矩Te、磁链Ψs的参考值与估计值,产生的结果输入到相应的滞环比较器中得到控制信号TQ和ΨQ,把定子磁链所在的扇区信息、转矩滞环比较器的输出、输入电压矢量所在扇区信息、功率因数滞环比较器输出送到开关选择表中,以完成开关状态的实时选择,输出电机要求的电压。

由于传统DTC的外环采用的PI控制器的动静态性能及鲁棒性较差,本文外环将采用一种新型ADRC控制器(即简化参数的ADRC控制器)取代PI控制器。

另外,针对常规MC存在电压传输比较低的缺陷,本文将采用一种新型MC(即具有升压功能的MC)取代之,它通过开关状态解析来控制MC的功率开关,从而为电机提供所要求的输入电压。

2 简化参数的新型ADRC

2.1 一般ADRC的原理

ADRC综合了经典调节理论和现代控制理论的优点,能够自动补偿被控对象的内外扰动［17］,克服了经典PID控制器直接取参考值与实际值之间的差值作为控制量的缺陷。理想情况下,ADRC主动从输入输出信号中提取扰动信息,在扰动还未影响输出之前控制量就能将其抵消［18］。

ADRC由跟踪微分器(TD)、扩张状态观测器(ESO)和非线性反馈控制律(NLSEF)三个部分构成。其控制系统结构如图2所示。

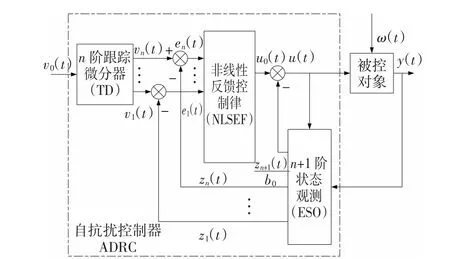
图2 自抗扰控制器系统结构Fig.2 Diagram of ADRC

ADRC系统在输入端加入了非线性跟踪微分器TD,实现对输入信号的快速跟踪,同时输出近似微分信号以及安排过渡过程;ESO是控制器的核心单元,其实时估计被控对象的未知外扰与系统模型之间的误差而加以补偿,不依赖于对象的具体数学模型和外扰的具体形式;再结合NLSEF缓解了快速性和超调之间的矛盾,提高了系统的适应性和鲁棒性。

一般高阶控制对象可近似简化为2阶控制对象,2阶ADRC的各部分形式分别为:

1)跟踪微分器(TD)

对设定输入信号v(t),TD给出它的跟踪信号v1(t)及其微分信号v2(t)。它的动态方程为:

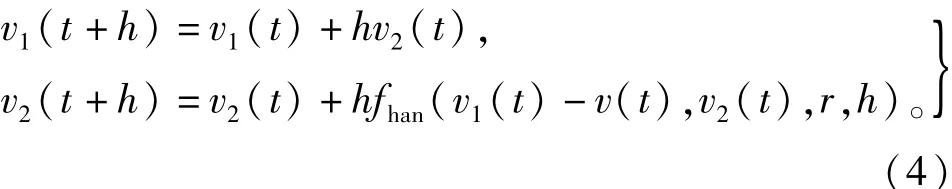
式中:h为采样步长;r决定跟踪过渡过程的速度因子;fhan(.)为时间最优控制综合非线性函数［19］。

2)扩张状态观测器(ESO)

常用的3阶ESO的动态方程为:

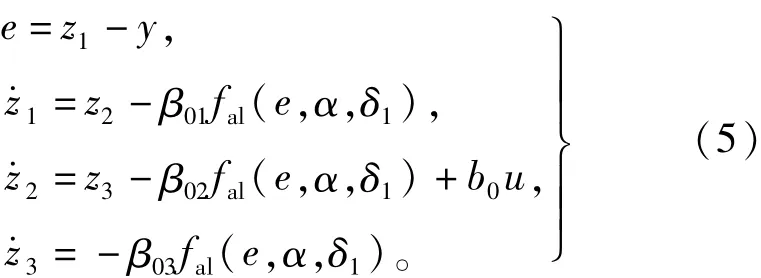
式中:fal(.)为非线性组合函数;z1(t)、z2(t)、z3(t)都为ESO的输出状态估计信号,z1(t)、z2(t)为y(t)、y·(t)的估计变量,z3(t)为总干扰量中未知部分的估计。只要合理选取参数β01、β02、β03,ESO就能给出满意的估计信号。

3)非线性反馈控制律(NLSEF)

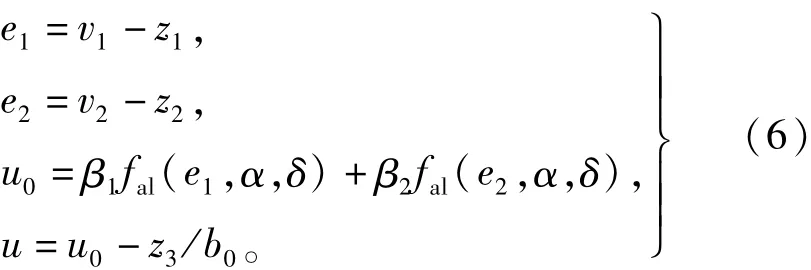
式中:β1、β2分别表示表示比例增益、微分增益;u0的表达式称为非线性状态误差反馈控制律;u中-z3/b0可将未知扰动部分补偿掉。

由此可知,TD需要整定的参数为:r,h;ESO需要整定的参数为:β01,β02,β03,α和δ1;NLSEF需要整定的参数为β1,β2,α和δ;此外,还有fal(.)函数里中控制参数b0需要整定。

2.2 简化参数的ADRC

由于ADRC的参数整定极为繁琐,并且很多参数整定过程没有实际的理论依据,只有凭借操作者的经验积累,这就给控制精确度带来了很大的影响,为此有必要进行模型优化［5］。

设被控对象模型为:

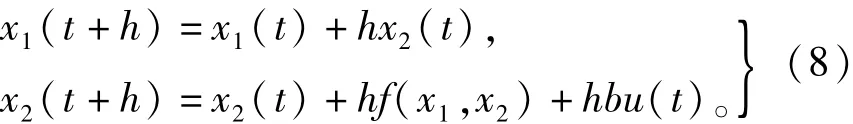
式中f(x1,x2)为含有x1与x2的任意函数。

为便于分析,令图3中TD的参考输入v0(t)= 0,令式(4)中fhan(v1(t)-v(t),v2(t),r,h)=u1(t)。由于TD能对输入信号快速跟踪,故v1(t)≈0,此时,扩张状态观测器ESO可以对被控对象进行准确的观测。f(x1,x2)则由z3(t)完全补偿,被控对象(8)可表示为:

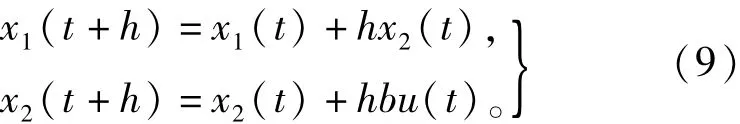
由式(4)～式(9)可得模型误差为:

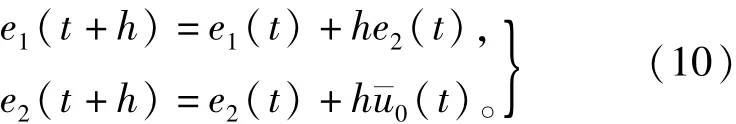
其中:e1(t)=v1(t)-x1(t),e2(t)=v2(t)-x2(t),¯u0(t)=u1(t)-bu(t)。

因此,只要找到合适的¯u0(t)就能误差趋向于0。由式(4)和式(10)结构对比,可令¯u0(t)= fhan(e1,e2,r,h),此时e1(t)和e2(t)可以以最快的速率趋向于0,极大的减少了超调时间。故

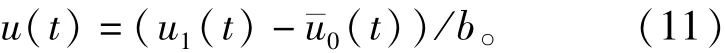
这种方法摒弃了式(6)中将非线性PID作为NLSEF控制函数的传统做法,而是采用了fhan(.)函数,使得各参数具有明确的物理意义。其中满足控制条件的控制量最大值r、采样周期h、控制系数b都不需要整定,从而使得NLSEF单元不会产生额外的未知参数,大大降低了操作复杂性。

3 基于三相boost斩波器的新型MC

MC是一种新型的交-交变换器,其具有正弦输入输出波形、可实现功率的双向流动、输入功率因数可控、不需要直流大电容等优点［1］,已经有取代当前普遍使用的脉宽调制型电压源逆变器(PWMVSI)的趋势,但是常规MC的电压传输比偏低,可能造成电压不足,引起电磁转矩下降,转速也会相应降低,影响电机的正常运行。

针对传统MC的弊端,本文采用一种基于三相boost型交流斩波器的新型MC(Boost Chopper MC,BCMC)［11-12］,并将其应用在感应电机DTC系统中。

1)BCMC的拓扑结构及调制策略

三相boost型交流斩波器的结构如图3所示。此结构选择适当的调制方式可以实现输入输出相位不变,而实现输出幅值的增加［12,14］,但其输入功率因数不可控,可能会给电网带来谐波污;且不能实现输出频率的变化,不利于实现电机的软启动、平滑调速等要求,同时可能产生不必要的额外损耗。

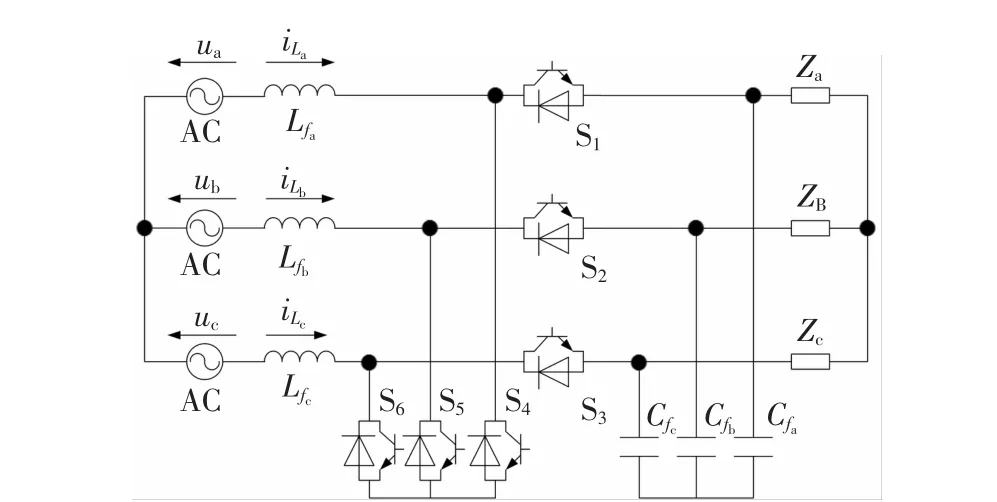
图3 三相boost型交流斩波器Fig.3 Three-phase boost AC/AC chopper

本文考虑将负载侧开关S1,S2和S3取为3×3矩阵变换器,以此形成基于三相boost型交流斩波器的矩阵变换器(BCMC),其拓扑结构如图4所示。

BCMC的控制策略及控制信号形成分别如图5、6所示,在每个开关周期TSeq中,时间间隔ts内,以矩阵形式连接的开关关断,而电源侧的开关SL导通,此时能量储存于电感LS1、LS2与LS3中;时间间隔tL内,以矩阵形式相连的开关按照所选择的调制方式导通或关断,而电源侧的开关SL关断,此时储存在电感中的能量转移给负载,输出电压uA、uB和uC的幅值由所要求的输出频率决定。

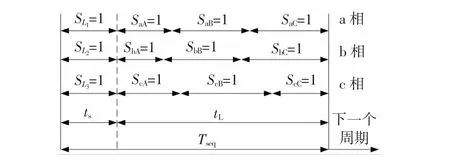
图5 BCMC控制策略示意图Fig.5 Schematic diagram of BCMC control strategy

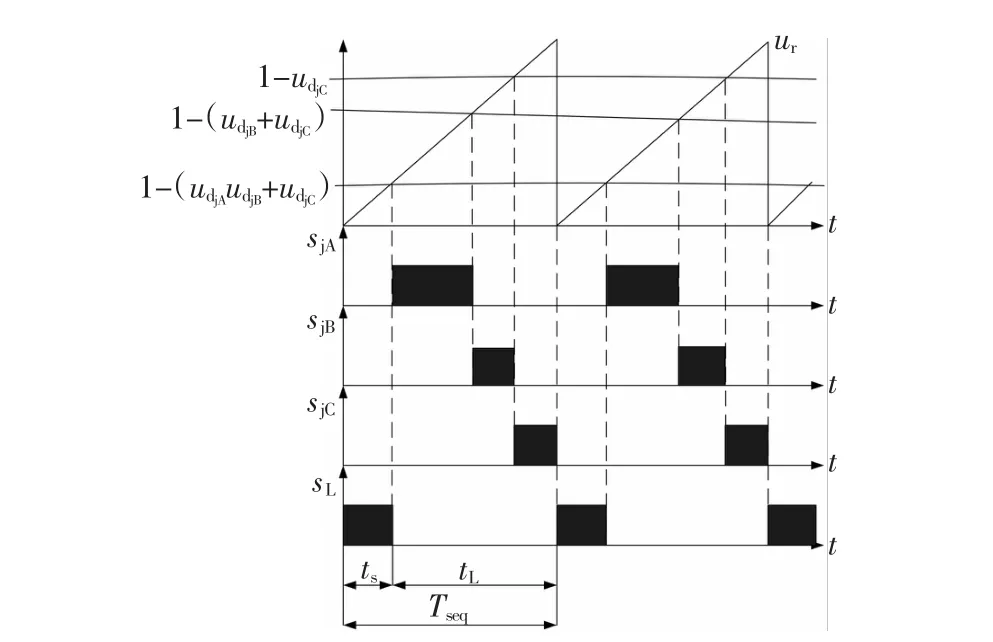
图6 BCMC控制信号波形Fig.6 W aveform of BCMC control signal

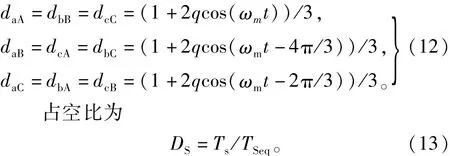
式中:q为控制变量;ωm=ωL-ω,ωL、ω分别为负载、电源要求得到的角频率。

2)BCMC的模型分析

假定BCMC中所有开关都是理想开关,电感和电容呈线性,则BCMC的数学模型可表示为

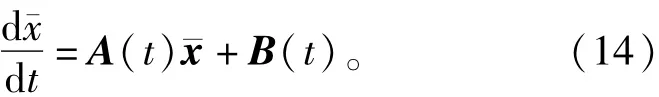
式中:x¯=［¯iS1¯iS2¯iS3u¯L1u¯L2u¯L3］T为平均状态矢量A(t)、B(t)分别为BCMC的参数矩阵、矢量矩阵它们具体可表示为: ;。

为了获得稳定的状态空间模型,引入3/2变换阵:

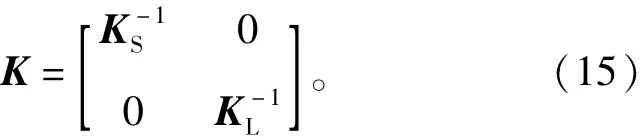
其中,

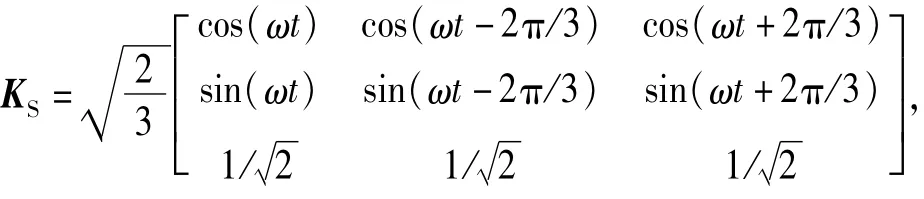
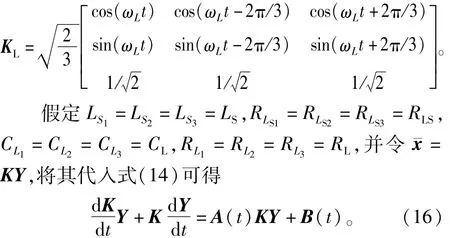
通过矩阵求逆和变形,可得BCMC在αβ两相静止坐标下的数学模型为:

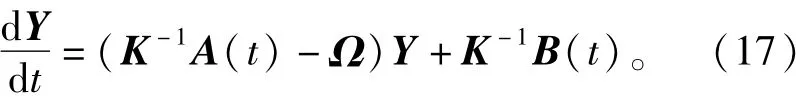
其中,

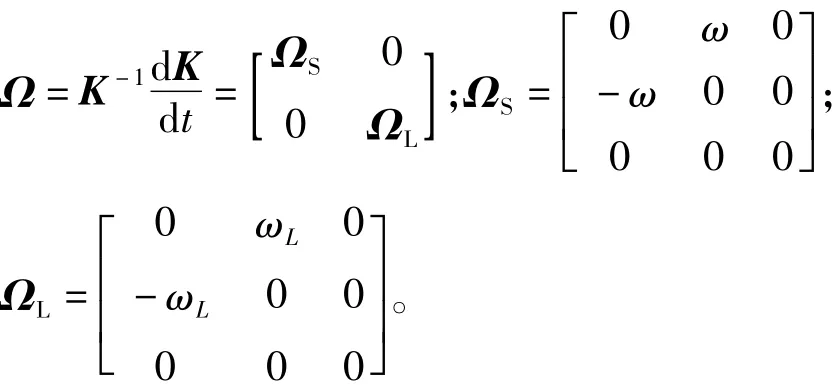
定义BCMC新的参数矩阵和矢量矩阵:K-1A (t)K=A;K-1B(t)=B。由此可以得到BCMC稳定的状态空间模型为

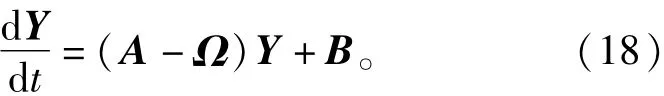
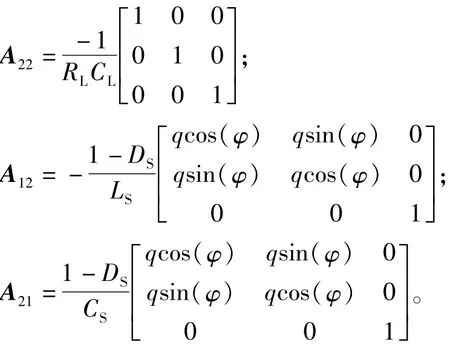
由式(18)可以解得

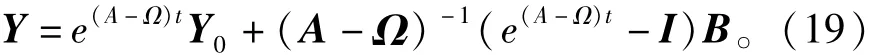
式中:I为单位矩阵;Y0为状态变量的初始值。

将式(19)代入¯x=KY,可得BCMC的状态变量在abc静止坐标系下可以描述为

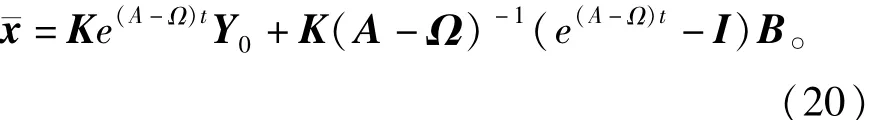
所以其稳态值为

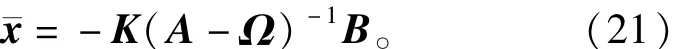
解得A相的负载电压、电源电流分别为

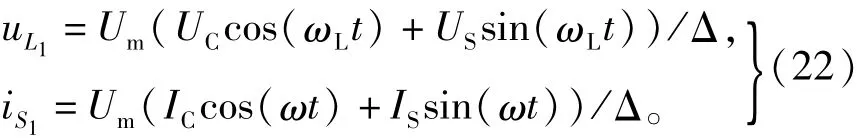
其中,

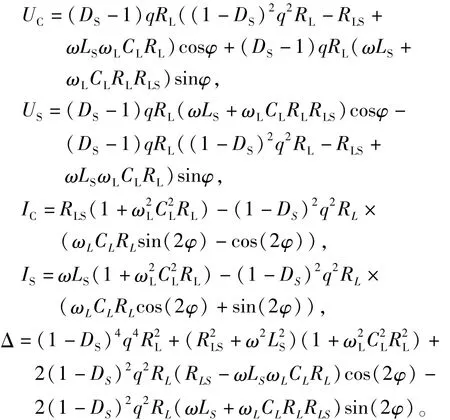
B相、C相的负载电压、电源电流与A相类似,略去。

4 仿真分析

下面在Matlab/SIMULINK平台下进行仿真验证。仿真中,异步电机参数取为:Pe=1.7 kW,Ue= 220 V,Rs=0.487Ω,Ls=0.285 H,Lr=0.25 H,Lm= 0.124H,j=0.087 kg·m2,np=2;MC参数取为:Ls1= Ls2=Ls3=0.5mH,CF1=CF2=CF3=50μF;ADRC参数取为:h=1e-3,r=1.5e+5,δ1=0.01,β01= 1e+3,β02=1.5e+4,α=0.5。

5.1 正常情况下的对比分析

1)本文提出的基于BCMC-ADRC的DTC系统与传统的基于VSI-PI的DTC系统仿真比较。

仿真中,PI调节器参数取为:kp=0.18,ki= 0.05;MC输入相电压有效值为220 V,初始转矩为0,在0.5 s时上升为15 N·m,在0.9 s时回到0值;转速在0.35 s时由初始值500 rad/s下降为200 rad/s。

图7、图8、图9、图10分别为转速、转矩、基于BCMC-ADRC的DTC系统的定子磁链、基于VSIPI的DTC系统的定子磁链波形。

由图7、图8可见,ADRC系统较PI系统而言,转速能更快更准确的达到给定值,且超调量较小;转矩响应速度更快,且转矩脉动大大减小,稳态误差更小。

由图9、图10可见,ADRC控制系统定子磁链的抖动更小,轨迹更加圆滑。

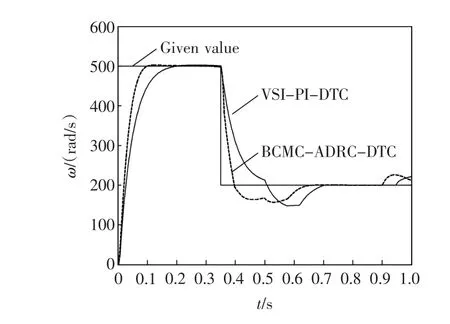
图7 转速响应波形Fig.7 Waveform of speed response

图8 转矩响应波形Fig.8 Waveform of torque response

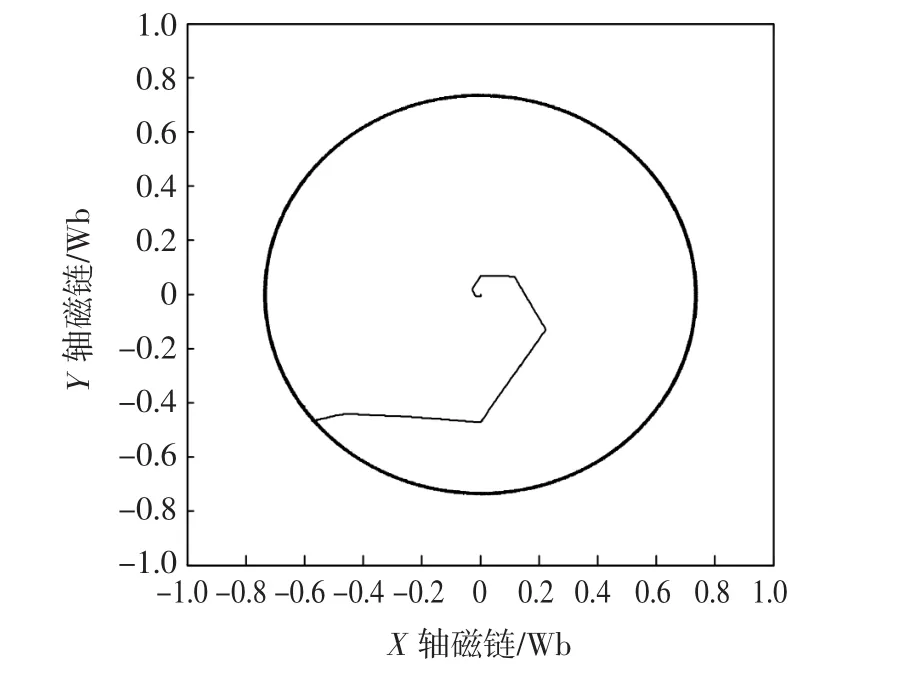
图9 ADRC控制系统定子磁链轨迹Fig.9 Stator flux trajectory of ADRC control system

2)本文提出的基于BCMC-ADRC的DTC系统与基于传统MC-ADRC的DTC系统仿真比较。

图11、图12、图13、图14分别为BCMC输出电压电流、MC输出电压电流、转速、转矩。

由图11、图12可见,BCMC相比于MC,其电压传输比有明显提高,可以方便的为电机提供所需的额定电压。

由图13、图14可见,在电机要求的转速较高时,利用BCMC可使转速迅速达到给定值,而传统MC达不到要求;BCMC的系统转矩也能迅速达到给定转矩且转矩脉动较小,而传统MC跟踪速度明显偏慢,且转矩脉动也较大。

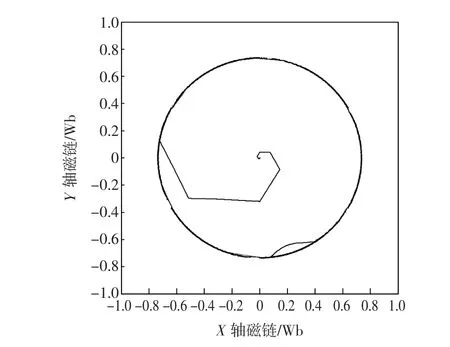
图10 PI控制系统定子磁链轨迹Fig.10 Stator flux trajectory of PI control system

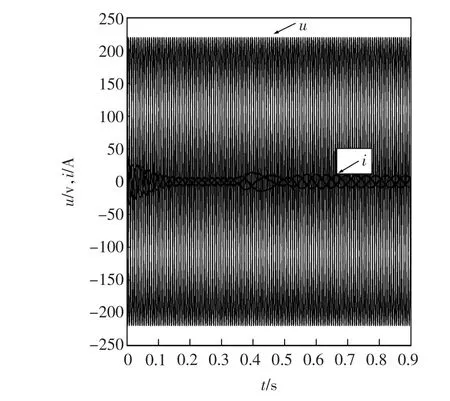
图11 BCMC输出电压电流波形Fig.11 Output voltage and current waveform of BCMC

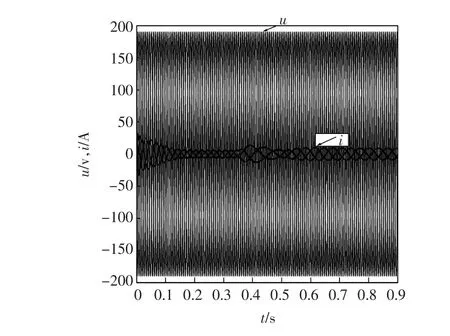
图12 MC输出电压电流波形Fig.12 Output voltage and current waveform of MC

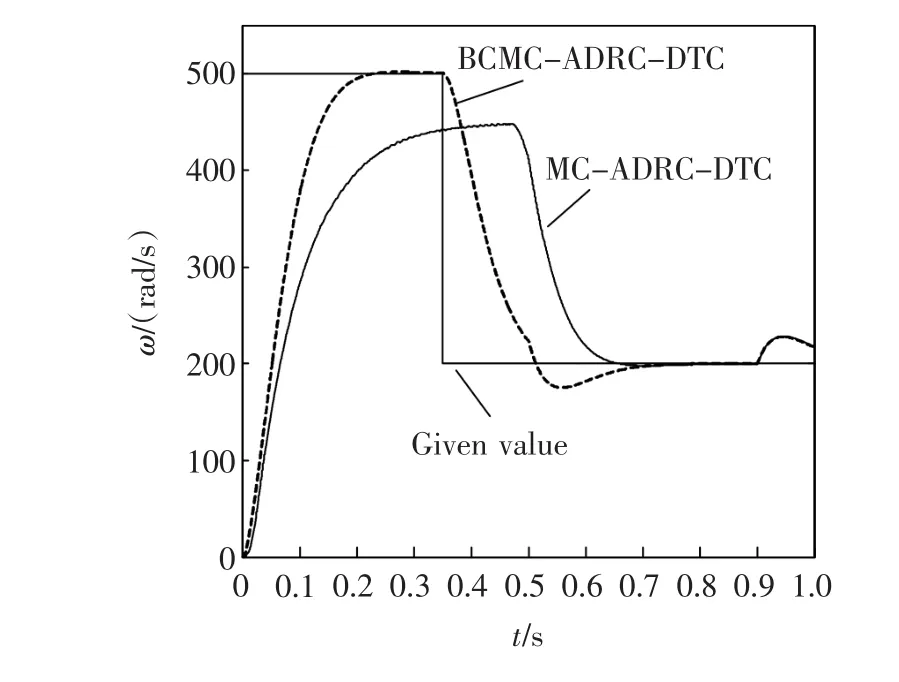
图13 转速响应波形Fig.13 W aveform of speed response

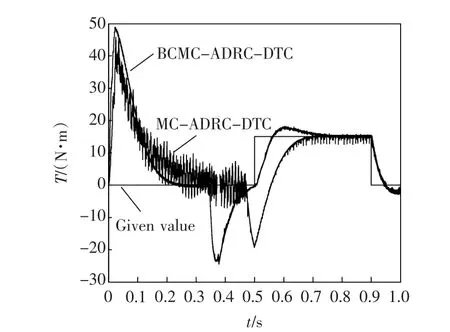
图14 转矩响应波形Fig 14 Waveform of torque response

5.2 干扰情况下的对比分析

基于BCMC-ADRC的DTC系统与传统VSIPI的DTC系统分别在两种干扰情况下进行仿真比较。

1)转矩变化干扰

设置电机在空载情况下起动,在0.5 s时突加转矩为15 N·m,之后维持不变,给定转速为500 rad/s。

图15为这种情况下的两种DTC系统的转速波形。由图可见,当转矩变化时,传统基于VSI-PI的DTC系统转速恢复时间大大延长。

2)转动惯量、摩擦系数的变化干扰

设置电机在0.5 s时转动惯量突然从0.087 kg·m2改变为0.097 kg·m2或摩擦系数突然从0.2 N·m·s改变为0.5 N·m·s。

图16、图17分别给出了增大转动惯量和改变摩擦系数时转速响应的变化情况。

由图16、图17可见,两种干扰情况下基于BCMC-ADRC的DTC系统转速响应基本没有变化,而传统基于VSI-PI的DTC系统的转速上升时间由原来的0.2 s分别上升为0.25 s和0.28 s。

通过上面仿真可证明,本文提出的基于BCMCADRC的DTC系统具有更好的抗干扰能力,鲁棒性更强。

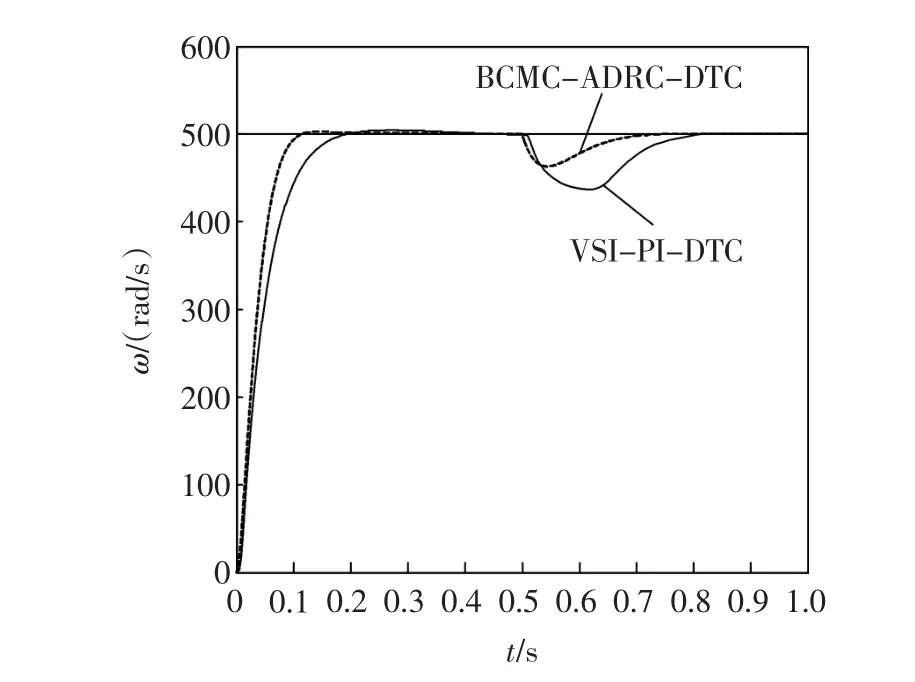
图15 转矩变化时转速响应波形Fig.15 Waveform of speed response under torque changing

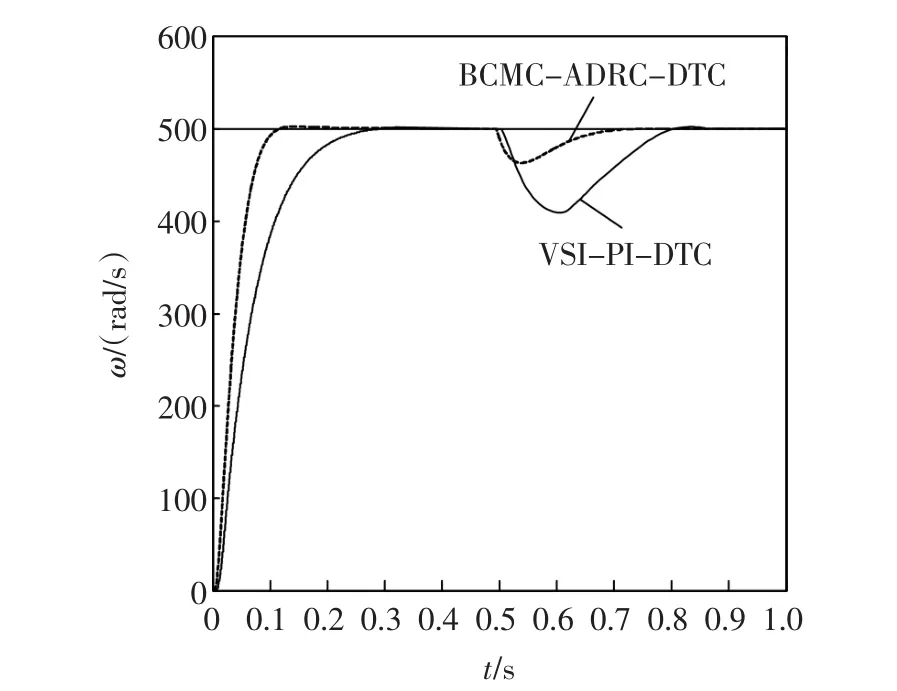
图16 增大转动惯量时转速响应曲线Fig.16 Waveform of speed response under inertia increasing

图17 改变摩擦系数时转速响应曲线Fig.17 Waveform of speed response under friction factor changing

通过上面大量仿真可见,本文提出的基于BCMC-ADRC的DTC系统控制性能指标优于基于VSI-PI或基于传统MC-ADRC的DTC系统。

6 结 论

本文构造了一种基于简化参数ADRC的MCDTC系统,并且针对MC-DTC系统中MC的电压传输比较低的弊端,提出采用BCMC新型矩阵变换器。仿真结果表明本文所提出的基于BCMC-ADRC的DTC系统具有良好的性能,主要表现在:

1)相比基于传统VSI-PI的DTC系统,本文提出的系统反应更快、更准确,且超调量较小、转矩脉动更小;

2)相比基于传统MC的DTC系统,本文提出的系统克服了电机输入电压不足而可能引起的转速偏低的缺陷,保证电机的正常运行;

3)本文提出的系统具有更好的抗干扰能力。

［1］ 王晶鑫,姜建国.基于磁场定向的矩阵变换器驱动感应电机变结构直接转矩控制［J］.中国电机工程学报,2010,30(6):57 -62. WANG Jingxin,Jiang Jianguo.Variable-structure direct torque control for induction motor driven by a matrix converter based on field oriented［J］.Proceedings of the CSEE,2010,30(6):57-62.

［2］ TOBIASGeyer,SENIOR Member.Model predictive direct torque control:derivation and analysis of the state-feedback control law［J］.IEEE Transactions on Industry Applications,2013,49(5): 2146-2157.

［3］ 张麒.三相异步电动机定子磁链观测方法研究［D］.大连:大连交通大学,2010:4-21.

［4］ HOSSEIN Saberi,Mehran Sabahi,et al.Improved sensorless direct torque controlmethod using adaptive flux observer［J］.IEEE on Power Electronics,2014,7(7):1675-1684.

［5］ 卢达.永磁同步电机调速系统控制策略研究［D］.浙江:浙江大学,2013:15-28.

［6］ SATISH,Mohapatra,Mohan.Dynamic performance of a matrixconverter fed speed sensorless DTC induction motor drive using adaptive speed observer［J］.IEEE Applied Power Electronics Conference and Exposition(APEC),2009:1984-1990.

［7］ 何志明,廖勇,李辉.一种新颖的无传感器异步电动机直接转矩控制系统［J］.电工技术学报,2009,24(11):21-25. HE Zhiming,Liao Yong,Li Hui.A novel sensorless induction motor DTC system［J］.Transactions of China Electrotechnical Society,2009,24(11):21-25.

［8］ 潘月斗,徐杰,陈虎,等.ESO在直接转矩控制矩阵变换器中的应用及稳定性分析［J］.控制与决策,2013,28(4):585-589. PAN Yuedou,Xu Jie,CHEN Hu,etal.Stability analysis and application of ESO in direct torque control ofmatrix converter［J］.Control and Decision,2009,24(11):21-25.

［9］ 刘英培.基于自抗扰控制PMSM电压空间矢量调制直接转矩控制方法［J］.电力自动化设备,2011,31(11):78-82. LIU yingpei.Space vector modulated direct torque control for PMSM based on ADRC［J］.Electric Power Automation Equipment,2011,31(11):78-82.

［10］ 邓文浪,崔贵平,袁婷,等.基于双级矩阵变换器的直驱永磁同步风力发电系统有功功率平滑优化控制［J］.电网技术,2013,37(12):3419-3424. DENGWenlang,Cui Guiping,Yuan Ting,et al.Active power smoothing optimization control of direct-driven permanentmagnet synchronous wind power generation system based on two-stage matrix converter［J］.Power System Technology,2013,37(12): 3419-3424.

［11］ 宋卫章,钟彦儒,孙向东.具有高电压传输比且能抵御非正常输入的Z—源双级矩阵变换器［J］.中国电机工程学报,2010,30(24):21-28. SONGWeizhang,Zhong Yanru,Sun Xiangdong.Z-source twostagematrix converterwith high voltage transfer ratio and immune to abnormal input voltages［J］.Proceedings of the CSEE,2010,30(24):21-28.

［12］ 张友军,阮新波.相位和幅值可控电压调节器［J］.中国电机工程学报,2010,30(36):86-92. ZHANG Youjun,Ruan Xinbo.Voltage regulatorwith controllable phase and amplitude［J］.Proceedings of the CSEE,2010,30 (36):86-92.

［13］ 徐志强,李娜,刘彪,等.矩阵变换器双电压合成控制策略［J］.电网技术,2008,32(13):45-49. XU Zhiqiang,Li Na,Liu Biao,et al.Analysis on anti-power system disturbance performance of dual line to line voltage synthetic control strategy for matrix converter［J］.Power System Technology,2008,32(13):45-49.

［14］ 张友军,丁明昌,任永保,等.级联式Buck-Boost AC/AC变换器［J］.电力自动化设备,2010,30(9):46-50. ZHANG Youjun,Ding Mingchang,Ren Jibao,et al.Cascaded buck-boost AC/AC converter［J］.Electric Power Automation E-quipment,2010,30(9):46-50.

［15］ 丁明昌.π型AC/AC交流变换器及其变结构控制策略的研究［D］.苏州:苏州大学,2011.

［16］ 李生民,李杨,钟彦儒,等.抑制电网异常的高电压传输比矩阵变换器［J］.电网技术,2010,34(10):115-120. LIShengmin,Li Yang,Zhong Yanru,et al.High voltage transfer ratiomatrix converter capable of enduring abnormal conditions in power grid［J］.电网技术,2010,34(10):115-120.

［17］ 刘星桥,胡建群,周丽.自抗扰控制器在三电机同步系统中的应用［J］.中国电机工程学报,2010,30(12):80-85. LIU Xingqiao,Hu Jianqun,Zhou Li.Active disturbance rejection control of three-motor synchronouscontrol system［J］.Proceedings of the CSEE,2010,30(12):80-85.

［18］ 高志强.自抗扰控制思想探究［J］.控制理论与应用,2013,30(12):1498-1510. GAO Zhiqiang.On the foundation of active disturbance rejection control［J］.Control Theory&Applications,2013,30(12): 1498-1510.

［19］ 孙彪,孙秀霞.离散系统最速控制综合函数［J］.控制与决策,2010,25(3):473-477. SUN Biao,Sun Xiuxia.Optimal control synthesis function of discrete-time system［J］.Control and Decision,2010,25(3):473 -477.

［20］ REN Yifeng,DUAN Xiaoli.Research of Active Disturbance Rejection Controller in Speed Regulation of Induction Motor［C］// Second International Conference on Mechanic Automation and Control Engineering(MACE),July 15-17,2011,Inner Mongolia,China,2011:7564-7567.

(编辑:贾志超)

Research on control system of DTC for motor based on novel ADRC controller and MC converter

CHENG Qi-ming1, HUANGWei1, CHENG Yin-man2,GUO Kai1, XU Cong1, DENG Liang1
(1.College of Automation Engineering,Shanghai University of Electric Power,Shanghai200090,China; 2.North power supply branch,Shanghai Electric Power Company,Shanghai200041,China)

Because the traditional PID controller parameters robustness and immunity has some defect,direct torque control(DTC)method for inductionmotor(IM)based on active disturbance rejection control (ADRC)of simplified parameterwere proposed.The ADRC speed controller were designed with the given speed and actual speed as the input signal and the given electromagnetic torque as the output signal. In addition,matrix converter(MC)voltage transmission is relatively low in the traditional DTC system,it is difficult tomeet the voltage requirements for themotor,so itaffects the output characteristics of themotor directly.A novelmatrix converter combined the advantages of three-phase boost chopper and matrix converter were proposed and themodel analysis prove the rationality of the topology.The simulation results effectively prove that the torque and speed of the motor respond quickly,the torque ripple are reduced greatly,and the system has good dynamic and static performance.

direct torque control(DTC);active disturbance rejection control(ADRC);matrix converter (MC);induction motor(IM);PID Control; boost chopper

10.15938/j.emc.2015.08.009

TM 762;TM 343

A

1007-449X(2015)08-0053-09

2014-12-03

国家自然科学基金(61304134);上海市重点科技攻关计划(14110500700);上海市电站自动化技术重点实验室(13DZ2273800);上海市自然科学基金(13ZR1417800)

程启明(1965—),男,博士,教授,硕士生导师,研究方向为电力系统自动化、发电过程控制等;黄 伟(1989—),男,硕士研究生,研究方向为电力系统自动化、电机控制等;程尹曼(1990—),女,本科,研究方向为电力系统自动化、新能源发电控制等;郭 凯(1989—),男,硕士研究生,研究方向为电力系统自动化、电机控制等;徐 聪(1990—),男,硕士研究生,研究方向为电力系统自动化、电机控制等;邓 亮(1981—),男,博士,硕士生导师,研究方向为新能源控制、非线性系统、精密制造系统的智能控制等。

程启明