微分学基本定理评注

张明会 高婷婷

（陇南师范高等专科学校数信学院，甘肃成县 742500）

微分学基本定理评注

张明会 高婷婷

（陇南师范高等专科学校数信学院，甘肃成县 742500）

微分学主要处理的是连续函数的变化率问题，它的基本定理、概念、原理和方法是高等数学的主干，也是高等数学尤其是数学分析的灵魂．文章从微分学基本理论出发，逐步分析并阐明了微分中值定理间内在联系，以及它们的特征和意义．

微分学；中值定理；评注

微分学的基本定理，又叫微分中值定理，主要指罗尔（Rolle）中值定理、拉格朗日（Lagrange）中值定理、柯西中值定理及泰勒（Taylor）展开定理．这些定理是利用导函数研究函数在区间上的整体性质的重要工具，是微分学通向应用之路的桥梁，他们和实数R的基本性质一起构成了微分学的理论基础．下面我们将着重阐明微分中值定理之间的内在联系，以及它们的特征和意义．

1 微分中值定理结构框

图1 微分中值定理结构图

图1中纵向中间的三个定理，是微分中值定理的主干定理，箭头表明三个中值定理公式之间是“特殊”与“一般”的关系，即下面是上面的特例，上面是下面的推广．

2 建立与证明微分中值定理的思路分析

微分中值定理的建立以及它们的分析证明思路的形成，有着深刻的几何背景，与实数R的基本定理相比，这似乎是它们的突出特征．认真体会这些定理建立过程中的几何直观因素，对于培养把抽象的分析论证与形象的几何直观模型相互借用的能力，有重要的意义．

罗尔定理是微分中值定理中最简单的情形，其几何意义是：在区间[a，b]上两端等高的一条连续曲线y=f（x），若在（a，b）内的曲线上处处有切线，那么其中必有一条切线与x轴平行．

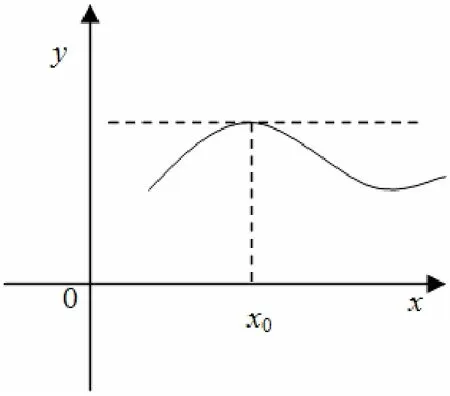
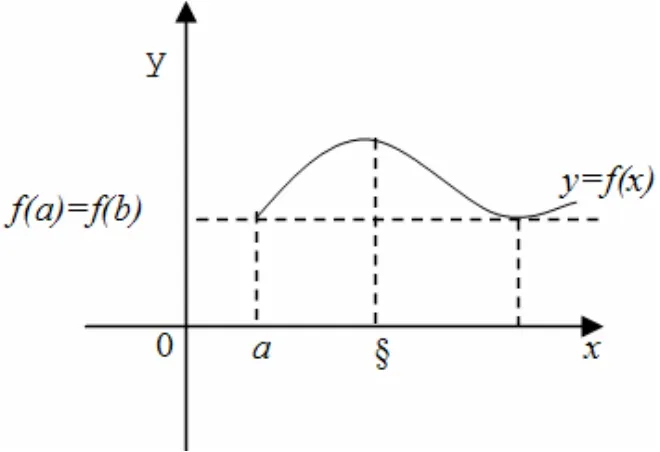
从图形上发现，y=f（x）如果存在极值f（x0），那么曲线在极值点上的切线平行于x轴，即f’（x）=0．闭区间上连续函数的性质保证函数必有最大值和最小值，即保证了极值点的存在．同时，由条件f（a）=f（b）又限制函数的最大值和最小值一般不可能在区间端点a，b上出现，因此，必然存在一点ξ∈（a，b），使函数在其上达到极值，即f’（ξ）=0．这就是建立罗尔中值定理的基本几何事实．借助几何直觉从而给出了抽象的分析证明．

拉格朗日中值定理是罗尔中值定理的推广，当拉格朗日中值公式f’（ξ）=（f（b）－ f（a））/（b－ a）中f（a）=f（b）时，就成了罗尔定理．因此，拉格朗日中值定理仍然具有鲜明的几何意义，当f（a）≠f（b）时，如图所示：

公式中（f（b）－ f（a））/（b － a）是联结二端点（a，f（a）），（b，f（b））的弦的斜率，拉格朗日中值定理肯定在（a，b）内存在点ξ，使得曲线上过（ξ，f（ξ））端点切线与这条弦平行，弦的方程：

y=（（f（b）-f（a））/（b-a））×（x-a）-f（a）

它与函数曲线y=f（x）的纵坐标的差是：

h（x）=f（x）－（（f（b）－ f（a））/（b－ a））×（x－ a）+ f（a）

由图可以看出，h（x）满足罗尔定理的所有条件，因此，在拉格朗日中值定理的证明中，首先构造辅助函数h（x），然后验证它满足罗尔定理的条件，使定理得证．构造辅助函数证明有关问题，是数学分析中常见的方法，而辅助函数的构造方法，往往是从一些几何事实的直觉中得到启示的．

柯西中值定理的证明也是如此，若令x=f（t），y=f（t），那么就是平面上以（g（a），f（a）），（g（b），f（b））为端点的一段曲线，连接这两点的弦的斜率是：

（（f（b）－ f（a））/（（g（b）－ g（a））

曲线在（g（t），f（t））处的切线斜率是：dy/dx=f’（t）/g’（t），

定理肯定存在ξ∈（a，b），使得曲线在点（g（ξ），f（ξ））的切线和连接两端点（g（a），f（a）），（g（b），f（b））的弦平行．

同样，曲线方程的纵坐标y=f（x）与弦方程的纵坐标y=（（f（b）－ f（a））/（g（b）－ g（a）））×（g（t）－ g（a））+f（a）之差h（t）=f（t）－（（f（b）－ f（a））/（g（b）－ g（a）））×（g（t）－ g（a））－ f（a）满足罗尔定理的条件，因而就以h（t）作为辅助函数，使定理得证．

3 几点评注

（1）罗尔定理是拉格朗日中值定理的特例，柯西中值定理又是拉格朗日中值定理的推广，其中拉格朗日中值定理是核心，拉格朗日中值定理是用函数的局部性质研究函数整体性质的桥梁，其应用十分广泛．

（2）微分中值定理的证明是建立在闭区间上连续函数的整体性质之上的，因此它们与数系的性质有关，如果除掉数系的完备性，微分中值定理将不成立．例如，对定义在闭区间[0，1]上的有理数集上的连续函数f（x）= x-x3，罗尔定理就不成立．

（3）函数f（x）在点x0的泰勒公式为：

其余项Rn（x）有三种形式：

二者有本质差异，拉格朗日余项和柯西余项是定量形式，便于定量分析和误差估计，其泰勒公式反映了区间上的整体性质；皮亚诺余项是定性形式，便于考察函数的变化状态，在确定极限时有用，其泰勒公式只能反映函数在某点邻域的局部性质．泰勒公式的重要意义是，它表明在x0点具有n+1阶导数的函数f（x）可以用n次多项式作局部逼近，在级数理论、函数逼近和解析函数研究中有重要应用．

[1]华东师范大学数学系.数学分析[M].北京：高等教育出版社，2001.

[2]马振华.离散数学导引[M].北京：清华大学出版社，2006.

[3]裴礼文.数学分析中的典型问题与方法[M].北京：高等教育出版社，2002.

[4]马振民，吕克璞.微积分习题类型分析[M].兰州：兰州大学出版社，1999.

[5]张明会，高婷婷.恒等变换方法在数学分析中的应用[J].湖南工程学院学报，2011（2）.

（责任编辑：于开红）

Commentary on Fundamental Theorem of Differential Calculus

ZHANG Minghui GAO Tingting
(School of Mathematics and Information, Longnan Normal College, Longnan Gansu 742500)

Differential calculus mainly deals with the change rate of continuous function, concept, principle and method, and is the backbone of higher mathematics and the soul of higher mathematics analysis. This paper, from the basic theory of differential calculus, has a step-by-step analysis and clarification of the relationship among differential mean value theorems, and their characteristic and the significance.

differential calculus; differential mean value theorem; commentary

G812.78

A

1009-8135（2015）03-0017-03

2015-02-25

张明会（1981-），男，甘肃康县人，陇南师范高等专科学校数学系讲师，主要研究基础数学．高婷婷（1979-），女，甘肃礼县人，陇南师范高等专科学校数学系讲师，主要研究基础数学．

陇南师范高等专科学校科研项目（2014LSZK02001）、陇南师范高等专科学校教学改革项目（JXGG2013003）阶段性成果