轨道交通直线感应电动机牵引系统精确瞬时速度检测技术研究

刘可安 田红旗 刘 勇

(1.中南大学交通运输工程学院 长沙 410075 2.南车株洲电力机车研究所 株洲 412001)

0 引言

采用直线感应电动机驱动的中低速磁浮和轮轨列车作为新型的城市轨道交通运输工具，具有安全可靠、工程造价低、爬坡能力强、拐弯半径小、噪声低以及最大牵引力发挥不受轮轨粘着关系限制等优点，成为城市轨道交通车辆发展的新方向，在日本、加拿大以及北京、广州等国家和地区10 多条线路成功实现商业运营［1-4］。

直线电动机牵引系统为实现高精度闭环控制需进行速度的实时检测。磁浮列车，大都基于计数轨枕测速法，采用涡流传感器来检测金属轨枕获取速度脉冲［5］，轨枕安装间距多为1.2 m;轮轨列车，在其轮对上安装编码器以实时得到次级速度信息，由于车辆运行中的机械振动使其承受很大的机械应力，故障率相对较高，因此编码器齿数很少。对涡流传感器或编码器输出脉冲的后续处理一般采用M 法、T 法或M/T法以得到速度信息［6］。当列车运行速度较低时，传感器两输出脉冲之间的间隔时间很长，在此间隔内无法获取准确的速度信息，影响系统的低速控制性能［7］。

为实现全速度范围内直线电动机的有效闭环控制，需提高低速工况下的速度检测准确度，针对此问题，国内外学者进行了深入研究，经总结可分为两大类:一是基于电动机数学模型的速度观测方法［8，9］，采用状态观测器对电流、磁链等电动机量进行观测，基于波波夫稳定判据得到速度辨识算法，此类方法能较好地工作在中、高速，但由于其对电动机模型的准确性要求很高，仍未解决低速工况下的速度辨识问题，因此实际工程应用中直线电动机控制仍采用带传感器控制方式;二是基于机械传递函数的瞬时速度观测方法［10-15］，通过全阶或降阶扰动观测器来实现速度观测，结构简单且便于处理器实施。根据文献［10-15］可知，瞬时速度观测方法多应用于开关频率较高的小功率伺服系统，其准确性主要由电动机输出力矩Te、负载转矩TL以及系统的转动惯量Jm决定。当其应用于轨道交通时(应用特点为:系统开关频率小于500 Hz，列车站与站运行过程中，负载、转动惯量恒定且可通过理论计算或辨识得到)，电动机输出转矩Te的准确性直接决定速度观测的精确性，但文献［10-15］均未对低开关频率以及低速工况下力矩Te输出的准确性进行分析，认为其无误差。归纳起来影响低速工况下力矩输出精确性的因素主要有两个:

1)逆变器非线性误差的影响。由于器件死区时间、开通/关断延时以及导通压降等因素，逆变器实际输出电压和理论输出电压之间存在一定误差，在极低速工况下其对控制性能的影响尤为明显，造成电动机输出力矩偏差［16-19］。文献［20-23］对逆变器非线性误差进行了分析和补偿，但均未得到一个总的电压误差，未将导通压降、关断延时分离出来，因此其只适合于计算周期与开关周期相同的高开关频率应用场合。

2)电动机参数误差的影响。地铁工作环境恶劣，电动机初、次级绕组阻值随环境温度以及运行工况等因素而变化，需要进行阻值的实时检测［24］。工程应用中多采用温度传感器(Pt100)进行初级绕组温度的测定，因此需进行次级绕组的在线辨识，文献［25-29］对基于观测器理论的辨识算法进行了研究，但在实际应用中存在如文献［30］所述的收敛性问题，在不同工况下需对其参数进行特殊的配置和工作量极大的试凑调整。

本文提出一种基于牛顿运动模型的直线电动机速度观测算法。为提高速度观测的精确性，提出了一种适合于低开关频率应用场合的逆变器非线性误差补偿算法，并基于电动机本体方程推导了一种能保证稳定性的次级电阻在线辨识算法。基于某地铁项目自主研发的直线电动机牵引控制系统进行了相关算法的实验验证，实验结果表明了所提算法的正确性和有效性。

1 基于牛顿运动模型速度观测器

在控制周期T 内，电动机输出推力Te和负载转矩TL可认为恒定，其加速度a 可认为恒定，电动机在一个控制周期内转过的角度增量Δθ 为

根据牛顿运动方程有

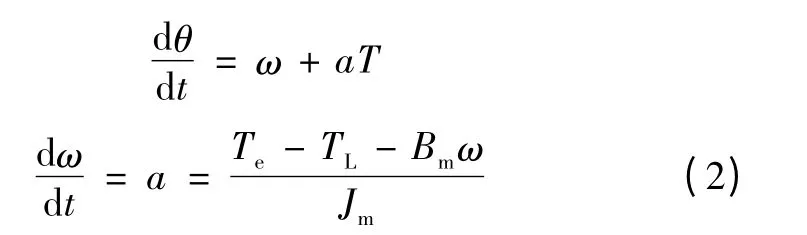
式中:Te为电动机输出推力;TL为负载转矩;Bm为摩擦系数;Jm为转动惯量。在速度较低情况下Bm可近似为0，因此得到

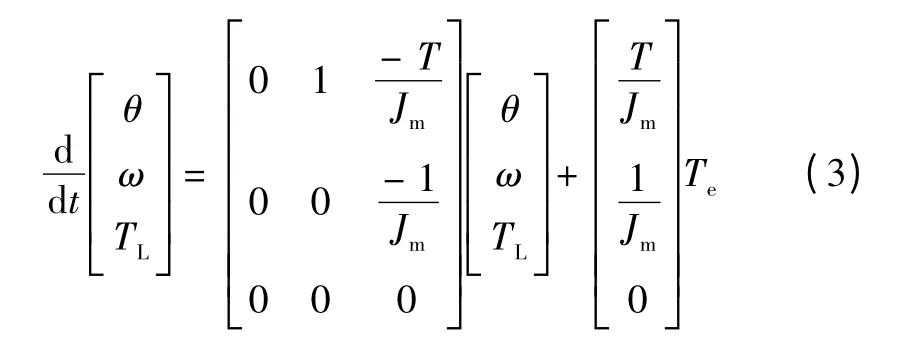
构造状态观测器方程为

则有

其特征方程为

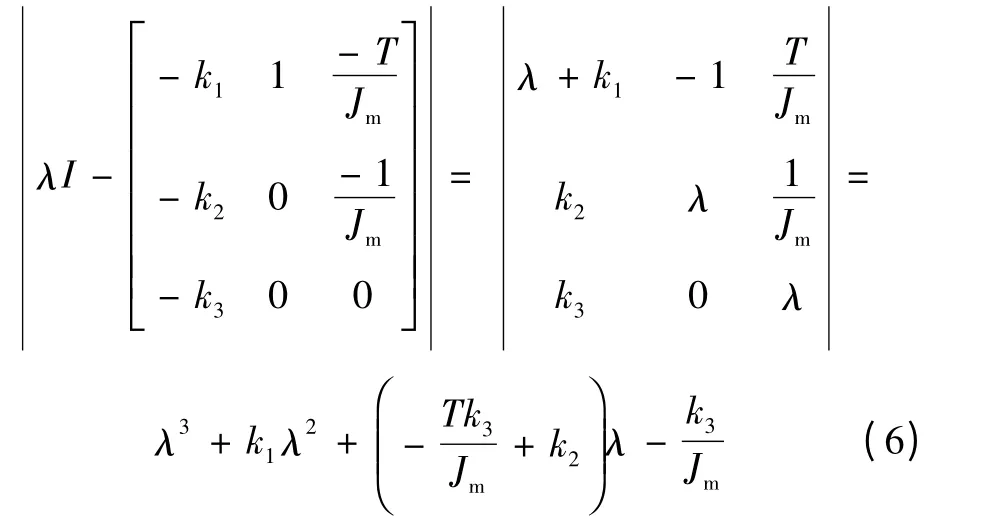
根据要求的极点分布可求出k1、k2、k3值，得到离散观测器方程为

因此可通过式(7)进行瞬时速度观测。

系统控制周期T 一般固定(如100 μs)，涡流传感器或编码器脉冲输出时刻随机，与系统控制周期并非时刻保持一致，存在误差Terror(时序如图1所示)，尤其是在低速工况下，Terror最大接近T。传统的处理方法是直接将tk时刻的角度θk作为t3时刻的角度值，存在失步误差，尤其是在加速度较大的情况下。

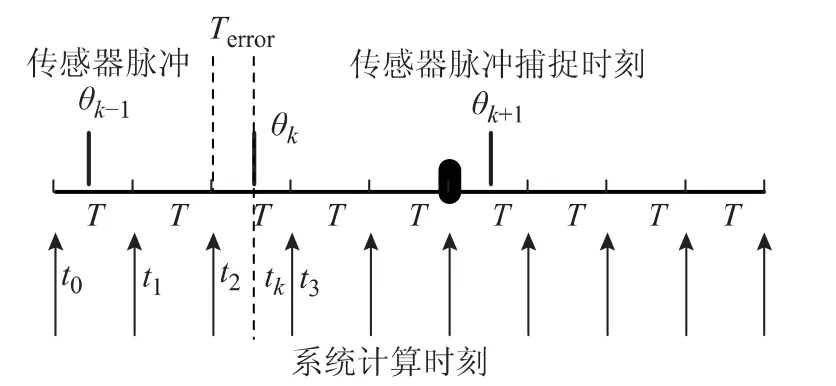
图1 传感器输出脉冲及系统时序图Fig.1 Timing charts for sensor output pulse and system

为解决此问题，在硬件设计上采用FPGA 进行传感器输出脉冲上升或下降沿的精确捕捉，并可精确得到Terror值，对tk时刻的角度和速度进行观测

2 逆变器非线性误差分析及补偿

两电平三相电压型逆变器基本结构如图2所示，电动机用R-L 进行替代以方便进行后续分析，电动机三相连接线缆的电阻用RL表示。逆变器理论及实际输出脉冲分别如图3中虚线及实线所示，导致逆变器理论输出电压和电动机实际端电压之间存在误差，因低速工况下电动机反电动势很小，此误差对控制性能的影响尤为明显。在轨道交通等低开关频率应用场合，在一个开关周期TPWM内存在多个控制周期T，并且在每个控制周期内都需进行电压高精度重构和电动机模型计算，因此需将逆变器关断延时和导通压降分离出来。

图2 两电平三相逆变器基本结构图Fig.2 Structure of two-level three phase inverter

图3 逆变器理论和实际输出脉冲示意图Fig.3 Output pulse for inverter in theory and real

逆变器开关器件的内阻Rm和电动机的初级绕组电阻Rs及线缆的电阻RL都会产生一定的压降，因此将其合在一起定义为新的电动机绕组电阻，即

首先测定R's，电动机A、B 相之间施加较大直流电流i1和i2，C 相不导通(即ia=－ib=i1，i2)，此时开关器件的内阻和电压误差可认为一致，A、B 相施加的电压分别为u1、u2，则有

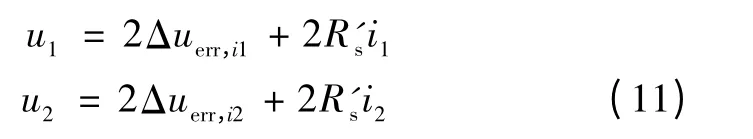
因此

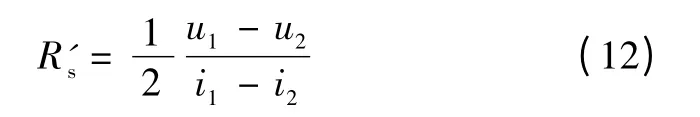
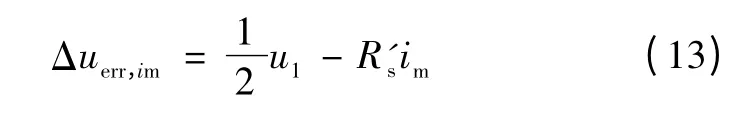
调节导通电流im的大小(im=1，2，…，imax)，分别得到与之对应的电压误差Δuerr，i1，Δuerr，i2，Δuerr，i3，…，Δuerr，imax，然后对电压误差进行曲线拟合，得到某型号IGBT 逆变器误差电压和导通电流的非线性关系，如图4所示。

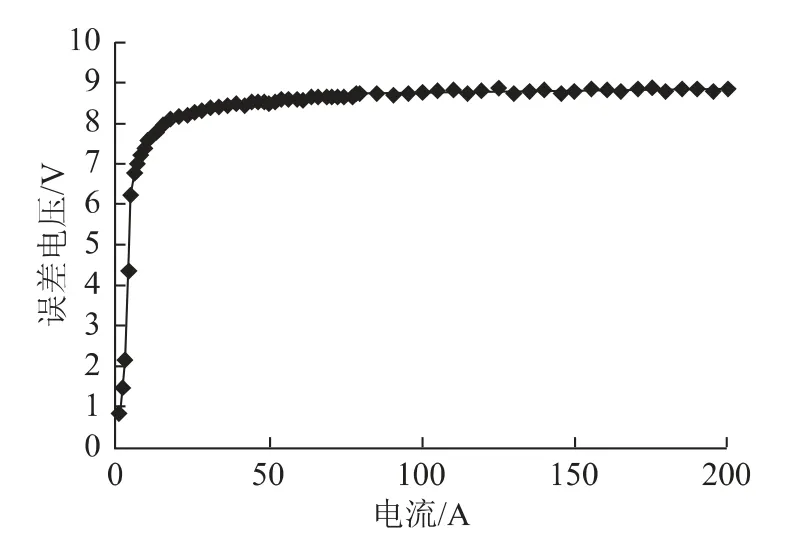
图4 逆变器误差电压和电流关系图Fig.4 Relation between inverter voltage error and current

根据器件特性可知，其开通延时基本恒定，死区时间为预先设定，器件关断延时和导通压降随器件通过电流的大小而变化。对施加不同电流大小时器件的关断延时进行测定，得到某型号IGBT 器件的关断延时，如图5所示。根据电压总误差和测定的IGBT 关断延时及导通时间则可得到器件的导通压降，如图6所示。通过分离得到器件的关断延时和导通压降，即可在每个控制周期内进行逆变器输出电压的高精度重构，以提升控制性能。

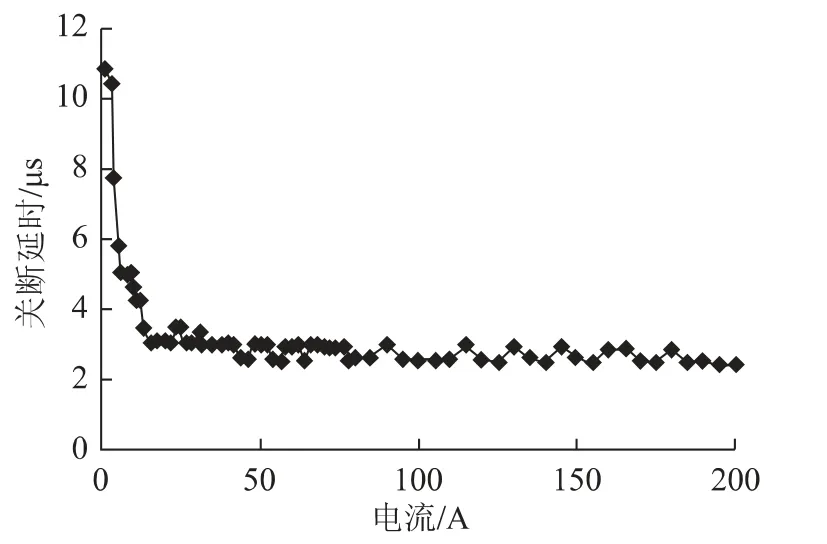
图5 关断延时和电流关系图Fig.5 Relation between turn-off-delay time and current

图6 导通压降和电流对应关系图Fig.6 Relation between collector-emitter voltage and current

3 次级电阻在线辨识算法研究

对直线电动机模型进行分析可知，在低速工况下电动机的输出推力和初、次级电阻及互感密切相关。其中互感参数与电动机运行速度和磁饱和程度相关，可在离线状态下进行测定，工作过程中查表得到实时值;初级绕组温度可通过温度传感器进行测量，次级绕组随环境温度的变化而变化，室外温度北方冬天会低至－30℃，夏天南方则会突破40℃，且早晚温差变化很大，因此次级绕组对低速工况下电动机推力输出的准确性起着至关重要的影响，需要进行在线实时辨识。低速工况下直线电动机动态边端效应可忽略不计，则其Γ 型等效电路如图7所示。

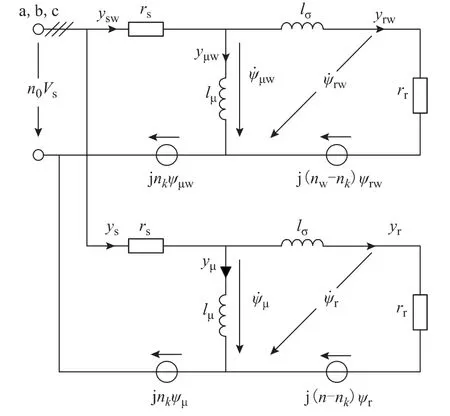
图7 电机Γ 型等效电路模型Fig.7 Equivalent Γ-circuit diagrams of motor

直线电动机电压方程和磁链方程为

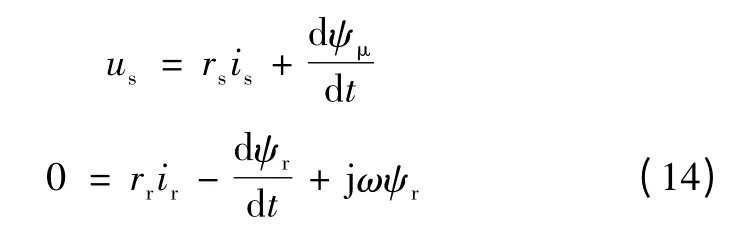
式中:us为初级电压;is、ir、ψμ、ψr、rs、rr分别为初级和次级的电流、磁链和电阻;ω 为次级速度。

初级电流方程为

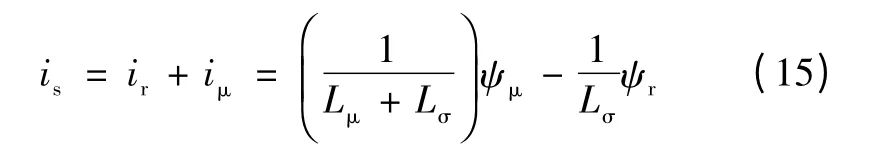
式中Lμ、Lσ分别为励磁电感和次级漏感。

为工程应用中参数调节方便，对电动机方程进行标幺处理，标幺基值见附录，得到电动机标幺方程为

令Δx=x -xw，Δys=ys-ysw，Δr=rr-rrw，带下标w 的变量表示为电动机相关量的实际值，如图7所示。

由式(16)可得

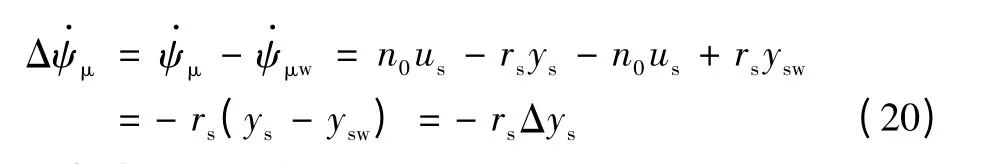
由式(17)可得

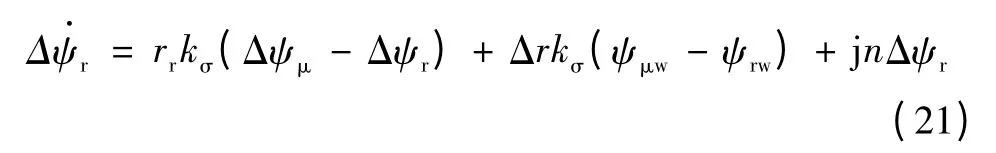
由式(18)可得

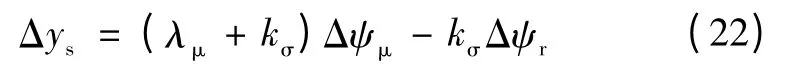
由式(19)可得

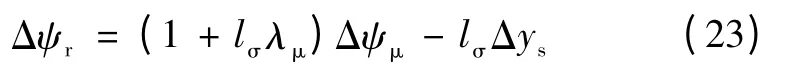
对式(22)进行微分得到

将式(20)、式(21)、式(23)代入式(24)可得

对式(25)进行微分得到

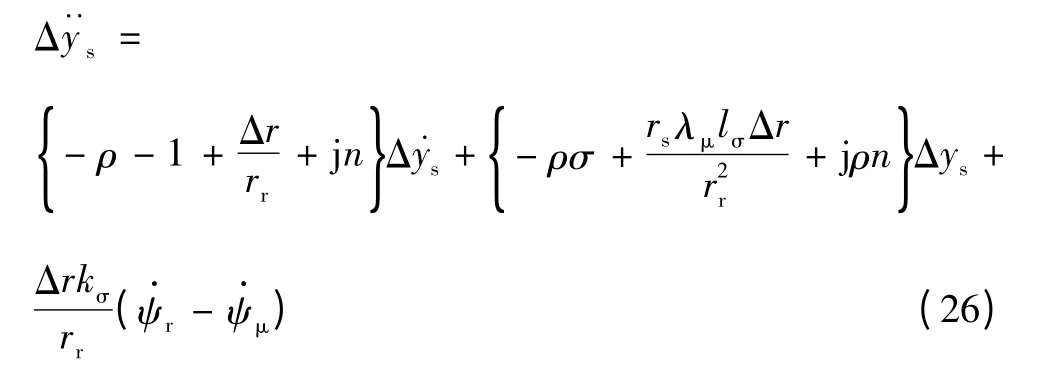
式(26)表达了电动机模型电流和电机实际电流之间的误差Δys与次级电阻误差Δr 之间的理论关系，是次级电阻辨识的理论基础。

电流的一阶导数和二阶导数可由电流本身及其频率ns表示，即代 入式(26)可得

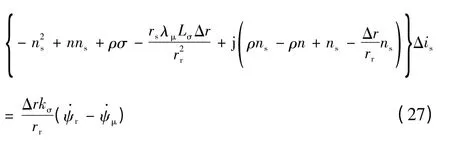
简化可得

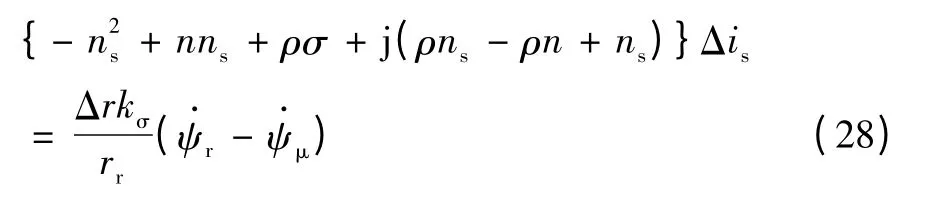
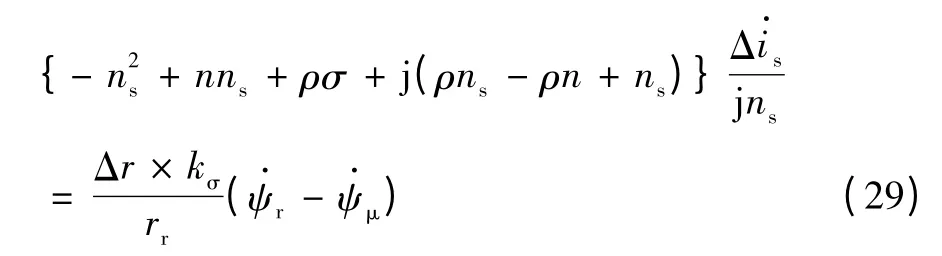
令Z 为

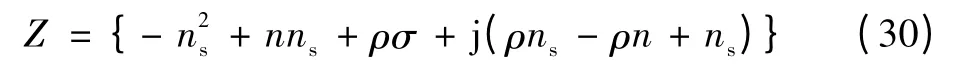
式(29)两边同时进行积分处理可得

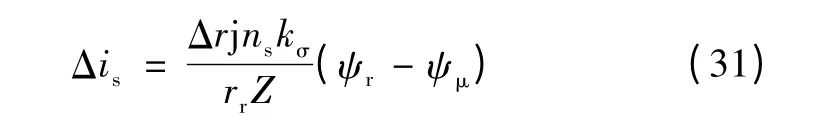
电流误差空间矢量Δis与(ψr- ψμ)*相乘则可得静止量，其值和Δr 呈对应关系

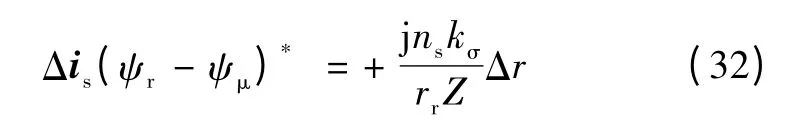
则可得次级电阻辨识自适应率为式(33)，次级电阻在线辨识算法框图如图8所示。

图8 次级电阻在线辨识框图Fig.8 Diagram of the secondary resistance estimation scheme

下面进行辨识算法的稳定性分析，由式(31)可知，如电动机处于空载运行工况，则转差nr=0，此时有ψr-ψμ=0，所以在空载条件下不能进行次级电阻的在线辨识。以nr=0．2，ns=-1～1(均为标幺值)为例进行全速度下的稳定性仿真分析，得到系数变化如图9所示，其值均为负数，所以其能保证全工况范围内的辨识收敛性(ns≠0，nr≠0)。变化图

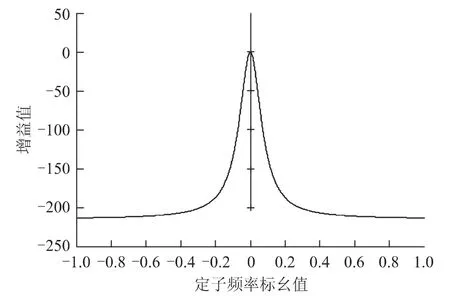
图9 全速度范围Fig.9 Value ofat full speed region

4 实验及分析

4.1 逆变器误差补偿实验

采用输出频率f 极低的电压开环控制方式，此时电动机可等效为纯电阻，输出为uα=Ucos(2πft)，uβ=Usin(2πft)(其中U 为设定的输出电压)，uα、uβ进行SVPWM 调制得到逆变器三相脉冲控制信号。根据电动机等效电阻R's可计算出逆变器的理论输出电流，同时对电动机实际电流进行采集，逆变器非线性误差的补偿效果可由两者的吻合程度来表征。

只考虑逆变器死区补偿时得到的实验波形如图10所示，电动机三相实际电流和A 相理论电流分别如图中所示。实验数据表明:只进行死区补偿时，理论电流和实际电流的吻合度较差，且电动机三相电流正弦性较差，存在畸变。因未进行开关器件导通延时的补偿，所以造成器件实际导通时间较理论导通时间长，也即逆变器实际输出电压大于理论输出电压，所以出现了图中实际输出电流大于理论电流的实验结果。

图10 考虑死区补偿的电动机理论和实际电流Fig.10 Motor currents in theory and real with dead-time compensation

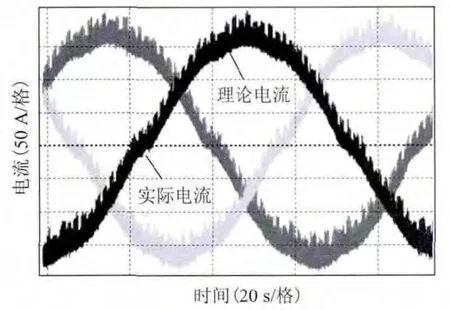
图11 考虑死区、关断延时和导通压降补偿的电动机理论和实际电流Fig.11 Motor currents in theory and real with dead time，turn off delay time and collector-emitter voltage compensation

同时进行死区、关断延时以及导通压降补偿时的实验波形如图11所示，理论电流和实际电流吻合度非常高，基本重合，且实际电流正弦性很好，实验数据表明逆变器非线性误差补偿的效果非常好，说明逆变器实际输出电压与理论电压几乎一致。

4.2 次级电阻在线辨识实验

基于某地铁项目直线电动机进行了堵转工况下的次级电阻在线辨识算法的实验，电动机基本参数如附录所示。施加一定的推力指令，同时对电动机实施机械抱闸制动，将次级电阻初值设为0.12(实验波形中为观测方便，将值放大了500 倍)，然后起动在线辨识算法，得到实验波形如图12所示，辨识值快速收敛于0.23 并保持恒定，根据当时的环境温度可推算，辨识值的误差约为7℃。

图12 次级绕组在线辨识波形Fig.12 Waveform for secondary resistance estimation

4.3 某地铁项目现场低速运行实验

基于本文所提低速速度观测算法，对某地铁项目进行了列车起动和制动停车实验。起动波形如图13所示，制动过程波形如图14所示。实验波形表明，在低速起动和制动过程中，转速观测值连续且波动在1 r/min 以内，观测速度能够很好的反应列车真实运行速度，电流波形规则且正弦性好。在ATO 自动驾驶模式下，从未出现车辆冲标或欠标的行车事故，直接证明了所提算法的可行性。

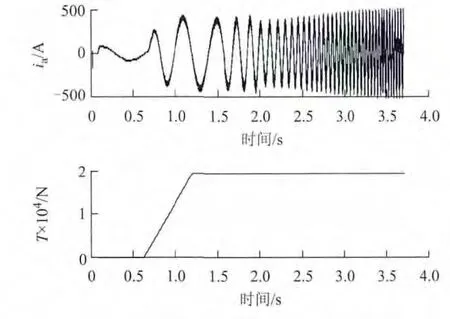
图13 低速起动波形Fig.13 Waveform for starting at low speed

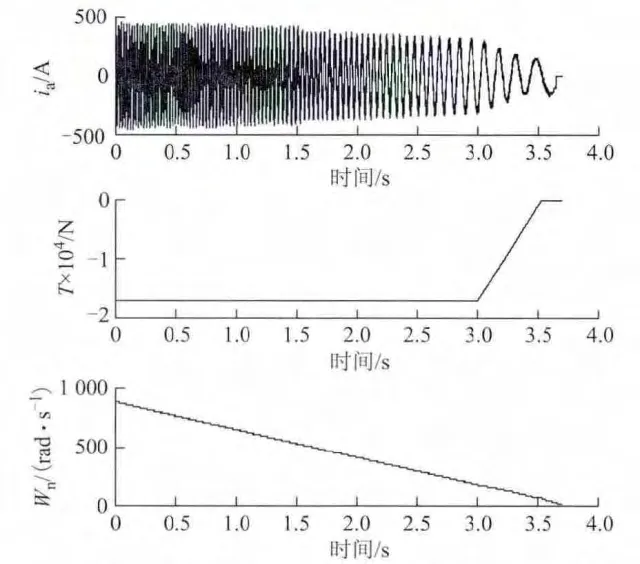
图14 低速制动波形Fig.14 Waveform for braking at low speed

5 结论

直线感应电动机驱动的列车低速运行时，传感器输出脉冲之间的时间间隔很长，传统的M、T 测速法未能精确地检测列车瞬时速度，导致低速工况下控制性能较差。本文提出了一种基于牛顿运动模型的瞬时速度观测算法，并对影响低速观测精度的逆变器非线性误差以及电动机参数非线性时变等因素进行了深入分析，提出了一种适应于低开关频率应用场合的逆变器误差补偿算法，并基于电动机本体方程提出了一种能保证稳定性的次级电阻在线辨识算法。在某地铁项目自主研发的直线电动机牵引系统上完成了算法的实验验证，并进行了工程化应用，系统于2013年初开始正式载客运营，系统运行可靠、稳定。

附 录

标幺基本值:

基本频率系数n0=ω0Tσ

电动机参数:

次级电阻Rr=0.210 7 Ω

初级电阻Rs=0.109 Ω

初级漏感Lls=3.6 mH

次级漏感Llr=0.034 mH

电动机极对数p=4

电动机极距τ=0.280 8 m

［1］ Nonaka S，Higuchi T．Design of single-sided linear induction motors for urban transit［J］．IEEE Transactions on Vehicular Technology，1988，37(3):167-173．

［2］ Morizane T，Tsujikawa K，Kimura N．Control of traction and levitation of linear induction motor driven by power source with frequency component synchronous with the motor speed［J］．IEEE Transactions on Magnetics，2011，47(10):4302-4305．

［3］ Wai R J，Lee J D．Dynamic analysis and stabilizing control of linear magnetic-levitation rail system［C］．33rdAnnual Conference of the IEEE Industrial Electronics Society，Taipei，2007:2213-2218．

［4］ 徐伟，汪旭东，袁世鹰．交通牵引大功率单边直线感应电机性能研究［J］．电机与控制学报，2008，12(4):396-402．

Xu Wei，Wang Xudong，Yuan Shiying．Performance research on high power single linear induction motor in tractive transportation［J］．Electric Machines and Control，2008，12(4):396-402．

［5］ 王旭，刘志，龙志强．磁浮列车测速定位方法综述［J］．兵工自动化，2008，27(1):69-72．

Wang Xu，Liu Zhi，Long Zhiqiang．Survey on speed measuring and locating method of maglev train［J］．O．I．Automation，2008，27(1):69-72．

［6］ Tsuji T，Mizuochi M，Nishi H，et al．A velocity measurement method for acceleration control［J］．Industrial Electronics Society，2005(6):1943-1948．

［7］ Madeti A，Tilak K，Bidi N，et al．Model-based wheel speed acquisition by interrupt capture method for integrated stability control［C］．Fifth International Conference on Sensing Technology，Palmerston North，2011:660-665．

［8］ 邓江明，陈特放，唐建湘，等．单边直线感应电机的无速度传感器虚拟控制［J］．中国电机工程学报，2012，32(27):53-59．

Deng Jiangming，Chen Tefang，Tang Jiangxiang，et al．Virtual speed sensorless desired control strategy of maglev single-sided linear induction motors［J］．Proceedings of the CSEE，2012，32(27):53-59．

［9］ Accetta A，Cirrincione M，Pucci M，et al．Neural sensorless control of linear induction motors by a fullorder luenberger observer considering the end effects［J］．IEEE Transactions on Industry Application，2014，50(3):1891-1904．

［10］ 杨兴华，姜建国．永磁同步电机精确瞬时速度检测［J］．电工技术学报，2011，26(4):71-76．

Yang Xinghua，Jiang Jianguo．Precise instantaneous speed detection for permanent magnet synchronous motor［J］．Transactions of China Electrotechnical Society，2011，26(4):71-76．

［11］ 郑泽东，李永东，肖曦，等．永磁电机负载转矩观测器［J］．电工技术学报，2010，25(2):30-36．

Zheng Zedong，Li Yongdong，Xiao Xi，et al．Load torque observer of permanent magnet synchronous motor［J］．Transactions of China Electrotechnical Society，2010，25(2):30-36．

［12］ Kweon T J，Hyun D S．High performance speed control of electric machine using low-precision shaft encoder［J］．IEEE Transactions on Power Electronics，1999，14(5):838-849．

［13］ Su Y X，Zheng C H，Mueller P C，et al．A simple improved velocity estimation for low-speed regions based on position measurement only［J］．IEEE Transactions on Control Systems Technology，2006，14(5):937-942．

［14］ Kovudhikulrungsri L，Koseki T．Precision speed estimation from a low-resolution encoder by dual-sampling-rate observer［J］．IEEE Transactions on Mechatronics，2006，11(6):661-670．

［15］ Lee K，Blaabjerg F．Robust and stable disturbance observer of servo system for low-speed operation［J］．IEEE Transactions on Industry Application，2007，43(3):627-635．

［16］ 吴茂刚，赵荣祥，汤新舟．空间矢量PWM 逆变器死区效应分析与补偿方法［J］．浙江大学学报(工学版)，2006，40(3):469-473．

Wu Maogang，Zhao Rongxiang，Tang Xinzhou．Analysis and compensation method of dead time effect for space vector PWM inverter［J］．Journal of Zhejiang University(Engineering Science )，2006，40(3):469-473．

［17］ 王高林，李卓敏，詹瀚林，等．考虑逆变器非线性的内置式永磁同步电机转子位置锁相环观测器［J］．电工技术学报，2014，29(3):172-179．

Wang Gaolin，Li Zhuomin，Zhan Hanlin，et al．Phaselocked-loop rotor position observer for IPMSM considering inverter nonlinearity［J］．Transactions of China Electrotechnical Society，2014，29(3):172-179．

［18］ 王高林，于泳，杨荣峰，等．感应电机空间矢量PWM 控制逆变器死区效应补偿［J］．中国电机工程学报，2008，28(15):79-83．

Wang Gaolin，Yu Yong，Yang Rongfeng，et al．Deadtime compensation of space vector PWM inverter for induction motor［J］．Proceedings of the CSEE，2008，28(15):79-83．

［19］ Pellegrino G，Bojoi R I，Guglielmi P，et al．Accurate inverter error compensation and related self-commissioning scheme in sensorless induction motor drives［J］．IEEE Transactions on Industry，2010，46(5):1970-1978．

［20］ Silva C，Araya R．Sensorless vector control of induction machine with low speed capability using MRAS with drift and inverter nonlinearities compensation［C］．The International Conference on“Computer as a Tool”，Copenhagen，Denmark，2007:1922-1928．

［21］ Choi C H，Cho K R，Seok J K．Inverter nonlinearity compensation in the presence of current measurement errors and switching device parameter uncertainties［J］．IEEE Transactions on Power Electronics，2007，22(2):576-583．

［22］ Raute R，Caruana C，Staines C S，et al．Analysis and compensation of inverter nonlinearity effect on a sensorless PMSM drive at very Low and zero speed operation［J］．IEEE Transactions on Industrial Electronics，2010，57(12):4065-4074．

［23］ Zhao Hengbing，Wu Q M J，Kawamura A．An accuracy approach of nonlinearity compensation for VSI inverter output voltage［J］．IEEE Transactions on Power Electronics，2004，19(4):1029-1035．

［24］ 徐伟，孙广生，李耀华，等．一种新型的直线异步电机参数测量方案［J］．电工技术学报，2007，22(6):54-58．

Xu Wei，Sun Guangsheng，Li Yaohua，et al．A new parameter measurement scheme for single linear induction motors［J］．Transactions of China Electrotechnical Society，2007，22(6):54-58．

［25］ 王高林，杨荣峰，于泳，等．无速度传感器异步电机转子磁场定向自适应鲁棒控制［J］．电工技术学报，2010，25(10):73-80．

Wang Gaolin，Yang Rongfen，Yu Yong，et al．Adaptive robust control for speed sensorless field-oriented controlled induction motor drives［J］．Transactions of China Electrotechnical Society，2010，25(10):73-80．

［26］ 刘艳，齐晓艳．感应电机龙伯格-滑模观测器参数辨识方法［J］．电机与控制学报，2011，15(8):93-100．

Liu Yan，Qi Xiaoyan．An luerberger-sliding mode observer parameter identification for induction motors［J］．Electric Machines and Control，2011，15(8):93-100．

［27］ 徐奇伟，宋立伟，崔淑梅．感应电机矢量控制中转子参数自适应辨识［J］．电工技术学报，2011，26(6):81-87．

Xu Qiwei，Song Liwei，Cui Shumei．Induction motor vector control based on adaptive identification of rotor parameters［J］．Transactions of China Electrotechnical Society，2011，26(6):81-87．

［28］ 范蟠果，杨耕．感应电机无速度传感器控制自适应速度观测器［J］．电机与控制学报，2008，12(6):621-628．

Fan Panguo，Yang Geng．Adaptive speed observer for speed sensorless control of induction motor［J］．Electric Machines and Control，2008，12(6):621-628．

［29］ 黄进，赵力航，刘赫．基于二阶滑模与定子电阻自适应的转子磁链观测器及其无速度传感器应用［J］．电工技术学报，2013，28(11):54-61．

Huang Jin，Zhao Lihang，Liu He．Sensorless control with resistance variation approach based on parallel MARS and second-order siding mode observer［J］．Transactions of China Electrotechnical Society，2013，28(11):54-61．

［30］ Kubota H，Tamura Y．Stator resistance estimation for sensorless induction motor drives under regeneration condition［C］．IEEE 2002 28thAnnual Conference Industrial Electronics Society，Sevilla，Spain，2002:426-430．