一种基于确定度的决策概率转换方法

赵玉新，贾韧锋，刘厂

（哈尔滨工程大学自动化学院，黑龙江哈尔滨150001）

一种基于确定度的决策概率转换方法

赵玉新，贾韧锋，刘厂

（哈尔滨工程大学自动化学院，黑龙江哈尔滨150001）

针对现有将基本概率赋值转换为决策概率方法的不足，提出一种基于确定度的决策概率转换方法。该方法根据基本概率赋值的特点，将单子集命题的基本概率赋值之和作为系统对命题的确定度，并用其对比例信度转换方法和比例似真度转换方法进行线性组合，得出命题的决策概率。通过算例对比新方法与已有方法，结果表明新方法更加合理有效。

确定度；基本概率赋值；信度；似真度；决策概率

证据理论是Dempster［1］于1967年首先提出，后经他的学生Shafer［2］进一步扩充和完善，所以通常被称作Dempster⁃Shafer理论（简称D⁃S证据理论）。由于D⁃S证据理论在处理不确定、不精确信息方面，具有较大的灵活性，因而被广泛应用在威胁判断［3］、故障诊断［4］、信息融合［5］、风险评估［6⁃7］等诸多领域。D⁃S证据理论在识别框架下用基本概率赋值（basic probability assignment，BPA）来对命题进行表示，这种表示方法不仅通过在单子集命题上分配概率来表示精确信息；也通过在多子集命题上分配概率来表示不精确信息，能够比较全面地表达命题信息。在不确定决策系统中，为了能够合理地做出决策，需要将多子集命题上的BPA分配给单子集命题，以便得到合适的决策概率，这就需要对BPA进行决策概率转换。

目前，对BPA进行决策概率转换的方法有很多［8⁃19］。Smets［8］在可转移信度模型中提出了转换方法，但该方法没有很好地利用已知信息，将多子集命题上的BPA均分到单子集命题上，容易造成信息损失，不利于决策。Cuzzolin［9］的方法是将多子集命题上的BPA按照不确定比均分给单子集命题，该方法在Ai∩A＝∅时，不能合理地分配不确定信息。例如已知识别框架Θ＝A，B，C{}，其中有m（A∪B）＞0，在计算C的决策概率时，TNSM中的m（A∪B），也会按照比例分给C，这明显是不合理的，因为A∪B中不包括C。Cobb［10］提出了基于似真度函数的转换，该方法仅仅将各个命题的似真度所占的比例作为它们的决策概率，而没有考虑信度对转换过程的影响，转换过程比较保守。Sudano［14］在DST框架下，利用信度函数和似真度函数提出了一系列的转换方法。蒋雯［15］利用命题的信度和似真度的特点，对多子集命题信息进行分配，但是当多子集命题和单子集命题没有交集的时候，也会出现Cuzzolin方法中的不合理分配问题。Dezert［18］的方法是可转移信度模型中转换方法和比例信度转换方法的非线性组合，通过调整参数ε来决定转换态度，灵活度较好，但参数ε的选取不够客观。Daniel［19］的比例信度转换方法利用单子集命题在多子集命题中的信度比来转换决策概率，转换时的态度比较乐观，容易增大决策风险。而他的比例似真度转换方法利用单子集命题在多子集命题中的似真度比来转换决策概率，转换时的态度又比较保守，不利于决策。

本文针对Daniel的比例转换方法的不足，提出了一种基于确定度的决策概率转换方法。该方法将单子集命题的基本概率赋值之和作为系统对命题的确定度，并用其对比例信度转换方法和比例似真度转换方法进行线性组合，得出命题的决策概率。

1 基于确定度的决策概率转换方法

为了更好地发挥比例信度转换方法和比例似真度转换方法的优势，克服它们的不足，本文对这2种方法进行线性组合，使转换时的态度既不乐观也不保守，得出合理的决策概率。

由于单子集命题的基本概率赋值反映了系统对命题的精确信任程度，单子集命题的基本概率赋值越大，说明系统对该命题的确定程度也就越高；单子集命题的基本概率赋值越小，说明系统对该命题的确定程度也就越低。所以，根据系统的局部与整体之间的相似性质，可以将单子集命题的基本概率赋值之和作为系统对命题的确定度，并将该确定度作为组合权重，用来对比例信度转换方法和比例似真度转换方法进行线性组合，得出命题的决策概率。当系统对命题的确定度大时，转换过程的态度应该相对乐观，反之，转换时的态度应该保守一些。

根据前面所述，本文方法的转换公式如下：

式中：

因为A是单子集命题，所以式（1）也可以写成：

Daniel在文献［20］中给出了决策概率转换函数PT（·）的定义，下面通过该定义对本文方法的合理性进行说明。

式（3）可以转化为

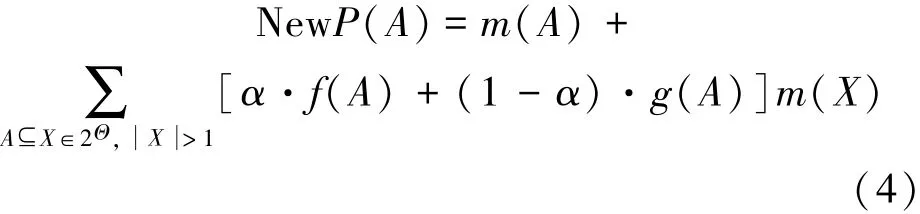
定理1 PT（·）需满足上下边界一致性，即

所以，Bel（A）≤P1（A）≤Pl（A），同理可证，Bel（A）≤P2（A）≤Pl（A），又因为，NewP（A）是P1（A）和P2（A）的线性组合，所以，Bel（A）≤NewP（A）≤Pl（A）。

推论1 针对贝叶斯BPA，PT（·）需满足概率一致性，即

证明：因为，m（A）是贝叶斯BPA，所以，m（X）＝0，所以，由式（4）可得，NewP（A）＝m（A）。

推论2 对于不可能事件A，PT（·）需满足：

证明：因为，A为不可能事件，

所以，Bel（A）＝0，Pl（A）＝0，

所以，由Bel（A）≤NewP（A）≤Pl（A）可得，NewP（A）＝0。

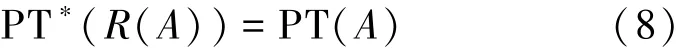
即Θ中的元素A经过排列函数R作用后的像R（A）的决策概率PT∗（R（A）），和A在排列函数R作用前的决策概率PT（A）相等。

证明：因为，R为从Θ→Θ∗的排列函数，

所以，R（A）＝A，

所以，R（A）的基本概率赋值m∗（R（A））＝m（A），所以，NewP∗（R（A））＝m∗（R（A））+g（A）］m（X）＝NewP（A）。

综上所述，本文方法满足Daniel给出的决策概率转换函数定义。

2 决策概率转换评价标准

由于多子集命题是对单子集命题支持的一种表现，决策概率转换是将这种表现给予了量化。所以可以利用它们之间的这种内在联系，来评价转换方法的优劣。本文引入随机变量的关联系数的概念［21］，将单子集命题的BPA和转换后的决策概率之间的关联系数，用于度量转换后的决策概率与原BPA之间的关联程度，也依此作为评价转换方法好坏的标准。关联系数越大，说明转换后的决策概率与原BPA之间的关联程度也就越好，也就越能反映原BPA的信息，转换方法也就越好。

定义1设随机变量X与Y的分布为

随机变量X关于随机变量Y的偏熵定义为

定义2 随机变量X与Y之间的关联熵定义为它们的偏熵之和，即

定义3 随机变量X与Y的偏关联系数与关联系数分别定义为

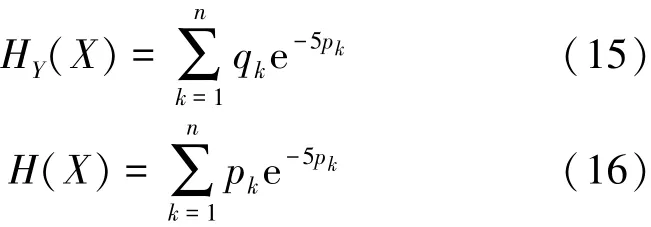
3 实例分析

例1 现用一雷达传感器观测空中的飞行目标，其观测到的结果可能有F⁃15和Mig⁃27，则它们构成的识别框架Θ＝｛θ1，θ2｝，其中θ1、θ2分别代表F⁃15、Mig⁃27，根据观测数据可知它们的基本概率赋值如下：

根据本文的方法进行如下计算：

1）根据比例信度转换决策概率的方法，分别计算θ1、θ2的决策概率P1（θ1）、P1（θ2）：

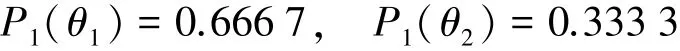
2）根据比例似真度转换决策概率的方法，分别计算θ1、θ2的决策概率P2（θ1）、P2（θ2）：

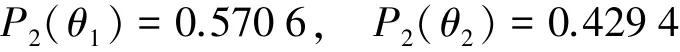
3）分别对P1（θ1）和P2（θ1）、P1（θ2）和P2（θ2）进行线性组合，得出θ1、θ2最终的决策概率P（θ1）、P（θ2）。

首先，按照式（2）计算α＝0.2+0.1＝0.3。

然后，按照式（1）计算θ1、θ2最终的决策概率P（θ1）＝0.599 4， P（θ2）＝0.400 6。

例2 和例1在同一识别框架Θ＝｛θ1，θ2｝下，另有一组通过ESM传感器获得的基本概率赋值如下：

m（θ1）＝0.8， m（θ2）＝0.1， m（θ1∪θ2）＝0.1

按照本文方法计算结果如表1所示，并在表1中将例1的结果和例2的结果进行对比。

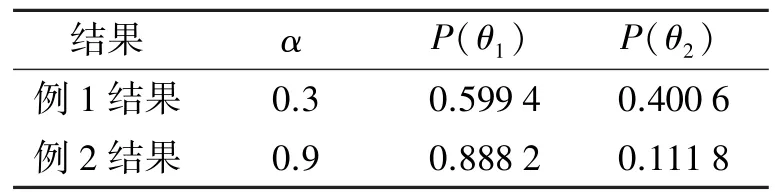
表1 例1结果和例2结果对比Table 1 The comparison between example 1 and example 2

例1和例2虽属于同一识别框架，但由于传感器的精度不同，得到的结果也不同。通过计算m（θ1∪θ2）在θ1和θ2上的分配比，很容易看到例1中的分配比（0.5994-0.2）／（0.4006-0.1）＝1.3287，小于例2的（0.8882-0.8）／（0.1118-0.1）＝7.474 6。那是因为例2中确定度α＝0.9，大于例1中的确定度α＝0.3。可见，当系统对命题的确定度越高，转换结果就较为乐观，分配多子集命题上的BPA也就越多；当系统对命题的确定度越低，转换结果就较为保守，分配多子集命题上的BPA也就越少。

例3现对一风力发电机组进行故障诊断，通过分析可知该发电机组可能发生的故障有主轴故障θ1、发电机故障θ2、叶片故障θ3、齿轮箱故障θ4，它们构成的识别框架Θ＝｛θ1，θ2，θ3，θ4｝，经专家测评得到该框架下的基本概率赋值如下：

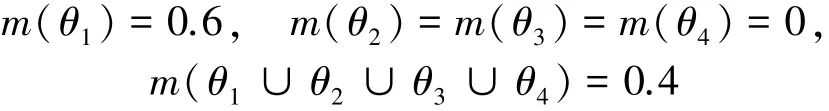
按照本文方法计算的结果如表2所示，并且在表2中将本文方法与其他常用方法进行了对比，由于DSmP方法中参数ε的选取不易确定，这里取中间值ε＝0.5。

从表2的结果可以看出，该例中的几种方法得到的结果都是主轴故障的决策概率最大。PFT方法和PrNPl方法得到主轴故障的决策概率P（θ1）＝0.454 5＜m（θ1）＝0.6，这明显是不合理的。Prop⁃BelP方法和PrBel方法得到的结果，看起来是最理想的，但是由于不确定度的存在，θ1∪θ2∪θ3∪θ4上的BPA不应该全分配给故障θ1，也应该分配给故障θ2、θ3和θ4一些，所以这2种方法得到的结果也不合理。本文方法的关联系数高于其他常用方法的关联系数，说明本文方法得到的转换结果和原BPA之间的关联程度更大，更能反映原BPA中的信息。并且本文方法得到主轴故障的决策概率P（θ1）＝0.912 7，要远大于其他故障的决策概率P（θ2）＝P（θ3）＝P（θ4）＝0.029 1，比其他常用方法得到的结果更一目了然，更利于决策。

表2 本文方法与其他常用方法对比Table 2 The comparison of different methods

4 结束语

本文提出的决策概率转换方法充分利用了已知信息，将系统对命题的确定度作为组合权重，能够客观地、合理地分配多子集命题上的信息，使转换时的态度既不乐观也不保守，得到的转换结果更加合理有效。该方法能够增加决策的准确度，降低决策风险，便于决策者做出合理的决策，可以较好地应用到信息融合、故障诊断等诸多的辅助决策系统中。

［1］DEMPSTER A P.Upper and lower probabilities induced by a multivalued mapping［J］.Annals of Mathematical Statis⁃tics，1967，38（2）：325⁃339.

［2］SHAFER G.A mathematical theory of evidence［M］.［S.l.］：Princeton University Press，1976：815⁃90.

［3］黄文斌，陈颜辉.基于D⁃S证据理论的潜艇威胁判断方法研究［J］.哈尔滨工程大学学报，2005，26（2）：164⁃168.HUANG Wenbin，CHEN Yanhui.Research on methods in submarine threat estimation based on D⁃S evidence theory［J］.Journal of Harbin Engineering University，2005，26（2）：164⁃168.

［4］LUO H，YANG S L，HU X J，et al.Agent oriented intelli⁃gent fault diagnosis system using evidence theory［J］.Expert Systems with Applications，2012，39（3）：2524⁃2531.

［5］LEUNG Y，JI N N，MA J H.An integrated information fusion approach based on the theory of evidence and group decision⁃making［J］.Information Fusion，2013，14（4）：410⁃422.

［6］LI B，PANG F W.An approach of vessel collision risk as⁃sessment based on the D⁃S evidence theory［J］.Ocean Engi⁃neering，2013，74：16⁃21.

［7］YANG J P，HUANG H Z，HE L P，et al.Risk evaluation in failure mode and effects analysis of aircraft turbine rotor blades using Dempster⁃Shafer evidence theory under uncer⁃tainty［J］.Engineering Failure Analysis，2011，18（8）：2084⁃2092.

［8］SMETS P，KENNES R.The transferable belief model［J］.Artificial Intelligence，1994，66（24）：191⁃234.

［9］CUZZOLIN F.On the properties of the intersection probabili⁃ty［EB／OL］.（2007）［2014⁃03⁃01］.http：／／perception.inri⁃alpes.fr／people／Cuzzolin.

［10］COBB B R，SHENOY P P.On the plausibility transforma⁃tion method for translating belief function models to proba⁃bility models［J］.International Journal of Approximate Reasoning，2006，41（3）：314⁃330.

［11］许培达，韩德强，邓勇.一种基本概率赋值转换为概率的最优化方法［J］.电子学报，2011，39（3A）：121⁃125.XU Peida，HAN Deqiang，DENG Yong.An optimal trans⁃formation of basic probability assignment to probability［J］.Acta Electronica Sinica，2011，39（3A）：121⁃125.

［12］HU L F，HE Y，GUAN X，et al.A new probabilistic trans⁃formation in generalized power space［J］.Chinese Journal of Aeronautics，2011，24（4）：449⁃460.

［13］王万请，赵拥军，黄洁，等.基于不确定度的基本概率赋值概率转换方法［J］.控制与决策，2013，28（8）：1214⁃1218.WANG Wanqing，ZHAO Yongjun，HUANG Jie，et al.Transformation of basic probability assignment to probability based on uncertainty degree［J］.Control and Decision，2013，28（8），1214⁃1218.

［14］SUDANO J J，MARTIN L.Pignistic probability transforms for mixs of low⁃and high⁃probability events［C］／／Fourth In⁃ternational Conference on Information Fusion 2001.Montre⁃al，Canada，2001：23⁃27.

［15］蒋雯，吴翠翠，贾佳，等.D⁃S证据理论中的基本概率赋值转换概率方法研究［J］.西北工业大学学报，2013，31（2）：295⁃299.JIANG Wen，WU Cuicui，JIA Jia，et al.A probabilistic transformation of basic probability assignment（BPA）in D⁃Sevidence theory［J］.Journal of Northwestern Polytech⁃nical University，2013，31（2），295⁃299.

［16］HU L F，HE Y，GUAN X，et al.New probabilistic trans⁃formation of imprecise belief structure［J］.Journal of Sys⁃tems Engineering and Electronics，2011，22（5）：721⁃729.

［17］SUDANO J J，MARTIN L.Yet another paradigm illustra⁃ting evidence fusion（YAPIEF）［C］／／9th International Conference on Information Fusion.Florence，2006.

［18］DEZERT J，SMARANDACHE F.A new probabilistic trans⁃formation of belief mass assignment［C］／／11th International Conference on Information Fusion.Cologne，2008.

［19］DANIEL M.Consistency of probabilistic transformations of belief functions［C］／／Proceedings of the Tenth Internation⁃al Conference IPMU.Perugia，2004：1135⁃1142.

［20］DANIEL M.Probabilistic transformations of belief functions［C］／／Symbolic and Quantitative Approaches to Reasoning with Uncertainty.Perugia，2005：539⁃551.

［21］吴敏金，白治江.关联熵及其应用［J］.华东师范大学学报：自然科学版，1998（2）：28⁃35.WU Minjin，BAI Zhijiang.Relative entropy and its applica⁃tion［J］.Journal of East China Normal University：Natural Science，1998（2）：28⁃35.

［22］邓勇，王栋，李齐，等.一种新的证据冲突分析方法［J］.控制理论与应用，2011，28（6）：839⁃844.DENG Yong，WANG Dong，LI Qi，et al.A new method to analyze evidence conflict［J］.Control Theory and Applica⁃tions，2011，28（6）：839⁃844.

Transformation method of decision-making probability based on the certainty degree

ZHAO Yuxin，JIA Renfeng，LIU Chang

（College of Automation，Harbin Engineering University，Harbin 150001，China）

In order to overcome the drawbacks in current transformation methods of basic probability assignment to decision⁃making probability，a decision⁃making probability transformation method based on the certainty degree is proposed.According to the characteristic of basic probability assignment，the sum of each the Singleton proposition' s basic probability assignments is regarded as the certainty degree of the system in this paper，and the decision⁃making probability of each proposition was achieved by linear combination，which is the transformation method of decision⁃making probability based on proportional belief and proportional plausibility.The proposed method was compared to the other usual methods with examples.The experimental results show that the proposed method is more reasonable and effective.

certainty degree；basic probability assignment；belief；plausibility；decision⁃making probability

但是，当有变量值为0的时候，上述计算就会出现log0＝-∞的情况，为此邓勇等人在文献［22］中提出了一种类熵的概念，较好地解决了这个问题。即随机变量X关于随机变量Y的类偏熵定义为

10.3969／j.issn.1006⁃7043.201404042

TP391

：A

：1006⁃7043（2015）06⁃0801⁃05

http：／／www.cnki.net／kcms／detail／23.1390.u.20150428.1115.016.html

2014⁃04⁃12.网络出版时间：2015⁃04⁃28.

国家自然科学基金资助项目（51379049）；中央高校基本科研业务费专项资金资助项目（HEUCFX41302，HEUCF041410）；黑龙江省留学归国人员科学基金资助项目（LC2013C21）.

赵玉新（1980⁃），男，教授，博士生导师；贾韧锋（1987⁃），男，博士研究生.

贾韧锋，E⁃mail：jiarenfeng＠hrbeu.edu.cn.