抑制相关噪声的水下图像恢复算法
肖易寒,庞永杰,赵蓝飞
(1.哈尔滨工程大学信息与通信工程学院,黑龙江哈尔滨150001;2.哈尔滨工程大学水下机器人技术重点实验室,黑龙江哈尔滨150001)
抑制相关噪声的水下图像恢复算法
肖易寒1,庞永杰2,赵蓝飞1
(1.哈尔滨工程大学信息与通信工程学院,黑龙江哈尔滨150001;2.哈尔滨工程大学水下机器人技术重点实验室,黑龙江哈尔滨150001)
由于传统算法无法消除相关噪声对于水下于图像的影响,通过最大后验估计构造了一个具有凸函数性质的变分模型用于抑制水下图像的相关噪声。在变分模型中通过贝叶斯约束项限定噪声的概率分布;采用马尔可夫约束项保证恢复图像满足空间连续性;通过梯度法获得变分模型的最优解,即不含相关噪声的恢复图像。实验结果表明,该算法能够有效地消除相关噪声,恢复图像的主观视觉效果较好。
水下图像;相关噪声;变分模型;梯度法
由于水下拍摄环境较为复杂,普通的CCD或者CMOS传感器所获取的数字图像容易受到相关噪声的影响[1]。这种由相关噪声所导致的图像退化现象不仅会对人眼的主观视觉产生一定程度的影响,而且这种现象会影响到模式识别系统的后续步骤,例如边缘检测、图像分割、目标检测与识别等算法的准确性。因此,如何有效的去除相关噪声已经成为水下图像处理领域的一个热点问题[2]。
经典的滤波算法例如均值滤波[3],中值滤波[4],双边滤波[5]等滤波算法只能消除加性噪声对于图像的影响。对于相关噪声,以上几种算法的噪声抑制效果较差。一些较为流行的去除相关噪声方法有小波变换[6],惩罚加权最小二乘(penalized weighted least squares,PWLS)方法[7]、LEE滤波器[8]、形状自适应余弦变换(shape⁃adaptive transform discrete cosine transform,SA⁃DCT)[9]等方法。虽然这几种方法能够在一定程度上抑制相关噪声对于图像的影响,但是恢复图像存在细节保持能力较差、图像降质、噪声抑制效果不佳等缺陷[10]。
为了有效地消除相关噪声,本文在最大后验估计的基础上构建了一个抑制相关噪声的、具有凸函数性质的变分模型,该模型既能够限定噪声的概率分布性质,又能够保证恢复图像的空间连续性。通过梯度法得到变分模型对应的不含噪声的、具有一定细节保持能力的恢复图像。
1 梯度法求解变分模型原理
1.1 相关噪声的数学模型
假设Z是包含相关噪声的总体,Z1,Z2,…,ZN为Z的N个独立的观测值,不包含噪声的图像可以表示为L,L1,L2,…,LN为L的N个独立的观测值。因此,包含相关噪声的退化图像模型通常可以表示为[11]
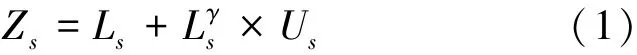
为了便于计算,此处将公式转化为加性噪声的形式:

式中:γ^
s为γ的等价的参数。将式(1)、(2)联立得到γ^
s的表达式:
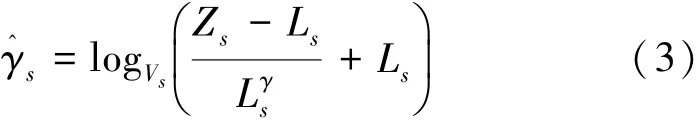
通过这种形式的变换可以将相关噪声转化为加性噪声。
1.2 基于图像子块的参数估计方法
根据式(1)可知,图像传感器模型中包含2个未知的参数,分别是指数部分的参数γ和高斯噪声的方差,通常情况下这2个参数都是未知的[13]。因此,抑制传感器噪声的图像恢复算法首先需要得到这2个参数的最优估计,从而实现非监督图像恢复算法。本文采用基于图像子块的参数估计算法对γ和进行估计[13],该算法的核心思想是找到了一组具有近似均匀、同质性的图像子块序列,通过计算同质子块的局部统计量从而得到未知参数的估计值。
算法原理如下:根据式(1),可以得到V的局部方差统计量,表达式如下:

式中:μL(s)和分别表示以s为中心的图像子块的随机变量L的均值和随机变量Z的方差。在噪声图像中选定M个相同大小的图像子块,并且假定这些图像子块的亮度分布具有近似均匀与同质性。由于子块具有近似的同质性,所以图像子块的方差可以近似为0。又由于高斯噪声U的均值为0,则公式4可以转化为以下形式:

将式(5)、(6)联立,通过移项、对数变换得到γ的参数估计表达式:

为了增加参数估计的鲁棒性,将提取的全部图像子块中的可能的子块对进行累加,再求平均得到的参数估计值可以表示为

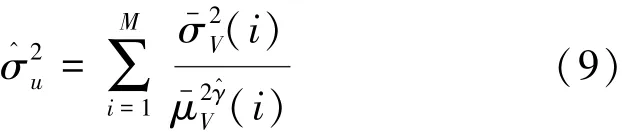
1.3 基于最大后验估计的变分模型
根据概率论的原理,对相关噪声的最优估计需要在已知观测数据的前提下,满足最大后验(maxi⁃mum a posteriori,MAP)估计准则[14]。由于退化图像的观测值已知,根据贝叶斯准则,只要得到不含噪声的条件概率模型和噪声的先验概率模型,就能够得到图像的后验概率模型。对式(2)进行移项就可以得到高斯噪声的数学模型,表达形式如下:

由于噪声Us满足均值为0,方差为的高斯噪声,根据在数理统计学原理,Z的似然函数可以表示为以下形式:
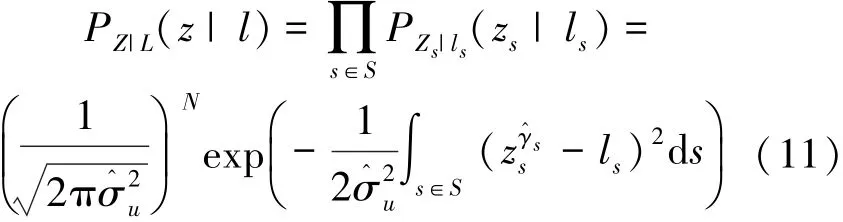
根据贝叶斯准则,Z的后验概率可以表示为
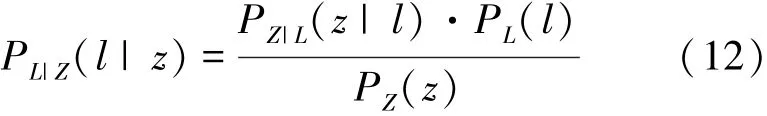
式中:PL(l)是L的先验概率,PZ(z)是Z的先验概率。V的先验概率是在L的样本空间内积分而得[14],即PL(l)=∫ω∈WPL(ω)dω,其中W是随机场L的样本空间。由于Z的概率分布不随L的取值不同而改变,所以可以将PZ(z)作为常数C来处理。L在样本空间上的概率分布满足马尔科夫随机场属性,因此L的先验概率需要满足如下表达式[14]:

式中:r是一个归一化常数。将式(11)、(13)代入式(12)中得到L的后验概率表达式:


式中:l就是L的最大后验估计。积分符号中的马尔可夫项和贝叶斯项都具有平方的表示形式,因此具有严格凸函数的性质,存在全局唯一的解l^是最大后验概率达到最大。
1.4 梯度法求解变分模型的最优解
因为抑制相关噪声的变分模型具有严格的凸函数性质,所以可以采用梯度法[15]求解变分模型的最优解,即不含相关噪声的恢复图像。采用相关噪声的迭代步骤可以表示为

式中:k表示迭代次数,λ是k次迭代对应的最优迭代步长,h(k)s是s点对应的梯度。根据欧拉-拉格朗日方程[16]可知,变分模型的梯度可以表示为

令变分模型为F[l],根据精确线过程[17],梯度法的最优迭代步长可以表示为
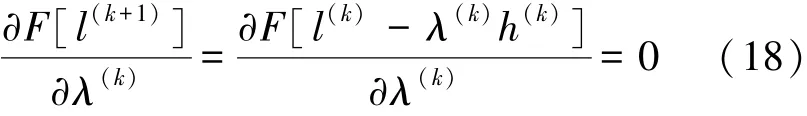
将式(17)代入式(18)中,通过图像的复制边界方法以及格林公式[18],推导出变分模型的最优迭代步长可以表示为

得到最优迭代步长后,将步长和梯度向量代入式(16)中就能够得到本次迭代对应的最优解。
本文算法的步骤可以归纳为如下4条:
1)通过基于图像子块的参数估计方法,估计噪声模型中的未知参数。
2)根据参数的估计值构造变分模型,设置变分模型的初始值。
3)将噪声的估计值代入式(17)、(19)中得到本次迭代的最优步长以及梯度向量,计算下一次迭代的初始值。
4)判断得到的最优解是否满足收敛条件,如果满足收敛条件,则该次迭代的解为最终的恢复图像;如果不满足收敛条件,则重复步骤3)直到满足收敛条件为止。
2 图像恢复结果与数据分析
本文的硬件平台是Pentium Dual⁃Core 2.70GHz双核处理器,2.00GB内存,仿真环境是Microsoft Visual Studio 2008,采用C++语言进行编程。实验部分采用标准的数字图像Lena作为输入,为Lena加入数学模型为式(1)形式的相关噪声得到退化图像。从2个方面说明了变分模型的有效性:首先,选取多组参数对退化图像进行恢复,得到对应的峰值信噪比(peak signal noise ration,PSNR),从而验证了只有在较为准确的参数的情况下得到的PSNR最大,从而论证了模型的有效性;其次,从主、客观两方面分析和比较各算法消除噪声的能力,验证了本文算法的有效性。
为标准数字图像Lena加入γ=0.7,σ=1的相关噪声得到的退化图像,其中图1(a)是不含相关噪声的原始图像,图1(b)是加入噪声后的退化图像。

图1 图像Lena和加入相关噪声的退化图像Fig.1 Image Lena and added noise degraded images
首先算法需要根据退化图像的不同局部子块获得相关噪声的参数估计,这里选取局部方差最小的50个子块,子块的尺寸为11×11的子块,子块在图像中的分布如图1(c)所示。再根据式(8)、(9)得到γ,σ参数估计值。为了验证参数估计的合理性,设置一些与真实值有一定偏差的参数,在此基础上得到各参数对应的PSNR。由于噪声模型中包含2个未知参数,所以需要固定一个参数,比较另一个参数对应的PSNR,从而验证参数估计算法的有效性。图2(a)是在σ=1的条件下,不同γ值得到的恢复图像对应的PSNR曲线。图2(b)是在γ=0.7的条件下,不同γ值得到的恢复图像对应的PSNR曲线。
从图2可以看出当γ和σ的值接近真实的参数值时,PSNR曲线到达峰值,此时恢复图像与原始图像的局部均值误差最小。当γ和σ距离真实的参数值较远时,PSNR越小,说明恢复图像与原始图像的差异越大。因此,本文提出的变分模型对于参数估计的精确度较为敏感,只有准确地参数估计才能得到去噪效果较高的恢复图像。从而可以间接地验证了模型的有效性。
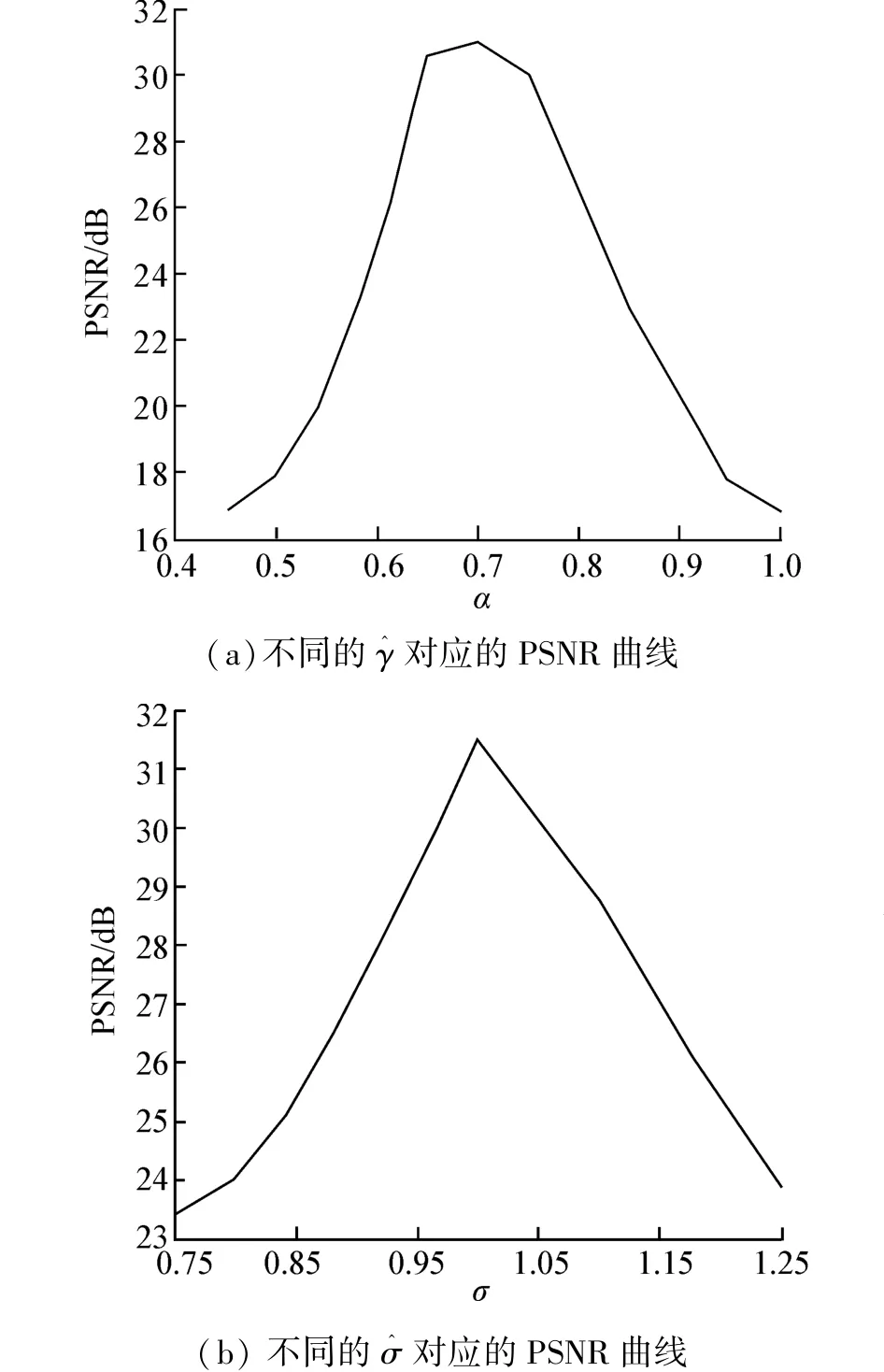
图2 不同参数条件下本文算法的PSNR曲线Fig.2 The PSNR curve of this algorithm under the condition of different parameters
图3 (a)~3(f)分别是通过LEE滤波器、SA⁃DCT算法、高阶模型[19]、PWLS算法、双边滤波+小波变换[20]方法、本文算法得到的恢复图像。图4(a)~4(h)是恢复图像的局部放大图像。


图3 各种去噪算法得到的恢复图像Fig.3 Images of various algorithms to restrain noise

图4 局部放大图Fig.4 Images of local enlarged
从图3和图4可以看出,LEE滤波器抑制噪声的能力最弱,图像整体的视觉效果受到噪声的影响较为严重;SA⁃DCT算法产生了模糊的效果,导致恢复图像的清晰度较差;高阶模型易出现过渡平滑现象,在噪声较严重的区域,恢复图像包含块状区域;PWLS算法的噪声抑制能力较好,但是恢复图像出现类似图像抖动的情况;双边滤波+小波变换方法恢复图像的局部区域产生细小的颗粒;与前几种算法相比,本文算法在噪声的抑制能力,细节保持能力,主观视觉效果等方面都有一定的改善。表1是各图像恢复算法得到的恢复图像的评价指标。
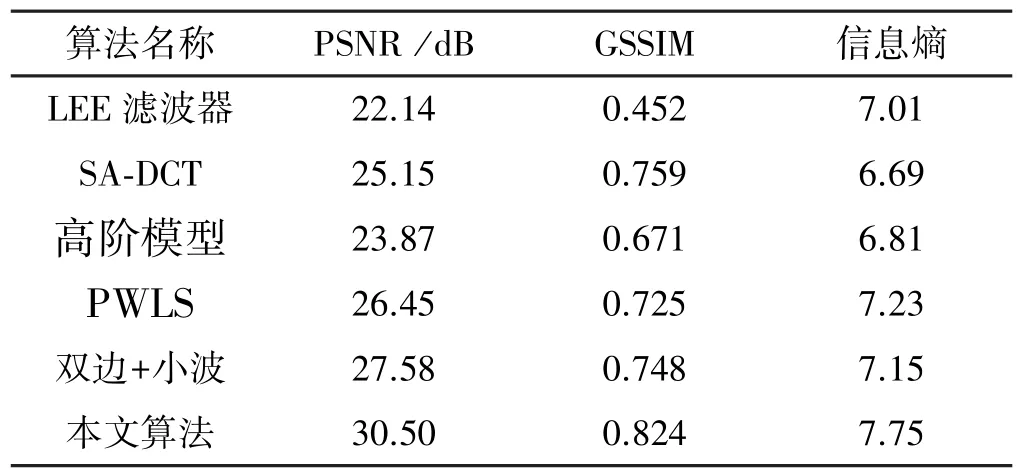
表1 各算法的客观评价指标Table 1 Objective evaluation of each algorithm
其中GSSIM[21]是衡量恢复图像与原始图像在结构方面的相似度系数,当GSSIM越高,则恢复图像与原始图像在结构上具有较强的相似度,反之亦然。信息熵决定了恢复图像的信息量的大小,当熵值越高,则恢复图像包含的信息量就越多,反之亦然。从表1可以看出,本文算法得到的恢复图像的PSNR、GSSIM,信息熵都比其他算法高。因此,与其他算法相比,本文算法得到的恢复图像具有较高噪声抑制能力,以及较强的细节保持能力。
图5(a)~5(c)的是通过数字相机采集到的含有相关噪声的水下图像,图5(d)~5(f)是通过本文算法得到的恢复图像。

图5 含有相关噪声的水下图像以及恢复图像Fig.5 The noise of underwater image and image restoration
从图5(a)~5(c)可知,水下的复杂环境产生的相关噪声引起了图像的对比度不均匀,物体的细节以及轮廓被噪声淹没等问题。本文算法能够有效地改善由相关噪声产生的视觉干扰,恢复图像的整体对比度,局部的细节特征都有了明显的提高和增强。
4 结束语
为了消除相关噪声对于水下图像的影响,本文构造了一个包含马尔可夫约束项和贝叶斯约束项的变分模型。通过梯度法得到该变分模型的最优解即为不含噪声的恢复图像。实验部分通过对包含相关噪声的标准图像以及水下图像进行恢复,验证了本文算法的有效性。
[1]张威,杨克成,范泛,等.基于模糊度量的激光水下图像复原的盲去卷积方法[J].光学与光电技术,2011,9(2):27⁃32.ZHANG Wei,YANG Kecheng,FAN fan,et al.Blind de⁃convolution approach based on blur metric method for laser underwater image restoration[J].Optics and Optoelectronic Technology,2011,9(2):27⁃32.
[2]昌彦君,谢志远,彭复员,等.散斑噪声污染的激光水下图像滤波算法[J].红外与激光工程,2002,31(4):318⁃321.CHANG Yanjun,XIE Zhiyuan,PENG Fuyuan,et al.Filte⁃ring algorithm on underwater laser image stained by speckle noise[J].Infrared and Laser Engineering,2002,31(4):318⁃321.
[3]BUADES A,COLL B,MOREL J M.A review of image de⁃noising algorithms with a new one[J].SIAM Journal on Mul⁃tiscale Modeling and Simulation,2006,4(2):490⁃530.
[4]WANG Xin.Wrap⁃around effect removal finite ridgelet trans⁃form for multiscale image denoising[J].Pattern Recogni⁃tion,2010,43(11):3963⁃3968.
[5]ZHANG Ming,GUNTURK B K.Multiresolution bilateral fil⁃tering for image denoising[J].IEEE Transactions on Image Processing,2008,17(12):2324⁃2333.
[6]HAN C,GUO H,WANG C,et al.A novel method to re⁃duce speckle in SAR images[J].International Journal of Remote Sensing,2002,23(23):5095⁃5101.
[7]REPETTI A,CHOUZENOUX E,PESQUET J C.A penal⁃ized weighted least squares approach for restoring data cor⁃rupted with signal⁃dependent noise[C]//Proceedings of 20th European Signal Processing Conference.Bucarest,2012,1553⁃1557.
[8]KOFIDIS E,THEODORIDIS S,KOTROPOULOS C,et al.Nonlinear adaptive filter for speckle suppression in ultrasonic images[J].Signal Processing,1996,52(3):357⁃372.
[9]FOI A,KATKOVNIK V,EGIAZARIAN K.Pointwise shape⁃adaptive DCT for high⁃quality denoising and de⁃blocking of grayscale and color images[J].IEEE Transac⁃tions on Image Processing,2007,16(5):1395⁃1411.
[10]BUADES A,COLL B,MOREL J M.A review of image de⁃noising algorithms,with a new one[J].SIAM Journal on Multiscale Modeling and Simulation,2006,4(2):490⁃530.
[11]AIAZZI B,ALPARONE L,BARONTI S,et al.Unsuper⁃vised estimation of signal⁃dependent CCD camera noise[J].EURASIP J Advances in Signal Processing,2012,2012(1):231⁃254.
[12]黄世奇,刘代志.SAR图像斑点噪声抑制方法与应用研究[J].测绘学报,2006,35(3):245⁃250.HUAGN Shiqi,LIU Daizhi.Research on method and appli⁃cation of speckle noise reduction of SAR image[J].Acta Geodaetica et Cartographica Sinica,2006,35(3):245⁃250.
[13]AIAZZI B,ALPARONE L,BARONTI S.A robust methodfor parameter estimation of signal⁃dependent noise models in digital Images[C]//1997 13th International Conference on Digital Signal Processing Proceedings.Santorini,1997,601⁃604.
[14]熊福松,王士同.基于高斯马尔可夫随机场的MAP估计在高斯噪声滤波中的应用[J].计算机应用,2006,26(10):2362⁃2365.XIONG Fusong,WANG Shitong.Application of MAP esti⁃mation based on Gaussian Markov random field in Gaussian noise filter[J].Computer Applications,2006,26(10):2362⁃2365.
[15]BOYD P,VANDENBERGHE L.Convex optimization[M].New York:Cambridge University Press,2004:87⁃95.
[16]AUBERT G,VESE L.A variational method in image re⁃covery[J].SIAM Journal of Numerical Analysis,1997,34(5):1948⁃1979.
[17]DAI Y H,YUAN Y.A nonlinear conjugate gradient meth⁃ od with a strong global convergence property[J].SIAM Journal of Optimization,1999,10(1):177⁃182.
[18]KIMMEL R,ELAD M,SHAKED D,et al.A variational framework for retinex[J].International Journal of Comput⁃er Vision,2003,52(1):7⁃23.
[19]MASO D G,FONSECA I,LEONI G,et al.A higher order model for image restoration:The one⁃dimensional case[J].SIAM Journal on Mathematical Analysis,2009,40(6):2351⁃2391.
[20]LEE J W,PARK R H,CHANG S.Noise reduction and a⁃daptive contrast enhancement for local tone mapping[J].IEEE Transactions on Consumer Electronics,2012,58(2):578⁃586.
[21]杨春玲,陈冠豪,谢胜利.基于梯度信息的图像质量评判方法的研究[J].电子学报,2007,35(7):1313⁃1317.YANG Chunling,CHEN Guanhao,XIE Shengli.Gradient information based image quality accessment[J].Acta Elec⁃tronica Sinica,2007,35(7):1313⁃1317.
Underwater image restoration algorithm to restrain correlated noise
XIAO Yihan1,PANG Yongjie2,ZHAO Lanfei1
(1.College of Information and Communication Engineering,Harbin Engineering University,Harbin 150001,China;2.Science and Technology on Underwater Vehicle Laboratory,Harbin Engineering University,Harbin 150001,China)
The traditional algorithm cannot get rid of the influence of correlated noise on underwater images.In view of this,this paper proposes a restoration algorithm to restrain the correlated noises of underwater images by establis⁃hing a variational model based on the theory of maximum a posteriori estimation that represents convex property.In the variational model,the probability distribution of noise is guaranteed via the item of Bayesian restraint.Mean⁃while the property of spatial continuity is satisfied via the Markov constraint.The gradient method is employed to ob⁃tain the optimal solution of the variational model,i.e.the restoration image without correlated noise.Experimental results show the correlated noise is eliminated by the proposed algorithm effectively;the restoration images present an excellent visual effect.
underwater image;correlated noise;variational model;gradient method
10.3969/j.issn.1006⁃7043.201404045
TP391.41
:A
:1006⁃7043(2015)06⁃0841⁃06
http://www.cnki.net/kcms/doi/10.3969/j.issn.1006⁃7043..html
2014⁃04⁃14.网络出版时间:2015⁃05⁃24.
国家自然科学基金资助项目(51179035/51279221);中央高校基本科研业务费专项资金资助项目(HEUCF140811).
肖易寒(1980⁃),女,讲师,博士;庞永杰(1955⁃),男,教授,博士生导师.
肖易寒,E⁃mail:yihan9999@sohu.com.

