具有撤销功能的基于身份的签密方案

刘振华，俎龙辉，李娟娟

（1.西安电子科技大学数学与统计学院，陕西西安710071；2.桂林电子科技大学广西信息科学实验中心，广西桂林541004）

具有撤销功能的基于身份的签密方案

刘振华1，2，俎龙辉1，李娟娟1

（1.西安电子科技大学数学与统计学院，陕西西安710071；2.桂林电子科技大学广西信息科学实验中心，广西桂林541004）

为了有效解决签密系统中撤销用户的问题，提出了具有撤销功能的基于身份的签密方案。方案将主密钥随机分布在初始密钥和更新密钥中，再随机生成签密密钥，从而不仅能有效撤销用户，而且能抵抗密钥泄露攻击。在标准模型下，证明了该方案基于DBDH问题假设，具有不可区分性；基于CDH问题假设，具有不可伪造性。同时，任何第三方在不访问明文的情况下，均可验证签密密文。

签密；密钥泄露；撤销；可证明安全；公开可验证

签密是在一个操作中既签名又加密，有效获得数据机密性和不可否认性的一种密码体制。签密方案具有更短的密文和更小的计算开销的优点。1997年，Zheng［1］首次提出签密概念。

当使用密码方案时，用户密钥丢失或泄露在所难免。在公钥加密系统中，一种撤销是通过文献［2］的技术实现证书撤销。在身份基加密系统中，Boneh等［3］指出要撤销某个用户，私钥生成中心停止为其发布更新密钥，并为其他用户产生更新密钥，这使得私钥生成中心工作量和用户数量成线性关系。之后Boldyreva等［4］提出利用二叉树结构实现高效撤销用户的方案，使得私钥生成中心更新次数仅为用户数量的对数次。然而，安全性证明仅在选择身份模型下实现的。在Boldyreva等的基础上，Libert和Vergnaud［5］提出了完全身份下的解决方案。Seo等将撤销功能推广到分级加密情形［6］，并提出能够抵抗密钥泄露攻击的加密方案［7］。锁琰等［8］提出一种基于密钥隔离的分布式群签名方案，但是需要分布式协助器帮助群成员完成密钥更新。另外，Tsai T.T.等［9］提出一个安全的具有可撤销功能的基于身份签名方案，并在标准模型下给出安全证明。

对基于身份的签密方案，具有撤销功能同样十分重要。2012年，Wu T.Y.等［10］首次给出了可撤销的基于身份的签密（revocable identity based signcryp⁃tion，RIBSC）的形式化定义与安全模型，并提出具体的方案。然而，该方案是在随机预言机模型下可证明安全的，在实际应用中却存在一定的安全隐患，并且在密钥生成过程中不具有随机性。

1 RIBSC形式化定义与安全模型

1.1 形式化定义

为了有效撤销用户，抵抗密钥泄露攻击，本文在文献［10］的RIBSC形式化定义中增加密钥生成算法和撤销算法，安全模型中增加了密钥询问，同时增加了有关密钥询问的限制条件。

可撤销的基于身份签密方案，包含以下算法：

1）Setup：输入安全参数k和时间T。返回系统的公共参数mpk和主私钥msk。

2）Initial Key extract：输入主私钥msk，身份ID。返回初始密钥skID。

3）Key update：输入主私钥msk，身份ID和时间T，撤销列表RL。若ID∉RL。返回身份ID在时间T的更新密钥kuT。反之，身份ID已经被撤销，返回⊥。

4）（Un）Signcryption Key generate：输入身份ID在时间T的初始密钥skID，更新密钥kuT。返回（解）签密密钥dkID，T或⊥（当ID∈RL时）。

5）Signcrypt：输入消息M，时间T，发送者身份IDA，接收者身份IDB。返回密文CT。

6）Unsigncrypt：输入密文CT，时间T，发送者身份IDA，接收者身份IDB。返回解签密密钥dkID，T和消息M'或⊥（当CT是无效密文时）。

7）Revoke：输入要撤销的身份ID和时间T，撤销列表RL。返回在时间T更新后的撤销列表RL。

1.2 安全模型

定义1 不可区分性（IND⁃CCA2）对于一个可撤销的基于身份的签密方案，如果不存在任何概率多项式数量级界的敌手A，可以以一个不可忽略的优势在以下的游戏中获胜，那么该方案具有适应性选择密文攻击下不可区分性。

Setup：挑战者B执行Setup算法，获得系统公共参数mpk和主私钥msk。将mpk发送给敌手A，自己保存msk。

第1阶段 敌手A执行适应性的多项式数量级界的以下询问：

1）Initial Key extract询问：A选择身份ID。B计算初始密钥skID，发给A。

2）Key update询问：A选择身份ID和时间T。B计算未撤销用户的更新密钥kuT，发给A。反之，若用户已经被撤销，返回⊥。

3）（Un）Signcryption Key generate询问：A选择用户的初始密钥skID，更新密钥kuT。B计算未撤销用户的（解）签密密钥dkID，T，发给A。

4）Signcrypt询问：A选择消息M，时间T，发送者IDA，接收者IDB。B计算密文CT，发给A。

5）Unsigncrypt询问：A选择密文CT，时间T，发送者IDA，接收者IDB。B计算消息M'，发给A。

挑战阶段 由A决定第1阶段何时结束。当结束后选择等长的消息，时间T∗，挑战的发送者身份，接收者身份发送给B。其中不能在第1阶段出现过。B随机选取γ∈{0，1}，运行Signcrypt算法，将密文CT∗，发给敌手A。

第2阶段 在A接收到B给的密文CT∗后，仍可以进行与第1阶段相似的多项式数量级界的询问，但是要满足一定的条件。

猜测 最后，A输出γ'，若γ＝γ'，敌手获胜。

定义2 不可伪造性（EUF⁃CMA）对于一个可撤销的签密方案，如果不存在任何概率多项式数量级界的敌手A，可以以一个不可忽略的优势在以下的游戏中获胜，那么该方案具有适应性选择消息攻击下存在性不可伪造性。

Setup：与IND⁃CCA2游戏中初始化过程相似。

第1阶段 敌手A执行与IND⁃CCA2游戏定义中相似的多项式数量级界的询问。

伪造阶段 敌手A输出对于挑战（m∗，T∗，ID∗A，ID∗B）的一个新的密文CT∗。当下列条件满足时，称敌手在该游戏中获胜。

①伪造的CT∗是对一个合法密文。

1.3 困难假设

定义3 DBDH问题令G，GT是大素数p阶循环群，g是群G的生成元，给定（g，ga，gb，gc）∈G4和T∈GT其中a，b，c∈Zp∗未知。G上的DBDH问题是判断是否有T＝e（g，g）abc。若任意概率多项式时间算法A解决DBDH问题的优势可忽略，则称群G上的DBDH困难问题假设成立。

定义4 CDH问题令G是大素数p阶循环群，g是该群的生成元，给定（g，ga，gb）∈G3，其中a，b∈未知。G上的CDH问题是计算gab∈G。若任意概率多项式时间算法A解决CDH问题优势可忽略，则群G上的CDH困难问题假设成立。

2 新的RIBSC具体构造

1）Setup 阶为素数p的乘法循环群G、GT，大小由安全参数k决定，g是群G的生成元，双线性对映射e：G×G→GT，随机选取，g2、h1、h2、h3、u'、u″、v'、v″、m'、ui、vi、mi←G，并计算g1＝gα、。向量U＝(ui)、V＝(vi)、M＝(mi)，长度分别为nu、nu、l。4个哈希函数H1：GT×{0，1}l，。输出mpk＝（G，GT，e＾，Hi，hj，g，g1，g2，u'，u″，v'，v″，U，V，M）msk＝（，其中i＝1，2，3，4，j＝1，2，3。nu为身份和时间的比特串长度。nm为消息比特串长度。

2）initial key extract 输入主私钥msk，身份ID。随机选取，使得ID[ i]表示ID的第i比特。是使得ID[ i]＝1索引i的集合。

初始私钥为

3）key update 输入主私钥msk，身份ID，时间T。对于时间T内的任意身份，若ID∉RL，随机选取，并计算，T[ i]表示T的第i比特，定义是使得T[ i]＝1的索引i的集合。更新密钥为

4）（Un）signcryption key generate 输入（ID，T）的初始密钥skID，更新密钥kuT。随机选取r1，，计算：

所以（解）签密密钥为

5）signcrypt 发送者以身份IDA和时间T执行以上2）、3）、4）算法获得签密密钥dkIDA，T。随机选取其中lτ为整数，对消息m计算：

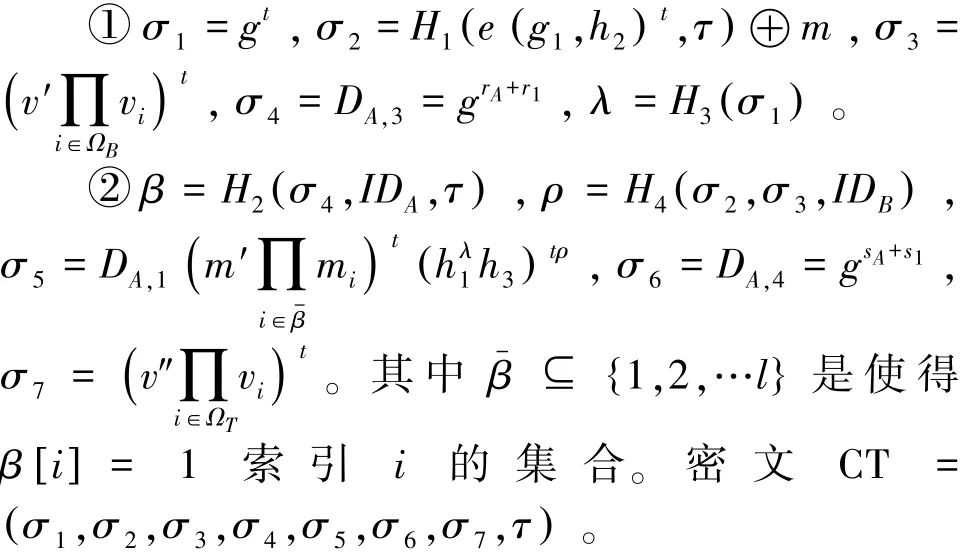
6）unsigncrypt 当IDB收到密文CT后：

①计算λ＝H3(σ1)，β＝H2(σ4，IDA，τ)，ρ＝H4(σ2，σ3，IDB，)。

②验证密文CT是否满足等式：

若（1）不成立，则CT是无效的密文，输出⊥。若等式（1）成立，则

a）计算IDB在时间T的解签密密钥

7）revoke 输入时间T和要撤销的身份ID，撤销列表RL。返回更新后的撤销列表RL。

3 安全性证明

定理1 （IND⁃RIBSC⁃CCA2）如果对于任何敌手只允许进行qc次初始密钥询问，qg次更新密钥询问，qj次签密密钥询问，qs次签密询问，qus次解签密询问，在概率多项式时间t内，最多具有ε的优势攻破所提出的方案的安全性，那么存在概率多项式时间t'的算法以ε'的优势解决DBDH问题：

Setup 模拟器B令lu＝2（qc+qg+qj）。因为在密钥提取询问终止的情况下，签密和解签密也不会终止，所以qs、qus是无限制条件的。B随机选取整数ku，0≤ku≤nu。假设lunu+1()＜p，随机选取x'，x″，xi←Zlu，y'，y″，yi←Zp，2个向量X＝（xi），Y＝（yi）长度均为nu。ID和T的函数：

为nu，nm。计算：

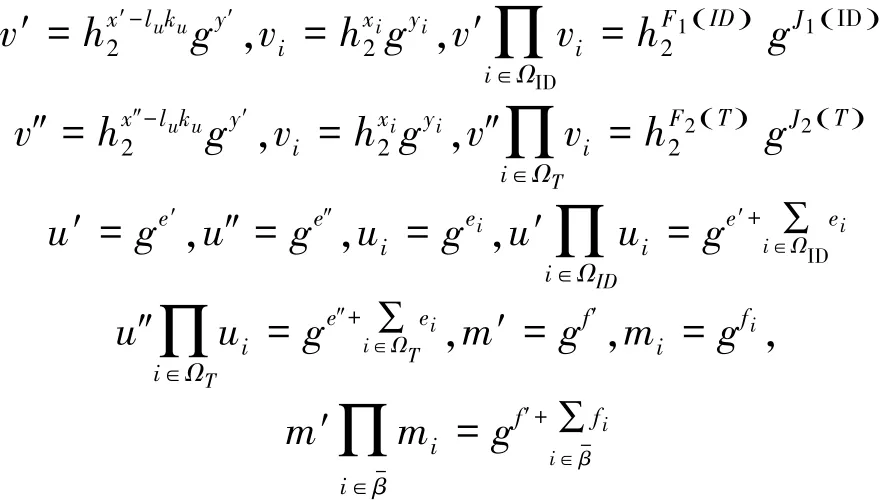
第1阶段

1）initial key extract询问：由于B不知道主密钥ha2，A以身份ID询问B时，随机选取r←Z∗p，gθ，hθ←G。按内外敌手如下计算：

①外部敌手时，若F1(ID)＝0( modp)，则输出⊥。

②内部敌手时，计算skID＝(skID，1，skID，2，skID，3)＝

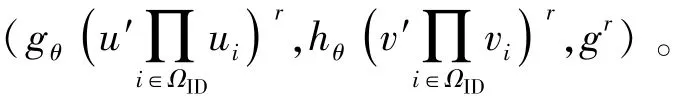
2）key update询问：当A以（ID，T）询问B时，若ID∉RL，B根据上述选定的gθ、hθ，计算，随机选取，如下计算：

①外部敌手时，计算kuT＝（kuT，1，kuT，2，kuT，3）＝

②内部敌手时，若F2T()＝0 modp()，则输出⊥。

否则，计算kuT＝（kuT，1，kuT，2，kuT，3）。

其中，s'＝s-a／F2T()。

3）（Un）signcryption key generate询问：当A以（ID，T）的初始密钥skID，更新密钥kuT向B询问时，B运行此算法，获得（解）签密密钥dkID，T。

4）signcrypt询问：当A以(m，T，IDA，IDB)向B询问时，B随机选取，τ←{0，1}lτ，lτ为整数。

①计算σ1＝gt，σ2＝H1(e( g1，h2)t，τ)⊕m，

5）unsigncrypt询问：A以(CT，T，IDA，IDB)向 B进行询问时，B首先验证等式（1）是否成立，若不成立，则输出⊥。否则，按内外敌手如下计算：

①外部敌手时，若F1IDB()≠0 modp()，运行Unsigncrypt算法恢复出明文。

②内部敌手时，若F2T()≠0 modp()，运行Un⁃signcrypt算法恢复出明文。

否则，当F1IDB()＝0 modp()，F2T()＝0 modp()时，计算：

m＝σ2⊕H1(e( Δ∗，h2)，τ)＝σ2⊕H1(e( g1，h2)t，τ)

挑战阶段。

计算

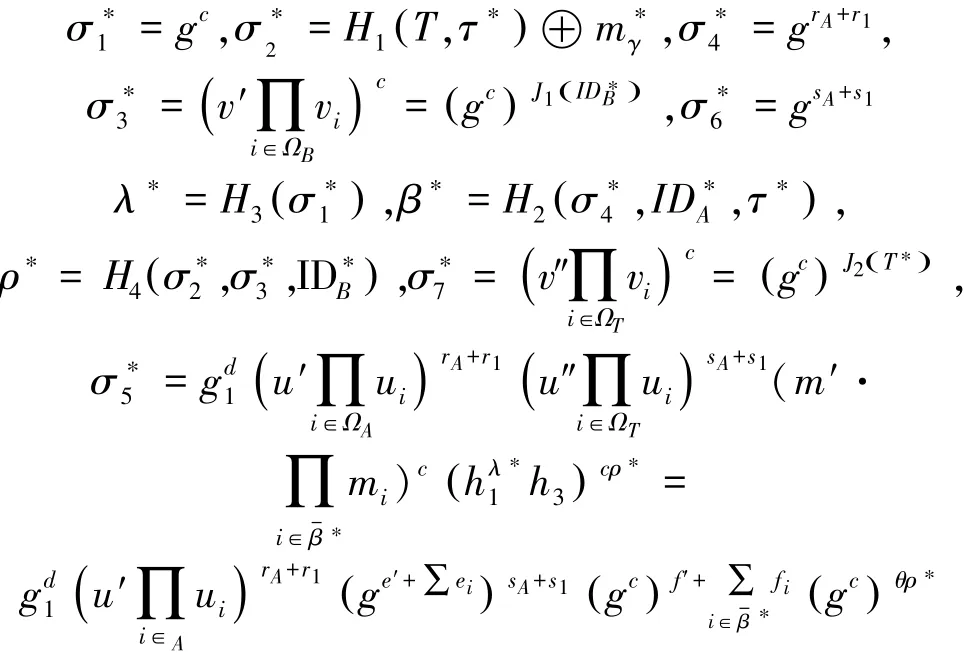
第2阶段 敌手A可以进行与第1阶段相似的询问，但是要满足定义1中的限制条件。

猜测A 输出对γ的猜测γ'，若γ'＝γ，则B输出1，意味着T＝e g，g()abc。否则输出0。

运用类似文献［9，11］的方法，B作为敌手A的挑战者，通过调用A解决DBDH困难问题的优势为

定理2 （EUF⁃RIBSC⁃CMA）如果对于任何敌手只允许进行qc次初始密钥询问，qg次更新密钥询问，qj次签密密钥询问，qs次签密询问，qus次解签密询问，在概率多项式时间t内最多具有ε的优势攻破所提方案的安全性，那么存在概率多项式时间t'的算法B以ε'的优势解决CDH问题：

证明 可参照定理1的证明得证。

4 效率分析与公开可验证性

4.1 效率分析

表1列出了本文方案与文献［10⁃11］方案计算效率和安全性比较。文献［10］中的方案是在随机预言机模型下可证明安全的。虽然具有高效率，但是不能保证方案的实际安全性。与文献［11］中的方案相比，本文方案签密运算多1个指数运算，解签密运算多2个双线性对运算，但本文方案具有撤销功能。因此，本文方案增加了计算量，但达到了更高的安全性。表中+1()Tp表示签密算法中的双线性对e( g1，h2)t运算的次数，Te表示一次指数运算。

表1 计算效率与安全性比较Table 1 Comparison of computation and security

4.2 公开可验证性

在如今开放网络上的通信、电子商务、电子政务等实际应用中签密文的公开验证是必不可少的。在解签密验证过程中，对于所有接收到密文CT的合法用户来说无需解密就可以直接验证方程（1）是否成立。因为由mpk可以得到（g，g1，g2，u'，u″，m'， U，M，h1，h3），由CT可以得到(σ1，σ4，σ5，σ6)和(λ，β，ρ)。因此方案的签名满足公开可验证性。

5 结论

本文改进了文献［10］中RIBSC的形式化定义与安全模型，并基于Selvi［11］的签密方案，构造出一种可以有效抵抗密钥泄露攻击的新RIBSC方案。在标准模型下，证明了新方案具有IND⁃CCA2和EUF⁃CMA安全性。此外，所提方案又能保证在不访问明文的情况下，任何第三方都可以对密文进行公开验证，达到了签密在电子商务、电子政务等实际应用中公开验证的要求。然而，所提方案计算复杂度与用户数量成线性关系，下一步研究工作重点是对其进行效率提高。

［1］ZHENG Y L.Digital signcryption or how to achieve cost（sig⁃nature and encryption）＜＜cost（signature）+cost（encryp⁃tion）［C］／／Advances inCryptology—CRYPTO'97.Berlin：Springer，1997：165⁃179.

［2］GOYAL V.Certificate revocation using fine grained certifi⁃cate space partitioning［C］／／Financia Cryptography and Da⁃ta Security.Berlin：Springer，2007：247⁃259.

［3］BONEH D，FRANKLIN M.Identity⁃based encryption from the weil pairing［C］／／Advances in Cryptology⁃CRYPTO 2001.Berlin：Springer，2001：213⁃229.

［4］BOLDREVA A，GOYAL V，KUMER V.Identity⁃based en⁃cryption with efficient revocation［C］／／Proceedings of the 15th ACM Conference on Computer and Communications Se⁃curity.Berlin：Springer，2008：417⁃426.

［5］LIBERT B，VERGNAUD D.Adaptive⁃ID secure revocable identity⁃based encryption［C］／／Topics in Cryptology⁃CT⁃RSA2009.Berlin：Springer，2009：1⁃15.

［6］SEO J H，EMURA K.Efficient delegation of keygeneration and revocation functionalities in identity⁃based encryption［C］／／Topics in Cryptology-CTRSA 2013.Berlin：Spring⁃er，2013：343⁃358.

［7］SEO J H，EMURA K.Revocable identity⁃based encryption revisited：security model and construction［C］／／Public⁃Key Cryptography⁃PKG2013.Berlin：Springer，2013：216⁃234.

［8］锁琰，李晓辉，徐小岩，等.一种安全的分布式群签名方案［J］.哈尔滨工程大学学报，2011，32（12）：1594⁃1623.SUO Yan，LI Xiaohui，XU Xiaoyan，et al.A secure distribu⁃ted group signature scheme［J］.Journal of Harbin Engineer⁃ing University，2011，32（12）：1594⁃1623.

［9］TSAI T T，TSENG Y M，WU T Y.Provably secure revoca⁃ble ID⁃based signature in the standard model［J］.Security and Communication Networks，2013，6（6）：669⁃796.

［10］WU T Y，TSAI T T，TSENG Y M.A revocable ID⁃based signcryption scheme［J］.Information Hiding and Multi⁃media Signal Processing，2012，3（3）：240⁃251.

［11］SELVI S S D，VIVEK S S，VINAYAGAMURTHY D，et al.ID based signcryption scheme in standard model［C］／／Provable Security.Berlin：Springer，2012：35⁃52.

Identity⁃based signcryption with the revocation function

LIU Zhenhua1，2，ZU Longhui1，LI Juanjuan1

（1.School of Mathematics and Statistics，Xidian University，Xi'an 710071，China；2.Guangxi Experiment Center of Information Sci⁃ence，Guilin University of Electronic Technology，Guilin 541004，China）

An identity⁃based signcryption scheme with revocation is proposed in order to solve the problem of revo⁃king users in the signcryption system.In this scheme，the master key is randomly distributed in the initial key and update key，which are used to generate the signcryption key randomly.Thus，the proposed scheme can revoke users effectively as well as resist key compromise attack.In the standard model，the scheme is proven to be indistinguish⁃able and unforgettable against adaptive chosen ciphertext attacks and adaptive chosen message attacks under deci⁃sional bilinear Diffie⁃Hellman assumption and computational Diffie⁃Hellman assumption，respectively.Furthermore，any third party can verify the ciphertext without accessing plaintext.

signcryption；key compromise；revocation；provable security；public ciphertext verifiability

10.3969／j.issn.1006⁃7043.201401033

TN 918.1

：A

：1006⁃7043（2015）02⁃0856⁃05

http：／／www.cnki.net／kcms／detail／23.1390.U.20150428.0928.015.html

2014⁃01⁃12.网络出版时间：2015⁃04⁃28.

国家自然科学基金资助项目（61472470，61100229）；陕西省自然科学基金资助项目（2014JM2⁃6091，2015JQ1007）；广西信息科学实验中心经费资助（20130201）.

刘振华（1978⁃），男，副教授，博士；俎龙辉（1987⁃），女，硕士研究生.

俎龙辉，E⁃mail：sdjnlonghui＠126.com.