用单叶双曲螺旋线光滑拼接两条异面直线

邱梦鸾，白根柱

（内蒙古民族大学数学学院，内蒙 古通辽 028043）

用单叶双曲螺旋线光滑拼接两条异面直线

邱梦鸾，白根柱

（内蒙古民族大学数学学院，内蒙 古通辽 028043）

讨论了两条异面直线可用单叶双曲螺旋线光滑拼接的条件，给出了具体实例，并用数学软件画出了拼接的效果图.

异面直线；单叶双曲螺旋线；光滑拼接

在计算机辅助几何设计中，曲线、曲面拼接就是将两个或两个以上的曲线、曲面用一个曲线、曲面光滑拼接起来.有关共面直线或轴线共面的管道之间光滑拼接技术的研究较多［1－9］，而关于异面直线或轴异面管道之间光滑拼接的研究结果并不多，文献［10］提出构造轴线与给定二异面圆管的轴分别共面的辅助圆柱，并利用二轴共面的吴文俊公式实现了给定圆管的分两段三次光滑拼接，文献［11］给出了两个轴线异面的圆管道存在三次拼接曲面的充要条件，并给出了当存在光滑拼接的三次曲面时，两个圆管道系数之间的关系，文献［12］利用螺旋线对两条异面直线进行光滑拼接，实现了利用广义圆柱螺旋管光滑拼接轴线异面的管道，文献［13］利用空间Bézier曲线对两条异面直线进行光滑拼接，实现了用广义圆柱管道光滑拼接轴线异面的管道，文献［14］分别以推广的Hartmann函数曲线和两个锥面的交线为过渡曲线，对两条异面直线进行了光滑拼接，实现了以此过渡曲线为轴线的管道光滑拼接两个轴异面的圆管道.本文主要讨论了用单叶双曲螺旋线实现两条异面直线之间的光滑拼接问题，为进一步研究两个轴异面管道之间的光滑拼接打基础.

1 基本理论

其中a，b，c，L都是正数．

在几何造型中，两曲线拼接时，有两种方法度量曲线间拼接的光滑度，一种是函数的可微性方法，把拼接参数曲线构造成在连接处具有直到n阶连续导矢，即n次连续可微，这类光滑度称之为Cn或n阶参数连续性；另一种称为几何连续性，即合成曲线在拼接点处满足不同于Cn的某一组约束条件，称为具有n阶几何连续性，简记为Gn．

定义2 若对任意的两个方向向量d1和d2的每一个分量为Cn连续，称d1和d2为Cn连续．

定义3 若空间曲线l0与两条空间异面直线l1、l2分别在拼接点处Cn连续，则称l0与l1、l2、Cn连续．

给定两条直线l1和l2分别为：

其中点M1（X1，Y1，Z1）在直线l1上，d1（A1，B1，C1）是 l1的方向向量，点 M2（X2，Y2，Z2）在直线l2上，d2（A2，B2，C2）是l2的方向向量．这两条空间直线异面的充要条件是：

定理1 能够与式（1）和式（2）在点M1（X1，Y1，Z1）和点M2（X2，Y2，Z2）处分别光滑拼接的单叶双曲螺旋线应满足的条件：

1）位置连续：C（β1）＝M1（X1，Y1，Z1），C（β2）＝M2（X2，Y2，Z2），即：

其中β1，β2分别为单叶双曲螺旋线在点M1（X1，Y1，Z1）和点M2（X2，Y2，Z2）处的转角，则单叶双曲螺旋线的参数方程为：

其中a，b，c，L为满足条件的任一正数．

为了保证C（β）与l1、l2达到切矢方向的连续，需满足d1＝ε·C′（β1），d2＝δ·C′（β2）其中ε，δ＞0，即得证条件式（2）．

综上，可知能够GC1光滑拼接两异面直线l1、l2的单叶双曲螺旋线的参数方程为：

其中a，b，c，L都是正数．

2 实例

例1 已知两条异面直线l1和l2，其参数方程分别为：

则能够光滑拼接两异面直线l1和l2的单叶双曲螺旋线的参数方程为：

例2 已知两条异面直线l3和l4，其参数方程分别为：

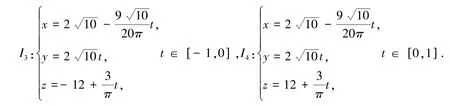
则能够光滑拼接两异面直线l3和l4的单叶双曲螺旋线的参数方程为：

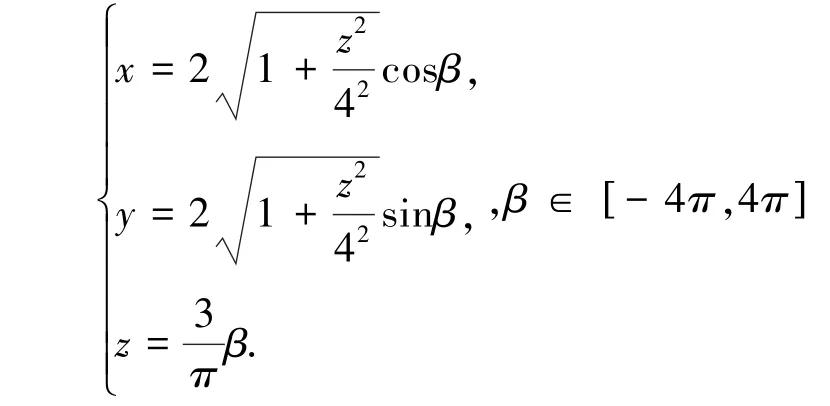
图1 用单叶双曲螺旋线光滑拼接异面直线l1和l2 Fig.1 Employing hyperbolic spiral of one sheet to smoothly blend two non－coplanar straight lines l1，l2

图2 用单叶双曲螺旋线光滑拼接异面直线l3，l4Fig.2 Employing hyperbolic spiral of one sheet to smoothly blend two non－coplanar straight lines l3，l4

3 结束语

在讨论用单叶双曲螺旋线光滑拼接给定的异面直线的过程中，讨论了以z轴为中心的螺旋线光滑拼接两个异面直线的问题.此方法可以推广到给定任意两个异面直线可用单叶双曲螺旋线光滑拼接的情形.另一方面，将进一步研究在轴线光滑拼接的前提下，两个轴异面管道的光滑拼接问题，这对于研究轴异面管道光滑拼接具有理论价值和实际应用价值.

［1］吴文俊，王定康.CAGD中的代数曲面拟合问题［J］.数学的实践与认识，1994（3）：26－31.

［2］朱汉东，金通光.过渡曲面的母线构造法［J］.工程图学学报，1998，19（3）：45－48.

［3］Hartmann E.Numerical implicitization for intersection and Gn－continuous blending of surface［J］.CAGD，1998，15：377－397.

［4］Wu T R，Zhou Y S.On blending of several quadratic algebraic surfaces［J］.CAGD，2000，17：759－766.

［5］Chen F L，Chen C S，Deng J S.Blending pipe surfaces with piecewise algebraic surfaces［J］.Chinese J Computers，2000，23（9）：911－916.

［6］Hartmann E.Gn－continuous connections between normal ringed surfaces［J］.CAGD，2001，18：751－770.

［7］Cheng J S.Blending quadric surfaces via a base curve method［C］／／Proceedings of ASCM03 World Scientific，2003：77－86.

［8］刘雪峰.环面构造管道拼接曲面的方法及其连续性［J］.中国科学技术大学学报，2004，34（1）：20－28.

［9］程进三，高小山.构造两个曲面的拼接曲面［J］.工程图学学报，2005（1）：39－44.

［10］雷娜，崔丽，伍铁如.两个轴异面的管道拼接［J］.吉林大学学报：理学版，2002，40（2）：138－140.

［11］白根柱.两个轴异面圆柱面的光滑拼接问题［D］.长春：吉林大学，2004.

［12］Han Wang，Gen－zhu Bai.Employing Generalized Cylindrical Helicoid Tube to smoothly Ble－nding Tubes whose Axes are Non－coplanar［J］.Ap⁃plied Mechanics and Materials，2013，380／384：1750－1754.

［13］Gen－zhu Bai，Han Wang，Zhao－jieYin.Employing Generalized Bezier Tube to smoothly Ble－nding Tubes whose Axes are Non－coplanar［J］.Ap⁃plied Mechanics and Materials，2014，513／517：2301－2306.

［14］BAI Gen－zhu，LIU Si－yu，WANG Han，et al.A novel method for smooth blending cylindrical surfaces whose axes are non－coplanar based on smooth blending axes［J］.Matericals Science and Information Technologies in Industry，2014，29：687－691.

责任编辑：时 凌

Smoothly Blending Two Non－coplanar Straight Lines Employing Hyperbolic Spiral of One Sheet

QIU Mengluan，BAI Genzhu
（College of Mathematics，Inner Mongolia University for Nationalities，Tongliao 028043，China）

We discuss the conditions of the smooth blending between two non－coplanar straight lines by the hyperbolic spiral of one sheet，cite specific examples and draw the splicing effect pictures using math⁃ematical software.

non－coplanar straight lines；hyperbolic spiral of one sheet；smooth blending

O187.1

A

1008－8423（2015）03－0256－04

10.13501／j.cnki.42－1569／n.2015.09.005

2015－05－23.

内蒙古民族大学科学研究基金项目（NMDGP1415）.

邱梦鸾（1990－），女，硕士生，主要从事计算机辅助几何设计的研究.