一种基于协方差矩阵行列式的频谱感知方法
刘昆,王志平
(1.国家海洋局南海工程勘察中心,广东 广州 510300; 2.中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
一种基于协方差矩阵行列式的频谱感知方法
刘昆1,王志平2
(1.国家海洋局南海工程勘察中心,广东 广州 510300; 2.中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
针对最大最小特征值检测法(Maximum-minimum Eigenvalues Based Detector,MMED)需要对协方差矩阵进行特征分解,计算复杂度较高的问题,提出了一种基于采样协方差矩阵行列式的频谱感知方法。该频谱感知方法利用了矩阵行列式的所有特征值,只需要计算采样协方差矩阵的行列式,即可得到接近或者稍优于MMED的感知结果。仿真分析结果表明,与MMED相比,所提出的频谱感知方法不仅计算复杂度低,而且具有更佳的感知性能。
认知无线电;频谱感知;协方差矩阵;矩阵行列式
0 引言
随着3G和LTE等无线通信业务的快速增长,大量的频谱资源以固定频谱资源分配方式被分配给了授权业务。这使得现有的频谱资源缺乏的现象变得越来越严重[1]。而固定分配方式的频谱利用率非常低,实测数据表明,现有业务的频谱使用率平均在5~15%之间。为解决频谱资源利用率低下的问题,工业界和学术界开始考虑利用动态频谱分配方式来进行频谱管理[2]。认知无线电(Cognitive Radio,CR)是近来提出来的能有效提高频谱资源利用率的技术,该技术是实现频谱资源动态分配的方案之一[3-5]。其中,频谱感知是认知无线电技术中的关键组成部分,它可以有效阻止采用CR技术的无线业务对在同一频段中的授权用户产生干扰。一般情况下,常见的认知无线电频谱感知有能量检测法[6,7]、循环平稳检测法[7]和匹配滤波器法[8,9]等。
除了以上3类常见的频谱感知方法,协方差矩阵特征值检测方法,例如最大最小特征值检测法(Maximum-minimum Eigenvalues Based Detector,MMED)是近几年提出的具有较好检测性能的一类感知方法[8-11]。MMED方法需要对接收信号的采样协方差矩阵进行特征分解来获得最大和最小特征值,因此该方法计算复杂度较高。针对上面提到的问题,提出了一种基于采样协方差矩阵行列式的频谱感知方法,所提出的方法只需要计算采样协方差矩阵的行列式,因此具有较低的计算复杂度。
1 系统模型
假设某个认知无线电系统中配备有M根接收天线,其中第i(i=1,2,…,M)根天线接端对接收到的基带信号经时域采样得到的第k点离散基带信号表示为xi(k)。另外,假设第i根天线的信号可以如下表示为:
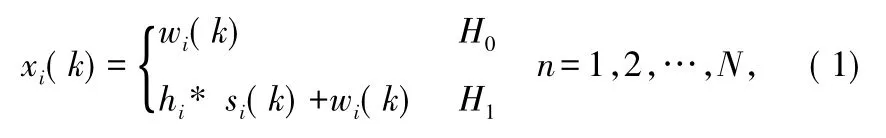
式中,hi表示第i根天线接收信道的信道增益,如果该信道是平坦非选择性慢衰落信道,则可以假设在感知采样周期内中该系数是恒定的,另外假设M根天线接收信道的衰落系数是独立同分布的。si(k)和wi(k)分别表示第i根天线在第k点采样所得的信号和噪声。H0代表没有授权信号的情况,H1代表有授权信号的情况。
2 频谱感知
2.1 最大最小特征值检测法
令x(k)=[x1(k)…xM(k)]T为在第k点采样时刻M根天线采样所得的M×1维向量。K点采样所得的采样协方差矩阵可以表示为:
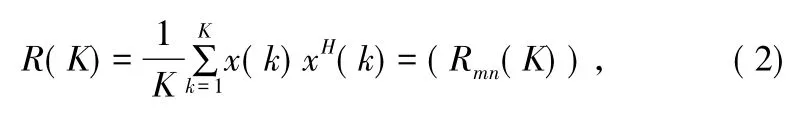
式中,Rmn(K)为R(K)的第m行、第n列的元素。则最大最小特征值检测法的检验统计量为:
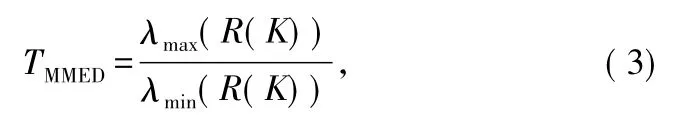
式中,λmax(·)和λmin(·)分别表示取矩阵的最大和最小特征值。
2.2 所提的频谱感知方法
矩阵的特征值计算的复杂度非常高,本文利用矩阵的行列式进行频谱感知,假设噪声功率已知,常用的能量检测法中经常假设已知,因此这个假设具有一定的合理性。噪声功率也可以通过静默期估计获得。所提出的频谱感知方法的检验统计量为:
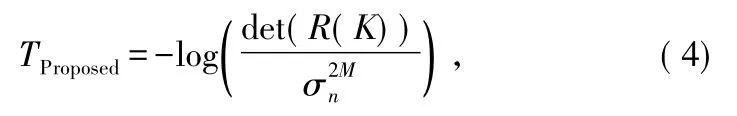
式中,det(·)表示取行列式操作。
众所周知,矩阵的行列式等于该矩阵所有特征值的乘积。所以所提出的方法利用了所有特征值。而MMED方法只利用了最大和最小2个特征值。考虑最大和最小2个特征值在所有特征值中对频谱感知的性能起着决定性的作用,因此所提方法在检测性能方面只能够接近或者稍微优于MMED。
在采集信号中不存在授权用户,即只有高斯白噪声信号的情况下,根据文献[12]可知,此时TProposed的概率密度函数与M个独立同分布的χ2分布的随机变量的乘积具有相同的分布。因此很容易通过计算机仿真获得。
3 仿真分析
下面比较研究所提方法与MMED法的频谱感知性能。假设设定M=4,K=100。首先比较在存在和不存在授权用户信号时,所提方法和MMED法的检验统计量的分布情况。假设信噪比为-5 dB。MMED法的检验统计量通过100 000次蒙特卡洛仿真获得的概率密度函数如图1所示。图1(a)为存在主用户情况,图1(b)为不存在主用户情况。
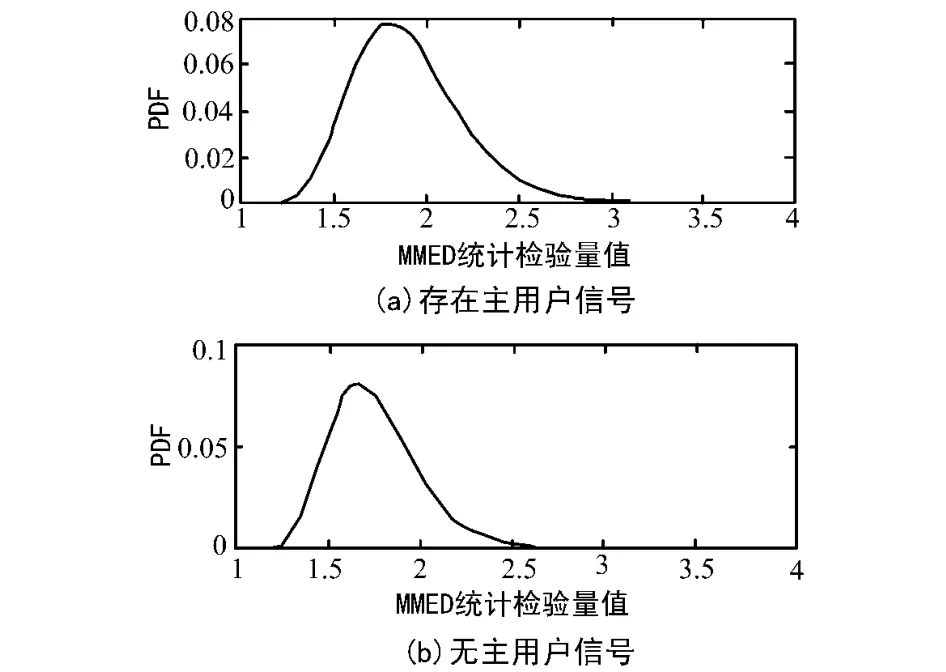
图1 MMED法检验统计量的概率密度函数
所提方法检验统计量的概率密度曲线(PDF)如图2所示。从图2可以看出所提方法的2条曲线重叠比例低于MMED法的曲线,因此所提方法能够获得更加高的检测性能。
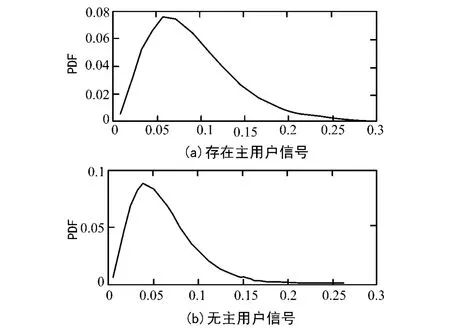
图2 所提方法检验统计量的概率密度函数
下面通过ROC(接收机操作特性曲线)来研究所提方法的检测性能,假设仿真参数如上面的实验不变,所提方法和MMED法的ROC曲线如图3所示。
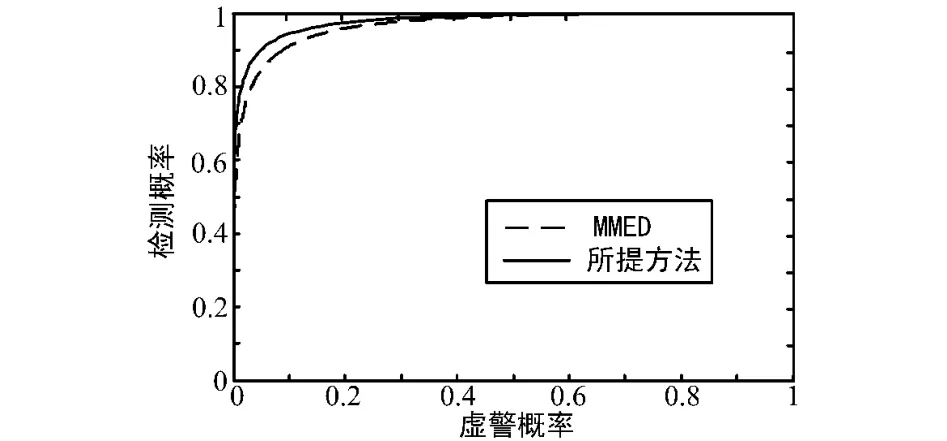
图3 所提方法和MMED法的ROC曲线
从图3可以看出,所提方法比MMED方法的检测性能略有提高。需要说明的是,尽管性能提高不是很大,但是所提方法具有更低的计算复杂度。
这里定量比较2种方法的计算量。由于硬件实现时乘法运算计算量远远大于加减运算,所以这里只考虑乘法运算次数众所周知,计算矩阵特征值的计算中乘法次数与矩阵维数的三次方(即M3)成正比。下面分析所提方法的计算量,从式(4)可知所提方法的计算量主要在于计算矩阵的行列式,首先把R(K)分块如下:

式中,a为标量,b为维数M-1的行向量,c为M-1维的列向量,D为M-1维的方阵。根据分块矩阵行列式计算公式可知:

通过上式可得M维的行列式运算降解为了M-1维运算。假设M维的行列式运算量为CM,上式中cb的乘法次数为(M-1)2。因此矩阵行列式的乘法次数有如下的递推公式:

式中,第2个等式当M较大时成立。考虑到C2=2,通过递推可得:

4 结束语
提出的基于采样协方差矩阵行列式的频谱感知方法,是对现有MMED方法的补充和完善,该方法克服了MMED方法需要进行特征分解从而计算量高的问题,有效降低了计算复杂度。通过仿真结果对比表明,提出的频谱感知方法相比MMED方法具有更低的计算量和较好的检测性能。
[1]Mitola J,III Mitre Corp,McLean V A.III M J.Cognitive Radio for Flexible Mobile Multimedia Communications[J].Mobile Networks and Applications,2001,6(5):435-441.
[2]LIN Wei,ZHANG Qin-yu.A Design of Energy Detector in Cognitive Radio under Noise Uncertainty[C]∥Communication Systems,2008.ICCS 2008.11th IEEE Singapore International Conference,2008:213-217.
[3]Kim S,Lee J,Wang H,et al.Sensing Performance of Energy Detector with Correlated Multiple Antennas[J].IEEE Signal Proc.Let.,2009,16(8):671-674.
[4]Chen H S,Gao W,Daut D G.Signature based Spectrum Sensing Algorithms for IEEE 802.22 WRAN[C]∥IEEE Int.Conf.Commun.,Glasgow,U.K,Jun,2007:6487-6492.
[5]Cabric D,Tkachenko A,Brodersen R W.Spectrum Sensing Measurements of Pilot,Energy,and Collaborative Detection[C]∥MILCOM,Washington,DC,2006:1-7.
[6]Sutton P D,Nolan K E,Doyle L E.Cyclostationary Signatures in Practical Cognitive Radio Applications[C]∥Selected Areas in Communications,2008:13-24.
[7]Miao Yang,JianpingAn,XiangyuanBu,etal.An Improved Eigenvalue-Based Algorithm for Cooperative Spectrum Sensing[C]∥Wireless Communications Networking and Mobile Computing(WiCOM),2010:1-4.
[8]Nadler B,Penna F,Garello R.Performance of Eigenvalue-Based Signal Detectors with Known and Unknown Noise Level.Communications(ICC)[C]∥2011 IEEE International Conference,2011:1-5.
[9]Zeng Y,Liang C.Spectrum-Sensing Algorithms for Cognitive Radio Based on Statistical Covariances[J].IEEE Trans.Veh.Technol,2009,58(4):1804-1815.
[10]Zeng Yonghong,Liang Ying-Chang.Covariance Based Signal Detections for Cognitive Radio[C]∥New Frontiers in Dynamic Spectrum Access Networks,2007.DySPAN 2007.2nd IEEE International Symposium,2007:202-207.
[11]Lindsay B G.On the Determinants of Moment Matrices[J].The Annals of Statistics,1989,17(2):711-721.
A Novel Spectrum-sensingMethod Based on Determinant of Covariance Matrix
LIU Kun1,WANG Zhi-ping2
(1.South China Sea Marine Engineering Surveying Center,Guangzhou Guangdong 510300,China; 2.The 54th Research Institute of CETC,Shijiazhuang Hebei 050081,China)
The maximum-minimum eigenvalues based detector(MMED)has high computational complexity due to its eigen-decomposition of covariance matrix.In the paper,a novel spectrum-sensing method based on the determinant of covariance matrix is proposed.Compared with the MMED,the proposed method has lower computational load.Numerical simulations show that the proposed method has better detection performance than the MMED does.
cognitive radio;spectrum-sensing;covariance matrix;matrix determinant
TN98
A
1003-3114(2015)05-53-3
10.3969/j.issn.1003-3114.2015.05.14
刘昆,王志平.一种基于协方差矩阵行列式的频谱感知方法[J].无线电通信技术,2015,41(5):53-55.
2015-06-02
刘昆(1978—),男,工程师,主要研究方向:通信与电子工程。王志平(1983—),男,工程师,主要研究方向:无线电监测技术。

