波束成形下DMIMO系统下行小区平均遍历容量分析

范超，崔磊

(1．中国人民解放军92117部队，北京 100072; 2．河海大学，江苏 南京 211100)

波束成形下DMIMO系统下行小区平均遍历容量分析

范超1，崔磊2

(1．中国人民解放军92117部队，北京 100072; 2．河海大学，江苏 南京 211100)

主要对波束成形下分布式MIMO系统下行小区平均遍历容量展开分析。首先建立了包含快衰落、阴影衰落和路径损耗的复合衰落信道模型。然后，在分布式基站功率受限条件下，推导各基站权重向量即最优波束;并基于ST-MRT传输策略，推导特定移动台位置条件下，小区下行点对点遍历容量表达式。最后，考虑移动台在小区内任意分布的特征，进一步推导出波束成形下小区平均遍历容量理论近似表达式。结果表明所推导的理论近似表达式可很好地反应系统的实际性能。

波束成形；分布式MIMO系统；遍历容量

0 引言

分布式MIMO系统(DMIMO)以其覆盖范围广和功率消耗低等特点逐渐成为研究的热点［1］。与传统集中式MIMO系统(CMIMO)相比，DMIMO系统不仅可以利用宏分集增益克服大尺度衰落的影响，还可以通过减小天线与用户之间的接入距离，减少小区覆盖区域内的盲点来提高系统覆盖特性［2，3］。研究表明DMIMO系统不论在提高系统容量、分集度，还是在降低中断概率、节省发送功率等方面都显示出CMIMO系统不可比拟的优势，我国已将DMIMO系统作为未来的网络架构。

以往对小区系统容量的研究大部分都是基于全向天线的，在通信过程中会对小区内其他用户和基站产生干扰，而基于智能天线的波束成形技术可以有效降低干扰。目前国内外对基于波束成形方案DMIMO系统小区基站侧多天线最优覆盖的研究较少。文献［1］研究了瑞利信道下，接收端已知信道状态信息(CSI)，发送端天线等功率发送相互独立的信号，获取信道遍历容量。文献［2］信道容量的获取是在接收端与发射端已知信道状态信息条件下，发送端采用注水定理对天线功率进行自适应分配得到。文献［3］和文献［4］分别讨论了上行链路中多用户系统总功率受限与单用户系统功率受限条件下系统的渐进容量。文献［5］分析了DMIMO系统下行链路单用户多小区的场景，其中分布式天线端口配置单根天线且功率受限，并从信息论的角度通过减小其他小区的干扰获得容量增益。文献［6］在DMIMO系统单小区内，通过平方距离准则优化天线位置，使得小区平均遍历容量理论下界达到最大。文献［7］在MISO系统中，单用户且每根天线功率受限条件下，通过简化半正定矩阵的方法，发送端获取最优加权向量。本文主要讨论在圆形小区DMIMO系统中，分布式天线端口功率受限条件下对小区系统容量进行推导分析。

1 系统模型

首先考虑将圆型小区作为传统蜂窝小区简化模型。如图1所示，假设小区半径为R。其中，N个基站(分布式天线端口)通过电缆或光纤与中心处理单元(MPU)连接，每个基站配置不同数目的天线，即DAUi配置Mi根天线形成天线阵列，(ri，βi)(i= 1，2，…，N)表示DAUi在小区内分布坐标。同时，移动台(MS)任意分布在小区内，且MS配置1根天线，(ρ，θ)表示MS在小区内坐标。

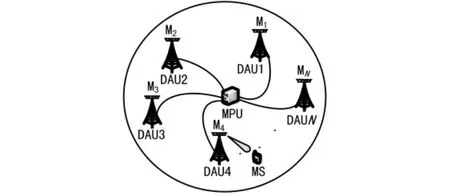
图1 圆形小区分布式MIMIO系统示意图

信道建模方面，假设为噪声受限的DMIMO系统，且整个信道是平坦衰落和准静态的。在系统下行链路中，选择采用传输(ST)方案，接收端的信号可表示为:

式中，y是接收信号;xi是DAUi发送信号向量;在实际的DMIMO系统中各个分布式基站之间是相互独立的。假设各个分布式基站功率受限，则有， Pi表示DAUi的发送功率。hi表示DAUi与某一特定位置MS之间的Mi×1复合衰落信道矩阵。n是零均值复高斯白噪声向量，且有E(n nH)=1。

由于小区内各个基站是分散放置的，在信道建模时同时考虑了小尺度和大尺度2种衰落。则MS与DAUi之间的复合衰落信道建模为:

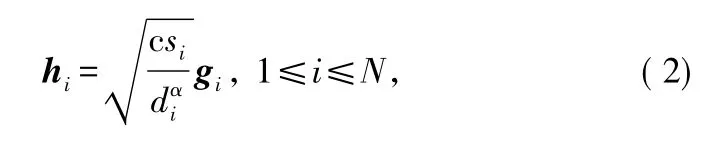
式中，c为常数;α为路径损耗指数;si为阴影效应，服从均值为零方差为σsh的正态分布，即10 log10si～;gi表示MS与DAUi之间的快衰落，且服从参数为mi的Nakagami分布，di是MS与DAUi之间的距离。

2 小区系统容量分析

2.1 基站功率受限时天线最优波束推导

针对DMIMO系统中DAUi功率受限问题，定义Φi为Mi×Mi对角矩阵，且只在Mi有连续的1，对角元素为0。为了方便描述，Mi在主对角线上的位置可表述为M1∶i－1+1到M1∶i，其中主对角线上元素M1∶k定义为:

DAUi功率受限下，传输信号协方差矩阵局部的迹可表示为:

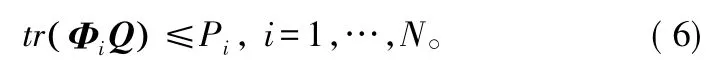
由于协方差矩阵Q对于天线最优波束的形成有很大关系。因此，在Pi功率受限情况下，可通过最大化系统传输速率的方法，获得最优输入协方差矩阵Q，具体数学建模如下:

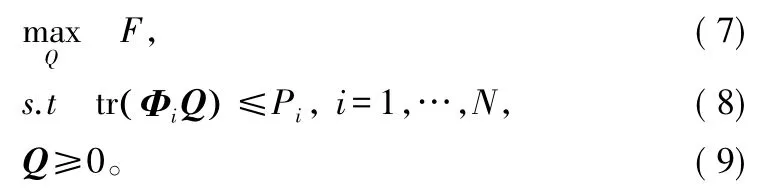
式(9)是半正定矩阵限制问题，为了解决此类问题，首先根据半正定矩阵性质即判断一个矩阵是否为半正定矩阵的充要条件是其所有主子式大于或等于零给出Q的二阶主子式矩阵Mij:

式中，qij表示Q的第i行第j列元素。主子式的获取是通过移除Q的M－2行(除了i行和j列)与相应的列。由于log(1+γ)是一个单调递增函数，最大化log(1+γ)相当于最大化γ。因此，上述数学建模可简化为:

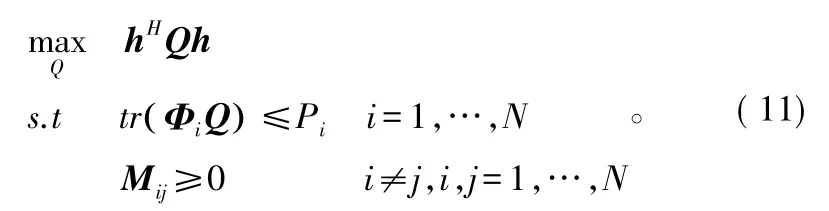
式(11)中Q的二阶主子式Mij≥0可等效为，采用拉格朗日乘子法可解决式(11)的优化问题，函数构造如下:

式中，μi和ηij表示拉格朗日乘子;假设κk= {M1∶i－1+1，…，M1∶k}定义为DAUk天线的索引。文献［8］推导过程可得出:

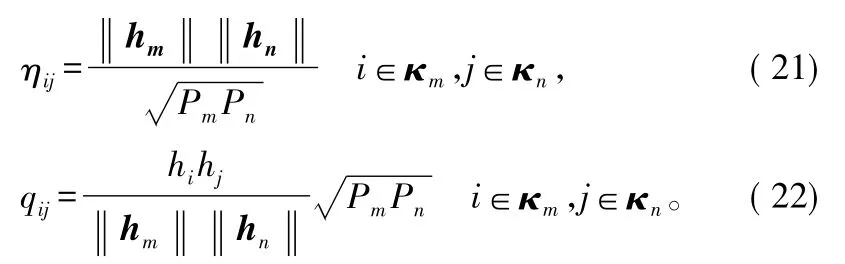
经过以上一系列的推导，可求出协方差矩阵Q*里的元素qii和qij，这是对式(11)的优化结果。为了描述本文MISO系统的最优波束向量的形成，下面采用奇异值分解法随其进行分析。假设Q*= WΛ WH，其中，W是单位矩阵，Λ是对角矩阵。由于Q*的秩为1，可求得Q*的非零特征值为P=∑Pi，相应的特征向量可表示为:

所以，发送信号向量x表达式为:

式中，sk表示发送符号，且满足均值为零方差为1。

2.2 小区平均遍历容量分析

对于单用户DMIMO系统，在发送端已知信道状态信息条件下，系统采用MRT方案对信号进行传输。在基站侧MRT相当于一种预编码，由上节基站功率受限知，DAUi形成的最优波束权重向量为:

式中，Pi表示DAUi的总功率。hi表示MS与DAUi之间的Mi×1复合衰落信道。接收端对接收信号进行MRC后，得到的信噪比(SNR)为:

式中，Mi为DAUi配置的天线数目，si表示阴影衰落，c表示一个常数，α表示路径损耗系数，di表示MS与DAUi之间的距离。gi表示MS与DAUi之间快衰落，且服从参数为m的Nakagami分布。

由于系统采用天线端口选择策略，即在N个DAU之间选择一个信道信息最好的DAUi进行信号传输，数学表达式可建模为:

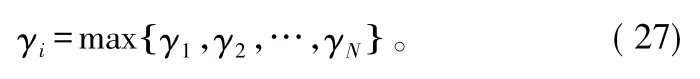
通过以上数学建模，可得到下行点对点遍历容量的表达式:

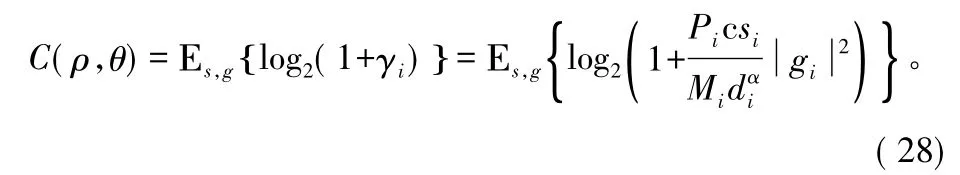
当x＞0时，f(x)=log2(1+x)是凸函数，应用Jensen不等式，可得到上式的下界:

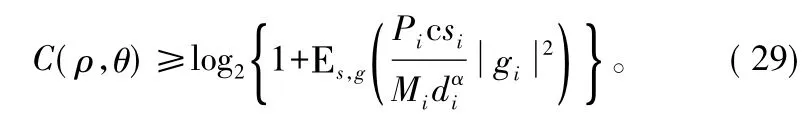
高信噪比下，上式可简化为:

经推导式(30)可表示为:

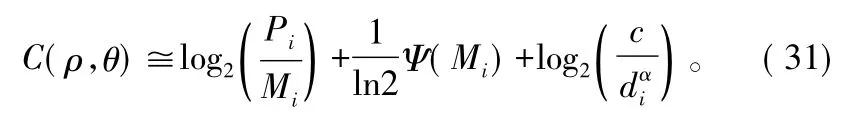
本节单用户小区遍历容量的推导，需要对用户位置进行统计平均。假设f(ρ，θ)是极坐标下MS在小区内分布的概率密度函数。则小区的平均遍历容量可以表示为:

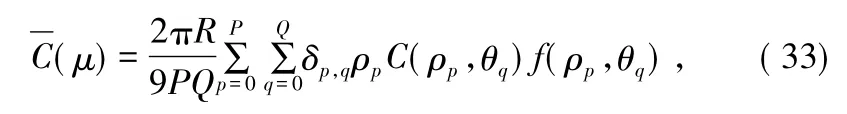
式中，P和Q是划分极半径和极角的等距节点数，δp，q是权值，为矩阵W的第p+1行，第q+1列的元素，矩阵W=[1 4 2 4…2 4 1]T⊗[1 4 2 4…2 4 1]。

3 计算机仿真与分析

由于本文小区天线位置优化问题是以小区平均遍历容量为优化目标，而用户在小区内的分布特征，对于求解小区平均遍历容量至关重要。因此，首先将建立一种类似于“热岛效应”的用户模型，来反映用户在圆形小区内的分布特征。“热岛效应”用户模型如图2所示。图2中将半径为R的圆形小区划分为城区与郊区2个区域，假设城区即Ψ1是中心坐标为(0，0)半径为r的圆，圆的其余部分为郊区记为Ψ2。假设MS在小区内分布的概率密度表达式为:

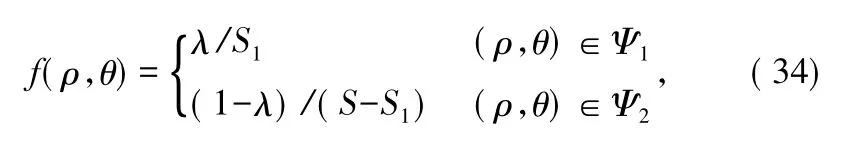
式中，S是整个圆形小区的面积，S1是城区的面积。λ∈［0，1］表示MS分布于城区的概率。从式(34)中不难发现，λ的取值不同所对应的MS在小区内的分布概率密度也不同，即λ的取值决定MS在小区内的分布情况。需要指出的是:当λ＞S1/S时，MS较集中分布在城区;当λ＜S1/S时，MS较集中分布在郊区;当λ=S1/S时，MS在圆形小区内服从均匀分布。

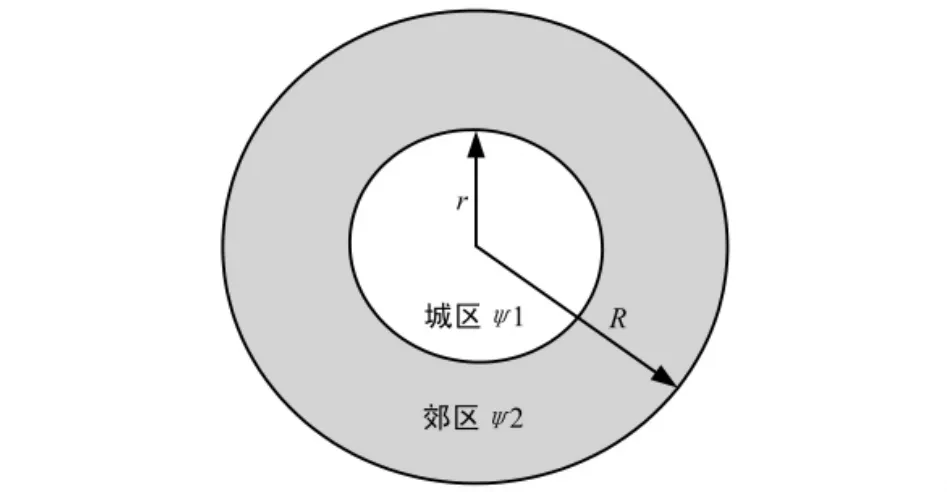
图2 “热岛效应”用户模型示意图

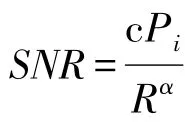
表1 主要仿真参数(单用户小区平均遍历容量)

MS均匀分布(λ=0．25)与非均匀分布(λ=0．6)下，对(1，3，1)DMIMO、(1，4，2)DMIMO和(1，5，4) DMIMO系统容量仿真性能曲线如图3和图4所示。从图中可看出，基站数目越多，且基站侧配置的天线数目越多，小区平均遍历容量越大。此外，MS无论是均匀分布还是非均匀分布，仿真值与理论值之间的误差都很小，从而可说明基于波束成形方案下所推导的单用户小区遍历容量的准确性。

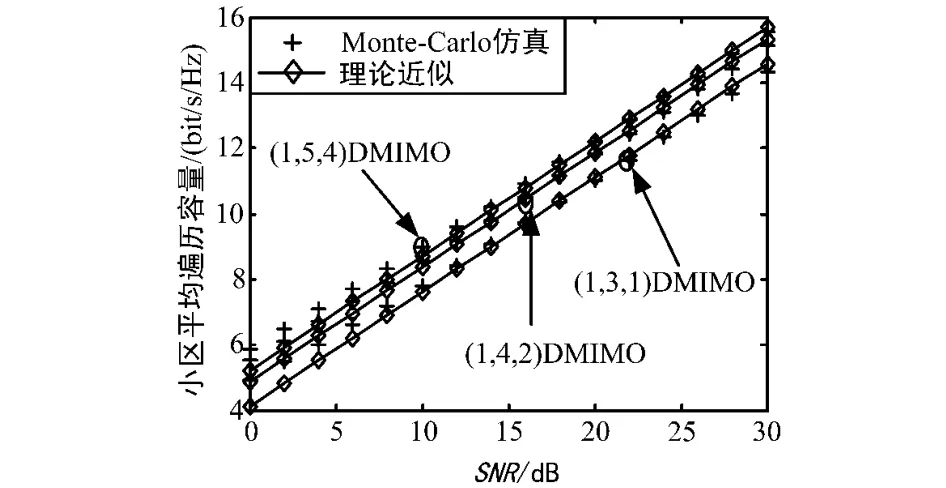
图3 λ=0．25单用户小区平均遍历容量

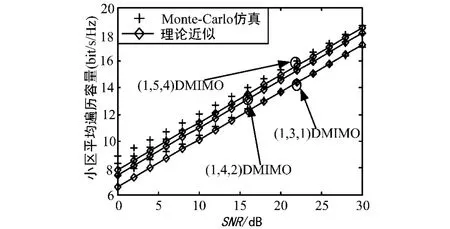
图4 λ=0．6单用户小区平均遍历容量

4 结束语

主要研究端口天线采用波束成形技术的DMIMO系统小区内多天线位置的优化问题。为此，首先分析了基站功率受限下，以最大化系统传输速率为目标，通过拉格朗日乘子法，推导天线权重向量即最优波束表达式。然后，基于智能天线波束成形方案，推导出单用户小区平均遍历容量理论表达式。仿真结果显示，所推导的理论公式与系统实际性能比较吻合。

［1］马庆鹏，徐家品．多小区多用户MIMO系统干扰对齐的优化[J]．无线电通信技术，2013，39(6):51－54．

［2］孙祥刚，颜彪，王加敏，等．基于MMSE算法的MIMO-OFDM系统频率同步[J]．无线电通信技术，2012，38(5):36－38．

［3］吕晓凯，胡铁森，万仁峰，等．MIMO-OFDM系统峰均比抑制技术的研究[J]．无线电通信技术，2013，39(1):49－51．

［4］Silverman Y，Smith F，Burns M．Coming together in Pain and Joy:a Multicultural and Arts-based Suicide Awareness Project[J]．The Arts in Psychotherapy，2013，40(2)．

［5］Gan J，Li Y，Zhou S，et al．On sum rate of multi-user distributed antenna system with circular antenna layout［C］∥Vehicular Technology Conference，2007．VTC-2007 Fall．2007 IEEE 66th．IEEE，2007:596－600．［6］Feng W，Xu X，Zhou S，et al．Sum rate characterization of distributed antenna systems with circular antenna layout［C］∥Vehicular Technology Conference，VTC Spring 2009．IEEE 69th．IEEE，2009:1－5．

［7］Choi W，Andrews J G．Downlink Performance and Capacity of Distributed Antenna Systems in A Multicell Environment[J]．Wireless Communications，IEEE Transactions on，2007，6(1):69－73．

［8］Lee S R，Moon S H，Lee I．Downlink Distributed Antenna Systems:Optimal Beamforming Designs and Capacity Behavior［C］∥Communications(ICC)，2012 IEEE International Conference on．IEEE，2012:2151－2155．

［9］Park E，Lee I．Antenna Placement for Downlink Distributed Antenna Systems with Selection Transmission［C］∥Vehicular Technology Conference(VTC Spring)，2011 IEEE 73rd．IEEE，2011:1－5．

［10］Wang X Z，Zhu P C，Chen M．Antenna Location Design for Generalized Distributed Antenna Systems[J]．IEEE Communications Letters，2009，13(5)，315－317．

［11］Vu M．MISO Capacity with Per-antenna Power Constraint[J]．Communications IEEE Transactions on，2011，59 (5)，1268－1274．

［12］Zhou S，Zhao M，Xu X，Wang J，et al．Distributed Wireless Communication System:A New Architecture for Future Public Wireless Access[J]．IEEE Commun．Mag，2003，41 (3):108－113．

Analysis on Average Ergodic Capacity of Distributed MIMO Downlink Cell System in Beamforming

FAN Chao1，CUI Lei2
(1．Unit 92117，PLA，Beijing 100072，China;2．Hohai University，Nanjing Jiangsu 211100，China)

This paper analyzes average ergodic capacity of distributed MIMO system downward district in beamforming．The composite fading channel model is established，including fast fading，shadow fading and path loss．Under the condition that the power of distributed base station is limited，the weight vector of each base station，namely the optimal beam，is derived．Based on ST-MRT transfer strategy，the expression of downward district point-to-point traversal capacity is derived under the condition of specific mobile station．Finally，considering the characteristics of arbitrary distribution of mobile station in the district，the approximate expression of average ergodic capacity of a district in beamforming is further derived．The simulation results show that the derived theory approximate expression can indicate the actual performance of the system．

Beamforming;DMIMO system;ergodic capacity

TN929．5

A

1003－3114(2015)05－21－4

10.3969/j.issn.1003－3114.2015.05.06

范超，崔磊．波束成形下DMIMO系统下行小区平均遍历容量分析［J］．无线电通信技术，2015，41(5):21－24，28．

2015－05－06

范超(1988—)，男，硕士研究生，主要研究方向:无线通信、图像处理。崔磊(1988—)，男，硕士研究生，主要研究方向:无线通信、信号处理。