压缩采样接收机抗ADC非线性影响的分析

王庆国，王华力，曾显华

(解放军理工大学 通信工程学院，江苏 南京 210007)

压缩采样接收机抗ADC非线性影响的分析

王庆国，王华力，曾显华

(解放军理工大学 通信工程学院，江苏 南京 210007)

针对宽带数字接收机易受模拟数字转换器(ADC)非线性的影响，研究压缩采样接收机在模拟数字转换器非线性影响下的性能。在深入剖析随机解调原理的基础上，通过对模拟数字转换器非线性的合理建模，分析了模拟数字转换器非线性因素对压缩采样接收机性能的影响。对比于传统数字接收机，压缩采样接收机得益于重构算法的优越性对模拟数字转换器非线性因素影响有更好的鲁棒性。仿真结果验证了上述理论分析。

宽带接收机；随机解调；ADC非线性；鲁棒性

0 引言

通常在通信、雷达、电子战等领域中，感知获取信号是基于奈奎斯特(Nyquist)采样定理，接收机的最低无失真采样频率至少为信号带宽的2倍。然而随着通信技术的发展，通信信号的带宽越来越大，这使得宽频带数字接收机需要更高速率的模拟数字转换器(Analog to Digital Converter，ADC)［1］，同时，实现宽频带信号的高精度采样对信息存储、传输、分析和处理带来压力［2］。2006年以来，学者们开始研究了压缩感知宽带数字接收机的实现模型，文献［3］和文献［4］最早提到了一种接收机实现的模型－随机解调(Random Demodulation，RD)，主要由混频器、积分器和ADC组成，实现宽频带稀疏信号的有效接收。文献［5］全面介绍了压缩采样接收机的工作原理，得出稳定重构原始信号的最小采样率远远小于奈奎斯特频率。

但在实际中压缩采样接收机受到许多非理想因素的影响，文献［6］概述了随机解调实现过程中各部分的非理想因素对系统的影响。文献［7］针对系统实现中积分器的非理想性进行了分析并找到弥补方法。文献［8］针对系统实现中存在的时钟抖动问题进入了深入的分析。但在宽带数字接收机实现中，ADC的非线性失真对系统性能的影响极大［6］。在压缩采样接收机的硬件实现中，ADC必定存在一定非线性特性，继而影响接收机的性能。压缩采样接收机在低速率采样下优势下，在抗ADC非线性影响方面是否优于传统的接收机是一个十分有意义的研究内容。

1 压缩采样接收机工作原理

压缩采样接收机框图如图1所示，其对原始信号进行采样过程分为3个步骤:①将原始信号f(t)与一个随机波形pc(t)相乘;②对相乘后的信号f(t)pc(t)进行积分运算;③对积分后的信号进行低速采样，得到最终的采样向量。

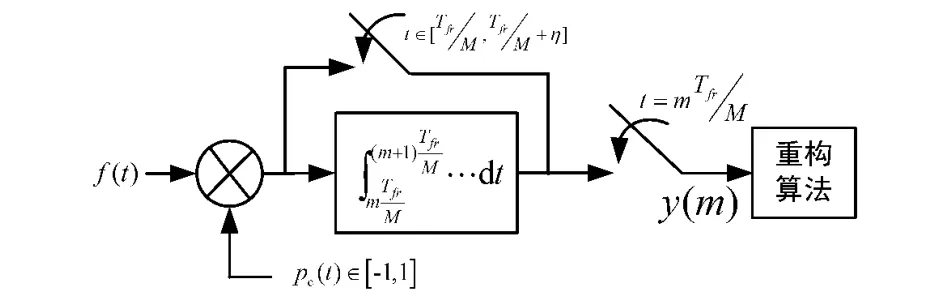
图1 随机解调框图

随机解调接收信号f(t)为带限稀疏多载波信号，其定义如下:

随机波形pc(t)是由随机数产生器产生的一个伯努利随机序列，该序列等概率得取值±1，且其变化频率不小于接收信号的奈奎斯特频率。积分器对解调输出信号进行积分，其功能等效于低通滤波器的作用。低速采样器的采样间隔T为随机解调采样区间的M分之一(M≪N)，且与积分时间相等。可知积分器冲激响应为:

则在相等的采样区间内，随机解调得到的采样向量长度为M，远小于奈奎斯特采样量N，实现了压缩采样y(m)，m=0，1，…，M－1。

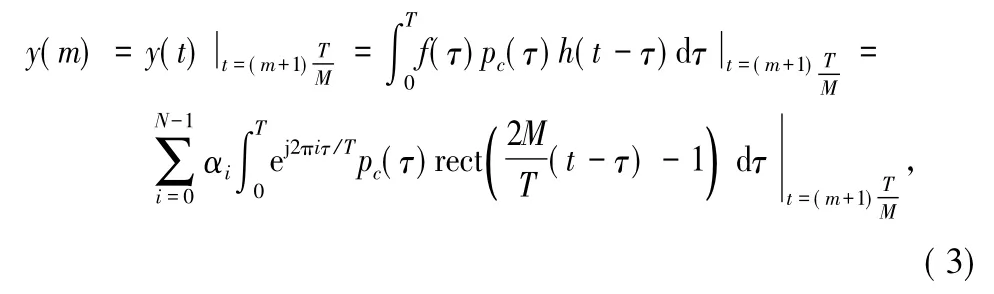
可知压缩采样接收机的压缩方程为:

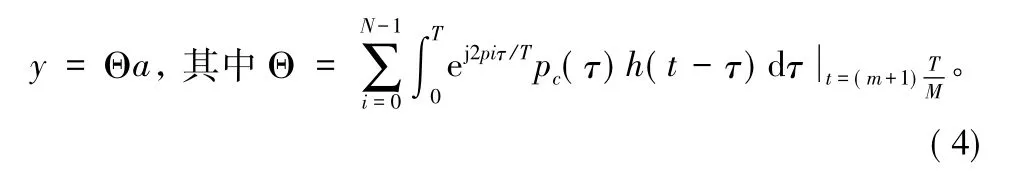
可见，采样向量纬度远远低于奈奎斯特采样向量纬度，实现了压缩采样。压缩感知理论的很多成熟重构算法能够直接应用到随机解调系统中，本文采用的是工程上广泛使用的正交匹配追踪算法［10］。

2 模拟信息转换器在接收机中的性能分析

2.1 模拟数字转换器的作用

在宽带数字接收机中模数转换器(ADC)是起着关键作用，其性能直接影响着接收机的性能。ADC的2个重要参数时钟频率fclcok和数据位的位数n分别衡量着宽带数字接收机的最大采样带宽和动态范围。

在宽带数字接收机中模拟到数字的转换主要由ADC完成，根据奈奎斯特采样定理，接收信号的带宽不得高于ADC采样时钟的一半，否则有信息损失。但受限于ADC本身制造的工艺，高速率的ADC难以实现高数据位，如表1所示，ADC本身的这种特性限制着接收机的性能。

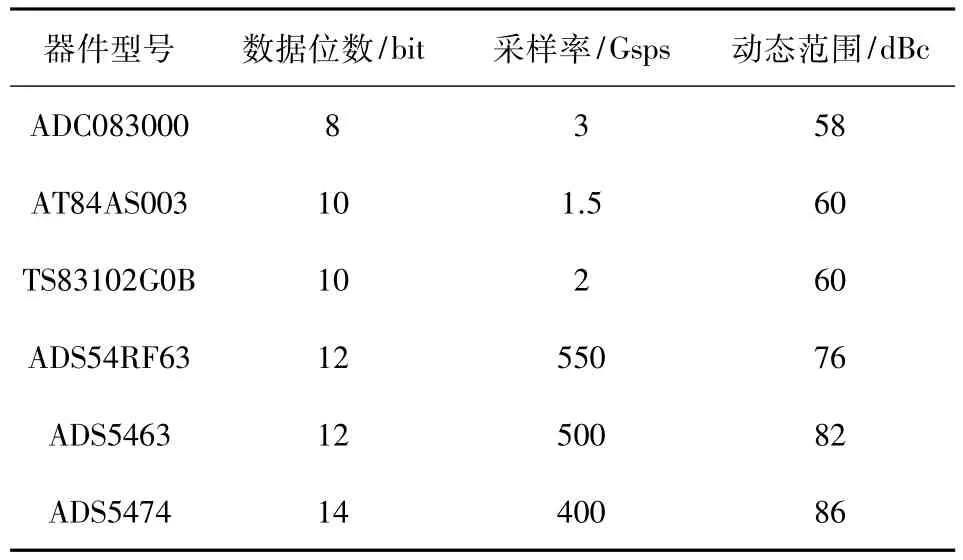
表1 现阶段高速ADC性能指标

现代宽带数字接收机多采用信道化并行处理的办法，将带宽化为多个子带宽，每一路只负责采样一个子带宽内的信号。这样以增加接收机复杂度为代价来换取采样带宽和，但信道化并行处理将大大增加接收机的功耗。因此需要寻找新的采样机制来代替传统的ADC采样，解决接收机采样带宽和动态范围的矛盾。

2.2 模拟数字转换器非线性的建模

压缩采样接收机可以实现宽带信号的低速处理，有效解决了宽带数字接收机对ADC的要求，但摆脱不掉ADC非线性的影响。在实际使用中，ADC表现出某种非线性特性，引进谐波和交调失真。式(4)是非线性特性曲线表达式，非线性失真引入了虚假的频率分量，尤其是三阶交调引入的失真，虚假频率分量接近信号频率分量，难以滤除，这将严重接收机中的性能。

本部分以无杂散动态范围(SFDR)为指标，重点考虑ADC非线性失真中的三阶交调失真，对比分析了ADC非线性对传统宽带数字接收机和压缩采样接收机的影响。

2种接收机系统受ADC三阶交调失真影响的建模框图如图2所示，三阶交调失真建模为:

式中，y为进入ADC的采样值，c3为三阶非线性失真系数，z为受干扰后的采样值．为了更好地比较2种接收机，输入到ADC的采样值都做归一化处理，y=y/max(abs(y))。

图2 接收机前端各阶段信号频谱示意图

传统数字接收机中，采样率为奈奎斯特频率fNYQ，则y=f(n/fNYQ)，对输入的采样值做归一化处理y=y/max(abs(y))，得到失真后的采样值:

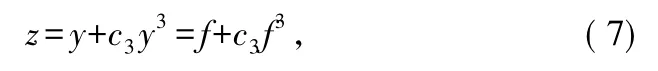
用采样值的DFT来估计传统接收机重构原始信号的性能好坏。

压缩采样接收机中，输入信号经过随机序列的解调、积分、低速采样得到压缩采样序列ycs=Θa= ΦΨa=Φf。对输入采样值做归一化处理ycs= ycs/max(abs(ycs))，则失真后的采样值z=ycs+ c3ycs3。用由失真后的采样值的重构信号来衡量压缩采样接收机重构原始信号的性能优劣。

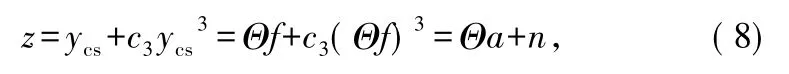
当压缩采样接收机各部分确定后，采样噪声是有界的，即‖n‖2≤ε。文献［11］证明对式(6)所示的含噪声的采样采样模型，正交匹配追踪算法同样可以精确重构信号，且证明重构误差的上限为:

式中，1≤k≤2，且与采样率大小有关，这样采样噪声对重构的影响能够得到控制。

3 数值仿真分析

仿真条件:假设接收信号为K稀疏的多载波信号，载波个数N=1 000。信号的频率界限为W= 2 GHz，则子载波间隔为Δf=W/N=2 MHz，帧长为T=1/Δf=2 500 ns，其位置是随机选择的且每隔Ts改变一次。

仿真1:仿真不同稀疏度的信号在不同采样率下的重构结果

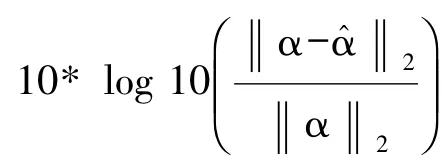
图3 不同稀疏度信号不同采样率的重构误差

仿真2:在信噪比为25 dB的条件下，对比两种数字接收机系统受ADC非线性的影响测试信号是由稀疏度K=2的随机信号，为保证重构成功，选取采样率为0．2。2种数字接收机下非线性失真对比如图4所示。三阶失真系数设置为c3=0．2。可以看出，传统接收机受到ADC非线性因素的影响产生了谐波和交调失真等虚假频率分量，SFDR=－16．48 dB。然而在压缩采样接收机中，受ADC非线性因素的影响产生虚假分量，但由于压缩采样理论的重构算法对采样噪声有很好的控制，使得重构误差大大减小，SFDR=－25．64 dB。

图4 25 dB下信号的频谱图

进行了5 000次仿真试验2种数字接收机的SFDR分布对比如图5所示。可以看出压缩采样接收机的SFDR得到了一定的改善，平均降低了10 dB。2种数字接收机在不同失真系数影响下SFDR对比如图6所示，可以看出在不同的非线性失真的影响下，压缩采样接收机相对于传统接收机，SFDR都有明显的提高，且与失真系数关系不大。

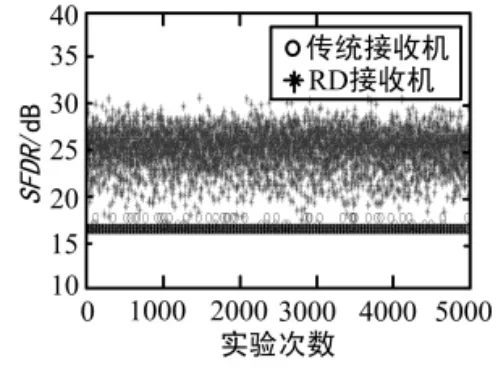
图5 2种接收机SFDR分布图

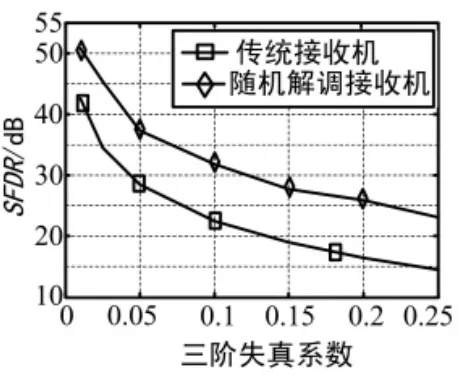
图6 2种接收机不同三阶失真系数下SFDR对比图

4 结束语

分析了ADC非线性因素对压缩采样接收机的影响，在压缩采样接收机中，ADC非线性因素的影响可以等效为采样噪声，由于压缩感知重构算法有较好的抗噪声能力，压缩采样接收机借助于重构算法对噪声的鲁棒性，使得其性能优于传统数字接收机，无杂散动态范围更大，这对宽带接收机有着重要的意义。

［1］于楠．压缩感知宽带数字接收机关键技术研究[D]．哈尔滨:哈尔滨工业大学，2013:18－25．

［2］石光明，刘丹华，高大化，等．压缩感知理论及其研究进展[J]．电子学报，2009，37(5):1070－1081．

［3］Kirolos H，Laska J N，Wakin M，et al．Analog-to-information Conversion via Random Demodulation［C］∥Design，Application，Integration and Software:IEEE Press，2006:71－74．

［4］Laska J N，Kirolos S，Duarte M F，et al．Theory and Implementation of an Analog-to-information Converter using Random Demodulation［C］∥Circuits and Systerms: IEEE Press，2007:1959－1962．

［5］Tropp J A，Laska J N，Duarte M F，et al．Beyond Nyquist: Efficient Sampling of Sparse Bandlimited Signals[J]．IEEE Trans．Inf．Theory，2010，56(1):520－544．

［6］Kirolos S，Ragheb T，Laska J N，et al．Practical Issues in Implementing Analog-to-information Converter［C］∥the 6th International Workshop on System on Chip for RTA．IEEE Press，2006:141－146．

［7］Chen Y，Mishali M，Eldar Y C，et al．Modulated Wideband Converter with Non-ideal Lowpass Filters［C］∥Speech，Signal Process．(ICASSP)．IEEE Press，2010:3630－3633．

［8］Abari O，Lim F，Chen F．Why Analog-to-information Converters Suffer in High-bandwidth Sparse Signal Application[J]．IEEE Trans on Circuits and Systerms．2013，60 (3):2273－2284．

［9］Lee T H．The Design of CMOS Radio-frequency Integrated Circuits，2nd Edition[J]．Communications Engineer，2004，2(4)．

［10］Tropp J A，Gilbert A C．Signal Recovery from Random Measurements via Orthogonal Matching Pursuit[J]．IEEE Transactions on Information Theory，2007，53(12):4655－4666．

［11］Emmanuel J．Candès Justin K．Romberg Terence Tao．Stable Signal Recovery from Incomplete and Inaccurate Measurements[J]．Comm．Pure Appl．Math．，2006，59(8): 1207－1223．

Analysis of Random Demodulator Receiver Against ADC Nonlinearity

WANG Qing-guo，WANG Hua-li，ZENG Xian-hua
(College of Communication Engineering，PLA University of science and technology，Nanjing Jiangsu 210007，China)

For the wideband digital receiver is susceptible to Analog to Digital Converter(ADC)nonlinear influence，Research random demodulation receiver performance under the influence of the ADC nonlinear．This paper was based on deep understanding the working principle of Random Demodulation，modeled reasonably to ADC nonlinearity，analyzed how ADC nonlinearity impact the random demodulation．Comparing to traditional digital receiver，Random demodulation had a better robustness to ADC nonlinearity because of the reconstruction algorithm．Simulation results verified the above theoretical analysis．

wideband receiver;random demodulator;ADC nonlinearity;Robustness

TN911．72

A

1003－3114(2015)05－25－4

10.3969/j.issn.1003－3114.2015.05.07

王庆国，王华力，曾显华．压缩采样接收机抗ADC非线性影响的分析［J］．无线电通信技术，2015，41(5):25－28．

2015－05－18

国家自然科学基金项目(61271345)

王庆国(1989—)，男，硕士研究生，主要研究方向:信息感知、处理与对抗。王华力(1967—)，男，教授，博士生导师，主要研究方向:信息感知、处理与对抗。