水泥搅拌桩加固山间软土沉降简化计算方法探讨

冯 环，刘平平，邓通发

(1．滁州职业技术学院土木工程系，安徽滁州 239000；2．江西理工大学建筑与测绘工程学院，江西赣州 341000)

水泥搅拌桩加固山间软土沉降简化计算方法探讨

冯 环1，刘平平2，邓通发2

(1．滁州职业技术学院土木工程系，安徽滁州 239000；2．江西理工大学建筑与测绘工程学院，江西赣州 341000)

采用不同的典型简化计算方法对井冈山厦坪至睦村（赣湘界）高速（简称井睦高速）公路中四个典型断面处的水泥搅拌桩复合地基进行了计算，并与现场实测结果进行对比分析．结果表明，加固区采用复合模量法联合下卧层用应力扩散法更为接近实测值，复合地基的沉降计算是合理的．

复合地基；沉降；软土

水泥深层搅拌桩处理软土地基的方法因其造价低、施工简单、应用范围广等优点，近几年被广泛应用于地基加固工程中，特别是应用于淤泥质土、淤泥、粘性土、粉土、杂填土等软弱地质的加固工程．与此同时，一些问题也日益凸显出来，如因施工单位对工艺控制不严格，使得搅拌不均匀，水泥实际掺入比和水泥强度等级降低，搅拌桩强度不能达到设计要求等等，从而导致复合地基的桩体强度不够，最终反映到现场就是沉降过大的问题，因此复合地基的沉降控制是工程界人员的研究重点．复合地基的沉降计算方法经过几十年的发展，虽已有了一套比较完整的理论体系，但还是远远落后于工程实践[1]，特别是针对不同的地质条件，各种方法的适用性还没有统一的规定，对于土-砂混合地区的深层水泥搅拌桩复合地基的沉降研究更较少见．笔者将采用不同的典型简化计算方法对井睦进行实例计算，并将计算结果和长期的观测沉降结果进行对比分析，总结各种简化计算方法的特点，以期为相同地质条件下软土地基处理技术的设计和施工提供一些借鉴．

1 简化计算方法简介

文献[2]对水泥搅拌桩复合地基的沉降计算做了详细的介绍，通常认为其褥垫层刚度大，产生的压缩量很小，将其忽略不计．因而在各个实例简化计算过程中，往往将复合地基视为由加固区的变形量S1和下卧层的变形量S2组成的双层地基[3-9]，其沉降量可表示为S=S1+S2．简化计算时常采用复合模量法、应力修正法、桩身压缩量法等方法来计算加固区的沉降量S1，用分层总和法计算下卧层的变形量S2．在使用分层总和法计算下卧层沉降时，因其下卧层顶面的附加应力难以精确计算，计算时常采用应力扩散法、等效实体法、当层法等方法简化．具体见表1．

表1 常用复合地基沉降计算方法

1.1 加固区计算方法

复合模量法：此法将复合地基加固区桩体和土体看成一个复合土体，采用复合压缩模量Eci来评价复合土体的压缩性，并采用分层总和法计算加固区土层压缩量S1：

式中，n为加固区分的层数，Δpi为第i层复合土上附加应力增量，Hi为第i层复合土层的厚度．复合土变形模量Ec采用面积加权平均法计算，即：

式中，Ep为桩体变形模量，Es为桩间土变形模量，m为置换率．

应力修正法：复合地基因有增强体的存在使得作用在桩间土上的荷载密度比作用在复合地基上的平均荷载密度要小．应力修正法考虑桩体和桩间土构成复合地基，认为可以忽略桩体的存在，按照桩间土的变形模量Es，乘以应力修正系数，得到加固区的变形模量，采用分层总和法计算加固区土层的压缩量，其计算公式为：

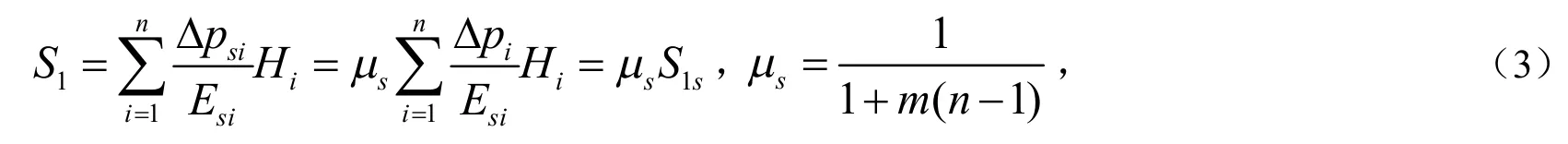
式中，sμ为应力修正系数，Δpsi为复合地基中第i层桩间土的附加应力增量，Δpi为天然未加固地基在荷载P作用下第i层土上的附加应力量，S1s为天然未加固地基在荷载P作用下荷载相应厚度内的压缩量．

桩身压缩量法：在荷载作用下复合地基加固区的压缩量也可通过计算桩身压缩量来得到．设桩底端刺入下卧层的沉降变形量为Δ，则相应加固土层的压缩量的计算式为：

式中，pμ为应力集中系数，SP为桩身压缩量．

复合模量法因未考虑桩体和桩间土在荷载作用下共同作用引起的复合模量的改变，复合模量实际上要比计算中按桩体模量和桩间土的面积加权之和大，采用复合模量法计算基础沉降时，复合地基的性状越接近均质体，桩土之间受力变形越协调，二者越能够共同抵抗变形，采用这种方法越符合实际．应力修正法虽然形式简单，但在设计计算中应力修正系数sμ是较难合理确定的．复合地基置换率m值是设计人员确定的，应该说是明确的，但桩土应力比n值的影响因素较多，很难选用合理值，特别是当桩土相对刚度较大时．桩身压缩量法需要计算桩身的应力，但是桩身应力计算牵涉到摩阻力的分布、端承力的大小以及桩顶应力等极难获得的量值，即使在最为简单的情况下，如假设摩阻力均匀分布和端承力为零的情况，也要牵涉到计算桩土应力比n值，且n值不易获得．

1.2 下卧层计算方法

下卧层土层压缩量的计算常采用分层总和法计算，即

在计算过程中，要确定上式中复合地基下卧层的附加应力增量Δpi，而作用在下卧层土体上的荷载是很难精确计算的，在工程应用上时常采用应力扩散法、等效实体法、当层法等进行计算其荷载．

压力扩散法：如图1所示，若复合地基上作用荷载为p，复合地基加固区压力扩散角为β，则作用在下卧土层上的荷载p可用下式计算：

式中，B为复合地基上荷载作用宽度，D为复合地基上荷载作用长度，h为复合地基加固区厚度．计算时应力扩散角取值可参考规范[10]中表5.2.7确定．

等效实体法：将复合地基加固区看成一个等效实体，作用在下卧层上的荷载与作用在复合地基上的相同．如图2所示．

式中，pt为复合地基加固区下卧土层上荷载密度，f为等效实体四周侧摩阻力密度．

应用等效实体法计算复合地基下卧层顶面荷载的关键是周围土体对等效实体摩阻力的确定，目前还没有一个被普遍接受的确定方法．

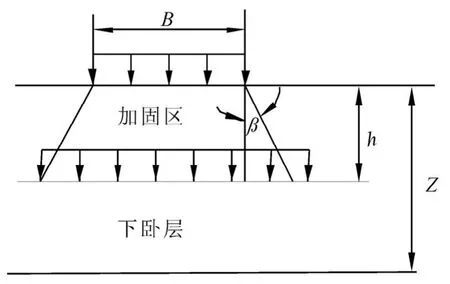
图1 应力扩散法示意图

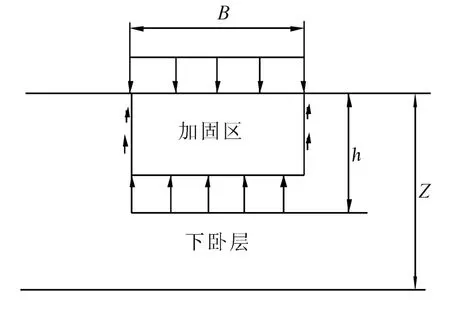
图2 等效实体法示意图

当层法：采用当层法计算复合地基在荷载作用下地基中的附加应力时，加固层复合模量为Ecs，下卧层土体模量为Es，可将加固层换算成与下卧层模量相同的土层，然后按天然地基计算附加竖向应力，其当层厚度h1为：

2 井睦工程实例

井睦高速公路工程位于井冈山市厦坪至睦村段，区段线路全长43.3公里，山涧沟谷发育并形成1.0 – 10.0米厚淤泥质土-砂混合软土，下伏基岩为全、中风化花岗岩．本文选取典型地质条件下4个桩号路段进行基底沉降观测及理论计算，此4个桩号路段均为沟谷洼地，发育成的土砂混合软土较厚（具体地质参数见表2），而且路堤填土高度高达10余米，为使路堤达到稳定，施工单位采用现场搅拌水泥土桩的加固处理措施．水泥搅拌桩布置形式为梅花形，且打入持力层至少为0.5米，现场搅拌桩径为0.5米，桩间距为0.5米，水泥参入比为10% – 13%．现场荷载实测显示，桩地基14天承载力平均约为663 kPa，大于设计承载力550 kPa，90天承载力大于1 100 kPa，桩体满足设计要求．桩土应力比平均为n=11．水泥搅拌桩桩体压缩模量采用规范[11]取Ep= (100～120) fcu= 180 MPa．

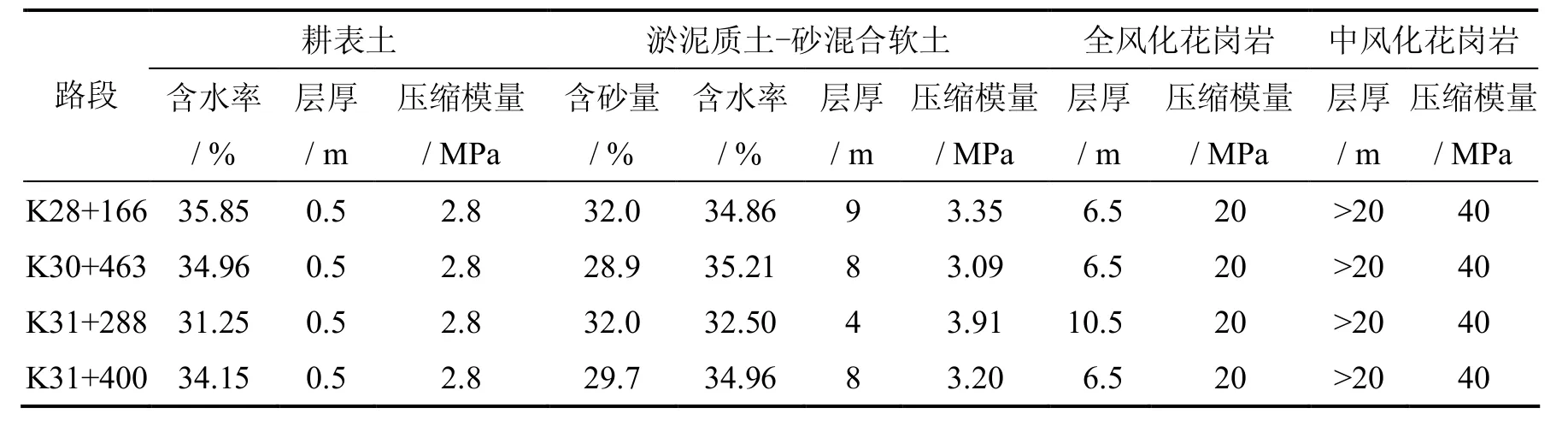
表2 典型地质条件计算参数

沉降计算时计算深度的取值有两种选择，可采用应力比法或变形比法．应力比法一般按附加应力zσ小于0.1 – 0.2倍的自重应力σcz来控制压缩层深度，但没考虑土层的构造和不同压缩性的影响，如在地层深部的硬层中，由于压缩性低，土层的变形急剧减小，同时由于硬层的扩散应力作用，硬层以下土层的变形也就很小了，但如按应力比的方法，则压缩层的深度远大于硬层的深度．在软土地区高速公路沉降计算中按应力比法确定的压缩层深度过大．现行规范[12]采用变形比法来确定压缩层厚度比较符合实际，即：

式中，k为地基分层总数，Δsk为从压缩层底向上取1.0 m的土层计算的最终变形量（mm），Δsi为第i层土层的最终压缩变形量（mm）．

笔者将各类参数代入简化计算方法计算，得出水泥搅拌桩复合地基的最终沉降结果，见表3．

3 计算与实测沉降对比

3.1 实测沉降

观测人员采用电子水准仪在路堤填筑、预压及路面施工过程中进行沉降监测．首先确定观测断面，观测小组沿线路选择了四个典型的断面进行观测，四断面分别在桩号K28+166、K30+463、K31+288及K31+400处．断面确定后，观测小组结合观测目的，在每个断面找一个基准点并假定其高程，基准点用水泥混泥土制作布设在路基一百米外的一个稳定位置，保证不会因人为等因素改变其高程；根据监测要求，在路基各观测横断面的路基中心线、左线中、右路肩处埋设了桩土沉降板，如图3，每组2个，分别布置在桩中心和桩间土形心处．沉降板由钢底板、金属测杆和保护套管组成，安装时其竖管的垂直度偏位不大于2%，其内部观测管和保护管可根据工程填土施工的进展逐节加高．在初次测量确定其原始标高以后，每填筑一米观测一次．观测人员对四个断面从路堤填筑、预压到路面施工全过程进行了长期的沉降观测，其荷载-时间-沉降图见图4和图5，累积沉降-时间图如图6所示．

表3 四典型桩号路段处水泥搅拌桩复合地基沉降计算结果

从图4和图5可知，水泥搅拌桩复合地基的沉降主要发生在路基填筑施工期间，在路面施工完两个月之后沉降基本趋于稳定状态．从图6知，在填筑完后，路基底部复合地基的沉降将趋于稳定状态，其各断面处的累积沉降：桩号K28+166处为169 mm，桩号K30+463处为162 mm，桩号K31+288处为128 mm，桩号K31+400处为131 mm．

3.2 对比分析

3.2.1 加固区的沉降计算分析

由于工程中下卧层为风化花岗岩土层，具有较高的压缩模量，即桩端落在较硬的土层上，向下的刺入变形很小，加固区土砂混合性状接近均质体，搅拌桩和土体之间易于变形协调，能够充分发挥桩体的作用，桩土能够共同抵抗变形．因此，采用复合模量法计算加固区的沉降变形量值是较合理且偏安全的，现有规范也推荐此方法．大量工程实践[13]也表明，当面积置换率高于20%，且桩端土质较好，桩体刺入变形很小时，该方法计算值与实测值较相近．而应力修正法的沉降计算值远大于其它方法的计算结果，较实测值也明显偏大，这是因为其忽略了加固区桩体增强作用的存在，且桩土应力比的影响因素较复杂，难以得到较合理的n值．大量的测试结果表明[14]，无论是刚性基础还是柔性基础，桩土应力比并非常数，它的大小及变化规律随荷载、地基土性质以及基础刚度的变化而变化，桩土应力比值在3 – 16之间变化，所以确定合理的n值对于这种计算方法是非常重要的．桩身压缩量法也存在与应力修正法类似的问题，且桩体刺入下卧层的刺入量很难确定，本文考虑到下卧层压缩模量较大，从而忽略刺入变形，其计算结果偏小，用于工程实践中会过于保守，实用性较差．

图3 工程现场沉降监测示意图

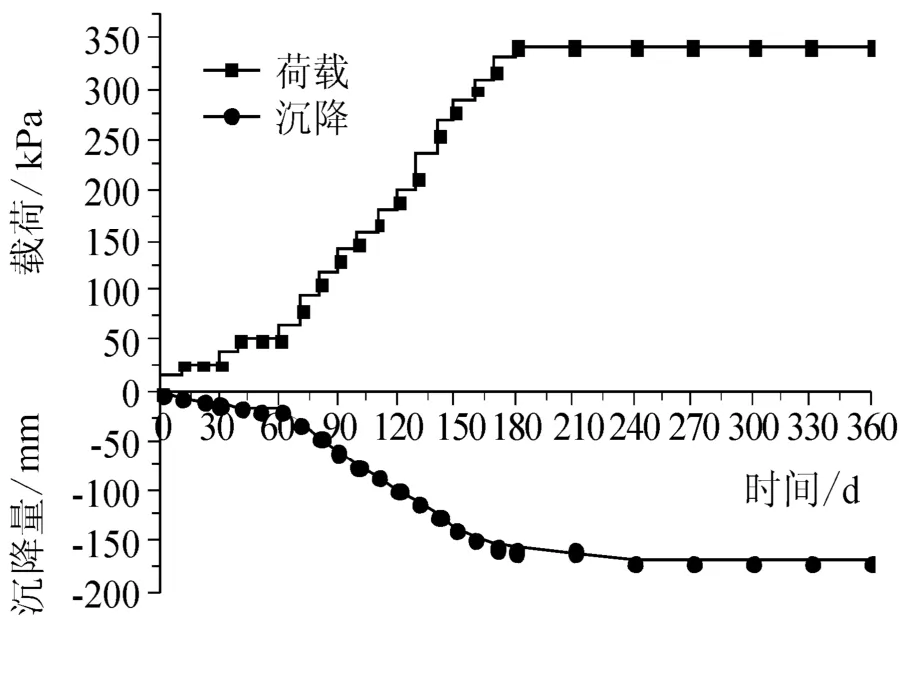
图4 K28+166处涵洞荷载-时间-沉降图

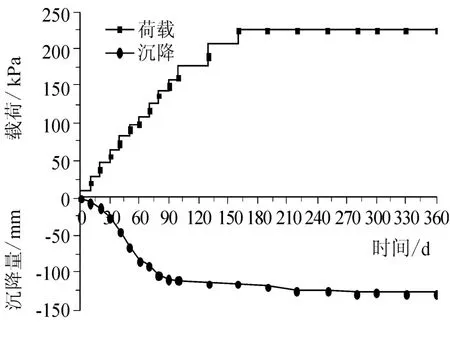
图5 K31+288处涵洞荷载-时间-沉降图

图 6 四典型地段累积沉降-时间图

3.2.2 下卧层的沉降计算分析

对于下卧层的沉降计算，由于沿线是路堤荷载，z/ b＞10，可简化为平面应变来计算下卧层的附加应力，其最大难点在于下卧层上附加应力的确定．应力扩散法中的应力扩散角是其主要考虑的问题[15-16]，本文应力扩散角取值为β=30°，最后沉降计算结果较小，但与加固区的复合模量法结合后，其计算结果与实测值很接近．由于水泥搅拌桩与软土相对刚度的不确定性，侧摩阻力分布非常复杂，受桩土相对刚度的影响很大，很难确定一个合理的取值，从而引起等效实体法较大的计算误差，本文的计算结果要偏大．在竖向荷载作用下，当层法是基于双层地基中的附加应力来进行沉降计算的，相比复合地基而言，应力扩散作用双层地基的效果较好，但计算结果仍存在一定的误差，但从本文计算结果看，结果偏大但误差小于等效实体法的．

3.3 压缩模量的修正

从水泥深层搅拌桩复合地基的沉降计算中可看出，加固区或者下卧层的土体压缩模量取值对计算结果影响很大，压缩模量的取值需要注意以下问题：

1）土的压缩模量是个变量，会随着应力历史及压力范围的变化而变化．现有的沉降计算方法中，土体压缩模量一般取值为E1-2，即以压缩曲线上100 – 200 kPa压力范围割线斜率作为压缩模量值[17-18]．但随着对复合地基中土体压缩特性的深入研究，对于路堤荷载下深层搅拌桩复合地基的土层中，土体受附加应力远远高于100 – 200 kPa的压力范围值[19]，若仍采用E1-2作为土体压缩模量进行沉降计算，必然存在较大的误差．因此，可采用压缩曲线上200 – 300 kPa压力范围割线斜率作为压缩模量值，即E2-3．

2）不能忽视水泥浆的渗透和扩散作用对土体特性的影响．沈锦儒①沈锦儒. 水泥土搅拌桩复合地基综合试验[C] // 第六届全国地基处理学术讨论会暨第二届全国基坑工程学术讨论会论文集. 西安: 西安出版社, 2000.通过研究发现，水泥搅拌桩施工后，复合地基桩间土的物理力学特性会发生变化，其中含水量和孔隙比减小，从而改善了压缩性能，使压缩模量提高．此外，水泥搅拌桩对桩间土也有一定的挤土作用，这有利于提高其压缩模量．

4 结 语

针对本工程实例而言，花岗岩山间软土水泥搅拌桩复合地基的沉降计算采用联合复合模量法与应力扩散法的沉降计算结果较接近于实测值，误差较小且安全，且易从工程中获得相关计算参数，简单实用性较好；其它方法的计算因计算参数取值等问题，计算结果较实测值差距较大，实用性不好．

工程中水泥搅拌桩作用使桩间土的土质特性得到改善，提高了压缩模量，在沉降计算时如果仍采用原软基土体压缩模量，结果会与工程实际不符，必然存在较大的误差．因此，需要合理修正土体压缩模量．作者建议加固区土层压缩模量采用施工后的桩间土压缩模量E2-3值．

[1] 何思明, 温志云. 半刚性桩复合地基的工作特性[C] // 龚晓南. 复合地基理论与实践学术讨论会文集. 杭州:浙江大学出版社, 1996: 47-51.

[2] 龚晓南. 复合地基设计和施工指南[M]. 北京: 人民交通出版社, 2003: 28-34.

[3] 刘添俊. 路堤式道路水泥搅拌桩复合地基沉降分析[D]. 广州: 广东工业大学土木与交通工程学院, 2005: 15-17.

[4] 李海芳. 路堤荷载下复合地基沉降计算方法研究[D]. 杭州: 浙江大学岩土工程研究所, 2004: 12-16.

[5] 倪红. 搅拌桩复合地基沉降计算方法分析[J]. 工业建筑, 2008, (s1): 755-757.

[6] 张渭波, 鼠磊. 复合地基沉降计算传统方法参数取值研究[J]. 河南科学, 2010, 28(9): 1161-1163.

[7] 张钢. 水泥搅拌桩复合地基沉降计算[J]. 土工基础, 2010, (4): 67-70.

[8] 李舒瑶, 王俊. 复合地基最终沉降量计算方法研究[J]. 河南大学学报: 自然科学版, 2007, 37(1): 95-98.

[9] 陈莉娟. 水泥土搅拌桩复合地基沉降组成及其计算方法研究[J]. 黑龙江科技信息, 2011, (23): 238-238.

[10] GB 50007-2002 建筑地基基础设计规范[S].

[11] JGJ 79-2002 建筑地基处理技术规范[S].

[12] JTJ 017-96 公路软土地基路堤设计与施工技术规范[S].

[13] 王国光, 严平, 龚晓南. 考虑共同作用的复合地基沉降计算[J]. 建筑结构, 2002, 32(11): 67-69.

[14] 陈甦, 陈国兴. 水泥土桩复合地基研究综述[J]. 中外公路, 2007, (3): 34-41.

[15] 易耀林, 刘松玉. 路堤荷载下复合地基沉降计算方法探讨[J]. 工程力学, 2009, 10: 147-153.

[16] 曾德淼. 路堤荷载下成层地基中粘结材料桩复合地基沉降计算研究[D]. 长沙: 湖南大学岩土工程研究所, 2012: 19-27.

[17] 钱玉林. 水泥加固土复合模量的研究[J]. 工业建筑, 2001, (2): 31-33.

[18] 张敏静. 路堤荷载下复合地基桩土相互作用特性及沉降计算方法研究[D]. 成都: 西南交通大学土木工程学院, 2011: 9-13.

[19] 赵明华, 胡增, 张玲, 等. 考虑土拱效应的高路堤桩土复合地基受力分析[J]. 中南大学学报:自然科学版, 2013, (5): 2047-2052.

The Probe into Simplified Calculating Method of Intermontane Mollisol Sedimentation with Cement Mixing Pile

FENG Huan1, LIU Pingping2, DENG Tongfa2
(1. Department of Civil Engineering, Chuzhou Vocational and Technology College, Chuzhou, China 239000; 2. School of Architectural and Surveying and Mapping Engineering, Jiangxi University of Science and Technology, Ganzhou, China 341000 )

This paper takes a comparative analysis of the results between the different typical simplified calculating methods and the field tests in Xia Ping Village of Jinggangshan to Mu Cun Village between Jiangxi province and Hunan province. There are four typical cement mixing pile composite foundations on the highway (short for Jing-Mu highway). The results indicate that it is reasonable for the sedimentation calculation of composite foundations. Such a calculation is much closer to the measured value by means of the composite modulus method combined with the underlying stretums diffusion method.

Composite Foundation; Sedimentation; Mollisol

TU470+.3

A

1674-3563(2015)01-0045-08

10.3875/j.issn.1674-3563.2015.01.008 本文的PDF文件可以从xuebao.wzu.edu.cn获得

(编辑：王一芳)

2014-06-28

江西省交通厅科技项目(2012C0004)

冯环(1979- )，女，河北辛集人，讲师，硕士，研究方向：岩土工程和地基处理