基于复杂网络病毒传播模型的免疫策略研究

关风娇，陈新一

(西北民族大学中国民族信息技术研究院，甘肃兰州730030)

基于复杂网络病毒传播模型的免疫策略研究

关风娇，陈新一

(西北民族大学中国民族信息技术研究院，甘肃兰州730030)

复杂网络理论促进了病毒传播的进一步认识，文章基于复杂网络中免疫策略理论提出了改进的免疫方法——三阶双免疫策略.它是对网络中任意抽得的节点中最大度节点及其三阶邻居节点一起实施免疫策略，是对双免疫策略的进一步改进.研究发现，与传统的随机免疫、经典的熟人免疫策略、二阶双免疫策略相比，文章提出的三阶免疫获得了较好的免疫效果.

复杂网络；免疫策略；三阶双免疫；无标度网络

0 引言

病毒的传播处处可见，在生物界和计算机等众多领域得到了广泛关注，在复杂网络中个体被抽象为节点，它们的链接被视为边，这些理论知识增加了学者对病毒传播的认识，推动了免疫策略研究的进程.复杂网络是一个包含大量个体及其个体间相互作用的复杂系统[1]，把复杂网络理论应用于病毒传播模型的研究，进而继续用该知识建立免疫策略，为控制病毒传播做贡献就显得非常有价值.

下文在叙述复杂网络病毒模型的种类和复杂网络中比较经典的传统免疫策略后，提出改进的三阶双免疫思想，并重点论述依据该算法思想进行的仿真实验及其与经典的熟人免疫[2]、双免疫[3]、二阶双免疫策略[4]进行免疫效果的对比分析.

1 复杂网络上的病毒传播模型

经典的病毒传播模型中个体状态通常有：S(susceptible)——易染状态(通常称为健康状态)[5]；I(infected)——感染状态；R(removed)——免疫状态(也称作被移除状态)[2].依据种群个体感染病毒后的情况，经典病毒传播模型有SI模型、SIS模型、SIR模型、SIRS模型、SEIR模型[6,7].

1.1 SI模型

定义t时刻网络节点中易被感染节点数为S(t)，感染节点数为I(t)，网络节点总数用N表示，定义单位时间节点从易染状态染上病毒处在感染状态的几率为α，则描述SI模型的微分方程为[6,7,8]：

1.2 SIS模型

1.3 SIR模型

1.4 SIRS模型[6,7]

1.5 SEIR模型[6,7]

2 复杂网络经典免疫策略

无标度网络特性——度数小的节点约占整个网络节点数的78%,大于等于4度的节点约占22%[10].现实中许多网络都遵循此特性，从此特性不难得出与小度节点相比大度节点感染后，更能造成大范围的传播，基于此特性的网络的经典免疫策略主要有：随机免疫、目标免疫、熟人免疫等[2].

2.1 随机免疫

随机免疫是最简单的免疫策略，该技术是任意抽得一些节点进行免疫，又称为均匀免疫，意思为所有节点被选取进行免疫的几率相同，由此也可想而知,此免疫效率不高，若想彻底使全部节点处在移除免疫状态，则必须把此策略实施到全部节点.

2.2 目标免疫

目标免疫[11]采取抓大策略，即对网络中的节点度数排序，选取最大度节点实施免疫策略.但现实中的网络结构复杂，网络节点数目巨多，网络连接关系实时动态变化，因此可以说这种策略属于理想化方法，实现的可能性较小.

2.3 熟人免疫

熟人免疫策略[12]其免疫效果优于随机免疫，该方法主要指先按照一定百分比任意选取节点，然后对这些节点的任意邻居实施免疫策略.此种免疫策略不必获取该网络所有节点度的全局概况，弥补了目标免疫的缺点.

此外，还有双免疫策略[3]：按照一定百分比随机选取节点，对被选节点本身及其最大度[8]邻居进行免疫的技术.

二阶双免疫策略是对任意抽得节点的度最大的节点和二阶邻居节点实施免疫的策略[4]，由于选取的最大度节点数目增多，涉及相连的邻居节点数目增多，所以免疫效果要优于双免疫策略.

3 三阶免疫算法的提出

三阶免疫算法思想是在研究无标度网络特性和二阶双免疫策略思想基础上提出的.该算法的思想为：从节点总数为N的无标度网络模型中，按照百分比d任意抽得一些实验节点并求出度，得到最大节点的一阶邻居最大度节点、二阶邻居最大度节点和三阶邻居最大度节点，同时对这些实验中的最大度节点和三阶邻居最大度节点进行免疫.

选择这样的矩阵表示节点是否有链接的数组，该矩阵主对角线数字代表节点度数，其他位置数字含义为：若两节点ai、aj有链接关系,则aij=aji=1，否则aij=aji=0[4].三阶免疫策略实施过程为：

1) 构建无标度网络模型，设定网络节点总数N为1 000.

2) 按照任意设定的百分比d，以任意抽得的n=Nd个节点作为数组元素.

3) 进行三阶免疫技术方法的仿真实验：①根据对角线数字找出n个节点中度最大的节点，及其一阶、二阶、三阶最大邻居节点，把该最大度节点及其一阶、二阶、三阶最大邻居节点所在矩阵中的行和列非零元素全部设置为零，设置后得到新的数组.②重复上述过程直到数组中所有元素都实施了三阶免疫策略.

4) 构建新的网络拓扑结构.

4 仿真实验与对比分析

仿真实验流程图为：

图1 仿真实验流程图

图2 起始节点为最大度、平均度、最小度时感染程度 图3 起始节点三种不同度在第五个时间步实施三阶双免疫效果

4.1 三阶双免疫策略在初始感染节点为最大度、平均度、最小度的免疫比较

在依据无标度网络特性生成的网路模型中，设定0.4为传播率[3]，从病毒传播时刻开始计时，初始感染节点为最大度、平均度、最小度时感染程度如图2所示，图中横轴为时间步，纵轴为感染节点数.从图中不难看出，度最大的节点染上病毒并传播的速度比度最小的节点、临近平均度的节点传播的都快.

在病毒传播的第五个时间步实施三阶双免疫策略，效果如图3所示.从图3中可以看出，三种不同度节点实施三阶免疫策略达到稳定状态的时间几乎一致.

4.2 三阶双免疫策略与熟人免疫策略、双免疫策略、二阶双免疫策略的效果比较

此次仿真实验传播率和无标度网路同上，在病毒传播达到平衡状态时分别采用免疫策略得出效果如图4所示，横轴为十个时间步，纵轴为前文提到的感染节点数，从图4容易看出，三阶免疫策略优于熟人免疫和双免疫策略.

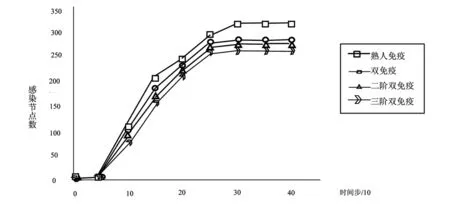
图4 三阶免疫策略与二阶双免疫、双免疫、熟人免疫策略的效果比较

5 结论

无标度网络特性是非均匀网络，许多网络具有这个性质，它们的度分布均符合幂律分布.此研究已经表明无标度网络抗病能力差.本文提出的三阶免疫策略综合了经典的熟人免疫和双免疫[3]的优点，它是对网络中任意抽得的节点中最大度节点及其三阶邻居节点一起实施免疫策略，是对二阶双免疫策略[4]的进一步改进.研究表明,本文提出的免疫策略优于熟人免疫、二阶双免疫，理论上对控制病毒传播具有有效的指导作用，也对此类研究具有一定的参考价值.

[1] 陈端兵，黄晟，尚明生.复杂网络模型及其在疫情传播和控制中的应用研究[J].计算机科学，2011，38(6)：118-121.

[2] 汪小帆，李翔，陈关荣.复杂网络理论及其应用[M].北京：清华大学出版社，2006.

[3] 江静，陈新一.复杂网络上的免疫策略的研究[J].西北民族大学学报，2013，34(4)：30-34.

[4] 刘运节，牟安，陈新一.复杂网络上免疫技术的研究[J].网络天地，2014，17.

[5] 孙婷婷. 复杂网络的病毒传播模型及其免疫策略研究[D].安徽大学，2013.

[6] 何大韧，刘宗华，汪秉宏.复杂系统与复杂网络[M]. 北京：高等教育出版社，2009.

[7] 金伟新. 体系对抗复杂网络建模与仿真[M].北京：电子工业出版社，2010.

[8] 江静. 基于藏文Web的网路模型与免疫策略研究[D]. 西北民族大学，2014.

[9] 徐国锋，刘家保，陆一南，陈中华.复杂网络上的病毒免疫策略研究[J].数学的实践与认识，2012,42(16)：127-131.

[10] Zhou S,Mondragon R J.Accurately modeling the Internet topology[J].Phys.Rev.E,2004,70:066108.

[11] Pastor-Satorras R，Vespignani A． Immunization of complex networks[J].Phys． Rev． E，2001，65: 036134．

[12] Cohen R，Havlin S，Ben-Avraham D． Efficient immunization strategies for computer networks and populations[J].Phys．Rev．Lett．，2003，91: 247901．

2015-05-20

西北民族大学研究生实践创新项目(Yxm2014041).

关风娇(1988——)，女，山东济宁人，硕士研究生，主要从事复杂网络方面的研究.

TP393.08；O157

A

1009-2102(2015)02-0036-04