量子力学中线性谐振子的可视化研究

张 迪，王 丽，姜其畅，苏艳丽

(运城学院 物理与电子工程系，山西 运城 044000)

量子力学中线性谐振子的可视化研究

张 迪，王 丽，姜其畅，苏艳丽

(运城学院 物理与电子工程系，山西 运城 044000)

线性谐振子是量子力学中可以精确求解的一个典型问题。为了直观地理解这一物理模型，借助MATLAB语言分别给出了一维和二维线性谐振子的波函数和概率密度分布图。通过比对理论计算结果和可视化模拟图形，既加深了对线性谐振子问题的理解，又激发了对量子力学的学习兴趣。

线性谐振子；MATLAB语言；可视化

1. 引言

简谐运动广泛存在于自然界中。任何体系在平衡位置附近的小振动(例如，分子的振动、晶格的振动、原子核表面振动以及辐射场的振动等)一般都可以看成是简谐运动即谐振动。对众多实际的谐振动的求解一般是从简化的物理模型即线性谐振子出发，然后再考虑具体的物理情景[1,2]。目前，对一维、二维和三维线性谐振子的理论分析有很多详细的报道[3-5]，但是借助计算机语言对相关理论进行可视化模拟的报道比较少[6]。本文主要借助MATLAB语言，给出了一维和二维线性谐振子的可视化图形，从理论公式和可视化图形两个角度理解谐振子的波函数和概率密度分布的特性。

2. 一维线性谐振子的可视化研究

2.1 在H的本征态下的基本理论

对于一维谐振子，其势能表示为

(1)

则体系的定态薛定谔方程为

(2)

为了便于后面的分析，选择自然单位ћ=μ=ω=1，并令λ=2E则方程(2)简化为

(3)

采用通用的求解方法，将方程(3)的解表示为

(4)

将(4)式代入方程(3)并整理，可得

(5)

方程(5)的解为Hermitian函数即

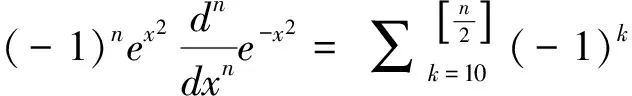
(6)

其中λ应满足λ-1=2n，所以谐振子的能级为

(7)

将(6)带入(4)式可以得到谐振子的波函数为

(8)

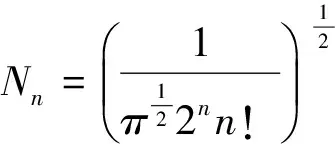
2.2 可视化模拟

在得到一维线性谐振子的波函数表达式(8)的基础上，运用MATLAB语言编写程序绘制不同能级下谐振子的波函数和概率密度分布图像，如图1所示。可以看到：波函数与ψ=0的直线的交点个数为n；概率密度分布满足归一化条件即所包含的面积之和为1。下面以n=2为例，从理论公式和图形特点两个角度来说明上述特点。

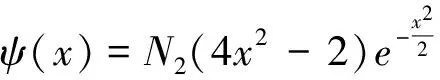
(9)

(10)

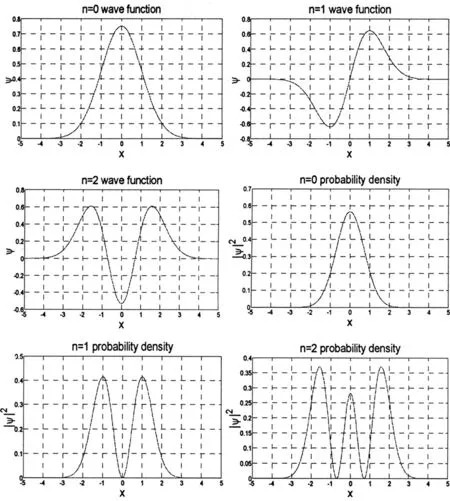
图1 不同能级下一维谐振子的波函数和概率密度分布

3．二维线性谐振子的可视化研究

3.1 在(Hx，Hy)的共同本征态下的情况

关于二维线性谐振子的理论可以分别在直角坐标系和极坐标系中讨论，下面，首先在直角坐标系的情况下，给出谐振子的波函数和能量表达式[2，3]。

体系的定态薛定谔方程为

(11)

同样选择自然单位ћ=μ=ω=1，并令ψ(x，y)=φ(x)φ(y)，借鉴一维谐振子的方法，并注意到二维谐振子在x和y方向上的独立性，最终得到谐振子的波函数

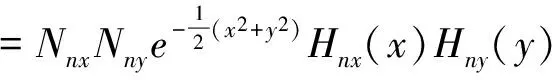
(12)

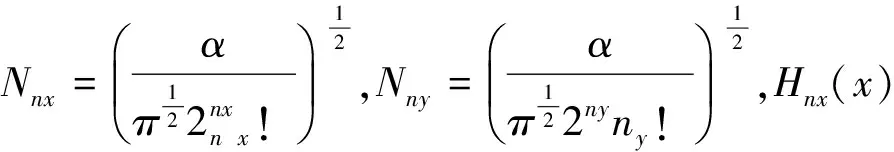
从波函数和能级公式可以清楚的看出二维谐振子的简并度为N+1。当N=0时，相应的基态波函数无简并，其波函数和概率密度分布图像为图2所示。

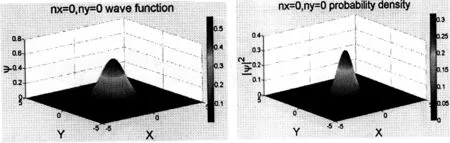
图2 N=0对应的波函数和概率密度图像

同样，当N=1和N=2时，波函数简并度分别为2和3，其波函数和概率密度分布图像分别如图3、4所示。由图2、图3和图4可以看到：波函数与ψ=0平面的交线个数为N；概率密度分布的极大值个数一般为N+1，但是当直角坐标的两个维度的分量都不为零时如nx=ny=1的特殊情况，共有四个极大值。

图3 时波函数和概率密度分布图

图4 时的波函数和概率密度分布图

3.2 在(H，lz)的共同本征态下的情况

下面再从极坐标系的角度分析二维各向同性谐振子的情况。此时，体系的定态薛定谔方程为[5]

(13)

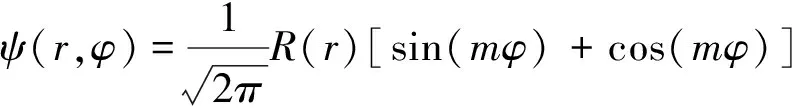
(14)

为了求解方程(14)，首先分析r→0和r→∞两种特殊情况。根据分析结果给出

(15)

将(15)式代入(14)式，得

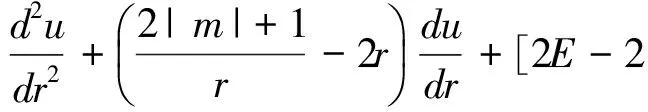
(16)

再令ξ=r2，由(16)式可得

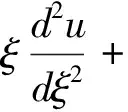
(17)

通过观察可以看出(17)式为合流超几何方程，可以得到其解为

u(r)=F(-nr,|m|+1,r2)

(18)

结合方程(18)和(15)可以得到波函数的表达式

(19)

二维各向同性谐振子的能量本征值为

E=2nr+|m|+1=N+1

(20)

从波函数和能级公式同样可以清楚的看出二维谐振子的简并度为N+1。不同的本征态下的波函数即不同表象下的波函数，应该具有同样的性质。为了说明这一点，我们给出(H,lz)共同本征态下当N=1时的波函数和概率密度分布图。比较图3和图5，可以看到，与直角坐标的情况一样，函数与ψ=0平面的交线个数为1；概率密度分布的极大值个数为2。

4. 总结

本文系统地分析了一维谐振子和不同本征态下二维谐振子的波函数和概率密度分布，并借助MATLAB语言画出了每种情况下的一些能级的波函数和几率密度图像。从这些图像中，我们可以更加形象地理解比较抽象的谐振子问题，而且这些图像的绘制也锻炼了学生的计算机应用能力，激发了学生的学习兴趣。

[1] 邢淑芝，谷开慧，解玉鹏.在恒定弱电场中一维线性谐振子能级的计算[J].吉林化工学院学报，2010(3).

[2] 苟立丹，张志颖，朱瑞晗.二维耦合非线性谐振子的近似求解[J].大学物理，2012(8).

[3] 李嘉亮，张海英.一维及二维线性谐振子的算符解法[J].安庆师范学院学报，2002(4).

[4] 吴英，刘国跃.三维各向同性谐振子基态能量及波函数的两种计算方法[J].绵阳师范学院学报，2007(8).

[5] 梁麦林，王军.在极坐标中求解二维各向同性谐振子[J].大学物理，1999(12).

[6] 陈美华.一维线性谐振子的波函数和几率密度作图方法探讨[J].怀化学院学报，2009(2).

【责任编辑 马太来】

2015-03-11

张迪(1990-)，男，山西运城人，运城学院物理与电子工程系2011级本科生。

O413.1

A

1008-8008(2015)03-0034-03