一种改进的周期长码扩频序列盲估计方法研究*
熊 刚,彭 勃
(中国电子科技集团第三十研究所,四川 成都 610041)
一种改进的周期长码扩频序列盲估计方法研究*
熊 刚,彭 勃
(中国电子科技集团第三十研究所,四川 成都 610041)
提出了一种周期长码DSSS信号扩频序列盲估计改进方法。首先把周期长码DSSS信号建模为虚拟多用户分段系统,周期长码序列可转化为多个都含有模糊矩阵的短码结构;然后采用基于二阶统计量的思路,从矩阵中提取信息去除模糊的影响,并估计得到原始的扩频码序列。通过对该思路的进一步改进,成功应用到多径环境盲估计方法中;最后通过计算机仿真结果验证了该算法的有效性,其性能优于以前的方法。
直接序列扩频 周期长码 盲估计 多径信道
0 引 言
直接序列扩频(DSSS, Direct Sequence Spread-Spectrum)信号在安全保密通信系统、低轨卫星系统、全球定位系统、码分多址CDMA系统等军用和民用领域中都有广泛应用[1]。扩频通信发射机在发送数据之前先采用伪随机(pseudo-noise,PN)序列对基带信号进行调制,直接序列扩频信号的带宽远大于基带带宽,并且信号的功率谱密度通常很低。扩频码序列是直接序列扩频信号重要参数。一般来说,可以分为短码调制扩频和长码调制扩频两种,短码调制是指一个周期的扩频码序列只调制一位信息码;而长码扩频信号的扩频周期大于信息码周期,即一个周期扩频码调制多位信息码。长码调制DSSS信号不仅可以抑制部分符号间干扰,也具有更好的保密性能;另一方面,使得在通信对抗和网络安全监控系统中对DSSS信号进行分析的难度增大。此外,对于多径信道环境和多用户情况,因为信道衰落和多址干扰对信号有较大影响[2],所以这也是扩频码序列盲估计研究中的一个难点。
目前,对于DSSS信号扩频码序列的盲估计,已经提出了一些基于子空间的分析方法,但多数只适用于短码调制,不能直接应用在周期长码DSSS序列盲估计中。为解决上述问题,本文基于将周期长码DSSS信号模型进行转化和二阶统计量的计算优化等思路,提出了一种改进的周期长码扩频序列的盲估计方法,并将该方法扩展到了多径信道环境下。
1 信号模型分析
接收信号的基带模型如图1所示:
如前所述,DSSS周期长码不同于短码,每个周期由多个符号组成。设c(t)表示扩频码序列,扩频序列含G个数据符号,符号持续时间为Ts。设信息码序列{[s(k)]}独立同分布,w(t)表示高斯白噪声。周期长码DSSS信号的表达式如下
(1)
此处cu(t)定义为
(2)
su[k]s[Gk+u-1]u=1,…,G.
(3)
在式(1)中,周期长码DSSS信号与虚拟多用户系统模型是等效的,如图2所示。

图2 周期长码扩频信号等效多用户模型
设第u个用户(u=1,2,…,G)扩频码表示为cu(t),数据速率为1/T。设信号采样周期为T/p。信号的离散形式可表示为
x[n]x(nΔ),c[n]c(nΔ),cu[n]cu(nΔ),w[n]w(nΔ).
(3)
还可表示为信号的过采样形式,如下
(4)

其中
(5)
且
(6)

(9)
其中,设m为整数,且m=p/G。在上式中,C是一个块对角满秩矩阵。下面将利用该特征进行扩频码估计,设信号和噪声序列是零均值的,因此相关矩阵分别为
(10)
(11)

(12)
2 改进的周期长码序列估计方法
将式(12)中的Rx进行特征值分解,可表示为
(13)
其中,U是特征向量矩阵,Λ是特征值矩阵,由此得到:
(14)
上式中,信号子空间的维数是G,因此,信号子空间是由前面的G列特征向量构成的,噪声子空间则由剩余的p-G个特征向量构成。矩阵U即可表示为
(15)
其中,U(s)是代表信号子空间特征向量的矩阵,U(n)是代表噪声特征向量的矩阵。假如信号子空间对应的特征值是各不相同的,则U(s)等价于C。在这里,考虑到Cu在{1,-1}集合中取值以及式 (9)中的码序列结构,则有
‖c1‖=‖c2‖=…‖cn‖
(16)
因此,前面G个特征值是相等的,并且可得出以下关系式
(17)
其中,Q是归一化的模糊矩阵。
对于以前一些方法而言,由于存在模糊矩阵,如果没有先验信息是不可能从二阶统计量(SOS)中估计出C的。但改进后的新方法可以通过等价为各用户短码信号和一些推导运算估计得到周期长码DSSS扩频序列的结果C,算法思路如下。
从式(16)中可得出
C=U(s)Q
(18)

(19)
显然有C1的秩为G-1,即rank(C1)=G-1。因此还可得出
(20)

(21)
因此,qG的表达式为
(22)

(23)
从而可得到
(24)
(25)
因此
(26)

(27)
其中Vj表示特征向量矩阵,Λj表示特征值矩阵。Vj还可表示成
(28)



Qj[qG-j+2,q2,…,qG]
(29)
由于Q是归一化矩阵,故有
(30)
将式(28)代入式(30),可得
(31)

(32)
通过将z代入式(28)并推导,可得到向量qG-j+1。继续采用该思路,还可估计出矩阵Q全部G-1列。为求出Q的第一列,可通过下式得到
(33)
按照这种方法,q1可通过下式得到
(34)

下面分析将该算法应用于多径信道环境。在图3中,可得到一个等效多用户模型。

图3 多径信道周期长码信号等效模型
但与一般的多用户系统不同,各用户占用一个信道且它们都是同步的。因此,该模型类似于CDMA下行链路。由此,信号表达式可表示为
(35)
其中,g(t)是信道的响应,对于各虚拟用户而言都是相同的。设
(36)
其中hu(t)是cu(t)和信道响应g(t)的卷积。目的是为了估计出hu(t),u=1,2,…,G,从而能进行信道均衡同时对扩频信号解扩。考虑到信道响应的持续时间有限,并假设
hu(t)=0,t>(M+1)T,t<0
(37)
信道的离散模型可表示为如下
(38)
还可以简化表示为
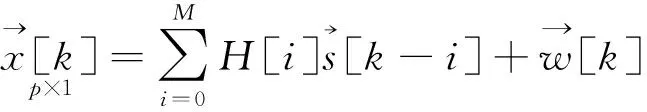
(39)


(40)
为方便,可将接收信号的连续窗看作为一个长为L的块矩阵,并定义下列向量为
(41)
(42)
(43)
通过以上定义式,接收信号中的Lp×1向量可以表示为
(44)
其中ΓL(H)是一个Toeplitz块矩阵,可定义为

(45)

(46)
过去有一些可应用于多径信道的估计算法,例如线性预测的方法等,但它们的性能还需进一步改进[3]。下面引入一种通过矩阵结构特征能够很好实现消除模糊关系和特征值分解的思路,即酉矩阵方法,可以从Rx中估计出Ψ,并去除模糊矩阵Q。该思路首先需构造一个酉矩阵的形式,如下
(47)
其中,Ψ可定义如下
Ψ(H[0]T,H[1]T,…,H[M]T)T
(48)
矩阵Ψ各列是各虚拟用户的扩频码与其共用的多径信道之间的卷积。在这种情况下,根据式(2)和(37),Ψ能表示成如下形式

(49)
其中,符号0m×1表示维数m×1的全零矩阵。
Ψ可表示成如下:
Ψ=[φ1,φ2,…,φG]
(50)
然后可得出如下特征表达式
φu[n]=0 n<(u-1)m,u=1,2,…,G
通过利用矩阵Ψ的特征,可以估计出Q。因此,Ψ也可由下式估计得

(51)
(52)

(53)

(54)

(55)

3 性能仿真和分析
首先对根据前面所述的周期长码DSSS信号虚拟多用户模型推导出的公式(2)~(9)进行仿真,验证算法对周期长码序列的各分段用户扩频码的估计结果。
图4第一行表示原始各分段虚拟用户扩频码序列,图4第二行表示通过本文的改进后的算法得到的结果,该分段序列从图中可以看出估计是正确的。

图4 信噪比0 dB时各分段原始序列及估计结果
下面对多径信道环境中采用本文算法与传统子空间方法进行性能仿真。这里引入序列的互相关系数作为衡量算法估计性能的指标。互相关系数是指两个码序列之间相似性的量度。具体是指算法估计得到的码序列与原始扩频码序列逐比特比较时,一致的数目减去不一致的数目。可用下式表示
(56)
其中,A是估计扩频码序列结果x和原始扩频序列y里面码元相同数目,D是码元不同数目,p是扩频序列码元总数。Rxy数值越大,估计扩频序列准确度越好。图5表示本文算法与传统算法性能仿真曲线。横轴表示信噪比,纵轴表示扩频序列估计结果与原始序列互相关系数,其余参数如前所述。

图5 本文方法与传统方法的性能对比曲线
从上图中可以看出,在信噪比较低的情况下,新算法的性能要优于传统的基于子空间的算法,而且新算法在信噪比为-2dB左右时,估计结果与原始序列的互相关系数为1。
4 结 语
本文利用虚拟多用户分段模型与二阶累积量等思路,提出了一种改进的周期长码扩频序列盲估计方法,并将该算法进一步扩展应用到多径信道环境中。该方法还增强了对噪声抑制能力,通过计算机仿真验证了该算法的性能,在信噪比达到-2 dB以上时可正确进行DSSS信号周期长码扩频序列的估计。今后将进一步优化,为解决低信噪比下DSSS信号扩频序列估计以及盲解扩问题提供一种更有效的手段,也使直接序列扩频通信的监测和对抗技术发展发挥更重要的作用。
[1] 曾璐,谢晓尧. 基于MATLAB扩频通信系统误码率的研究[J].通信技术,2011,44(11):25-29. ZENG Lu, XIE Xiao-yao . Study on Bit Error Rate of Spread Spectrum Communication by MATLAB.[J] Communications Technology. 2011, 44(11):25-29.
[2] J. Ma, “Blind Equalization and Multiuser Detection of DSCDMA signals In Multipath Channel,” Ph.D. dissertation, Auburn University, Alabama, December , 2002.
[3] C. Nsiala Nzeza, R. Gautier, and G. Burel, “Blind synchronization and sequences identification in CDMA transmissions,” in IEEE-AFCEA MILCOM, California, USA, November 2004.
[4] 林智慧,陈绥阳,王元一. m序列及其在通信中的应用[J].现代电子技术,2009,44(08):49-55. LIN Zhi-hui, CHEN Sui-yang. M-Sequence and Its Application in Communication [J].Modern Electrical Technology, 2009, 44(08):49-55.
XIONG Gang(1982.5-), male,M.Sci.,engineer, mainly working at wireless network security and signal processing technology.
彭 勃(1977.8-),男,硕士,高级工程师,研究方向:无线网络安全技术与信号处理技术。
PENG Bo (1977.8—), male, M.Sci.,senior engineer, mainly working at wireless network security and signal processing technology.
A Modified Blind Estimation in PLC DSSS Communications
XIONG Gang, PENG Bo
(No.30 Institute of CETC, Chengdu Sichuan 610041, China)
This paper proposes a method of blind estimation for PLC (Periodic Long Code) DSSS (direct sequence spread spectrum) signal. Firstly, PLC DSSS signal is modeled as a virtual multi-user system,and PLC sequence can be converted to several short-code structures with ambiguity matrix. Then, based on the idea of SOS (second-order statistics), influence of ambiguity matrix is removed and the original spreading codes sequence also estimated.The modified algorithm is successfully applied to blind estimation in multipath environment. Finally, computer simulation verifies the efficiency of this modified algorithm and indicates that its performance is better than that of original one.
DSSS; periodic long-code; blind estimation; multipath channel
S接收信号模型示意图Fig.1 Model of
DSSS signal
10.3969/j.issn.1002-0802.2015.03.006
2014-09-10;
2014-12-25 Received date:2014-09-10;Revised date:2014-12-25
TN918.91
A
1002-0802(2015)03-0272-06

熊 刚(1982.5-),男,硕士,工程师,主要研究方向:无线网络安全技术与信号处理技术;

