一种基于马氏距离的冲突证据组合方法*

鲁 睿，徐启建，张 杰，徐勇军，姚 清

(1.解放军理工大学 通信工程学院，江苏 南京 210007；2.中国电子设备系统工程公司研究所，北京 100141；3.中科院计算技术研究所，北京 100080；4.中国电子设备系统工程公司，北京 100091)

一种基于马氏距离的冲突证据组合方法*

鲁 睿1，徐启建2，张 杰2，徐勇军3，姚 清4

(1.解放军理工大学 通信工程学院，江苏 南京 210007；2.中国电子设备系统工程公司研究所，北京 100141；3.中科院计算技术研究所，北京 100080；4.中国电子设备系统工程公司，北京 100091)

D-S证据理论是高层数据融合中一种重要的处理不确定性问题的方法。但在使用D-S证据理论处理高冲突信息时，经常得出与直觉相悖的结论。证据理论不能有效处理高冲突证据的特点极大制约了其应用，当前研究主要对原始证据源进行修改。提出了一种基于马氏距离确权的组合方法，通过合理度量冲突大小，对原始证据源进行加权修正。经过数值分析，新的组合方法在应对敌对干扰等突发高冲突时性能得到明显改进。

证据理论 证据冲突 马氏距离

0 引 言

证据理论[1](D-S理论)是一种基于统计的数据融合分类算法，可在没有先验信息的情况下实现数据融合，能够比贝叶斯分类算法更有效地表示和处理不确定信息，现已广泛应用于目标识别、数据融合和决策分析等相关领域。

然而在现有证据发生高度冲突时，证据理论会产生与常理相悖的结论，尤其是在军事应用领域，由于战场环境恶劣加之存在敌对干扰，传感器报告信息往往存在着很大的冲突，例如在海洋战场环境中，由于洋流影响、温盐度差异和敌对干扰，同一时刻不同位置的传感器报告经常出现高度冲突甚至相反的现象，使得证据理论的使用面临很多限制。尤其是随着多传感器数据融合[2]的深入研究，这一问题显得愈加突出。

为解决这一问题，国内外研究人员针对证据理论提出了各种改进方法[3]，综合起来主要包括三大类：一是对经典证据理论的模型框架进行修改；二是对经典证据冲突系数K进行重新分配；三是对原始证据源数据进行特定修正。本文采用Mahalanobis距离对证据冲突进行度量，并以此对冲突数据进行修正，经数值分析验证效果较好。

1 D-S理论及其局限性

1.1 D-S理论

在D-S理论[4]中，由变量a的所有原始子命题所组成的命题集U称为a的识别框架，用Θ来表示。

对多个相互独立的可靠命题，经典D-S组合规则为

(1)

1.2 D-S理论的局限性

D-S理论的局限性主要有以下三个方面：一是D-S理论使用的前提要求是证据必须相互独立，这一点在日常工程实践上很难完全满足；二是当证据间冲突比较大、部分证据源不可靠或者识别框架不完备时，D-S组合规则得到的结果可能会有悖于直观判断；三是当识别框架中元素较多时，计算上存在着潜在的组合爆炸问题。其中如何处理冲突证据成为当前D-S理论发展中的一大研究方向。

例1：设有两个传感器对同一物体进行识别，认为可能是A、B、C中的一种。两个传感器的报告表示为：

传感器1：m1(A)=0.99,m1(C)=0.01；

传感器2：m2(B)=0.99,m2(C)=0.01。

即两个传感器都认为是C的可能性最低，但分别认为是其它两种之一的可能性很高。依据D-S组合规则有如下结果：

K=0.999 9，m(A)=0，m(B)=0，m(C)=1，据此得出的结论是C，明显与实际相悖。

2 证据冲突的典型处理方式

2.1 Yager方式及其扩展

(2)

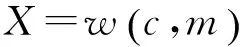
2.2 Murphy方式及其扩展

Murphy[8]首先将n条基本概率赋值进行算术平均，然后用算术平均后的证据来代替原有n条证据，再利用D-S组合规则组合这n条证据

(3)

(4)

(5)

但是对于两个独立的证据进行简单的算术平均是不合理的，丧失了证据推理的许多性能，使组合后的信任度上升，不确定性减小，信息量降低。后人改进了Murphy方式，根据一定的准则进行加权平均，为每一条证据分配不同的权重(即可信度)，从而具有更强的抗干扰能力，收敛速度更快。但是当证据源数目有限的时候，采用Murphy方式决策风险较大，融合结果的可靠性难以保证。

2.3 基于证据距离确权的方式及其扩展

针对证据冲突大时冲突系数K不能很好度量冲突大小这一问题，Jousselme首次提出证据距离[9]这个概念用来代替冲突系数K，在处理冲突数据时取得了较好效果，很多学者在此基础上进行了深入研究和分析对比[10-13]，采用证据距离与其他手段联合的方式对其进行了扩展。

定义2：两条证据之间的Jousselme证据距离为

(6)

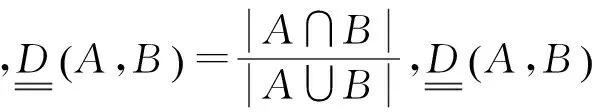
采用基于证据距离确权的方式，利用证据距离的大小来衡量冲突大小，并进行权重分配[14]，在一定条件下合成结果更符合实际。

3 基于马氏距离确权的冲突处理方法

本文利用基于距离的方式修改原始证据源的思想，提出了一种基于马氏距离确权的证据冲突处理方法。

3.1 基本思想

马氏距离(Mahalanobis distance)是由印度统计学家Mahalanobis提出的，表示数据的协方差距离。它是一种有效的计算两个未知样本相似度的方法。它考虑到各种特性之间的联系并且独立于测量尺度。本文使用马氏距离来衡量证据间的冲突度，并构造证据间的支持度矩阵，从而获得各证据在融合过程中的权重，然后根据权重系数对所收集的原始证据源进行加权，最后利用D-S组合规则进行数据融合。其中关键步骤就是如何基于马氏距离计算权重系数。

3.2 基于马氏距离确权的方法

定义3：对于原始证据源mi、mj，它们二者之间的马氏距离为

(7)

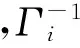
具体步骤：

2)根据下述公式将马氏距离转化为各证据之间的支持度，并构造一个n×n方阵

(8)

(9)

3)根据方阵得出第i个证据获得全部证据的总支持度

(10)

4)对总支持度进行归一化可得第i个证据的可信度

(11)

(12)

7)使用D-S组合规则对加权平均后的证据进行融合。

4 数值分析

下面通过与经典D-S方法、Murphy方法和基于证据距离的方法进行对比来说明基于马氏距离的方法在应对突发高冲突情况下证据融合的有效性。

传感器1：m1(A)=0.5,m1(B)=0.2,m1(C)=0.3；

传感器2：m2(A)=0.5,m2(B)=0.2,m2(C)=0.3；

传感器3：m3(A)=0,m3(B)=0.7,m3(C)=0.3；

传感器4：m4(A)=0.55,m4(B)=0.2,m4(C)=0.25；

传感器5：m5(A)=0.5,m5(B)=0.3,m5(C)=0.2。

分析传感器报告可知，传感器1，2，4，5报告的最大支持目标均为A，但由于传感器自身故障或者突发干扰等原因传感器3报告的最大支持目标为B，通过直观认知，传感器1，2，4，5报告之间的冲突较小，可信度较高，所以目标为A的结果是比较合理的。本文采用上述4种方法进行合成，合成结果如表1所示。

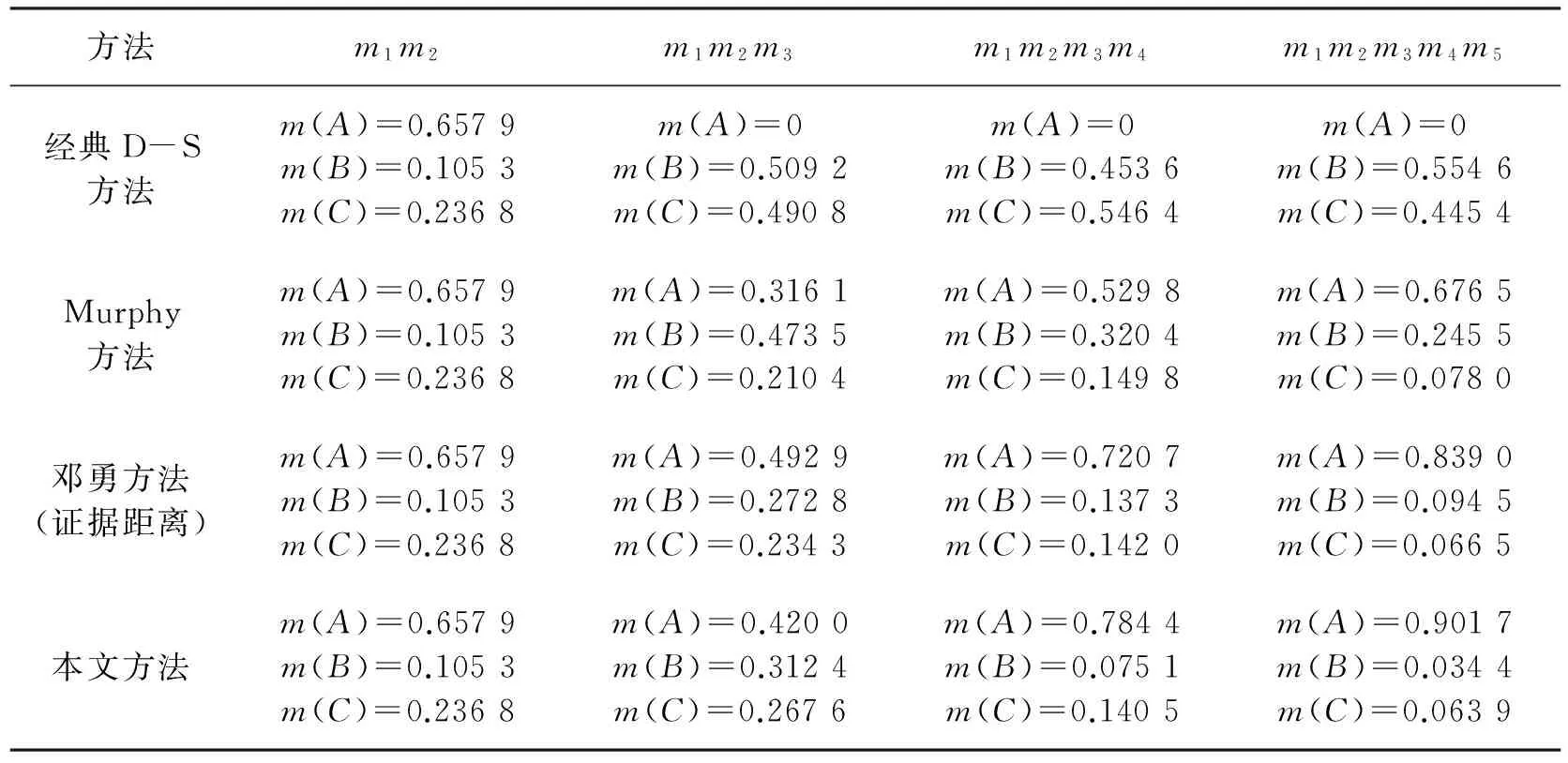
表1 四种证据融合方法结果比较

从表1中可以看出：

1)传感器1和2的报告相同，无论采用哪种方式证据间的距离均为0，合成结果也都相同。

2)传感器3由于自身故障或者突发干扰等原因对其中的A目标判断为0，采用经典D-S方法进行融合时，无论后面传感器4、5报告结果如何，A目标的融合结果始终为0，因此，经典D-S方法无法进行带有含“0”报告的数据融合，在复杂环境或带有敌对干扰时，鲁棒性不强。

3)如果将输出判决门限设定为0.8，则Murphy方法无法正确识别真实目标A。对比后三种方法，Murphy方法仅仅是进行简单的算术平均，没有考虑到证据源之间由于冲突大小不同相应的权重也不应相同。采用算术平均方法，高冲突数据带来的影响往往需要多个低冲突数据来进行弥补，导致收敛速度较慢，数据量较少时无法达到判决门限，无法进行快速反应。

4)本文和基于证据距离确权的方法都能够较快的识别出真实目标，这是由于二者均是通过衡量证据间的冲突程度来引入权重系数，这样就可以很好的削弱高冲突证据对融合结果的影响，提高了收敛速度，在数据量较少时也可以快速达到判决门限，获得正确的融合结果。本文所采用的方法由于对马氏距离采取了取指数运算的处理，在度量过程中放大了高冲突证据间的冲突程度，高冲突证据所获得的权重系数也就相应减小，对融合结果的影响相应减弱，因此本文的方法收敛效果更好。

5 结 语

当遇到恶劣环境导致部分传感器失灵或由于敌对干扰使得个别传感器判断出现反转时，经典D-S理论得出的融合结果往往是不准确的，甚至是反直观的。如何对高冲突证据进行合理度量是数据融合过程中的关键。本文提出了基于马氏距离确权的方法，通过对证据间马氏距离取指数运算来度量冲突大小，对原始证据源进行加权修正后融合，数值分析表明，新的组合方法在应对敌对干扰等突发高冲突时收敛速度更快，收敛效果更好。

[1] Dempster A P. Upper and Lower Probabilities Induced by a Multivalued Mapping[J]. The Annals of Mathematical Statistics,2008,38(2):325-339.

[2] 齐伟, 杨风暴, 周新宇. 一种多传感器数据融合系统方案研究[J]. 通信技术,2010,43(10):84-86. QI Wei， YANG Feng-bao， ZHOU Xin-yu. Study on Scheme of Multi-sensor Data Fusion[J]. Communications Technology,2010,43(10):84-86.

[3] 韩德强, 杨艺, 韩崇昭. DS 证据理论研究进展及相关问题探讨[J]. 控制与决策，2014,29(01):1-11. HAN De-qiang, YANG Yi, HAN Chong-zhao. Advances in DS Evidence Theory and Related Discussions[J]. Control and Decision, 2014, 29(01):1-11.

[4] Shafer G.AMathematical Theory of Evidence[M].Princeton,NJ:Princeton Univ.Press,1976.

[5] Yager R R.A General Approach to the Fusion of Imprecise Information[J].International Journal of Intelligent Systems,1998(12):1-29.

[6] Inagaki T.Interdependence betweenSafety-Control Policy and Multiplesensor Schemes via Dempster-Shafer Theory[J].IEEE Trans.Reliability,1991,40(02):182-188.

[7] 孙全,叶秀清,顾伟康.一种新的基于证据理论的合成公式[J].电子学报,2000,28(08):117-119. SUN Quan, YE Xiu-qing, GU Wei-kang. A New Combination Rules of Evidence Theory[J]. Acta Electronica Sinica, 2000, 28(08):117-119.

[8] Murphy K.CombingBelief Functions When Evidence Conflicts [J]. Decision Suppor Systems, 2000(29):1-9.

[9] Jousselme A L, Grenier D,Bosse E.A New Distance Between Two Bodies of Evidence[J]. Information Fusion, 2001(2):91-101.

[10] 邓勇,施文康.一种改进的证据推理组合规则[J].上海交通大学学报,2003,37(08):1275-1278. DENG Yong, SHI Wen-kang.A Modified Combination Rule of Evidence Theory[J]. Journal of Shanghai Jiao Tong University,2003,37(08):1275-1278.

[11] 刘准钆, 程咏梅, 潘泉等. 基于证据距离和矛盾因子的加权证据合成法[J]. 控制理论与应用, 2009, 26(12): 1439-1442. LIU Zhun-ga, CHENG Yong-mei, PAN Quan, et al.Combination of Weighted Belief Functions based on Evidence Distance and Conflicting Belief[J]. Control Theory & Applications, 2009, 26(12): 1439-1442.

[12] GUNA X, YI X, SUN X M, et al. Efficient Fusion Approach for Conflicting Evidence[J].J Tsinghua Univ (Sci & Tech),2009(49):138-141.

[13] 何友,胡丽芳,关欣等.一种度量广义基本概率赋值冲突的方法[J].中国科学:信息科学,2011,41(08): 989-997. HE You, HU Li-fang, GUAN Xin, et al.A New Method of Measuring the Degree of Conflict Among General Basic Probability Assignments. [J]. Scientia Sinica Informationis, 2011, 41(08): 989-997.

[14] 史超, 程咏梅. 基于证据冲突度的多传感器冲突信息组合方法[J]. 计算机应用研究,2011(03):865-868. SHI Chao, CHENG Yong-mei. Combination Method of Conflict Information from Multi Sensor based on Evidence Conflict Degree[J]. Application Research of Computers, 2011(03):865-868.

LU Rui(1986-)，male，graduate student，majoring in wireless sensor networks.

徐启建(1955—)，男，博士，研究员，主要研究方向为军事通信；

XU Qi-jian(1955-)，male，Ph.D.，research fellow，mainly working at military communications.

张 杰(1974—)，男，博士，高工，主要研究方向为无线传感器网络；

ZHANG Jie(1974-),male, Ph.D., senior engineer, mainly working at wireless sensor networks;

徐勇军(1979—)，男，博士，副研究员，主要研究方向为无线传感器网络；

XU Yong-jun(1979-),male, Ph.D.,associate research fellow, mainly working at wireless sensor networks;

姚 清(1983—)，女，博士，主要研究方向为通信与信息系统。

YAO Qing(1983-)，female，Ph.D., mainly working at communication and information systems.

This paper is supported by Important National Science & Technology Specific Projects under grant(No.2014ZX03006-003)

Combination Method of Conflicting Evidence based on Mahalanobis Distance

LU Rui1， XU Qi-jian2， ZHANG Jie2, XU Yong-jun3， YAO Qing4

(1.College of Communication Engineering, PLA University of Science and Technology, Nanjing Jiangsu 210007, China;2. Institute of Electronic Equipment System Engineering Company, Beijing 100141, China;3. CAS Institute of Computing Technology, Beijing 100080, China;4. China Electronic Equipment System Engineering Company, Beijing 100091, China)

D-S evidence theory is an important method for dealing with uncertainty in high-level data fusion. However, some counterintuitive conclusions are often acquired in handling highly-conflicting informations with D-S evidence theory. Due to this deficiency, the application of evidence theory is severely restricted, thus the current research aims at modifying the original source of evidence. This paper presents a combination method based on Mahalanobis distance, and the original source of evidence is corrected by properly measuring the conflict size.Numerical analysis indicates that, the new combination method enjoys significant performance improvement in dealing with high-conflict situations.

evidence theory; conflicting evidence; Mahalanobis distance

date:2014-11-01；Revised date：2014-02-10

国家科技重大专项(No.2014ZX03006-003)

TP301

A

1002-0802(2015)03-0278-05

鲁 睿(1986—)，男，硕士研究生，主要研究方向为无线传感器网络；

10.3969/j.issn.1002-0802.2015.03.007

2014-11-01；

2014-02-10