一种基于FPGA的简化LLR算法研究*

周小安, 张雅勤，2

(1.深圳大学 信息工程学院，广东 深圳 518000;2.深圳市无线传输与处理技术重点实验室，广东 深圳 518057)

一种基于FPGA的简化LLR算法研究*

周小安1, 张雅勤1，2

(1.深圳大学 信息工程学院，广东 深圳 518000;2.深圳市无线传输与处理技术重点实验室，广东 深圳 518057)

高阶调制方式结合软信息解调的前向纠错编码技术是解决无线通信频谱资源拥挤的有效方法。在传统软信息对数似然比计算方法的基础上，结合mQAM调制技术的正交格雷码映射星座图的特性，提出了一种更简单的计算mQAM软信息方案。在硬件实现上不需要使用乘法器，和传统的LLR计算相比大大节省了FPGA资源，仿真结果表明所提出的LLR简化算法，在(2,1,7)卷积编码下的误码性能接近理想的简化LLR计算结果。

高阶调制 软信息 对数似然比 FPGA

0 引 言

随着现代无线通信系统的发展，4G技术已趋于成熟，这些热门的无线通信技术均以提高通信系统频谱利用率为前提。其中OFDM[1]是一种很好的提高系统频谱利用率的通信系统，在该系统中采用的mQAM[2]调制方式能极大地提高系统频谱利用率，但在发射功率一定的条件下，该多元调制方式在解调时会增加系统的误码率。为了减小系统误码率，通常会在信道编解码时采取相应的措施。有研究表明[3]，在加性高斯白噪声(AWGN)信道中，软判决要比硬判决多2 dB的软判决增益，在衰落信道中软判决增益则超过3 dB。但是对于高阶调制如mQAM，虽然I和Q两路信号独立映射，但是它的每个调制映射符号对应着多个比特，而且必须计算每一个比特的软判决，因此，高阶调制的软信息计算过程较为复杂。文献[4-6]采用格雷映射星座图计算欧式距离而达到简化计算的目的,该方法应用较为广泛。文献[7]采用将复平面分块计算的方法对非方形星座的简化计算进行了研究，在简化计算的同时不影响系统性能。文献[8-9]在OFDM-IM系统中使用LLR计算或ML检测，其系统性能更优于传统OFDM系统。

本文对传统软判决简化方法和提出的方案作了算法分析，采用(2,1,7)卷积码以1/2的码元速率对信源进行编码并通过AWGN信道，接着采用Viterbi对计算出的软信息进行解码并分别计算误码率，在16QAM软信息计算的基础上，扩展至64QAM软信息计算，并对这些方法进行了软硬件仿真。仿真结果表明，本文提出方案的软信息解码性能接近理想的简化LLR计算结果。

1 传统计算软信息方法

传统的软判决算法是一种基于最大后验概率准则的对数似然比计算方式，且软解调输出与硬解调输出具有相同的符号。以16QAM为例，正交幅度调制(QAM)是利用多进制振幅键控和正交载波调制相结合产生的，16QAM即是一种振幅相位联合键控信号，其星座图采用正交格雷映射方式，如图1所示。将16QAM信号映射到星座点后，每个映射符号均可以用4个比特的向量(a1,a2,a3,a4)来表示，其中a1,a2,a3,a4均在0和1中取值。设前两比特在集合bI,k中，映射为同相分量，后两比特在集合bQ,k中，映射为正交分量，其中k=0,1。设星座图中任意一点的坐标为(AI,AQ)，经过高斯白噪声信道后接收到的信号为r=a+w=rI+jrQ，其中rI=aI+wI，rQ=aQ+wQ，a为接收到的信号，w为方差为σ2的高斯白噪声，其同相分量rI,及正交分量rQ可以看成是两组相互独立的随机变量。r的条件概率密度函数为[10]

(1)

式中，A=AI+jAQ。

图1 16QAM星座图

传统LLR计算方法对数似然比(Log Likelihood Ratio)函数的定义[11]为

(2)

设信源等概率分布，根据Bayes准则可得

(3)

由式log∑iri≈maxilogri,得

(4)

化简后可得

(5)

根据I、Q两路信号的独立性

(6)

由式(5)、式(6)可知，传统简化LLR算法计算16QAM步骤为：

第1步，将数据映射到16QAM星座图，得到16QAM调制数据。

第3步，由式(5)即可得第一比特的最小对数似然比LLR(bI,1)。

2 本文提出的LLR计算方案及性能仿真

(7)

(8)

式中，K=1/2σ2，a为调制星座图的单位幅度。根据log∑iri≈maxilogri得，16QAM调制信号I路第一比特a1的LLR计算公式可以表示为

LLR=min{(rI-3a)2,(rI-a)2}- min{(rI+3a)2,(rI+a)2}

(9)

令

针对16QAM调制信号，根据其正交格雷码映射的星座图特性及d0与d1的关系，I路信号第一比特a1的LLR计算公式为

(10)

(11)

同理，其I路信号第二比特a2的LLR计算公式为

(12)

(13)

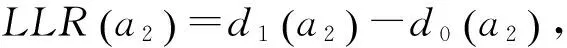
Q路信号第三比特a3的LLR计算公式(与a1对称)为

(14)

(15)

Q路信号第四比特a4的LLR计算公式(与a2对称)为

(16)

(17)

64QAM调制的星座图如图2所示，映射符号所表示的前3比特为I路调制信号，后3比特为Q路调制信号。从星座图可以看出，其LLR计算的边界值为±6、±4、±2和0，计算公式与16QAM类似。由此可见，本文提出的方案计算LLR只需要先判断该映射点落在星座图中的位置，然后由该位置来分别计算其到硬判为1和硬判为0的星座点的距离，并且对I路信号只需计算横向距离，对Q路信号只需计算纵向距离，最后计算两者距离的差值即可得到该映射点的LLR。在本文方案中，每个16QAM符号(每个符号需要计算4个LLR)计算LLR需要4×2=8次比较和4×3=12次加、减法；传统简化LLR算法计算16QAM需要2×16=32次乘法(距离的平方：横向距离的平方+纵向距离的平方), 16次加、减法以及4×7×2=56次比较。本文提出的方案采用边界比较的方式，避免了乘法计算并明显减少了比较次数，可大大降低计算复杂度，提高计算效率。

图2 64QAM星座图

本文仿真过程如下，先将信号经过16QAM或者64QAM调制后进行(2,1,7)卷积码编码，经过AWGN信道，然后分别采用传统简化方法和本文提出方案分别计算它们的LLR，最后将得到的LLR通过Viterbi译码并绘出了误码率(Ber-Eb/N0)仿真曲线[12]。以下是未经编码得到的硬判决解调结果(UncodedHard)与利用传统方法(LLR1)、本文提出方案(LLR2)及硬判决(Hard)结果解调得到的误码率仿真结果,如图3、图4所示。从结果可以看出在相同的误码率情况下，简化软解调比未经编码的硬解调对信噪比的要求低6～7dB；对16QAM和64QAM调制系统而言，本文提出的方案实现简单而且解调效果接近理想的简化LLR解调性能。

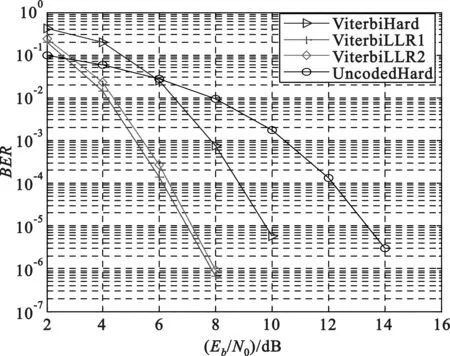
图3 16QAM四种算法解调性能曲线

图4 64QAM四种算法解调性能曲线

3 LLR计算的FPGA硬件实现

为了进一步验证本文提出的简化LLR计算方法的硬件可实行性，根据2中的算法，在FPGA中编写Verilog代码，利用Modelsim进行时序仿真，并与硬判决输出的数值符号相对比(本文采用127代表正数，-128代表负数)，仿真结果如图5所示。最后把硬件FPGA输出的LLR结果保存至文件，并与Matlab仿真输出的文件相比较，通过Matlab对二者的结果进行比较发现，软硬件计算的LLR2完全相同，仿真结果如图6、图7所示。

将数据对比分析可知，本文提出方案的硬件仿真结果与传统简化计算的变化趋势、数据符号完全一致，只是硬件结果数值大小上有所不同，图6和图7中两种方法的软硬件结果比较完全一致，充分说明了本文提出方案的硬件可行性，图3和图4表明采用这些数值的解调性能与传统简化算法相比略有差别。

图5 本文LLR算法的Modelsim仿真结果

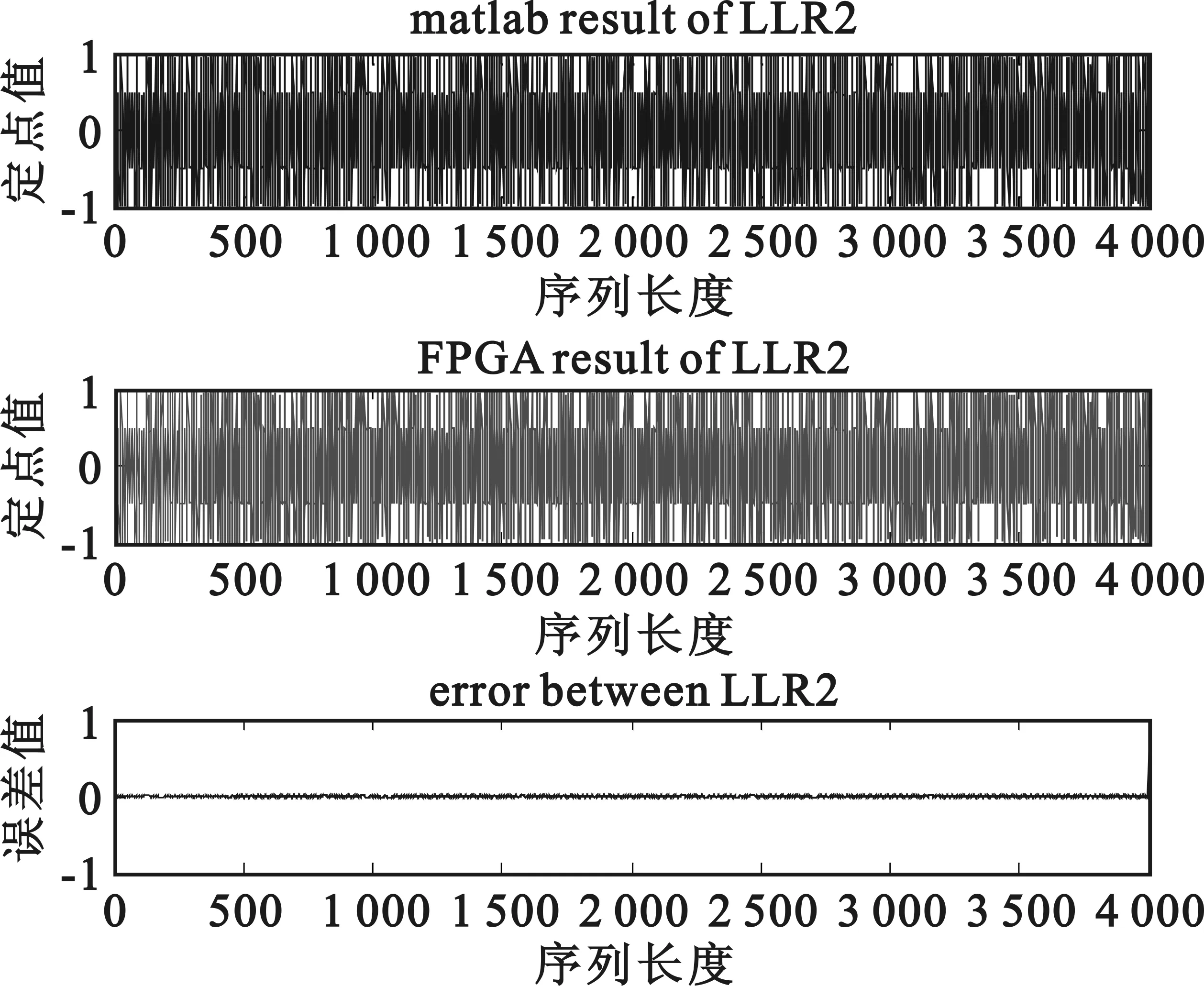
图6 16QAM软硬件输出LLR2结果对比

图7 64QAM软硬件输出LLR2结果对比

将传统简化方法与本文提出方案的工程在Xilinx型号为XC4VLX100的一颗FPGA上综合实现。以64QAM的LLR硬件实现为例，其硬件FPGA资源使用情况如表1所示。

表1 FPGA资源使用情况

另外，若不使用硬件资源提供的IPCore实现乘法器功能，则传统简化算法计算64QAM的LLR需要使用128个乘法器资源。

4 结 语

本文首先通过分析传统软信息计算方法和本文提出方案的软信息计算方法，在此基础上结合前向纠错编码(FEC)[8-9]mQAM调制技术的正交格雷码映射星座图的特点，提出了一种更简单的计算mQAM软信息方案。然后以(2,1,7)卷积编码为例，通过matlab仿真，对比了两种方法在16QAM和64QAM调制系统中的误码性能[7]。最后通过FPGA仿真验证了本文方案的可行性，并对两种方案实现所占用的FPGA资源作了比较，由于本文方案算法简单，不需要使用乘法器，大大节省了FPGA硬件资源。总体来说，本文提出的LLR计算方案，以略微的性能代价换取了LLR算法复杂度的降低，计算更简单，更易于硬件实现，具有一定的参考和应用价值。

[1] 屈兰，张德民，谢显中.2种简化的LDPC译码算法在OFDM系统应用中的改进[J].重庆邮电大学学报：自然科学版，2007,19(02):154-158. QU Lan, ZHANG De-min, XIE Xian-zhong.Improvement of Two LDPC Decoding Algorithms as Applying in the OFDM system[J].Journal of Chongqing University of Post and Telecommunications (Natural Science).2007,19(02):154-158.

[2] 赵晋，张建秋.快速生成QAM比特置信度软判决度量的算法[J].电子信息学报，2009,3(04)：985-988. ZHAO Jin, ZHANG Jian-qiu. Bit Confidence Based Soft Decision Metric Generation for QAM[J].Journal of Electronics &Information Technology,2009,3(04)：985-988.

[3] Stephane LG, Glavieus A, Claude B. Turbocodes and High Spectral Efficiency Modulation[C].Proceeding of ICC 1994,41(02):645-649.

[4] 闫涛，茹乐，杜兴民.一种基于折线逼近的对数似然比简化算法[J].电子与信息学报，2008,30(08)：1832-1835. YAN Tao, Ru Le, DU Xing-min. A simplified Log-Likelihood Ratio Algorithm with Broken Line Analysis[J].Journal of Electronics & Information Technology.2008,30(08):1832-1835.

[5] 王晓晴，杨知行，彭克武等.一种M-QAM软判决解映射的简化算法研究[J].电视技术，2008(01): 17-19. WANG Xiao-qing, YANG Zhi-xing, PENG Ke-wu. Research of Simplified Soft-Output Dema-pping Algorithm for M-QAM[J].Digital TV.2008(1):17-19.

[6] 卢海风，陈伟，黄秋元.一种应用于OFDM通信系统的简化软判决算法[J].武汉理工大学学报：交通科学与工程版，2009,33(01):114-120. LU Hai-feng, CHEN Wei, HUANG Qiu-yuan. A Simplified Soft Decision Applied to OFDM communication System[J].Journal of Wuhan University of Technology(Transportation Science & Engineering).2009,33(01):114-120.

[7] 王磊，徐大专.32QAM比特信息简化计算[J].应用科学学报，2010，28(04):331-336. WANG Lei, XU Da-zhuan. Simplification of Bit Metric Calculation for 32QAM[J]. Journal of Applied Sciences Electronics and Information Engineering.2010,28(04):331-336.

[8] Orthogonal Frequency Division Multiplexing with Index Modulation in the Presence of High Mobility.[C]2013 First Internati-onal Black Sea Conference on Communicati-Ons and Networking.2013,3(5):147-151.

[9] A Design of Low Complex Log Likelihood Ratio for MIMO Decoder Using the Bit Shift[J] .IEEE Circuits and Systems.2014,17(20):717-730.

[10] Filippo Tosato, Paola Bisaglia. Simplified Soft-Output Demapper for Binary Interleaved COFDM with Application to HIPERLAN/2[J].IEEE conference publications,2002,33(08):664-668.

[11] Fagervik K, Jeans T G. Low Complexity Bit Soft Output Demodulator[J].IEEE Electronics Letters,1996,32(11):985-987.

[12] 梁尧，周明宇，何丽.二维MMSE信道估计算法研究与FPGA实现 [J].通信技术2014,47(11):1249-1254. LIANG Yao, ZHOU Ming-yu, HE Li. 2D MMSE Channel Estimation Algorithm and FPGA Implementation[J].Communications Technol Ogy，2014，47(11):1249-1254.

ZHOU Xiao-an(1968-)，male ,Ph.D. , associate professor, majoring in nonlinear circuit system theory.

张雅勤(1990—)，女，硕士研究生，主要研究方向为无线通信及其FPGA实现。

ZHANG Ya-qin(1990-)，female, graduate student, majoring in wireless communication and FPGA hardware development.

A Simplified LLR Algorithm based on FPGA Implementation

ZHOU Xiao-an1, ZHANG Ya-qin1,2

(1.College of Information Engineering , Shenzhen University , Shenzhen Guangdong 518000,China;2.Shenzhen KeyLaboratory of Wireless Broadband Communication and Singal Processing,Shenzhen Guangdong 518057,China)

Combination of high-order modulation with FEC (Forward Error Correction) coding in soft information of demodulation is an effective solution to crowded wireless communication spectrum resources. Based on traditional log likelihood ratio soft information calculation method, and in combination with the feature of mQAM constellation for its orthogonal Gray code mapping, a fairly simple scheme for calculating soft information for mQAM is proposed. This scheme requires no hardware multipliers, and thus could save considerable FPGA sources compared with traditional LLR calculation. Simulation results indicate that the simplified LLR algorithm is quite close to the ideal traditional LLR algorithm in BER performance with (2,1,7) convolutional coding.

mQAM; soft information; LLR;FPGA

date:2014-11-08；Revised date：2015-02-10

TN918

A

1002-0802(2015)03-0262-05

周小安(1968—)，男，博士，副教授，主要研究方向为非线性电路系统理论；

10.3969/j.issn.1002-0802.2015.03.004

2014-11-08；

2015-02-10